量子氣體中的輸運行為*

張世忠

(香港大學物理系,理論和計算物理中心,香港)

輸運測量是了解物質性質的一個重要手段.本文簡單介紹最近在量子氣體中實現的輸運實驗及其主要結論,包括在類似于介觀物理器件中的Landauer輸運和強相互作用費米氣體中的自旋輸運行為.我們著重討論自旋動力學的特殊性以及其由于全同粒子相互作用所導致的特殊自旋擴散流的形式.

1 引 言

最近幾年來,輸運行為成為量子氣體研究中的一個主要方向.這些研究主要集中在以下幾個方面.首先是一般集體運動中的弛豫行為,比如說在諧振子勢中呼吸模式的衰變和體積黏度的關系[1].這類實驗關心的是體系的集體激發,測量的物理量一般是在勢阱中密度平均之后的結果,因此其物理解釋需要比較多的模擬.其次是類似于傳統固體物理實驗中的輸運,比如說在磁勢阱或者光晶格中電導以及自旋擴散的研究[2?9].量子氣體的一個突出優點是它具有比較高的可控性和可調制性.實驗中可以較容易地改變體系的相互作用,維度等等.尤其重要的是,利用光學控制,人們可以在比體系本征時間尺度更短的時間內調節體系的參數,從而為研究驟變現象提供了一個很好的平臺.

2 量子氣體的特殊性

相比于傳統的凝聚態(包括電子氣,液氦等),量子氣體這種比較新的多體量子系統具有其特有的性質,從而也導致了一些特有的現象和問題[10?12].

在量子氣體的研究中,我們一般關心的是處在電子構型基態上的堿金屬原子,比如鈉(Na)或者鉀(K).這些原子之間的相互作用是由一個長程的范德瓦耳斯吸引勢和一個強烈的短程排斥勢所構成,如圖 1.C6是范德瓦耳斯常數.對于這樣的兩體相互作用而言,我們可以定義一個特征長度,范德瓦耳斯長度r0,其大小可以通過平衡兩體動能和相互作用能的大小來得到[9,10]

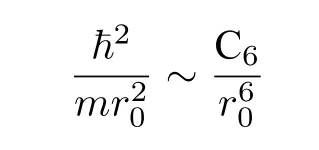
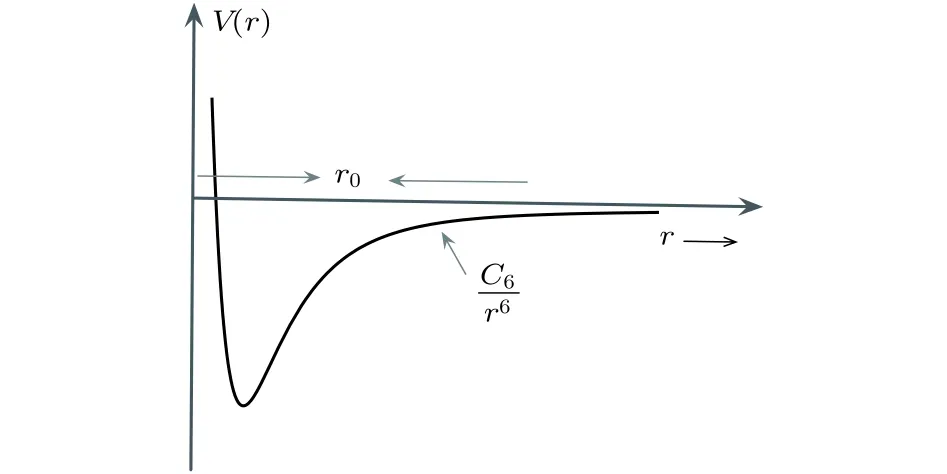
圖1 原子之間的范德瓦耳斯吸引勢和短程排斥勢Fig.1.van der Waals attractive potential and short-range repulsive potential between atoms.

表1 冷原子物理研究中的三個不同區域Table1. Three different regimes in the study of cold atom physics.

在光晶格中,相鄰格點之間的距離dL提供了一個新的長度尺度[16].對于現有的實驗而言,一般.另外,單個光晶格可以近似為一個簡諧振子勢,其中.V0是光場勢的幅度,是反沖能量.k 是光晶格相干激光的波矢.實驗上可以通過控制V0的大小來控制單個光晶格勢束縛的強弱.我們可以定義諧振子長度.一般而言,其對應的能量尺度給出光晶格中能帶之間能隙的大小.如果,我們可以忽略激發能帶的貢獻.

在考慮非平衡態輸運的時候,一個比較重要的問題是如何處理和描述粒子之間的相互作用.在平衡態,我們所關心的物理量不隨時間變化,多體波函數在空間的分布以及關聯也不隨時間變化.在這種情況下,復雜的相互作用勢可以由低能散射的幾個參數來描述.具體而言,對于s-波散射的問題,兩體相互作用可以寫成[9,17]

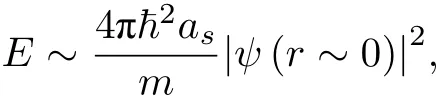
3 量子氣體中的輸運實驗

本文著重討論類似于固體物理中的輸運實驗.我們大概可以將這類輸運實驗分成兩類.一類實驗關注類似于介觀量子結構的特殊勢場構型的輸運行為.另一類實驗注重于測量束縛在諧振子勢場或者盒子勢中的量子氣體的輸運系數.首先簡單介紹前一類實驗(詳細介紹可參考文獻[2]),之后再討論后一類實驗.

3.1 類似于介觀物理器件的輸運實驗[2]

在這類實驗中,玻色子或費米子被束縛在一個各向異性的諧振子勢中.諧振子勢的頻率滿足如下條件:.沿著 y 方向,一束藍失諧的激光將原子團沿著x方向分成三部分:兩側未經擾動的原子和中間的準二維區域.一般而言,原子團在x方向的大小約為300微米,而準二維區域在x方向的大小約為50—60微米.沿著垂直于準二維區域的z方向上,諧振子頻率可以達到3.9kHz.注意到準二維束縛區域的大小比起原子氣體的所有特征長度都大.在這個范圍內,束縛勢導致的空間運動量子效果可以忽略,體系處于多通道區域.在進行類似電導輸運實驗的測量中,可以調節兩側原子的相對數目()來產生兩側化學勢差:

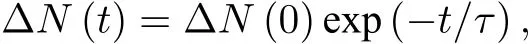
同樣在多通道區域,實驗上可以通過再加上一個高斯激光束來調節在二維區域內的原子密度.由于在有吸引相互作用的費米系統中存在超流,這類調控顯得更為重要.在保持溫度不變的情況下,如果二維區域的原子密度比較低,體系處于正常態,實驗上發現依舊滿足指數形式衰減;當密度變大到使得體系處于超流狀態時候,的長時行為不再滿足指數衰減形式,反而呈現出殘余震蕩的跡象.另外的短時指數衰減行為被解釋成由于渦旋的產生所導致的超流衰變,但是這還有待于進一步的研究.

在多通道實驗設置的基礎上,加上另一藍失諧的激光系統,可以在原先二維區域制造出一個更窄的區域(量子點接觸),大概5.5微米沿著x方向;沿著垂直方向的束縛非常強,有效的諧振子頻率最高可達KHz,尺度大約 1.5 微米.在這種情況下,我們需要計入徑向的量子化的后果.由于輸運處于單個或少數幾個通道的區域.通過改變的大小,實驗上可以調節有效通道的數目.對于無相互作用或者弱相互作用費米系統,彈道輸運給出量子化的電導G=n/h,n是費米面下的通道數目,h是普朗克常數.這在實驗上被驗證了.

對于強相互作用的費米系統而言,單通道下的輸運表現出更有趣的性質.在超流態,實驗上觀察到約瑟夫森動力學過程以及多次安德烈夫反射導致的正常粒子流.在靠近超流溫度的正常態以及較高溫下,實驗上測量到的電導隨著的改變仍然表現出量子化的結構,但是量子化的值不再是之前的 n/h 的形式,而是,是一個依賴于溫度以及相互作用的常數(不一定是整數).一類的理論解釋認為這是在強相互作用下超流溫度附近的漲落效應導致的[18,19];另一類解釋認為在量子點接觸處的強束縛導致原子密度較高,從而該處處于超流態.因為兩邊的量子氣體仍舊在正常態,所以邊界處的安德烈夫反射導致電導加強[20].

3.2 量子氣體中的自旋擴散實驗

下面著重討論第二類輸運實驗.解釋這類實驗的一個復雜之處在于實驗中的原子是被束縛在諧振子勢中,所以一般情況下輸運行為和諧振子勢中的動力學過程是耦合在一起的.區分內秉的輸運行為和諧振子勢中的集體行為通常不是那么容易.在下面的討論中,假設實驗上的這些麻煩可以被適當的處理,而只討論由于強相互作用而導致的內秉的輸運行為.作為一個例子,我們將討論強相互作用的費米系統中的自旋擴散行為[7?9].關于強相互作用費米子體系粘滯系數的行為請參見文獻[21,22].

我們首先討論二元流體中的擴散.假設體系中有兩種原子,這兩種原子的總質量分別為M1和M2,密度分別為和,速度分別為和.如果,擴散現象就會發生.設想一體積元,其質心運動速度為.對于單純擴散行為,在質心系中兩種原子的流密度可以寫成.然而,宏觀的觀察告訴我們,擴散流密度的大小和密度的梯度成正比關系:

我們注意到對于縱向自旋流而言,它在自旋空間的方向和自旋密度是一致的,而在空間的方向則由自旋密度大小的梯度來決定.對橫向的自旋擴散而言,事情就比較復雜了.我們首先注意到在自旋空間,橫向自旋流和自旋密度方向是垂直的.這決定了在自旋空間,它可能的方向是或者

.具體計算發現[23],其中是一個新的參數(Leggett-Rice參數).最初上面的方程是在研究簡并費米液體氦-3中推導出來的.其后的研究發現,這樣的自旋流不僅僅描述簡并費米液體里面的自旋輸運,同時也描述了非簡并量子氣體中的自旋擴散行為(全同自旋旋轉效應[24]).在后面一種情況下,它描述了由于全同粒子交換不變性所導致的自旋進動.具體物理可以由圖2中描述的兩體散射看出來[25].

圖2 全同自旋旋轉效應Fig.2.Identical spin rotation effect.

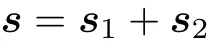
散射過程中,單個自旋會繞著總自旋s作進動.假設在散射過程中,改變,改變.那么.但自旋流因此改變了,

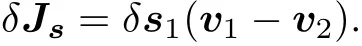
相應的微分散射截面可以寫成

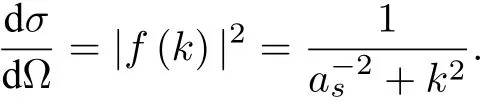
對于一般的擴散過程,玻爾茲曼方程給出如下形式的擴散系數

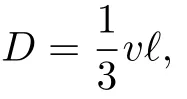
在上式中,v是平均速度.因為上面的討論對縱向和橫向自旋擴散都適用,所以我們先不區分和,而統一寫成 D.在實際推導中,平均速度的定義并不是非常明確,而且上式中的系數也不是很確定的系數.但是擴散系數的量綱以及其隨溫度和相互作用的變化是可以由上面的表達式確定下來[26].考慮在簡并溫度之上,,粒子的平均速度,對于弱相互√作用體系因為自由程不依賴于溫度,所以;在強相互作用下,,所以.在低溫下,我們需要計入由于費米面的存在而導致的散射相空間變小,另外我們也不能使用高溫時的粒子觀念,而應該計入相互作用對粒子的重整化效果(朗道準粒子).最終的結果是;這樣的溫度依賴在低溫朗道液體理論里是非常常見的.常數C在弱相互作用的時候還是和成正比;在強相互作用下,,它就是一個常數.從上面的分析可以看出,D隨溫度的變化是非線性的.高溫以及低溫D都是比較大.在溫度的時候達到最小值.其大小可以由量綱分析得到

有的時候,大家認為由于海森伯不確定原理,D會有一個最小值:,因為自由程不能小于德布羅意波長.但是這類論證依賴于擴散系數的動力學表達式,而在自由程和德布羅意波長相當的時候,針對粒子或者準粒子的玻爾茲曼方程不一定成立,所以不是很有說服力.實驗上的確發現在散射共振附近,擴散系數達到一個最小值,見表2.我們注意到二維縱向自旋擴散還沒有被測量,另外實驗給出的二維橫向自旋擴散也存在相互矛盾,這還有待進一步實驗研究.

表2強相互作用費米系統的自旋擴散系數Table2. Spin diffusion constants for strongly interacting Fermi gases.

如果需要更加精確地計算擴散系數和Leggett-Rice參數的大小,我們需要考慮碰撞積分的詳細形式.從動力學理論我們可以得到的表達式[27,28]

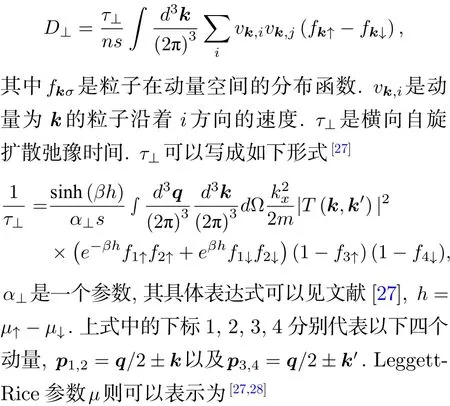
需要指出的是,在散射共振附近的強相互作用費米子體系中,雖然以上計算和實驗大概吻合,但是不代表這些動力學計算已經抓住了本質的物理.這主要有以下原因.第一,對于描述體系的自旋動力學的方程而言,它的形式在很大程度上已經由對稱以及守恒律決定了,不依賴于動力方程的推導過程.第二,玻爾茲曼方程的出發點是體系有比較好的準粒子,但這對于處在共振附近的正常費米體系來說還是一個沒有完全解決的問題.利用全像原理 (holographic principle),我們可以對一些無正常準粒子的體系進行一些初步可控的輸運計算[29].

4 結 論

作為總結,我們想提一下最近在光晶格中的原子輸運和自旋輸運實驗[3?5].這一類實驗的主要目的在于模擬Fermi-Hubbard模型在低溫乃至零溫下的性質.這些冷原子模擬實驗中的溫度還沒有達到超交換相互作用的尺度,因此輸運行為可以認為是相對高溫下Fermi-Hubbard模型的行為.一個比較值得關注的發現是在低參雜時出現類似于高溫超導中電導和溫度的線性關系[4],另一個是在高參雜的時候電導在強相互作用下的飽和行為[3].在冷原子體系,這方面的探索現在才剛剛開始,我們期待之后更多的實驗和理論發現.