基于卡爾曼濾波的汽輪機參數估計應用

毛朋濤

摘要：針對火力發電中汽輪機健康參數估計問題，研究了一種非線性卡爾曼濾波估計方法，比較了擴展卡爾曼濾波（EKF）和無味卡爾曼濾波（UKF）兩種方法對參數估計效果，最終本文選取EKF對實際運動軌跡和期望運動軌跡進行研究。結果表明：擴展卡爾曼濾波能夠很好地對參數進行估計，是一種實用的非線性參數估計方法。

關鍵詞：卡爾曼濾波;汽輪機;參數估計

中圖分類號：TP311? ? ? 文獻標識碼：A? ? ? 文章編號：1009-3044（2019）02-0254-02

1 引言

汽輪機性能參數估計作為火力發電健康管理系統重要內容，為其健康評估、維修計劃制定提供依據，當前對汽輪機故障診斷采用的技術主要為：基于模型診斷、基于信號處理、基于專家知識庫和基于機器學習的，其中基于模型診斷技術通過診斷邏輯實現故障判斷和預測，廣泛應用于汽輪機的健康管理中[1-2]。

在參數估計當中，很難找到一種嚴格的遞推濾波算法，通常用近似方法去解決非線性濾波的問題。一類方法是尋找非線性函數的線性近似，線性化非線性模型：通過泰勒展開近似得到了擴展爾曼濾波（EKF），通過插值多項式近似得到了差分濾波（DDF）[3]。另一類方法是基于近似非線性函數的概率分布比近似其函數本身更容易的思想，通過UT 變換選擇一組確定的點集來表征狀態的統計特性（如均值和方差等），能直接應用非線性模型來求解，即無味卡爾曼濾波（UKF）[4]。后者計算較長，實時性較差，為此本文選擇第一類方法中的擴展卡爾曼濾波方法對汽輪機進行參數估計。

本文選擇擴展卡爾曼濾波并將其應用在汽輪機健康參數估計上，首先，建立汽輪機旋轉運動軌跡模型;其次，運用EKF對模型進行跟蹤仿真，最后給出仿真結果。

2 汽輪機模型

本文所用汽輪機非線性部件級模型，是根據非線性氣動熱力學方程描述對象，利用汽輪機連續、功率平衡建立汽輪機非線性動力學工作方程，實現對其動靜態仿真和期望軌跡的追蹤，某汽輪機在穩定工作點附近的模型為[5]：

[Δxk+1=f（Δxk，Δuk）+wkΔyk=H（Δxk，Δuk）+vk]? ? ? ? ? ? ? ? ? ? ? ?（1）

其中，控制變量[Δu=[Δwf，ΔVS，ΔVB]]，[wf]為汽輪機進氣量，[VB]為可調放氣活門，[VS]為可調間隙，x為反映汽輪機工作狀態變量，包括轉速、部件效率和流量的參數。本文選取的健康參數有高壓氣機效率、流量退化量和能效，因此可得[Δx=[ΔNl，ΔNh，Δη，Δw]];輸出參數[Δyk=[ΔNl，ΔNh，ΔT，ΔP]]，分別為低壓轉速、高壓轉速、高壓氣機進口溫度和高壓氣機出口壓力;[wk，vk]為互不相關高斯白噪聲，其協方差矩陣分別為Q和R。[f（·），H（·）]表示汽輪機工作過程的非線性函數。汽輪機在工作過程中由于腐蝕或者卡滯等因素，都會表現為健康參數突變。

3 基于卡爾曼濾波器的參數設計

3.1 擴展卡爾曼濾波器設計

EKF將非線性系統在狀態估計值附近作泰勒展開，取其一階截斷作為原狀態方程和觀測方程的近似式實現線性化，然后對線性化后的系統采用卡爾曼濾波進行狀態估計。

對于形如式（1）的系統，首先根據上一時刻的狀態估計值[xk-1]及狀態一步預測值[xk|k-1]構造雅克比矩陣[6]：

[Fk|k-1=?f（xk，k）?xk|xk=xk-1=?f1（xk，k）?x1，k…?f1（xk，k）?xn，k????fn（xk，k）?x1，k…?fn（xk，k）?xn，kxk=xk-1]? ? ? ? ? ? ? ? ? ? ?（2）

[Gk=?g（xk，k）?xk|xk=xk-1=?g1（xk，k）?x1，k…?g1（xk，k）?xn，k????gm（xk，k）?x1，k…?gm（xk，k）?xn，kxk=xk-1]? ? ? ? ? ? ? （3）

系統狀態的均值與方差陣一步預測為：

[xk|k-1=f（xk-1，k-1）]? ? ? ? ? ? ? ? ? ? ? （4）

[Pk|k-1=Fk，k-1Pk-1FTk，k-1+Qk-1]? ? ? ? ? ? ? ?（5）

在接收到最新觀測數據[yk]后，對[xk|k-1]和[Pk|k-1]進行修正，分別為：

[xk=xk|k-1+Kk[yk-g（xk|k-1，k）]]? ? ? ? ? ? ? ?（6）

[Pk=1-KkGkKk|k-11-KkGkT+KkRv，kKTk]? ? ?（7）

式中 [Kk]濾波增益矩陣，計算公式為：

[Kk=Pk|k-1GTk[GkPk|k-1GTk+Rv，k]-1]? ? ? ? ? ?（8）

由式（2）～式（8）構成了擴展卡爾曼濾波算法的遞推公式，那么對應于遞推貝葉斯估計算法用擴展卡爾曼遞推算法中的狀態量可以分別表示為：

[p（xk|Yk-1）=N（xk;xk|k-1，Pk|k-1）]? ? ? ? ? ? ?（9）

[p（xk|Yk）=N（xk;xk，Pk）]? ? ? ? ? ? ? ? ? ? （10）

對于算式（1）中，利用上述擴展卡爾曼濾波進行展開，用該點的雅可比矩陣求取卡爾曼增益，然后再利用卡爾曼濾波方法進行估計，因此式（1）的擴展卡爾曼濾波過程為：

[Δxk，k-1=f（Δxk-1，Δuk-1）Δxk=Δxk，k-1+Kk（Δyk-H（Δxk，k-1，Δuk））]

（11）

3.2 無味卡爾曼濾波器設計

無味卡爾曼濾波器（UKF）是基于無味變換的非線性卡爾曼濾波器，通過構造加權樣本點對參數估計，避免對非線性模型的線性化處理，可以直接用來對非線性系統狀態進行估計，其過程如下[7]：

下面將根據[k-1]時刻的狀態估計值[xk-1]和[Py-1]，給出求k 時刻的狀態估計[xk]和[Py]的實現過程。

1） 根據[xk-1]和[Py-1]，構造Sigma 點[χk-1']，[ i=1，…，2n]。

2） 計算預測 Sigma 點和均值

[χk|k-1i=fk（χk-1i）]

[xk|k-1=i=02nW（m）iχk|k-1i]

[Pk|k-1=i=02nW（c）iχk|k-1i-xk|k-1χk|k-1i-xk|k-1T+Qw，k]

3）修正（測量更新）

[Yk|k-1i=g（χk-1i）]? ? ? ? ? ? ? ? ? ? ? ? （12）

[yk|k-1=i=02nW（m）iYk|k-1i]

[Py，k=i=02nW（c）iYk|k-1i-yk|k-1Yk|k-1i-yk|k-1T+Rv，k]? ? ? ? ? ? ? （13）

[Pxy，k=i=02nW（c）iχk|k-1i-xk|k-1Yk|k-1i-yk|k-1T]

（14）

[Kk=Pxy，kP-1xy，k]

[xk=xk|k-1+Kk（yk-yk|k-1）]

[Pk=Pk|k-1-KkPy，kKTk]

通過上述兩種濾波方式分析對比，發現卡爾曼濾波（EKF）算法具有計算簡單、魯棒性強等優點，而無味卡爾曼濾波雖然解決了濾波發散等問題，但是由于其需要多次調用非線性模型進行參數估計，所以計算時間較長，實時性較差，為了保證參數在線估計，本文選取卡爾曼濾波對汽輪機運行狀態的參數進行評估，以此判斷其所處的狀態。

4 仿真實例

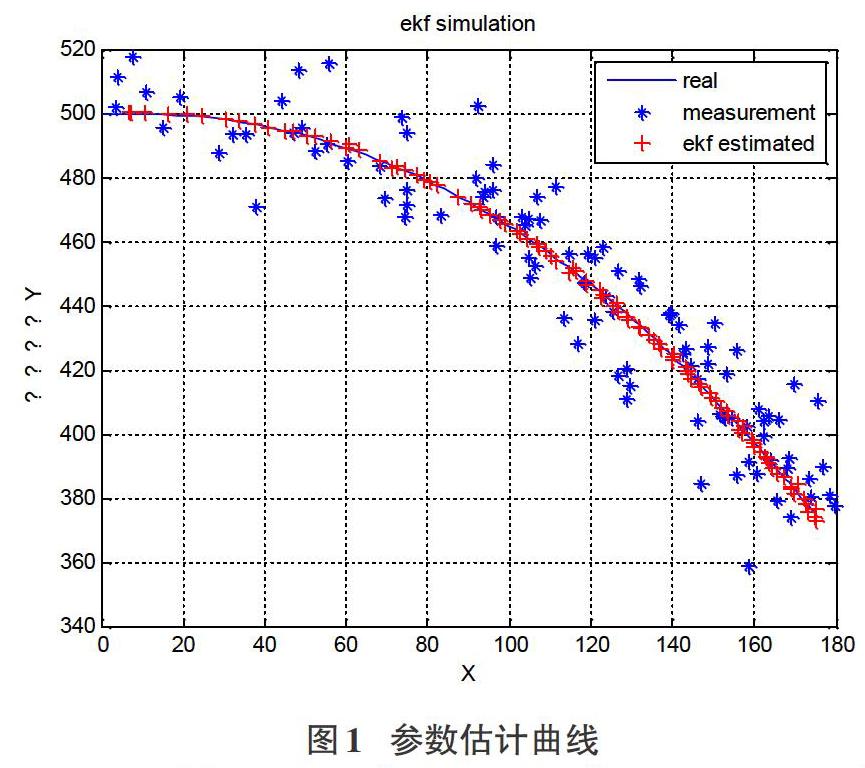
利用本文中的擴展卡爾曼濾波對某汽輪機旋轉軌跡進行追蹤，通過測量軸中心線實際的位移與期望軌跡進行對比，得出參數估計曲線如圖1所示。

經分析可知，在仿真用時和模型調用次數方面，對于擴展卡爾曼濾波估計方法而言，由于再迭代計算過程中不需要多次調用非線性模型，所以在很短時間內就能追蹤到軸中心的運動軌跡，這點區別于UKF，其調用次數最多，同時A，C矩陣的求取過程計算量也比較大，同樣會影響仿真用時;特別是在后期，迭代到一定次數EFK預測軌跡于期望軌跡重合度很高。

5 結論

本文采用卡爾曼濾波方法對火力發電中汽輪機的運動參數進行估計和預測，同時對比了擴展卡爾曼濾波和無味卡爾曼濾波在參數估計過程中速度，結果表明無味卡爾曼濾波雖然在求解過程中采用靈活的周期更新算法，但是其計算時間較長，在實時性方面不如擴展卡爾曼濾波，因此擴展卡爾曼濾波是一種實時性較高的參數估計方法。

參考文獻：

[1] 盛鍇，魏樂，江效龍，尋新. 基于PSASP和Simulink的汽輪機調節系統建模與仿真校核[J]. 中國電力，2015，48（02）：1-6+26.

[2] 付文鋒，楊新健，周蘭欣，陳林霄，吳瑞康，王喆. 某600MW汽輪機低壓末級排汽通道耦合流動三維數值模擬及其結構優化[J]. 中國電機工程學報，2014，34（14）：2267-2273.

[3] 趙洪山，田甜. 基于自適應無跡卡爾曼濾波的電力系統動態狀態估計[J]. 電網技術，2014，38（01）：188-192.

[4] 李江，王義偉，魏超，張鵬. 卡爾曼濾波理論在電力系統中的應用綜述[J]. 電力系統保護與控制，2014，42（06）：135-144.

[5] 韓萍，桑威林，石慶研. 一種新型非線性卡爾曼濾波方法[J]. 儀器儀表學報，2015，36（03）：632-638.

[6] 夏楠，邱天爽，李景春，李書芳. 一種卡爾曼濾波與粒子濾波相結合的非線性濾波算法[J]. 電子學報，2013，41（01）：148-152.

[7] 焉曉貞，羅清華. 基于卡爾曼濾波的動態傳感數據流估計方法[J]. 儀器儀表學報，2013，34（08）：1847-1854.