次梯度外梯度方法求解隨機(jī)變分不等式

張小娟

?

次梯度外梯度方法求解隨機(jī)變分不等式

張小娟

（重慶師范大學(xué)數(shù)學(xué)與科學(xué)學(xué)院，重慶 401331）

隨機(jī)變分不等式在供應(yīng)鏈網(wǎng)絡(luò)、交通運輸和博弈論中具有廣泛的應(yīng)用。提出基于次梯度外梯度的隨機(jī)逼近方法求解隨機(jī)變分不等式，將矯正步的投影改投在半空間，以此來減少計算投影的代價。在適當(dāng)?shù)募僭O(shè)下，證明了所提出的算法具有全局收斂性。

隨機(jī)變分不等式；隨機(jī)逼近；投影算法；次梯度外梯度；全局收斂性

0　引言

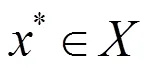
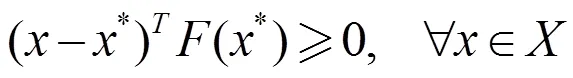
目前求解問題(1)最常用的方法主要有兩類，其一是樣本均值逼近(SAA)方法，其二是隨機(jī)逼近(SA)方法。SA方法每次取樣本的個數(shù)少，數(shù)值表現(xiàn)好于SAA。因此，本文主要考慮SA方法解問題(1)。最近Xu等人[3]提出基于基本投影的SA方法求解問題(1)，在強(qiáng)單調(diào)并且Lipschitz連續(xù)下依概率1收斂。隨后有學(xué)者提出基于正則化投影的SA方法求解問題(1)[4-5]，在單調(diào)并且Lipschitz連續(xù)下依概率1收斂。最近Kannan等人[6]提出了基于外梯度的SA方法求解，在偽單調(diào)并且有界或者Lipschitz連續(xù)下依概率1收斂。Iusem等人[7-8]修正外梯度算法，在偽單調(diào)并且Lipschitz連續(xù)下依概率1收斂。

基本投影需要一次投影，計算量小，但實際效果不好。外梯度方法明顯好于基本投影方法，但當(dāng)投影難以計算的時候外梯度方法計算代價大。為此本文結(jié)合兩種投影的優(yōu)點，受確定性VI問題次梯度外梯度算法[9]的啟發(fā)，將基于外梯度的SA方法的第二次投影改投在一個半空間上，提出基于次梯度外梯度的SA方法求解問題(1)，該方法減少了計算代價，在適當(dāng)?shù)募僭O(shè)下獲得全局收斂性。……