自適應非局部均值及在軸承故障檢測中的應用*

唐曉紅, 胡俊鋒,2, 熊國良, 張 龍

(1. 華東交通大學機電與車輛工程學院 南昌，330013) (2. 中國鐵路南昌局集團有限公司科學技術研究所 南昌，330002)

引 言

在旋轉機械中，滾動軸承是運用最為廣泛的關鍵零部件之一。隨著機械內部結構復雜程度的不斷提高，各零部件之間的聯系顯得極為緊密，而軸承的運轉狀態決定了其常處于高速高溫的惡劣環境下，極易發生損傷類故障[1-2]。為了提高機械設備的安全性和可靠性，減少不必要的經濟損失及人員傷亡，開展機械設備狀態監測與故障診斷研究成為現代工業化建設亟待解決的熱點問題[3]。近年來，對于機械設備的故障診斷研究已經取得了一定進展，一系列優異的消噪算法如譜峭度[4]、小波變換[5]和最小熵解卷積[6]等均得到了國內外學者的廣泛關注并成功應用于軸承的故障診斷研究，然而這些算法均存在一定的局限性，如譜峭度只反映沖擊性不反映周期性，小波變換基函數選取困難，這些不足均會導致診斷效果不佳。

非局部均值算法是近年來圖像處理領域的新興算法之一，是Buades等[7]為了解決傳統消噪方法在圖像信號處理出現的無法很好的保留圖像細節及邊緣的問題而提出的一種新的消噪方法。該算法在圖像處理領域的應用極為廣泛，在ECG信號[8]及疊前地震信號[9]的處理中也體現出優異的消噪效果。文獻[10]將NLM算法應用于軸承振動數據中的測量噪聲消除，然后將處理后的信號通過經驗模態分解(empirical mode decomposition，簡稱EMD)來消除其他噪聲干擾，最后對本征模函數(intrinsic mode function，簡稱IMF)包絡譜進行分析,成功提取出故障特征頻率。Lü等[11]對傳統的NLM算法進行了適當改進，提出了快速NLM算法。文獻[12-13]為了解決NLM算法處理低信噪比時出現的故障沖擊均值化問題，利用加權運算得出的權重曲線以突顯故障沖擊特征。總體來說，NLM算法在軸承故障診斷研究中仍然處于初級階段，存在許多問題有待解決，如NLM算法的濾波效果很大程度上取決于λ，M和P 3個參數的選擇，而上述研究均未對該問題進行深入探討。

筆者針對NLM參數難以選取的問題，提出采用粒子群算法(particle swarm optimization, 簡稱PSO)對NLM的3個決定性參數進行優化選擇，實現NLM參數的自適應選取，并通過軸承故障仿真數據和實驗數據對該方法進行了驗證。

1 方法介紹

1.1 非局部均值算法

NLM算法的原理是利用圖像中存在的眾多相似結構的特性，以像素點所在領域為單元，在圖像中搜索與該單元相似的成分，并對這些相似成分加權平均操作，以此消除圖像中的異常噪聲。Buades等[7]提出NLM算法的同時證明了其一致性，即NLM算法并非只對特定的像素點有效，而是適用于圖像中的任一像素點，即在自然圖像中，任一結構均存在與之類似的結構樣本。這些相似特性不僅表現在二維圖像中，在一維信號中也具有廣泛體現。

假設u(t)為真實軸承故障信號，n(t)為背景噪聲干擾，則實際采樣得到的帶噪聲信號v(t)表示為

v(t)=u(t)+n(t)

(1)

對于v(t)而言，基于NLM的數據處理的目的是從包含噪信號v(t)中消除噪聲干擾n(t)，從而恢復真實狀態下的故障信號u(t)的過程。u(t)的NLM算法估計值K(t)為

(2)

其中：N為以點t為中心的搜索范圍；N(t)為搜索區域內所有點的集合。

Z(t)為歸一化因子，其計算公式為

Z(t)=∑s∈N(t)ω(t,s)

(3)

其中：ω(t,s)表示權重。

ω(t,s)計算公式為

(4)

其中：d2為t和s兩點鄰域塊之間歐氏距離的平方和，歐式距離越小，兩者的相似程度越大；參數h=λ(2LΔ)1/2，控制權重ω(t,s)的衰減速度，即直接決定信號的最終濾波程度；Δ表示以點t為中心的鄰域塊；LΔ為以點s為中心的鄰域塊；λ為帶寬參數。

ω(t,s)的大小取決于以t和s為中心的兩個鄰域塊之間的相似程度，兩者相似度越高，則ω(t,s)的取值越大，反之亦然。ω(t,s)取值滿足0≤ω(t,s)/Z(t)≤1和∑jω(t,s)=1兩個基本條件。

參數λ，M和P為NLM算法的決定性參數，控制著NLM的最終處理效果。三者關系如圖1所示，參數P控制著鄰域塊的大小，即LΔ=2P+1；參數M為搜索區域N(t)長度的一半，理論上來說，M越大，則N(t)中的相似鄰域塊越多，NLM加權平均后的處理效果越好，但是相應地需要更多的計算時間，嚴重影響計算效率。

圖1 NLM參數關系Fig.1 Illustration of NLM parameter relationship

1.2 粒子群算法

一群鳥在區域內尋覓食物，若該區域僅有一塊食物，那么找到食物的最簡單有效的方案便是搜索距離食物最近的鳥的周圍區域。受此啟發，Kennedy等[14]提出粒子群算法，該算法中的粒子飛行的行為規則類似于鳥類運動，從而使整個粒子群的運動表現出與鳥類覓食類似的特性，并通過群體中個體之間的協作和信息共享來尋求最優解。該算法魯棒性強、收斂速度快且并不依賴特定的求解模型，非常適合求解模型的優化問題[15]。

PSO在求解最優問題時，其最優解對應搜索區域中的一個粒子的位置。該區域中存在許多粒子，每個粒子都具有自身獨特的位置和速度以決定最終的飛行距離和方向。在搜索最優粒子前，首先需要初始化一些隨機粒子，每個隨機粒子均表示區域內的候選解，這些候選解的優劣程度將由適應度值進行評估。粒子通過不斷迭代來尋找最優解，在每一次的迭代中，粒子通過跟蹤個體極值點Pbest(粒子本身找到的最優解)和全局極值點Gbest(整個種群目前找到的最優解)來更新自己。

設d維空間中粒子i的當前位置和速度分別為Xi=[xi,1, xi,2, …, xi,j]，Vi=[vi,1, vi,2, …, vi,j]；t時刻粒子i所經歷過的個體最優位置Pi,j=[pi,1, pi,2, …, pi,j]，在此記為Pbest；則該時刻群體中所有粒子經歷過的全局最優位置Gj=[g1, g2, …, gj]，記為Gbest。對于每一代粒子，其第j維粒子在尋覓到Pbest和Gbest兩個極值后，將通過這兩個最佳位置按照下式更新各粒子的速度和位置

vi,jt+1=ωvi,jt+c1r1pi,j-xi,jt+

c2r2pg,j-xi,jt

(5)

xi,jt+1=xi,jt+vi,jt+1

(j=1,2,…,d)

(6)

其中：ω為慣性權重；c1和c2為正的學習因子，亦被稱為加速常數，一般來說c1=c2，取值在0～4之間；r1和r2為0～1之間均勻分布的隨機數。

在PSO迭代尋優過程中，需要對位置變量Xi,j和速度變量Vi,j進行約束以確保算法的收斂性，約束條件如下：當Xi,jXmax時，Xi,j=Xmin+rand(Xmax-Xmin)；當Vi,jVmax時,Vi,j=Vmax。其中：Xmin和Xmax分別為粒子處于每一維時候的最小和最大位置；rand(·)為0～1之間隨機變化的數值；Vmax為粒子允許的最大運行速度。

2 PSO優化NLM的滾動軸承故障診斷模型

在NLM算法中，λ，M和P控制著該算法的最終處理效果，是NLM算法的決定性參數。利用PSO算法的尋優特性對這3個參數進行最優求解。在PSO算法中，目標函數即適應度的選擇決定了最終求解的準確性，對于滾動軸承故障數據而言，故障診斷的實質在于消除背景噪聲干擾、從而突出能夠反映軸承故障的相關信息，診斷精度一定程度上取決于故障信息的提取程度。峭度指標是常用的判別故障嚴重與否的評估指標之一，對異常沖擊特別敏感，能夠隨著異常沖擊的凸顯而增大。筆者采用峭度的倒數作為PSO的目標函數，即濾波效果越好，沖擊凸顯越明顯，則峭度值越大，其倒數(目標函數適應度)越小。PSO優化NLM的滾動軸承故障診斷模型如圖2所示。首先，設置好PSO參數；其次，以原始振動數據為對象，通過PSO的參數迭代逐步逼近期望輸出，直至實際輸出滿足閾值條件或達到最大迭代次數，獲得最優參數組合；最后，以最優參數構成NLM濾波器對信號濾波處理，通過包絡譜分析得出診斷結果。診斷步驟如下:

1) 輸入原始信號(signal)；

2) 給定初始條件，設置學習因子c1=c2=1.496 18，權重ω=0.729 8，適應度值閾值為0.01，最大迭代次數K=50，種群個體數目N=50；

3) 構造N個長度為3(參數λ，M和P)的向量X和V，分別代表種群的位置和速度，并初始化；

4) 計算粒子的適應度值，并初始化Pbest和Gbest；

5) 更新粒子位置和速度；

6) 比較每個粒子的適應度與經歷最優位置時的適應度Pbest，若當前更好，則更新Pbest；

7) 比較每個粒子的適應度和群體經歷最優位置的適應度Gbest，若當前更好，則更新Gbest；

8)重復步驟5～7，N次后獲得最優Pbest和Gbest；

9) 判斷Pbest(實際輸出)是否小于閾值0.01(期望輸出)，若不滿足條件則重復步驟5～8，直至滿足閾值條件或達到最大迭代次數進入下一步；

10) 輸出最優λ，M和P參數；

11) 將最優參數代入NLM算法獲得最優濾波器；

12) 對原始振動信號濾波處理得到NLM濾波信號；

13) 對濾波信號包絡計算后進行包絡譜分析，從中提取出故障特征頻率；

14) 提取出的故障特征頻率與理論故障特征頻率對比，判別是否存在故障，得到診斷結果。

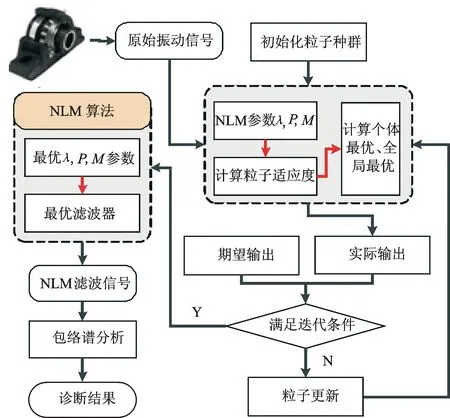
圖2 PSO優化NLM的滾動故障診斷模型Fig.2 Rolling bearing fault diagnosis model with NLM optimized by PSO

3 仿真信號分析

為了驗證所提方法在軸承故障診斷中的可行性和有效性，建立軸承響應函數并通過“rand”函數加入高斯噪聲干擾以模擬現實狀態下的軸承外圈故障數據，設置仿真信號的采樣頻率fs=12 kHz，外圈故障特征頻率為80 Hz。外圈故障仿真信號時域波形圖如圖3(a)所示。由于加入高斯噪聲程度較大，原始信號中的極大一部分故障沖擊特征被背景噪聲掩蓋，無法直觀地判別故障沖擊的位置，亦難以判別故障類型。因此需要對圖3(a)進一步處理消除背景噪聲以凸顯故障沖擊成分。圖3(b)PSO收斂曲線可以看到隨著參數的更替及迭代次數的遞進，適應度值也在不斷減小，即PSO尋優求解過程中目標函數適應度(濾波信號峭度的倒數)不斷減小，相應地濾波信號后其噪聲逐漸消除，沖擊凸顯程度不斷增強，峭度隨之增大。當迭代次數到達50次時尋優過程結束，得到最優參數組合λ= 0.340 6，M=5，P=5。將最優參數代入NLM得到最優NLM濾波器，并對原始信號進行處理，得到的濾波信號如圖3(c)所示。相較圖3(a)，圖3(c)經過NLM濾波后的信號噪聲干擾被壓制到極小范圍，沖擊特征提取效果明顯。圖3(d)為對圖3(c)包絡計算后的包絡譜圖，發現能夠成功提取出故障特征頻率和倍頻成分，而其他頻率干擾較小，可見筆者提出的方法具有良好的消噪效果。

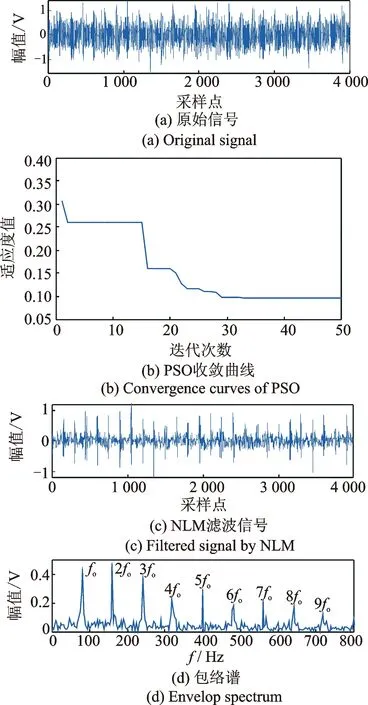
圖3 仿真信號PSO-NLM診斷過程Fig.3 Diagnostic procedure on simulation Signal using PSO-NLM

4 實驗數據分析

4.1 外圈故障分析

實驗室外圈故障數據來源于美國辛辛那提大學智能維護中心(IMS)[16]，軸承疲勞試驗臺的整體結構和局部照片分別如圖4(a)和圖4(b)所示。電機提供動力，通過帶傳動驅動主軸旋轉，主軸上依次安裝有4個型號為Rexnord ZA-2115的雙列圓錐滾子軸承。實驗過程中通過安裝于軸承座上的加速度傳感器對軸承狀態進行檢測，實驗時主軸轉速設定為2 kr/min，采樣頻率為20 kHz，采樣間隔為10 min。整個實驗過程共持續164 h，共采集數據文件984個，每個數據文件包含4列長為20 480點的數據，分別對應主軸上4個軸承的狀態。實驗結束后拆解裝置發現軸承1出現了嚴重外圈故障。Rexnord ZA-2115軸承參數及計算后得到的理論故障特征頻率如表1所示。

圖4 軸承疲勞試驗臺Fig.4 Fatigue test rig of rolling bearing

表1RexnordZA-2115軸承參數及故障特征頻率

Tab.1RexnordZA-2115bearingparameterandfaultcharacteristicfrequency

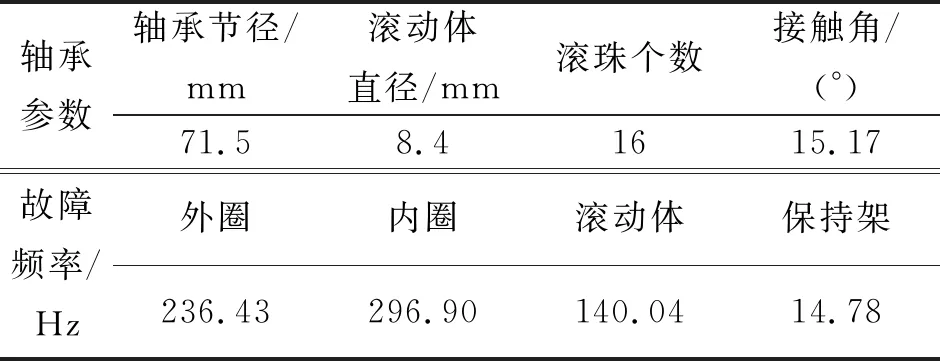
軸承參數軸承節徑/mm滾動體直徑/mm滾珠個數接觸角/(°)71.58.41615.17故障頻率/Hz外圈內圈滾動體保持架236.43296.90140.0414.78

本節分析的故障數據為984個文件中的第976個第1列數據，此時接近實驗尾聲，外圈故障已經較為嚴重，代表性較強。因數據點過大，在此僅截取其中的3 000點數據進行分析。圖5(a)為其時域波形圖，可發現由于背景噪聲較大，時域波形稍顯雜亂無章，因軸承故障引發的脈沖沖擊特征體現并不清晰，極大一部分故障脈沖隱藏于背景噪聲中。NLM算法自適應過程中的目標函數收斂曲線如圖5(b)所示，發現在優化過程中目標函數適應度逐步縮小，而NLM的峭度隨之逐漸增大，直至迭代至50次時優化結束，其最優參數最終確定為λ=0.144 1，M=7，P=6。根據該參數代入NLM算法得到的最優濾波器并對原始信號圖5(a)處理后的時域波形圖如圖5(c)所示。可以看到，處于圖5(a)的噪聲部分得到了極大程度的抑制，而能夠代表軸承故障信息的脈沖沖擊取得了極大的增強效果，相對于圖5(a)來說，故障點和故障位置已經能夠基本確定。圖5(d)濾波包絡譜能夠清晰地提取出故障特征頻率及其倍頻成分，而頻率的噪聲干擾成分被壓制到極小，因此可以判別出該軸承存在外圈故障，與實際情況相符。

圖5 實驗室外圈信號PSO-NLM診斷過程Fig.5 Diagnostic procedure on laboratory outer ring signal using PSO-NLM

4.2 內圈故障分析

為了進一步說明本研究方法在軸承故障診斷的有效性，采用美國凱斯西儲大學軸承數據中心[17]的軸承內圈故障數據進行分析。滾動軸承故障模擬實驗臺主要由左側的三相感應電機、中間的力矩傳感器、右端的測功機及內部控制模塊4部分組成。實驗臺的整體結構如圖6所示。

圖 6 滾動軸承故障模擬實驗臺Fig.6 Simulation test-bed of rolling bearing failure

該實驗臺可測試兩種型號的軸承，型號分別為SKF6205-2RS和SKF6203-2RS，分別安裝在電機驅動端和風扇端。采用電火花技術為軸承添加不同尺寸的點蝕故障，故障直徑依次為0.178，0.356和0.533 mm。軸承的工作狀態由安裝于電機驅動端、風扇端和底座的3個加速度傳感器進行記錄，由此采樣可得到所需的故障振動數據。選取的分析數據為驅動端SKF6205-2RS軸承內圈故障數據，其故障直徑為0.533 mm，實驗時的相關參數如下：電機轉速為1 797 r/min，采樣頻率為12 kHz。SKF6205-2RS軸承的相關參數及實驗狀態下的故障特征頻率如表2所示。

表2SKF6205-2RS軸承參數及故障特征頻率

Tab.2SKF6205-2RSbearingparameterandfaultcharacteristicfrequency

軸承參數軸承節徑/mm滾動體直徑/mm滾珠個數接觸角/(°)39.047.9490故障頻率/Hz外圈內圈滾動體保持架107.36162.1970.5811.93

圖7(a)為安裝在電機驅動端的加速度傳感器采樣得到的振動數據。為了凸顯本研究方法的診斷效果，通過“rand”函數加入了一定程度的高斯白噪聲干擾。由于噪聲比例較大，原始信號中代表故障信息的循環沖擊成分被背景噪聲壓制，很難從中提取出故障信息。通過PSO優化后獲得最優參數λ，M，P的數值分別為0.509 9，62和6，將之代入NLM算法得到最優濾波器。圖7(c)和圖7(d)分別為NLM濾波信號及其包絡譜。圖7(c)濾波信號中能夠明顯的提取出故障沖擊特征，而圖7(d)中故障特征頻率基頻及倍頻成分均清晰明了且譜線突出，倍頻譜線兩端存在明顯的轉頻邊帶，為典型的內圈故障，與內圈故障特征頻率理論值也完全對應。可見本研究方法在處理軸承內圈故障也同樣適用。

圖7 實驗室內圈信號PSO-NLM診斷過程Fig.7 Diagnostic procedure on laboratory inner ring signal using PSO-NLM

5 方案對比

在文獻[10-11]中，使用非局部均值算法對數據進行處理時，參數λ的取值通過SURE準則選擇。由于λ的取值直接影響到消噪后信號的平滑度，因此在上述文獻中根據SURE準則確定參數λ的取值為0.5σ，其中σ為信號的方差。由于參數M和P通過工作人員的經驗進行選取，因此數據處理結果受工作人員的主觀性思想影響較大，同樣的數據經過不同的工作人員呈現出結果的多樣性。為了便于直觀地體現本研究方法的優異性，以圖5(a)的外圈故障數據為例進行舉例說明。通過SURE準則選取λ=0.5，σ=0.187 8，根據經驗選擇參數M和P的值為10和10。將參數代入NLM后得到濾波器，對圖5(a)信號處理后得到的濾波信號如圖8(a)所示，其在時域波形圖中并未有明顯改善，故障沖擊仍處于噪聲淹沒狀態，而圖5(c)的噪聲消除效果極為優異，故障沖擊凸顯效果優勢較大。對比雙方包絡譜，圖8(b)雖然能得到故障特征頻率及其倍頻成分，但是4倍頻和5倍頻成分卻被噪聲頻率壓制，而圖5(d)則能清晰提取出4倍頻和5倍頻成分，且圖5(d)頻率的峰值能量也比圖8(b)略高。可見，從噪聲消除效果和包絡譜分析效果看，本研究方法優于傳統的NLM方法。

6 結束語

提出應用粒子群算法對參數進行尋優求解，實現了NLM算法的自適應化。針對軸承故障診斷領域建立了PSO優化NLM的滾動軸承故障診斷模型。運用仿真數據和實驗軸承內、外圈故障數據對所提模型進行了驗證。結果證明，本研究方法能夠較大幅度地消除噪聲，并提取出故障信息，對于算法的普及和應用有著十分積極的作用。