GFD和核主元分析的機(jī)械振動特征提取*

韋 祥， 李本威， 吳易明

(1.海軍航空大學(xué)航空基礎(chǔ)學(xué)院 煙臺,264001) (2.洛陽軸承研究所有限公司 洛陽,471039)

引 言

轉(zhuǎn)子系統(tǒng)是代表一類廣泛工程應(yīng)用背景的復(fù)雜機(jī)械的關(guān)鍵部分，由于材料本身的非線性物理性質(zhì)、部件之間的間隙和摩擦耦合作用、滑動軸承的油膜力、滾動軸承中的間隙和恢復(fù)力、裂紋、大位移或者大變形[1]等因素導(dǎo)致系統(tǒng)振動響應(yīng)具有強(qiáng)烈的非線性性質(zhì)，采用線性分析的方法來研究系統(tǒng)的動態(tài)特性會“濾掉”許多與系統(tǒng)故障密切相關(guān)的非線性現(xiàn)象[2]。近年來，隨著非線性動力學(xué)的發(fā)展，“非線性動力學(xué)指數(shù)(最大Lyapunov指數(shù)、分形維數(shù)和熵等)”被用于機(jī)械狀態(tài)監(jiān)控和故障診斷。該趨勢說明研究者逐漸開始從振動產(chǎn)生的機(jī)理去研究系統(tǒng)的運(yùn)動狀態(tài)、運(yùn)動穩(wěn)定性、混沌及分叉等現(xiàn)象，揭示振動行為的內(nèi)在演化過程。

傳感器測得的每一個振動信號都是一種動力學(xué)結(jié)構(gòu)在一維時域空間的表現(xiàn)，信號波形結(jié)構(gòu)蘊(yùn)含著參與動態(tài)變化的全部變量的信息。當(dāng)系統(tǒng)處于不同的故障狀態(tài)下，其內(nèi)在動力學(xué)結(jié)構(gòu)必然有差異。因此通過一個對動力學(xué)結(jié)構(gòu)敏感的參數(shù)對每個信號構(gòu)成的動力學(xué)結(jié)構(gòu)進(jìn)行定量化度量，即可實現(xiàn)對不同故障狀態(tài)的特征提取。分形維數(shù)用來描述具有無限精細(xì)、非常不規(guī)則、無窮自相似結(jié)構(gòu)和非整數(shù)維數(shù)的點集，是定量描述混沌吸引子的重要不變量。目前，分形維數(shù)(盒維數(shù)、信息維數(shù)、關(guān)聯(lián)維數(shù))在機(jī)械故障診斷領(lǐng)域(轉(zhuǎn)子、軸承和齒輪等)取得較大的發(fā)展[3-5]。然而，分形實際應(yīng)用中一般只考慮信號的單重分形特征，即認(rèn)為整個信號具有相同的尺度屬性，只能從整體上反映信號的不規(guī)則性，缺乏對局部奇異性的刻畫[6]。

廣義分形維數(shù)為復(fù)雜信號提供了一種集合結(jié)構(gòu)分析方法，相比單重分形維數(shù)能精細(xì)刻畫信號的局部尺度行為[7]，對不同運(yùn)動狀態(tài)的動力學(xué)結(jié)構(gòu)有良好的度量和較好的區(qū)分度。相比Lyapunov指數(shù)和關(guān)聯(lián)維數(shù)等參數(shù)需要估計相空間重構(gòu)的嵌入維數(shù)和時間延遲以及大計算量等缺點[8]，GFD只依賴于分割體的尺寸，有較高的計算效率。由于廣義分形維數(shù)提取的特征維數(shù)通常較高，所提取的高維特征中不乏冗余的信息，因此需對提取的高維特征進(jìn)行降維處理并實現(xiàn)不同故障的分類。

核函數(shù)主元分析通過選定的非線性核函數(shù)將輸入矢量映射到一個高維特征空間，使輸入矢量在該空間有更好的可分性，然后對高維空間的數(shù)據(jù)做主成份分析從而得到非線性主元，具有特征提取與分類器的作用[9-10]。KPCA在機(jī)械振動特征提取和分類存在以下不足。

1) KPCA特征提取與分類精度嚴(yán)重依賴初始特征的區(qū)分程度。KPCA處理之前需計算振動信號的最大峰值、絕對均值、有效值、方差、斜度和峭度等反映波形結(jié)構(gòu)的指標(biāo)，進(jìn)行初步特征提取，這些指標(biāo)選取的合適與否決定了KPCA分類的精度。早期微弱故障由于損傷性很小，產(chǎn)生的故障信號不太強(qiáng)烈，在振幅和頻域上表征不明顯，常規(guī)KPCA算法難以取得滿意的效果。此外，有些種類的故障特征區(qū)分度不夠明顯,也很難取得良好的分類效果。

2) 核函數(shù)中參數(shù)選取對分類精度影響較大，需不斷調(diào)整參數(shù)以獲得高精度的分類，方法不夠穩(wěn)健。

上述原因制約了KPCA的實際工程應(yīng)用能力。

筆者提出了GFD-KPCA的故障診斷方法，綜合利用GFD和KPCA方法的優(yōu)點克服兩種方法在工程應(yīng)用上的不足，具有良好的工程應(yīng)用價值。

1 振動信號的廣義分形維數(shù)

1.1 廣義分形維數(shù)的相關(guān)概念

設(shè)μ為R上的正的概率Borel測度，對于q≠1且ε>0,定義以下積分

(1)

(2)

對于離散數(shù)據(jù)，假定尺度ε的球是相空間的一個分割，記點集Ω落在尺度為ε的分割體中的概率是Piε，Renyi提出廣義熵

(3)

從而廣義維數(shù)定義為

(4)

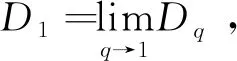
(5)

當(dāng)q=0,1,2時，Dq分別為盒維數(shù)D0信息維數(shù)D1和關(guān)聯(lián)維數(shù)D2。對于指數(shù)p≥q，存在Dp≥Dq的關(guān)系。

1.2 廣義分形維數(shù)的計算方法

目前，對于離散信號廣義分形維數(shù)的計算方法主要有3種：覆蓋法、固定半徑法和固定質(zhì)量法[12]，其中覆蓋法是研究分形最普遍的方法,其計算過程如下。

1) 信號離散。設(shè)實測振動信號采樣頻率為f，采樣時間為T，振動幅值為X，則采樣點數(shù)n=T/f，將信號進(jìn)行離散可得Tk,Xk，k=1,2,…,n。為便于計算其廣義分形維數(shù)，將離散后的信號進(jìn)行移位，使所有的點落入直角坐標(biāo)系的第1象限。

2) 網(wǎng)格劃分。取εj=2jΔt為網(wǎng)格寬度，其中:Δt=1/f;j為網(wǎng)格尺度劃分種數(shù)，則橫向網(wǎng)格數(shù)為

m=(maxX-min(X))/εj

(6)

縱向網(wǎng)格數(shù)n=T/εj。離散點Xk落在網(wǎng)格中的坐標(biāo)為M,N。其中

M=Xk/εj+1

(7)

N=Tk/εj+1

(8)

落入mn網(wǎng)格點數(shù)為dmn，網(wǎng)格mn覆蓋住集合的概率Pmnεj=dmn/n。通過改變ε的大小可以計算出一系列的Kqε，令Xj=Kqεj，Yj=lgεj。

3) 計算Dq。由以上幾步的計算，在lgε-Kqε的圖上得到標(biāo)度率存在的范圍，該范圍內(nèi)的斜率的絕對值就是給定參數(shù)q的Dq。對于無標(biāo)度區(qū)的選擇方法有很多，筆者直接采用最小二乘擬合的方法求解斜率。

設(shè)Yj=-DqXj+B，Dq為所求的斜率，則

(9)

需要特別注意的是，采用求斜率的辦法計算GFD時野點對其計算結(jié)果影響較大，在實際計算時要剔除野點。

2 核函數(shù)主元分析

核空間理論是針對測量空間中非線性問題或者線性不可分問題，通過尋找合適的非線性映射函數(shù)ΦX，將測量空間中的樣本集X映射到高維空間F中，使得線性不可分的問題在空間F中進(jìn)行分類。最早由Bernhard提出[13]，目前在機(jī)械領(lǐng)域已有成熟的運(yùn)用[14-16]。KPCA具體算法[17]如下。

非線性映射函數(shù)Φ:Rm→F，將輸入空間xkk=1,2,…,n映射到特征空間F：Φxk，k=1,2,…,n中。設(shè)F：Φ(xk)(k=1,2,…,n)已經(jīng)去均值，則在F空間上的協(xié)方差矩陣為

(10)

對矩陣CF做特征矢量分析。設(shè)其特征值為λ，特征矢量為V，λV=CFV，將每個樣本與該式做內(nèi)積，可得

λΦxk,V=Φxk,CFV(k=1,2,…,n)

(11)

則特征矢量V可用Φ(xk)線性表示為

(12)

其中：αj為相關(guān)系數(shù)。

聯(lián)立式(10)～(12)可得

(13)

定義一個n×n的方陣K

Kij=Φxi,Φxj

(14)

則式(13)可簡化為nλKα=K2α，由此可以看出，在特征空間F中做線性主元分析就相當(dāng)于求解式(14)的特征值和特征向量。矩陣K的特征值λ1≥λ2≥…≥λn，其對應(yīng)的特征向量為α1,α2,…,αn。為了達(dá)到降維的目的，可以選擇保留前pp≤n個特征值和特征向量。矩陣K可通過選擇核函數(shù)來確定。

為提取主元特征，需計算映射數(shù)據(jù)在特征空間F中的投影

(15)

目前，常用的核函數(shù)有高斯徑向基核函數(shù)、多項式核函數(shù)及神經(jīng)網(wǎng)絡(luò)核函數(shù)等。主元數(shù)目可通過主元貢獻(xiàn)率的方法進(jìn)行確定，其定義為

(16)

其中：Contrλk為第k個主元的貢獻(xiàn)率，表明第k個主元所包含的系統(tǒng)信息占全部信息的百分比。

為保證既最大化保留原有信息量的同時又實現(xiàn)特征空間的降維，要求p各主元的累計貢獻(xiàn)率CPV必須大于某一界限值，即

(17)

其中：CL為設(shè)定的界限值，通常取為85%。

3 GFD-KPCA機(jī)械故障特征提取

通過GFD-KPCA方法對旋轉(zhuǎn)機(jī)械進(jìn)行特征提取具體流程如圖1所示。

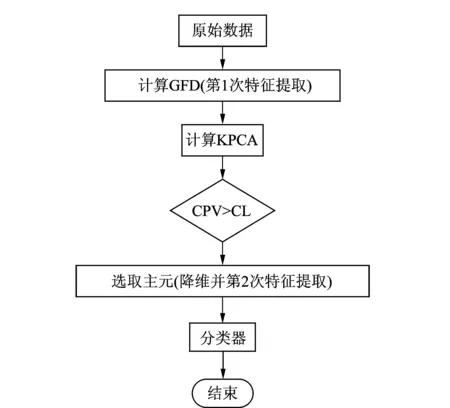
圖1 GFD-KPCA方法流程圖Fig.1 Flow chart of the GFD-KPCA method

為驗證方法的有效性，通過轉(zhuǎn)子實驗平臺測試數(shù)據(jù)、美國凱斯西儲大學(xué)(case western reserve university，簡稱CWRU)提供的典型軸承故障數(shù)據(jù)進(jìn)行驗證。

3.1 轉(zhuǎn)子振動GFD特征提取

轉(zhuǎn)子振動測量與診斷系統(tǒng)由轉(zhuǎn)子系統(tǒng)、控制采集系統(tǒng)和分析系統(tǒng)組成,如圖2所示。

圖2 轉(zhuǎn)子實驗臺及其測試系統(tǒng)Fig.2 Rotor test rig and the test system

圖3 轉(zhuǎn)子試驗器結(jié)構(gòu)Fig.3 Sketch of the rotor dynamics test rig

如圖3所示，轉(zhuǎn)子支撐結(jié)構(gòu)由電機(jī)、軸承、軸系及集中質(zhì)量等核心件組成，可模擬偏心、碰磨及不對中等故障。測量傳感器采用非接觸式電渦流位移傳感器測量軸的徑向位移，采用光電傳感器測量轉(zhuǎn)速、提供鍵相信號。分別取未加故障的轉(zhuǎn)子運(yùn)行狀態(tài)為正常狀態(tài)(樣本1)，圓盤加偏心質(zhì)量(樣本2)，軸周向輕微碰摩狀態(tài)(樣本3)，轉(zhuǎn)子偏心加不對中的狀態(tài)(樣本4)，轉(zhuǎn)速為4 kr/min，采樣頻率為5 kHz進(jìn)行隨機(jī)采樣，每種狀態(tài)選取64組數(shù)據(jù)，以32組數(shù)據(jù)作為KPCA算法的訓(xùn)練樣本，剩余的32組數(shù)據(jù)作為測試樣本。

通過對上述4種狀態(tài)的數(shù)據(jù)進(jìn)行廣義分形維數(shù)的計算，每種狀態(tài)采取穩(wěn)定的1 024個點，指數(shù)q范圍為[0,2.2]，步長為0.05，每種狀態(tài)獲得45個分形維數(shù)，以其中一組數(shù)據(jù)為例，結(jié)果如圖4所示。由圖4可知，良好狀態(tài)下廣義分形維數(shù)數(shù)值最小，偏心不對中耦合故障數(shù)值最大，這是由于良好狀態(tài)下信號最“規(guī)則”，耦合故障狀態(tài)下信號最“不規(guī)則”，說明廣義分形維數(shù)對系統(tǒng)不同狀態(tài)下的振動信號的復(fù)雜程度有著精確的刻畫，同時由廣義分形維數(shù)提取的特征對四種故障狀態(tài)有較好的區(qū)分度。

圖4 轉(zhuǎn)子廣義分形維數(shù)圖譜Fig.4 The GFD of rotor system

3.2 軸承典型振動故障GFD特征提取

CWRU為研究機(jī)械系統(tǒng)狀態(tài)評估、故障診斷等技術(shù)進(jìn)行了軸承故障模擬實驗，分別在軸承外圈、內(nèi)圈和滾珠上添加了直徑為0.177 8～1.016 mm的故障，通過加速度傳感器獲得振動信號[18]。選取1 797 r/min、故障直徑為0.177 8 mm狀態(tài)下的內(nèi)圈、滾珠、外圈故障進(jìn)行GFD-KPCA特征提取。每種故障選取8組數(shù)據(jù)，共24組數(shù)據(jù)。以其中一組數(shù)據(jù)為例，其GFD結(jié)果如圖5所示。圖5可知，GFD對軸承不同故障狀態(tài)具有較好的區(qū)分度。

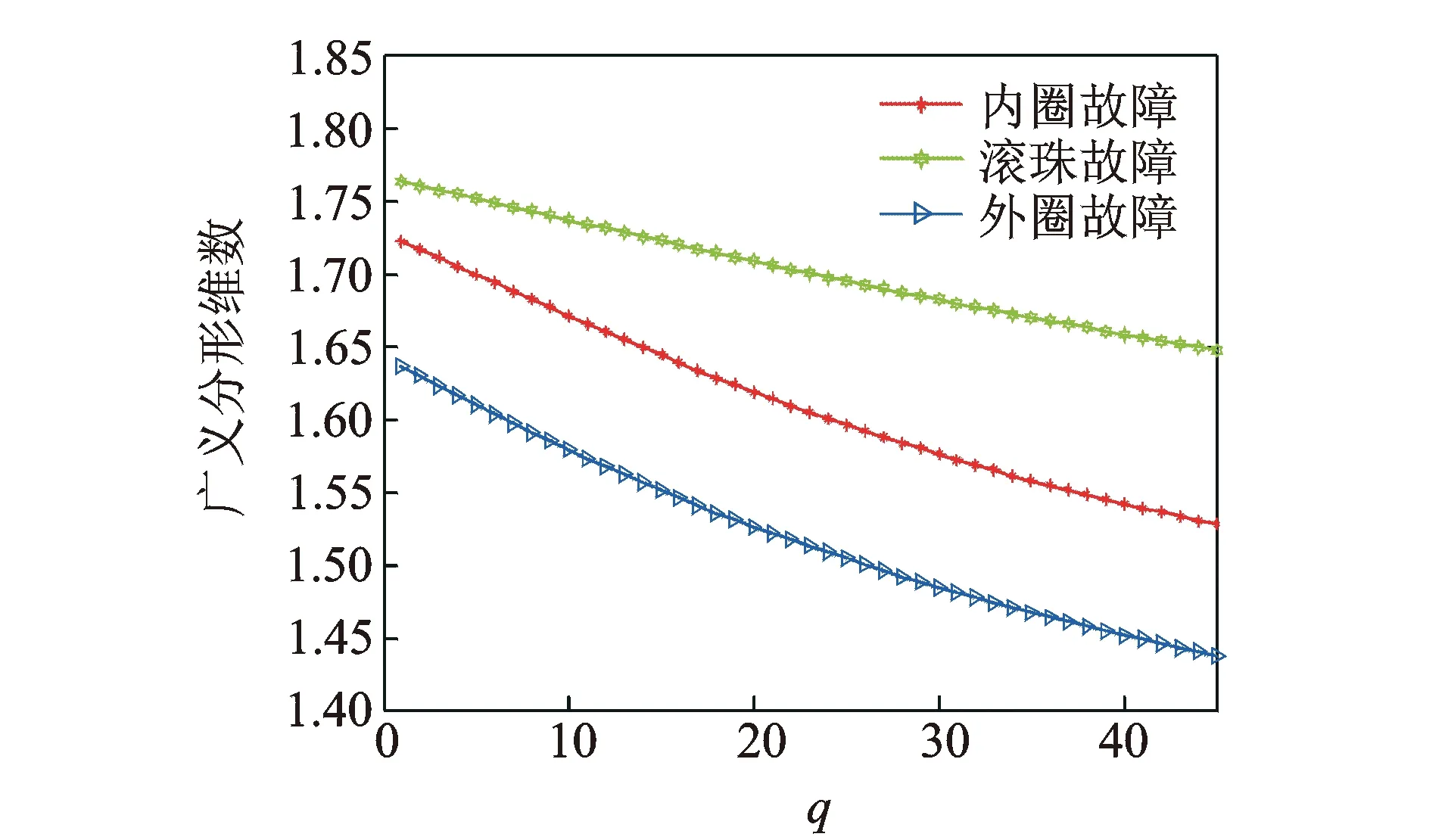
圖5 軸承廣義分形維數(shù)圖譜Fig.5 The GFD of bearing system

3.3 KPCA二次特征提取

通過廣義分形維數(shù)對轉(zhuǎn)子與軸承不同狀態(tài)進(jìn)行初步特征提取，獲得45維的高維特征空間。高維特種空間中，特征之間存在一定的冗余，需對特征進(jìn)行降維。有研究表明[12]，支持向量本身對不同的方法具有不敏感性，即選用不同的核函數(shù)得到的分類結(jié)果較為接近，因此筆者選取高斯徑向基核函數(shù)(式18)對原始狀態(tài)征兆集進(jìn)行核函數(shù)主元分析，實現(xiàn)高維特征空間的降維與故障分類。

(18)

KPCA算法求得轉(zhuǎn)子系統(tǒng)和軸承系統(tǒng)主元累計貢獻(xiàn)率如表1所示。從表1可知，前3個主元已經(jīng)包含了系統(tǒng)的全部信息，因此保留前3個主元作為系統(tǒng)的特征值，即特征空間由45維降低為3維空間。

表1 主元貢獻(xiàn)率

4 特征提取方法有效性驗證

特征提取的目的是從眾多特征中求出對分類識別最有效的特征，從而實現(xiàn)特征空間的壓縮，并使不同狀態(tài)數(shù)據(jù)類內(nèi)距離最小、類間距離最大。KPCA算法在特征提取的同時具有分類器的功能，將用于測試的32個轉(zhuǎn)子故障樣本輸入訓(xùn)練好的KPCA模型，其分類結(jié)果如圖6所示。由圖6可知，轉(zhuǎn)子系統(tǒng)4種狀態(tài)下的數(shù)據(jù)各自形成聚類中心，并進(jìn)行了正確的分類。同樣，將用于測試的軸承24個故障樣本輸入訓(xùn)練好的KPCA模型，其分類結(jié)果如圖7所示。由圖7可知，軸承在3種故障狀態(tài)下的數(shù)據(jù)各自形成聚類中心，并進(jìn)行了正確的分類。

圖6 轉(zhuǎn)子KPCA分類結(jié)果Fig.6 Classification of rotor system using KPCA method

圖7 軸承KPCA分類結(jié)果Fig.7 Classification of bearing system using KPCA method

為進(jìn)一步驗證分類的有效性，選取最常用的K近鄰(K nearest neighbor，簡稱KNN)算法作為分類器，主要是因為與其他具有較強(qiáng)學(xué)習(xí)能力的分類器相比，KNN的分類結(jié)果更依賴于數(shù)據(jù)特征而非分類器本身。同時，GFD-KPCA特征提取方法中，徑向基核函數(shù)中的參數(shù)σ對特征提取和分類結(jié)果影響較大，嚴(yán)重制約了KPCA的工程應(yīng)用。為研究GFD-KPCA特征提取方法的適用性，對不同σ取值情況下的KNN算法分類情況進(jìn)行研究，結(jié)果如圖7所示。KNN算法分類正確率結(jié)果隨σ取值的增大而增大，當(dāng)σ≥2時，分類正確率達(dá)穩(wěn)定值，轉(zhuǎn)子故障確分率達(dá)到96.88%，即錯分1個數(shù)據(jù)，軸承故障確分率達(dá)到91.67%，即錯分2個數(shù)據(jù)。說明GFD-KPCA特征提取方法對于σ取值有較寬的適用性和較高的分類識別率，從而驗證了方法特征提取的有效性。

圖8 σ與KNN算法確分率的關(guān)系Fig.8 The relationship between σand classification accuracy in KNN

5 特征提取方法穩(wěn)健性驗證

KPCA算法的分類精度嚴(yán)重依賴于初始特征的區(qū)分度，為了說明算法的適用性和穩(wěn)健性，筆者利用通過美國智能維數(shù)系統(tǒng)中心(intelligent maintenance systems，簡稱IMS)的軸承疲勞試驗數(shù)據(jù)對GFD-KPCA的早期微弱故障特征提取能力進(jìn)一步研究。

軸承早期故障具有特征不明顯、信號微弱、信噪比低及故障識別難等特點，是軸承狀態(tài)監(jiān)控的難點和熱點問題。IMS進(jìn)行了軸承疲勞試驗，實驗裝置可參考文獻(xiàn)[19-20]。一個軸上安裝了4套RexnordZA-2115雙列滾子軸承。軸的轉(zhuǎn)速保持2 kr/min恒定不變，通過彈簧裝置在軸上加載2 721.554 kg的徑向載荷。所有軸承潤滑固定，并且每個軸承座都安裝2個PCB加速度傳感器用來采集軸承的振動數(shù)據(jù)。振動信號每隔10 min采集一次，采樣長度為20 480個點，采樣頻率為20 kHz。試驗臺中的4套軸承從2月12日11:16:18運(yùn)行至2月19日06:22:39，一共采集到984個文件數(shù)據(jù)。在疲勞實驗結(jié)束時，軸承1檢測到外圈故障。文獻(xiàn)[21]檢測到早期故障是在第541個文件，對應(yīng)試驗時間為2月16日04:42:39。疲勞實驗數(shù)據(jù)及早期故障點如圖9所示。由圖9可知,系統(tǒng)在產(chǎn)生早期微弱故障時其振動信號結(jié)構(gòu)相對于正常狀態(tài)并未產(chǎn)生明顯的突變。

圖9 IMS軸承疲勞試驗Fig.9 Bearing fatigue test in IMS

選取正常階段和早期磨損階段各100個文件，每個文件中選取3 000個數(shù)據(jù)點進(jìn)行GFD計算。以第1個文件和541個文件數(shù)據(jù)為例，其GFD結(jié)果如圖10所示。每種狀態(tài)選取50組數(shù)據(jù)作為訓(xùn)練和測試樣本，GFD-KPCA特征提取及分類如圖11所示。

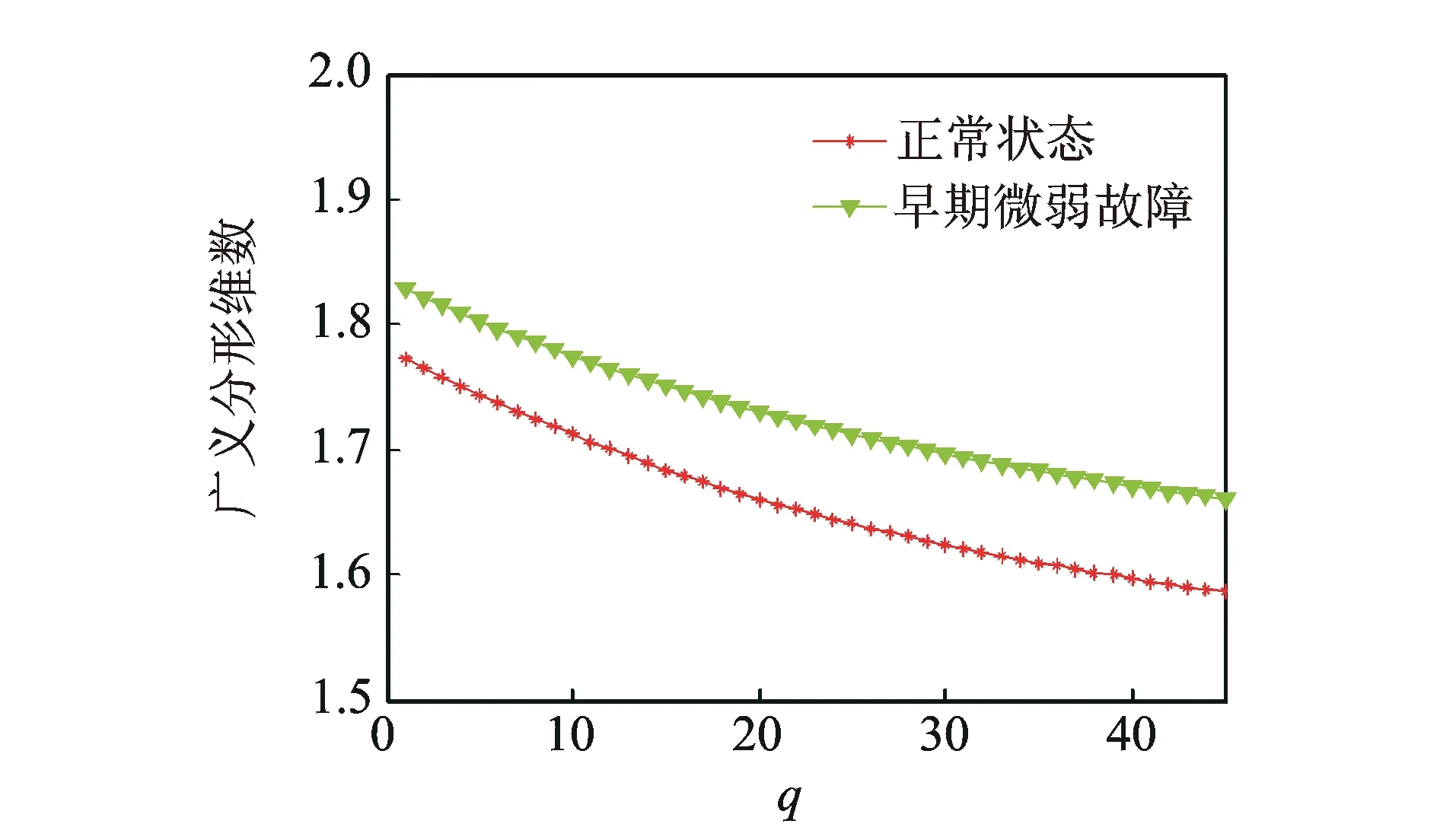
圖10 軸承早期微弱故障廣義分形維數(shù)Fig.10 GFD of bearing early weak fault

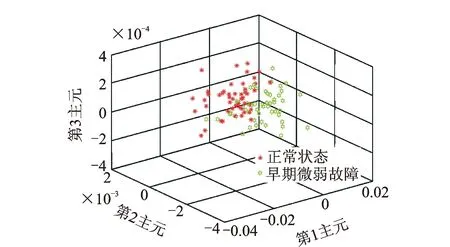
圖11 IMS軸承GFD-KPCA特征提取結(jié)果Fig.11 Bearing feature extraction using GFD-KPCA method

由圖10可知，當(dāng)軸承產(chǎn)生輕微早期磨損故障時，其內(nèi)在的動力學(xué)結(jié)構(gòu)已經(jīng)發(fā)生改變，GFD可以敏銳捕捉這種細(xì)微變化，對兩種動力學(xué)結(jié)構(gòu)有著良好的區(qū)分。圖11的KPCA分類結(jié)果顯示正常狀態(tài)和早期微弱故障狀態(tài)形成了良好的分類。當(dāng)σ≥2時,KNN算法的確分率穩(wěn)定在89%，即錯分11個數(shù)據(jù)。

相比轉(zhuǎn)子實驗和CWRU的典型故障數(shù)據(jù)，IMS軸承早期故障特征和正常狀態(tài)并未有明顯的區(qū)分，且選取樣本的是一段時間的動態(tài)數(shù)據(jù)，GFD-KPCA依舊獲得較好的分類精度，說明GFD-KPCA方法對于機(jī)械振動特征提取具有良好的適應(yīng)性和穩(wěn)定性。

圖12 IMS軸承常規(guī)KPCA特征提取結(jié)果Fig.12 Bearing feature extraction using normal KPCA method

為了進(jìn)一步說明GFD-KPCA的優(yōu)越性，與常規(guī)KPCA特征提取方法進(jìn)行對比驗證。選取最大峰值、絕對均值、均方根幅值、方差、偏斜度、峭度、波形指標(biāo)、脈沖指標(biāo)及裕度指標(biāo)作為初步特征提取的參數(shù)[14]。同樣對IMS數(shù)據(jù)進(jìn)行KPCA特征提取，結(jié)果如圖12所示。圖中顯示KPCA對數(shù)據(jù)進(jìn)行了一定的分類，KNN算法顯示常規(guī)KPCA對IMS數(shù)據(jù)最高分類精度為80%，即錯分20個點。

與常規(guī)KPCA算法相比，GFD-KPCA算法對動力學(xué)結(jié)構(gòu)有個更為精細(xì)地刻畫，不同狀態(tài)下振動提取的特征更為準(zhǔn)確。無論是對于典型故障還是微弱故障都有較好的提取能力，適用性和穩(wěn)健性更好。

6 結(jié) 論

1) GFD算法對振動信號的動力學(xué)結(jié)構(gòu)有精確的刻畫，對不同運(yùn)行狀態(tài)(包括故障狀態(tài))具有良好的區(qū)分度，優(yōu)于常規(guī)的振動特征提取方法，與KPCA結(jié)合可明顯提高旋轉(zhuǎn)機(jī)械的特征提取精度。

2) 對IMS軸承微弱故障特征提取說明GFD-KPCA相比常規(guī)的KPCA特征提取方法具有更好的適用性和穩(wěn)健性，彌補(bǔ)了常規(guī)KPCA算法由于初始特征區(qū)分度差導(dǎo)致分類精度差的不足。

3) GFD-KPCA 算法對核函數(shù)可變參量依賴性較小，適用范圍寬，在σ≥2情況下，只依賴距離測度的KNN算法即可滿足較高的確分率，具有良好的工程應(yīng)用價值。

4) GFD-KPCA方法也存在一定的不足，若不同故障之間區(qū)別度較大，只需少量數(shù)據(jù)進(jìn)行GFD-KPCA計算即可實現(xiàn)故障的特征提取。當(dāng)特征區(qū)分度不明顯時則需較大的數(shù)據(jù)量，導(dǎo)致了計算效率的不足。