超聲固結區域溫度場分析及實驗研究*

王 寅， 曹 俊， 廖夢嬌， 肖中揚， 張會霞， 黃衛清

(1.華僑大學機電及自動化學院 廈門，361021) (2.南京航空航天大學航空宇航學院 南京，210016) (3.廣州大學機械與電氣工程學院 廣州，510006)

引 言

超聲固結金屬增材制造技術是利用超聲波的高頻振動與靜壓力作用，促使金屬箔材之間產生摩擦、塑性變形等效應，促進界面區域金屬原子產生結合與擴散，實現層與層之間的固態冶金結合。這種通過逐層固結的方法實現高性能結構的制造是一種綠色、高效、低成本的先進制造技術[1-2]。

超聲固結區域溫度對界面結合強度、界面應力分布有顯著影響。溫度過低，嚴重影響接頭質量；溫度過高，將直接對埋入金屬基體中的功能材料或元器件造成損傷[3]。因此，研究固結接頭處溫度的變化趨勢將有助于獲得良好的固結質量，提高加工效率。但是在超聲固結過程中，由于固結區域相對狹窄，并有高頻振動和集中壓應力的作用，難以通過常規的測量手段測量實時固結溫度數據，導致溫度與工藝參數的相互耦合關系難以明確，阻礙了工藝參數進一步優化。為了獲得工藝參數對固結過程中溫度的影響規律，現有的研究主要通過以下3個方面來研究導致溫度變化的直接因素。

1) 局部應力對溫度的影響。Gao等[4]基于固結區域的摩擦邊界定義，對超聲波點焊進行了二維數值模擬，發現摩擦力和壓力是影響結合區域應變場形成的主要因素。文獻[5-6]對Au線和Au/Ni/Cu材料的超聲波點焊進行二維和三維仿真，基于材料的應變率和硬化特性，模擬出了結合區域的應力應變分布，根據仿真結果對接頭處的強度受摩擦熱量的影響進行了分析，結果表明，摩擦熱量是主導接頭形成的因素。

2) 金屬箔材的塑性變形對溫度的影響。文獻[7]使用有限元仿真軟件建立了固接界面的模型，分析了金屬塑性變形狀態，結果表明，超聲振動使得金屬晶格受剪切應力作用發生滑移，其產生的摩擦熱增大局部金屬的塑性變形程度并釋放更多的熱量。文獻[8]在忽略了工具頭和底座對加工區域的熱量傳遞與滑動影響，且僅有與工具頭表面凸起相接觸的上層材料受到靜壓力等作用的前提下，對整個固結區域的溫度場進行了模擬，結果表明，在固結區域的適當的溫度提高和應變場作用下，金屬晶格在空穴內的擴散形成了金屬間的連接。

3) 固結工藝參數對溫度的影響。Elangovan 等[9]建立了三維的超聲固結系統熱-力耦合場的模型，研究系統中的復雜應力包括正應力和切應力、產生的熱量、塑性變形及之間的互相影響作用，從而發現了固結工藝參數對固結界面溫度的影響。

筆者針對超聲固結系統復雜的發熱問題，根據Hertz接觸理論和Coulomb摩擦定律分析了超聲固結區域的摩擦功，建立了固結區域處的發熱模型；基于超聲固結接頭處的主要熱源分布，通過有限元模擬來建立三維的超聲固結熱傳導模型；通過用熱電偶測溫實驗，驗證了該模型能較好的反映超聲固結接頭處的溫度變化趨勢。本研究內容將為超聲固結增材制造的加工工藝參數的優化提供指導。

1 理論分析

1.1 熱傳導

在進行溫度場數值仿真之前，由于在超聲固結過程中，熱的傳遞具有瞬時性與局部集中性等特點，這樣使得箔材的溫度變化不均勻，而且大量的熱量會在極短的時間內傳遞到箔材上，導致超聲固結過程的傳熱過程比一般的焊接傳熱過程要復雜，因此進行了如下假設：a. 應力分布均勻； b.假設加工工具頭是剛性物體，忽略其變形；c.假設工具頭與箔材之間無相對運動，只有箔材之間或者箔材與基板之間有相對運動；d.材料塑性變形發熱和摩擦力做功引起溫度變化。

在4個假設的前提下，筆者分析的超聲固結帶狀金屬箔加工的溫度模擬是非線性瞬態熱傳遞的過程模擬。由此可知在單位時間內，單元體中傳遞的熱量可由式(2)計算[10]

(1)

單元體的溫度總方程為

(2)

其中：ρ為材料密度；c為材料比熱容；?T/?t為隨時間變化的溫度變化率；q為材料內部變形產生的熱量；kx，ky，kz為熱傳遞系數，當固結材料為各向同性時，則熱傳遞系數kx，ky，kz相等。

計算式(2)時首先要給定該微分方程的初值和邊界條件。在超聲固結過程中，由于有加熱板提供加熱，所以基板和待加工箔材的初始溫度均為80℃，由于工具頭和固結箔材接觸面積較小，所以初始溫度定為室溫20℃。超聲固結過程中的傳熱是比較復雜的傳熱過程，涉及到輻射、對流以及傳導3種傳熱方式。在設定超聲固結過程中溫度分布的邊界條件時，分析為以下3種。

1) 剛性溫度邊界條件：已知某些結構邊界的溫度且為定值，這些溫度邊界條件為

Ts=T(x，y，z，t)

(3)

2) 輻射對流邊界條件：已知的結構和材料之間通過其他介質發生的輻射與對流，這類條件為

(4)

3) 熱流密度邊界條件：已知某種結構和材料的熱流密度分布，這類條件為

(5)

其中：α為材料表面傳熱系數；Ta為介質的溫度；Ts為剛性溫度條件；qs(x，y，z，t)為熱流密度函數。

1．2 熱源

超聲固結過程中由于界面間高速摩擦產生的摩擦功[5，9，11]為

(6)

其中：工具頭的平均振動速度vavg=4YΩ；Y為工具頭振幅；Ω為工具頭振動頻率；FFR為摩擦力；AFR為摩擦區域面積。

超聲固結過程中由于材料塑性變形產生的黏塑性變形熱[12]可由下式計算

(7)

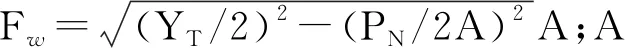
1.3 摩擦力應力分析

在超聲固結過程中，工具頭的高頻振動在整個固結系統的正壓力作用下帶動上層金屬箔，與下層箔材產生劇烈摩擦，并在兩箔材之間產生大量熱量。由于其施加的正壓力以及箔材粗糙度的不同，其產生的熱量導致溫度的變化也不一樣[13]。為了建立有效的溫度場分析模型，筆者利用Hertz接觸理論和Coulomb摩擦定律建立摩擦接觸模型，在小變形前提下，固結區域處的分布壓力在圓柱體與平面的接觸面上按拋物線分布，其數值可以通過Hertz接觸理論計算。當圓柱體與平面產生相對滑移時，兩者接觸面上切向力s的大小與分布滿足Coulomb摩擦定律。在建立接觸面上的法向變形方程時，由于工具頭硬度高，沿圓柱軸向產生的彈性滑動非常微小，為了簡化計算提高求解效率，筆者忽略了軸向彈性滑動引起的切向力[14-16]，直接計算圓柱面與平面之間產生滑動接觸時彈性體內應力場。將工具頭和箔材之間的滑動摩擦接觸簡化成圓柱和平面的滑動接觸，簡化成如圖1所示的平面應變問題。工具頭受一個向下的正壓力F作用并沿著平面滾動，金屬箔材保持靜止。工具頭與金屬箔材之間存在相對運動并有相互作用的分布切向摩擦力Q。

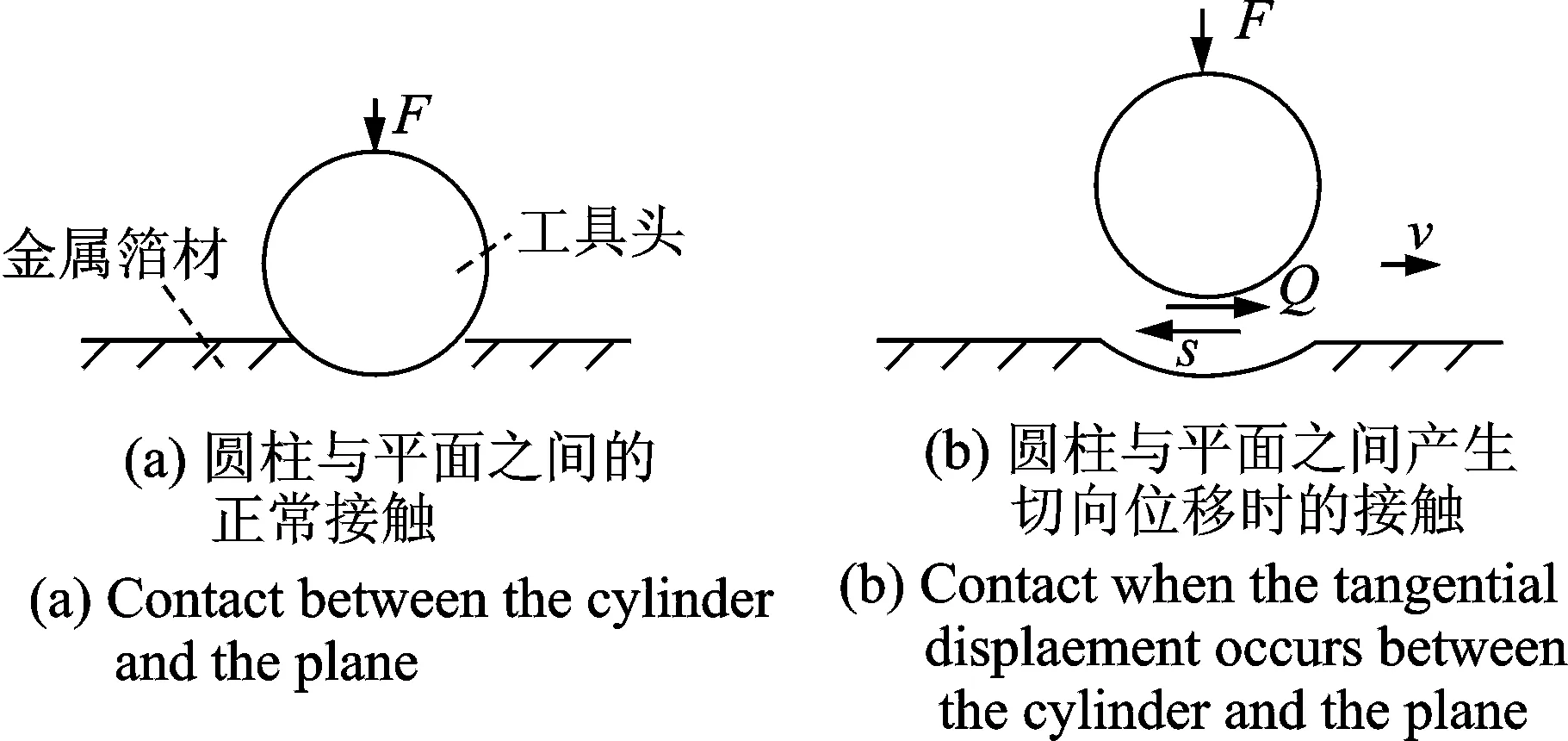
圖1 工具頭和金屬箔材之間的摩擦接觸模型Fig．1 Friction contact model between tool head and metal foil

2 有限元法數值仿真

2．1 模型介紹

在超聲波固結加工過程中，熱源主要來自于金屬箔材的塑性變形及金屬箔材間的高頻振動摩擦所生成的熱量，主要分布在位于工具頭下方的固結界面及其邊緣的區域。因此在建模過程中，將把金屬箔材的塑性變形生成的熱量和金屬箔材間的高頻振動摩擦生成的熱量分開來加載，前者加載到工具頭下方的塑性變形區域，后者加載到工具頭附近的界面摩擦區域。

加工工具頭使用的是粉末高速合金鋼，第1層箔材為鋁箔，第2層箔材為鈦箔。對于應力仿真分析，需要定義材料的密度、彈性模量及泊松比，如表1所示。

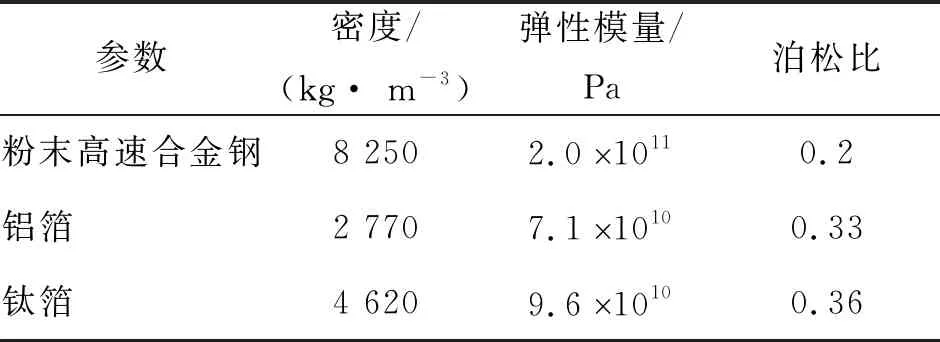
表1 材料屬性

設定仿真計算模型的初始條件:聲極振動幅值為20～60μm，振動頻率為20kHz，法向壓力為1.0kN～3.0kN。

超聲固結加工過程，工具頭受法向壓力加載在箔材上進行高頻振動，同時延z軸方向向前滾動，與箔材基本固定。由于相對于高頻振動產生的熱量，工具頭滾動過程對溫度場仿真影響較小，所以不添加工具頭軸向轉動條件。添加邊界條件如下：a.沿工具頭與箔材接觸區域分散出去的熱流量；b.金屬箔材的上表面和實驗時常溫空氣(20℃)的對流換熱系數為12 W/m2；c.下基板左右側面及底面為絕熱邊界條件，初始溫度為80℃；d.下基板與金屬箔材間的熱傳導系數設為12W/(m·℃)。

使用Ansys的workbench功能在固結區域輸入熱流密度，選用不同的工藝參數組合，仿真計算超聲固結鋁箔界面的溫度范圍。

2．2 模擬數值結果分析

不同固結時刻，金屬鋁箔表面不同點處的溫度值總體上呈現加工區域溫度最高，往兩側溫度逐漸降低的過程。筆者模擬了瞬態下某一時刻溫度場在超聲固結系統中的分布，在實際情況下隨著工具頭的移動，整個加工表面的最高溫度所在位置會隨著工具頭的移動而逐步向前推進。表面的最高溫度出現在工具頭移動到該位置處的時刻，并且在短時間內鋁箔表面溫度由初始溫度迅速上升到最高溫度。

選取20 kHz振動頻率作為定量條件，選用定量法向力與不同振幅和定量振幅與不同法向力條件，運用仿真模型得到在不同法向力和振幅條件下的溫度分布云圖以及溫度最高值。根據得到沿加工區域中心線散布到兩側各點的溫度值，獲得不同法向力沿固結方向溫度的分布規律。圖2為簡化后的超聲固結系統在20kHz振動頻率、40μm振動幅值、1.0kN固結壓力條件下模擬出的某一瞬態的溫度分布圖。從圖中可以看出，固結系統溫度的最高值為125.86℃，主要集中在工具頭和箔材以及箔材和基板接觸的區域，隨著進給方向兩側逐漸降低，逐漸降低到加熱板之前加熱到的溫度。

圖3為在20kHz振動頻率、40μm振動幅值及1.0kN固結壓力條件下模擬出的箔材邊界上沿固結方向的溫度分布。可以看出，在下基板上的最高溫度相對于圖2的整個超聲固結系統的最高溫度要稍低。在40μm振動幅值、1.0kN固結壓力條件下，下基板的最高溫度為115.86℃。

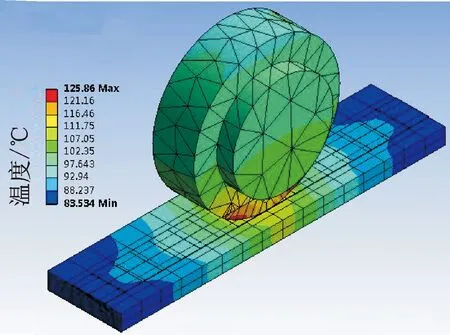
圖2 40μm振動幅值，1.0kN固結壓力下的溫度分布Fig．2 Temperature distribution at 1.0kN consolidation pressure and 40μm vibration amplitude

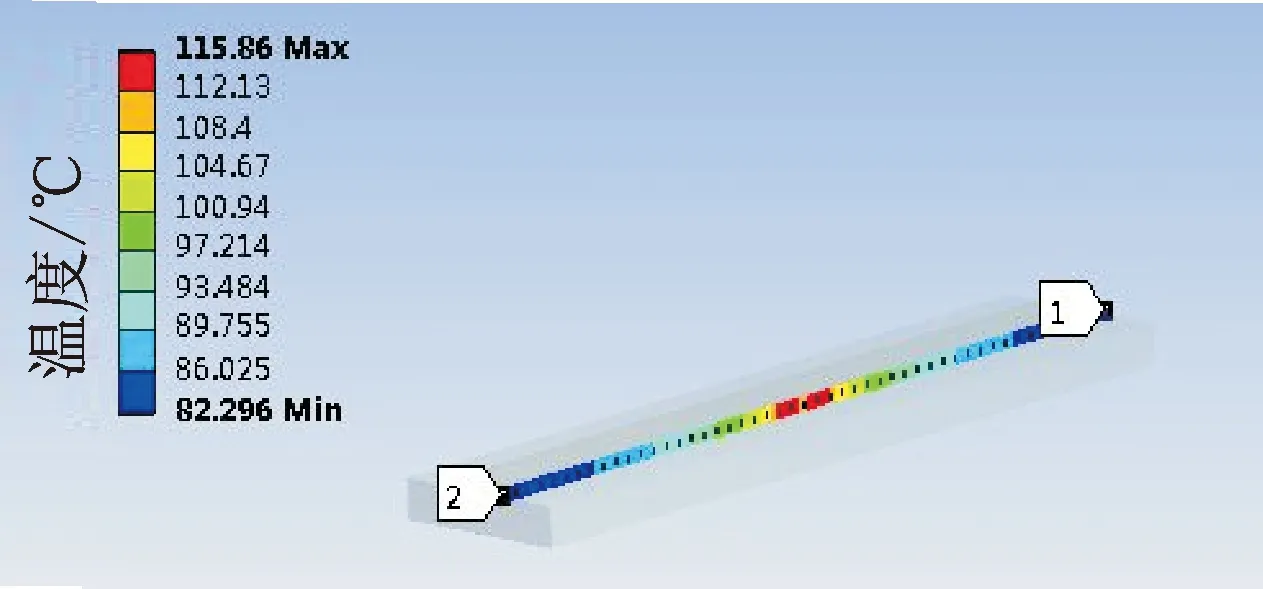
圖3 箔材邊界上的沿固結方向的溫度分布Fig．3 Temperature distribution along the consolidation direction at the foil boundary

3 熱電偶測溫實驗研究

3．1 實驗器材和裝置

實驗材料使用的是鈦合金帶狀金屬箔，寬度為24mm，厚度為0.2mm，調節CX-UAM-1型金屬超聲波固結裝置的參數，設置頻率為20kHz，進給速度為35mm/s，固結壓力和振子振幅根據仿真分析的設定數值進行調節。測量儀器選取的鎳鉻-鎳硅熱電偶即K型細絲熱電偶，以及日本SHIMADEN FP21型程序溫控器。

由于要測量的是固結界面接頭處的溫度變化，所以通過在距離基板上表面2mm處開一小孔，將K型熱電偶埋入小孔中并進行焊合。測溫時將箔材通過壓緊裝置直接壓在熱電偶所處的位置，工具頭加工進給過程中，溫控器能夠記錄當工具頭進給到熱電偶位置處時溫度的變化以及溫度的最大值。實驗所用的K型熱電偶的埋置位置如圖4所示。

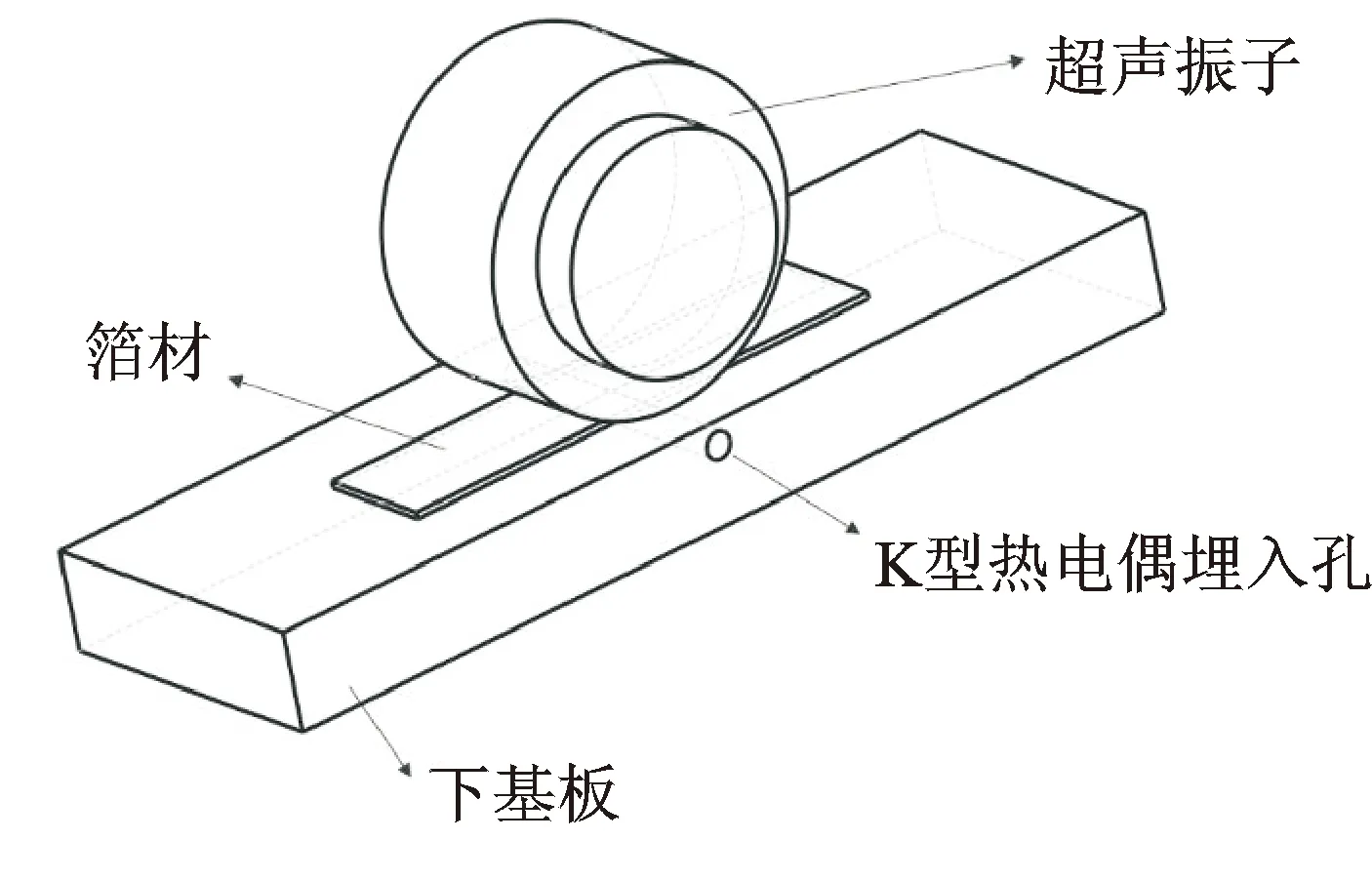
圖4 K型熱電偶的埋置位置Fig．4 Location of the K-type thermocouple

由于研究中的超聲固結加工不是常溫加工，需要等到加熱板加熱到一定溫度才能開始，而且熱電偶本身的熱慣性，要等一段時間直到測試端熱量出入達到動態平衡后讀數才準確。為了提高測溫實驗的效率，只將加熱板加熱到80℃，然后開始加工。實驗中除了熱電偶本身測溫的誤差外，由于將熱電偶埋置在下基板中，而該系統中主要的熱量來自箔材和基材的摩擦、箔材的塑性變形，所以箔材上的加工位置才應該是溫度場的真實值。相對于真實值，測量值可能稍有偏低[17-19]。

3．2 測溫結果和模擬數值的對比與分析

圖5為超聲固接系統在加熱到80℃后，20kHz振動頻率，40μm振動幅值，2.0kN固接壓力條件下的溫度測試平臺。可見，當工具頭加工進給到熱電偶位置時，溫控器顯示的溫度值為170℃，隨后逐漸降低到80℃的初始值。

圖5 40μm振動幅值，2.0kN固接壓力條件下溫度測試平臺Fig．5 Temperature test platform under 2.0kN fixed pressure and 40μm vibration amplitude

圖6為在20kHz振動頻率，40μm振動幅值條件下的固結界面最高溫度的實測值和模擬值隨著固結壓力變化的對比曲線。可見，模擬的最高溫度值和實測值還是有些偏差，在1.0kN固結壓力時，整個固結系統的最高溫度模擬值為125℃，而實測值僅為110℃，相差接近14%。由于測溫實驗的熱電偶是埋置在下基板中的，測量結果可能不是固結區域處的最高溫度，將此參數下的實測值和下基板最高溫度的模擬值115℃對比，發現僅相差4%左右，可見模擬結果還是較為準確的[20-21]。可以看出，隨著固結壓力的提高，固結界面的最高溫度逐漸提高，但是提升的幅度逐漸減小。

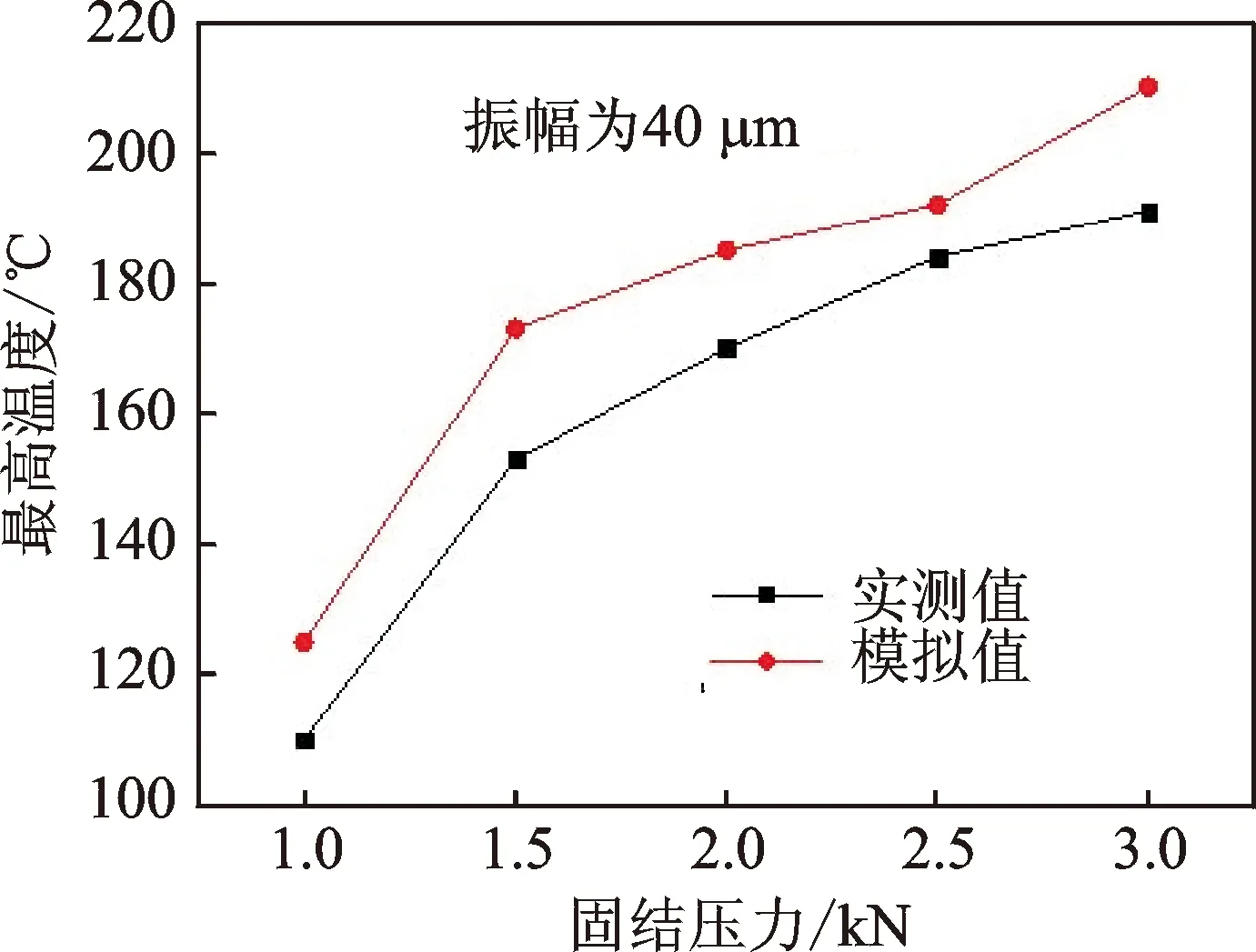
圖6 固結界面最高溫度值隨固結壓力的變化曲線對比Fig.6 Comparison of the maximum temperature value of the consolidation interface with the consolidation pressure

圖7為在20kHz振動頻率、2.0kN固結壓力條件下的固結界面最高溫度的實測值和模擬值隨著振子振幅變化的對比曲線。可見，在20μm振子振幅條件下的實測值與模擬值近乎相等，但是由于實測值是下基板的最高溫度值，所以真實的固結界面的溫度值還要稍高于145℃ 。隨著振子振幅逐漸提高，固結界面的溫度逐漸提高，且增長趨勢隨著振子振幅的提高越來越大。

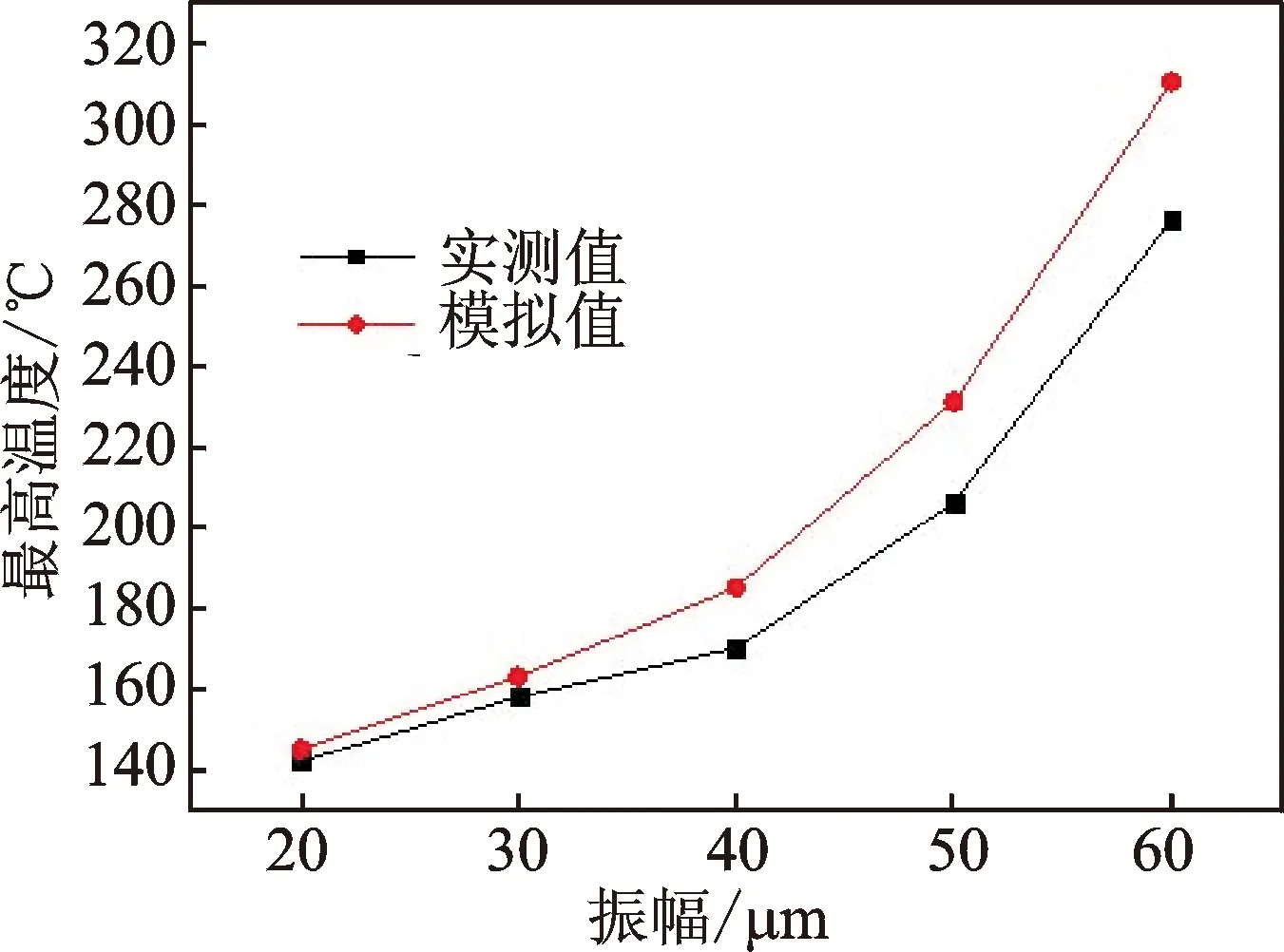
圖7 固結界面最高溫度值隨振子振幅的變化曲線對比Fig.7 Comparison of the maximum temperature value of the consolidation interface with the amplitude of the oscillator

4 結束語

根據Hertz接觸理論和Coulomb摩擦定律，分析了超聲固結區域的摩擦功，建立了對應區域的發熱模型。通過有限元模擬方法建立了三維超聲固結接頭處的熱傳導模型，使用熱電偶測溫的方法測量了下基板的實際溫度分布，并與模擬值進行了對比。結果表明，固結系統溫度的最高值主要集中在工具頭和箔材以及箔材和基板接觸的區域，隨著進給方向兩側逐漸降低，逐漸降低到加熱板之前加熱到的溫度；下基板上的實測最高溫度相對于的整個超聲固結區域處的最高溫度要稍低。實測結果與模擬的固結界面處的最高溫度值對比，發現僅相差4%左右，數值仿真模型能夠反映固結區域處溫度變化趨勢，從而得出整個超聲固結系統的最高溫度分布。