新課標(biāo)高考中導(dǎo)數(shù)內(nèi)容常考題型拙見

胡彩云

(廣西馬山縣馬山中學(xué) 530600)

我們都知道在高中階段，導(dǎo)數(shù)已成為研究函數(shù)性質(zhì)的一種重要工具,尤其是利用導(dǎo)數(shù)探討函數(shù)的單調(diào)性來解決相關(guān)的函數(shù)極值、最值、含參數(shù)以及不等式等問題，一直是高考命題的一大熱點.現(xiàn)將常考的題型做一個小歸納.

一、導(dǎo)數(shù)的概念及其幾何意義

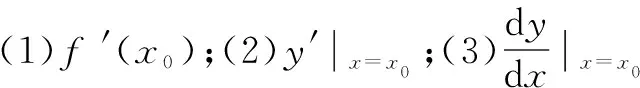
函數(shù)y=f(x)在點x0處的導(dǎo)數(shù)f′(x0)的幾何意義是在曲線y=f(x)上點(x0,f(x0))處的切線的斜率．相應(yīng)地，切線方程為y-y0=f′(x0)(x-x0)．

導(dǎo)數(shù)的幾何意義是每年高考的必考內(nèi)容，考查題型既有選擇題、填空題，也常出現(xiàn)在解答題的第(1)問中，難度偏小，屬中、低檔題．常見的命題角度有：(1)求切線方程；(2)求切點坐標(biāo)；(3)根據(jù)參數(shù)切線的性質(zhì)求參數(shù)．

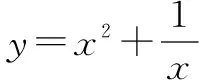
(2)已知直線l為曲線f(x)=x3+x-16的切線，且經(jīng)過原點，則它們的切點坐標(biāo)為____.

(3)若曲線y=f(x)=lnx+ax2(a為常數(shù))不存在斜率為負(fù)數(shù)的切線，則實數(shù)a的取值范圍是( ).

C．(0，+∞) D．[0，+∞)

二、求函數(shù)的單調(diào)性或用單調(diào)性解決簡單的極值最值問題

這類問題要求考生會正確掌握求導(dǎo)公式和求導(dǎo)法則，理解并掌握用導(dǎo)數(shù)判斷函數(shù)單調(diào)性的方法以及求極值、最值的方法步驟.函數(shù)的極值(最值)是每年高考的必考內(nèi)容，題型既有選擇題、填空題，也有解答題，難度適中，為中、高檔題．常見的命題角度有：(1)知圖判斷函數(shù)極值(最值)；(2)已知函數(shù)求極值(最值)；(3)已知函數(shù)極值(最值)情況求參數(shù)值(范圍)．而所有這些問題的解決，都依賴于用導(dǎo)數(shù)研究函數(shù)的單調(diào)性.其相關(guān)結(jié)論是：若f(x)函數(shù)在區(qū)間(a，b)上可導(dǎo),則在區(qū)間(a，b)上f(x)遞增?f′(x)≥0；f(x)遞減?f′(x)≤0.

例2 (1)函數(shù)f(x)=x+lnx的單調(diào)遞增區(qū)間為____.

(2)(2017課標(biāo)2，理11)若x=-2是函數(shù)f(x)=(x2+ax-1)ex-1的極值點，則f(x)的極小值為( ).

A.-1 B.-2e-3C.5e-3D.1

(3)(2017課標(biāo)3，理11)已知函數(shù)f(x)=x2-2x+a(ex-1+e-x+1)有唯一零點，則a=____.

三、利用導(dǎo)數(shù)解決不等式的證明問題

利用導(dǎo)數(shù)研究函數(shù)單調(diào)性來證明不等式 ，在高考的壓軸題中是最常見的也是難度較大的問題.在證明的過程中，需綜合考慮不等式相關(guān)的特點，然后通過恒等變形不等式或構(gòu)造出函數(shù)，接著利用導(dǎo)數(shù)證明構(gòu)造出的函數(shù)的單調(diào)性達(dá)到證明不等式的目的.常見的有：一是直接構(gòu)造函數(shù),然后用導(dǎo)數(shù)證明該函數(shù)的增減性；二是先把不等式變形后再構(gòu)造函數(shù),然后利用導(dǎo)數(shù)證明該函數(shù)的單調(diào)性,達(dá)到證明不等式的目的.三是轉(zhuǎn)化為用導(dǎo)數(shù)求函數(shù)的最值來證明不等式.

例3 證明：當(dāng)x>0時，x-ln(1+x)>0.

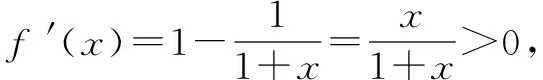
故有f(x)>f(0)=0即x-ln(1+x)>0.

例4 證明：當(dāng)x>0時，x>sinx.

分析先把不等式變形為x-sinx>0，就轉(zhuǎn)化為例3類的問題，用同樣的方法即可證明.

例5 證明：當(dāng)x≠0時，ex-x>1.

證明設(shè)f(x)=ex-x-1(x≠0)，則f′(x)=ex-1.

令f′(x)=0得到x=0，且當(dāng)x<0時，f′(x)<0;當(dāng)x>0時，f′(x)>0;

所以f(x)在(-∞,0)上單調(diào)遞減，在(0,+∞)上單調(diào)遞增.x=0為極小值點，也是最小值點.即f(x)>f(0)=0，ex-x>1.

當(dāng)然，在利用導(dǎo)數(shù)證明不等式問題中，還有一類難度較大的題型，那就是構(gòu)造函數(shù)，證明數(shù)列不等式問題，在這里就不做闡述和舉例.

四、不等式恒成立問題的處理方式

所謂不等式恒成立，其實就是指函數(shù)無論取最大值或最小值時不等式都能成立.通過證明不等式的恒成立問題，將其轉(zhuǎn)化成解決函數(shù)最值的問題，就可以利用其證明不等式是否成立.而要證明不等式的恒成立就會涉及參數(shù)的證明問題，通過變量分離，證明某個值大于或小于函數(shù)值，就可以證明不等式恒成立.也就是往往把變量分離后可以轉(zhuǎn)化為m>f(x) (或m

而解決這類問題的策略常有：

①首先要構(gòu)造函數(shù),利用導(dǎo)數(shù)研究函數(shù)的單調(diào)性,求出最值,進(jìn)而得出相應(yīng)的含參不等式,從而求出參數(shù)的取值范圍.

②分離變量,構(gòu)造函數(shù),直接把問題轉(zhuǎn)化為函數(shù)的最值問題.

當(dāng)然，在高中階段，導(dǎo)數(shù)相關(guān)的題型還有很多，比如存在性問題，實際應(yīng)用問題等等，高考考查的題目靈活多變，常考常新.雖然在2018年理科高考壓軸題中，考查不等式問題的難度稍有下降，但是還是會常考不衰.這類題目的解答過程中，教師應(yīng)引導(dǎo)學(xué)生選擇正確的切入點，構(gòu)建出不等式，只有這樣，才能準(zhǔn)確地利用導(dǎo)數(shù)知識證明不等式是否成立.因此，在實際的教學(xué)中，教師必須組織、引導(dǎo)學(xué)生學(xué)好導(dǎo)數(shù)的知識，不僅為高考考一個好分?jǐn)?shù)，更要為日后的學(xué)習(xí)微積分知識奠定堅實的基礎(chǔ).