數學方法在物理平衡中的應用

王天煬 指導教師：李慶林

(山東省肥城市泰西中學 271600)

物體的平衡在物理學中有著廣泛的應用，歷年來高考中經常出現.在解決平衡問題時用到的數學知識很多，下面列舉幾例說明.

一、函數解析法

利用函數解析法解題，要求寫出所求物理量的表達式，然后根據表達式分析求解.

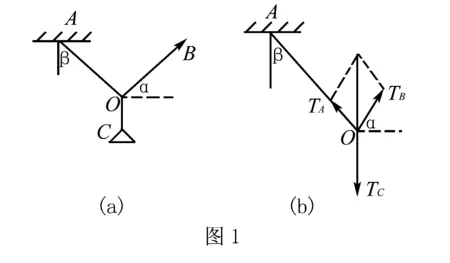
例1 一盞電燈重為G，懸于天花板上A點在電線O處系一細繩OB，使電線OA與豎直方向的夾角為β=30°，如圖1(a)所示，現保持β角不變，緩慢調整OB方向至OB線上拉力最小為止，此時OB與水平方向夾角α等于多少？OB繩中的最小拉力為多大？

解析在電線OA、OB、OC的拉力TA、TB、TC作用下，結點O處于平衡狀態，電燈亦處于平衡狀態.結點O受力圖如圖1(b)，根據三力平衡特點，任意兩個力的合力一定與第三個力等值反向，故TA、TB的合力F=TC=G.根據正弦定理有：TB/sinβ=F/sin(90°+α-β)=G/sin(90°+α-β)，所以TB=Gsin/cos(β-α).

由此式可以看出，當sin(90°+α-β)=1,即α=β=30°時，TB最小，且TB=Gsinβ=G/2.

二、圖象法

圖象貫穿于整個高中物理學習中，它把抽象、隱含的物理問題還原成形象、直觀的物理模型，利用圖象可以將復雜的物理過程簡捷化.

例2 如圖2(a)所示，質量為m的球放在傾角為α的光滑斜面上，試分析檔板AO與斜面間的傾角β多大時，AO所受壓力最小？

解析根據牛頓第三定律，擋板對小球的壓力等于小球對擋板的壓力.故把小球作為研究對象.小球受到的重力產生兩個作用效果，一是對斜面有擠壓，一是對擋板有擠壓，根據作用效果，將重力進行分解，其兩個分力為F1、F2，如圖2(b)所示.

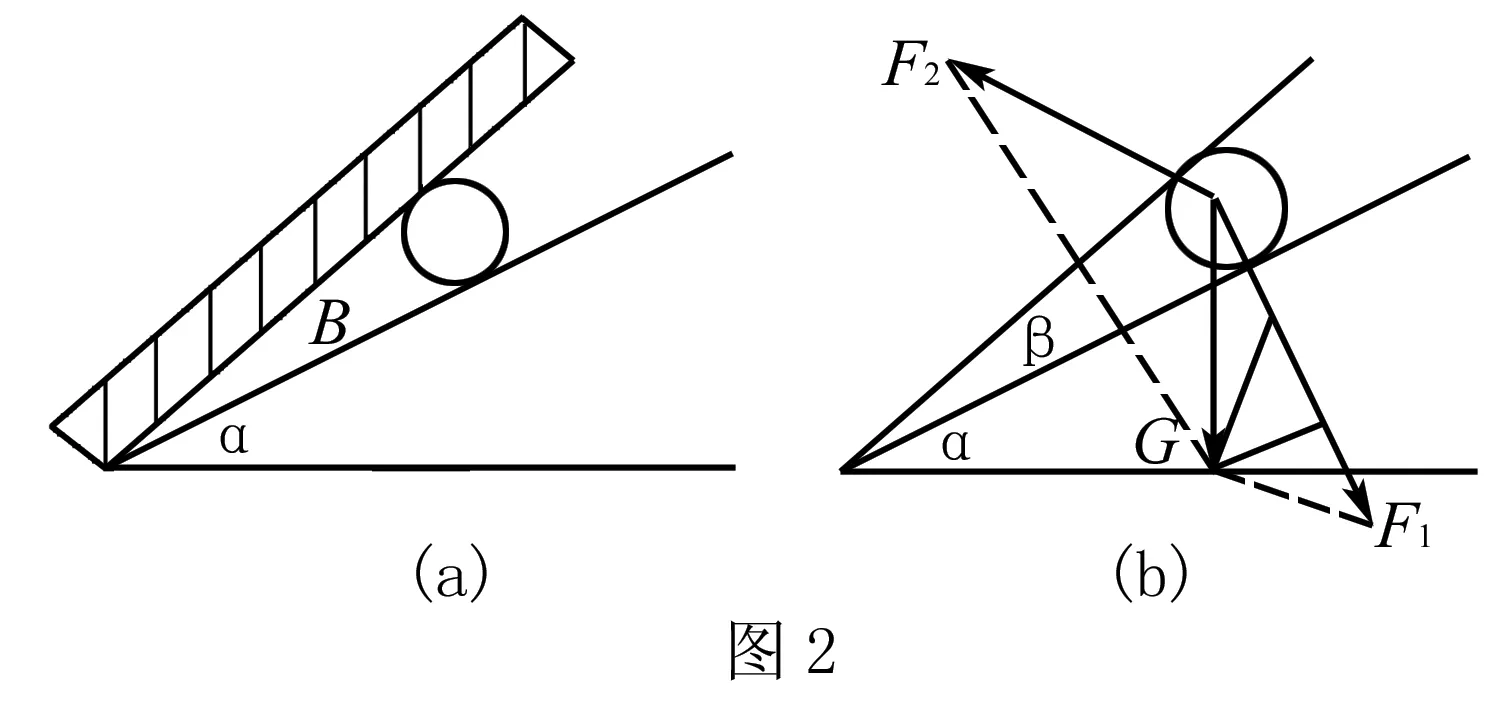
重力和兩個分力構成矢量三角形，如圖.在這個三角形中重力大小、方向保持不變，F1的方向保持不變，隨著F2的方向變化，其大小和F1的大小不斷發生變化，但始終和重力構成三角形，故從變化的圖中可以看出，F1不斷變小，F2先變小后變大，當F1和F2垂直時，F2具有最小值.即β=90°時，擋板所受壓力最小.且最小壓力F2min=mgsinα.

三、三角形相似法

三角形相似法是找出邊三角形和相應的力三角形，根據相似三角形的知識解決問題的一種方法.

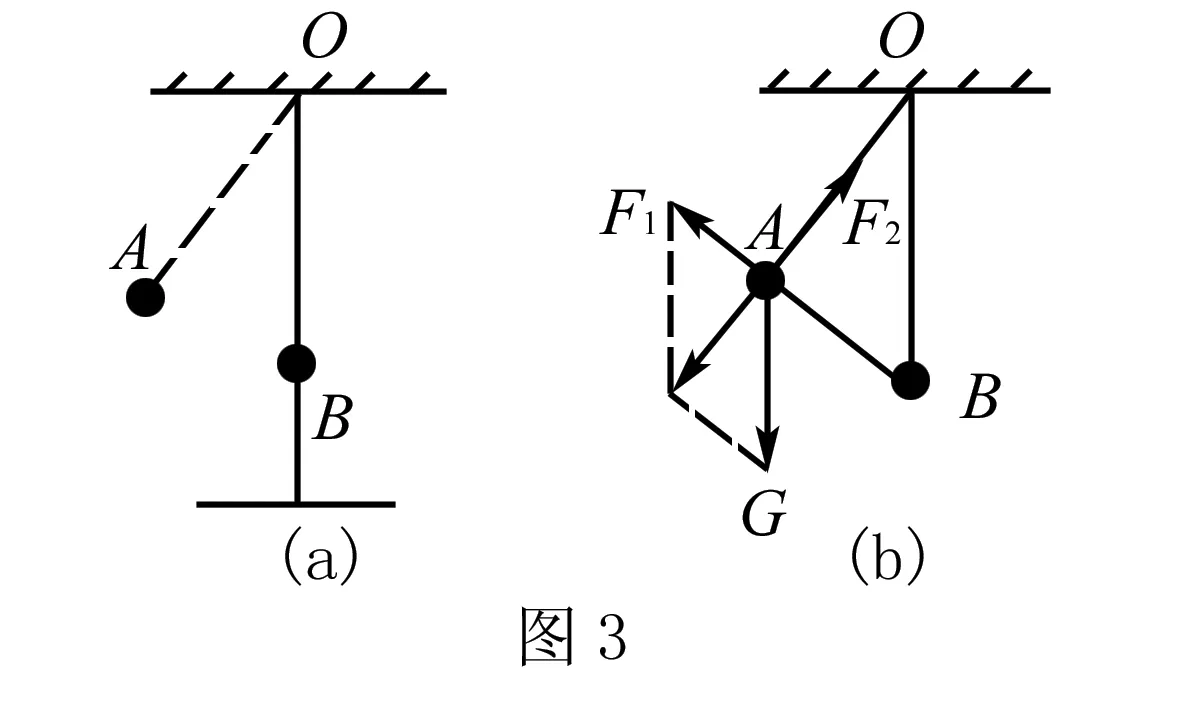
例3 如圖3(a)，空氣中有兩個帶電小球A和B，B被長為l的絕緣細線懸于固定點O，且被絕緣支架固定于O點的正下方，與O點的距離也為l,與A球相距d1，由于漏電，過一段時間后，A的帶電量變為原來的4/9，B的帶電量變為原來的2/3，試求此時A、B兩球間的距離.

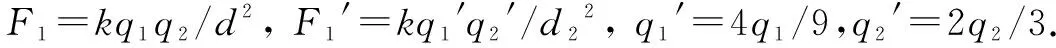
帶入上式得d1/d2=3/2

即d2=2d1/3

四、極限法

極限法是物理中常用的一種方法，一般情況下先寫出所求物理量的表達式，再根據數學方法求極值，把比較隱蔽的臨界現象挖掘出來.

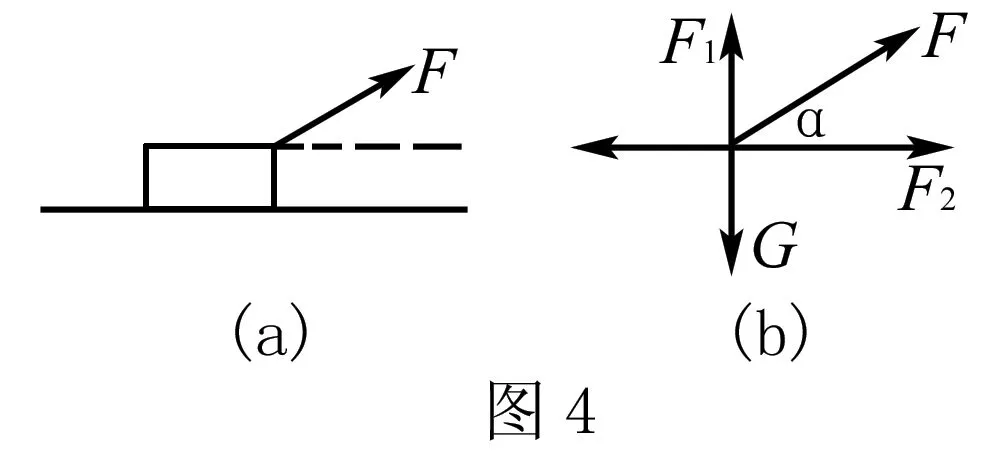
例4 木箱重為G，與地面的動摩擦因素為μ，用斜向上的力F拉木箱使之沿水平地面勻速前進，如圖4(a)，問角α為何值時拉力F最小，這個最小值是多少？

解析對木箱進行受力分析，重力G、支持力F1、拉力F、摩擦力F2如圖4(b).根據平衡條件有：

水平方向：Fcosα=F2=μF1,

豎直方向：F1+Fsinα=G

由上兩式得Fcosα+μFsinα=μG

F=μG/(μsinα+cosα)

令μ=tanβ

帶入得F=Gtanβ/(tanβ+cosα)=Gsinβ/cos(β-α)

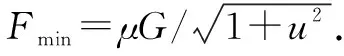
從以上例子可以看出，我們在物理教學和學習中，要打破學科之間的界限，加強學科之間的滲透，這樣有利于培養學生綜合運用知識的能力.