等差數(shù)列前n項(xiàng)和公式的拓寬及應(yīng)用

卜佳文

(河北省唐山市第二中學(xué) 063000)

求和問題是數(shù)列中的重點(diǎn)和難點(diǎn)，對(duì)于等差數(shù)列的前n項(xiàng)和Sn來說，可以進(jìn)一步將其拓寬，從而得到很好的結(jié)論，這樣更有利于我們進(jìn)一步加深對(duì)它的理解、掌握和運(yùn)用.

結(jié)論1 在等差數(shù)列{an}中，前n項(xiàng)和為Sn，公差為d，k∈N*.則S2k=k(ak+ak+1)，S2k+1=(2k+1)ak+1.

證明：當(dāng)n=2k時(shí)，a1+a2k=a2+a2k-1=…=ak+ak+1，所以Sn=k(ak+ak+1)；

當(dāng)n=2k+1時(shí)，a1+a2k+1=a2+a2k=…=ak+ak+2=2ak+1，所以Sn=(2k+1)ak+1.

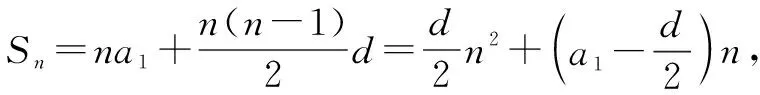
所以Sm=Am2+Bm，Sn=An2+Bn，

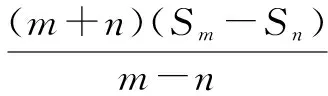
=A(m+n)2+B(m+n)=Sm+n，

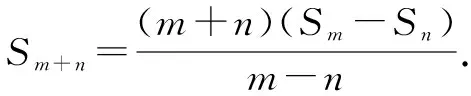
同理可證：Sm+n=Sm+Sn+mnd.

推論1 在等差數(shù)列{an}中，前n項(xiàng)和為Sn，m、n∈N*，m≠n，若Sm=n，Sn=m，則Sm+n=-(m+n).

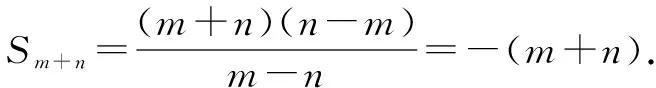
推論2 在等差數(shù)列{an}中，前n項(xiàng)和為Sn，m、n∈N*，m≠n，若Sm=Sn，則有Sm+n=0.

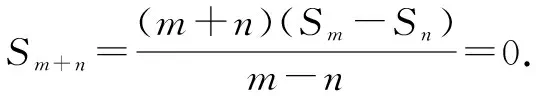
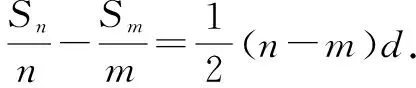
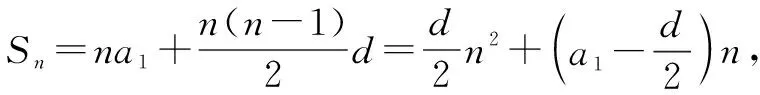
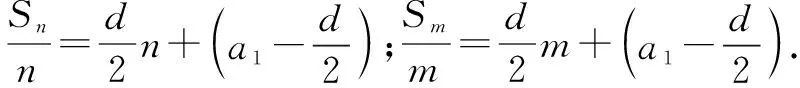
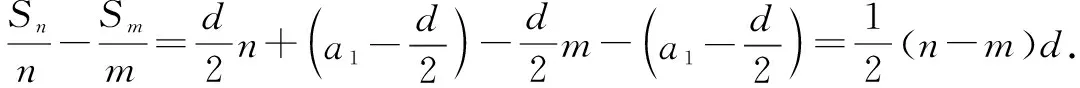
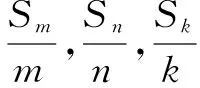
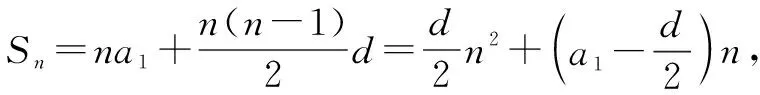
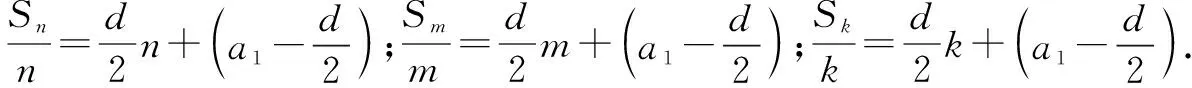
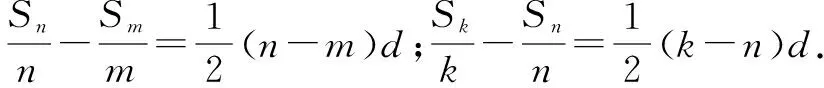
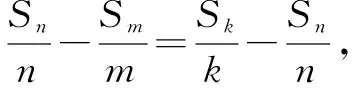
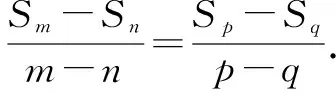
證明：

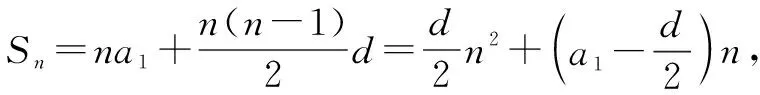
所以Sp=Ap2+Bp，Sq=Aqn2+Bq，Sm=Am2+Bm，Sm=Am2+Bm.

∵p+q=m+n，

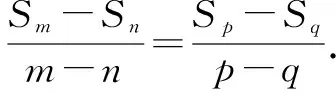
應(yīng)用舉例練習(xí)：

1.在等差數(shù)列{an}中，若a6+a9+a12+a15=20，求S20.

2.等差數(shù)列{an}的前10項(xiàng)的和為150， 其中項(xiàng)數(shù)為奇數(shù)的各項(xiàng)和為120，求第六項(xiàng).

3.一等差數(shù)列的前10項(xiàng)之和為100，前100項(xiàng)的和為10，則前110項(xiàng)的和為( ).

A.-90 B.90 C.-110 D. 110

4.等差數(shù)列{an}的前m項(xiàng)和為30，前2m項(xiàng)和為100，則它的前3m項(xiàng)和為( ).

A.130 B.170 C.210 D.260

5.如果等差數(shù)列{an}的前4項(xiàng)和是2，前9項(xiàng)和是-6，求其前n項(xiàng)的和Sn.

6.已知數(shù)列{an}是等差數(shù)列，Sn是其前n項(xiàng)和，設(shè)k∈N*，Sk，S2k-Sk，S3k-S2k成等差數(shù)列嗎？