發動機推力對大展弦比機翼顫振邊界的影響

聶雪媛,余明亮,鐘培楠,楊國偉

(中國科學院力學研究所流固耦合系統力學重點實驗室,100190,北京)

翼吊式發動機的氣動布局在當前民用飛機中得到了廣泛應用[1],但這種布局使得發動機和機體之間會存在干擾。在飛行過程中,發動機推力會改變機翼的穩定性,即使推力本身的大小不足以引起機翼的失穩,但其與氣動載荷和機翼彈性運動的耦合作用仍會改變機翼的顫振邊界。現代飛行器的設計越來越追求輕質,使得機翼結構的柔性日趨增大,機翼的變形加劇,發動機推力和質量效應對機翼顫振速度的影響更為顯著。因此,研究發動機推力對柔性機翼穩定性的影響,對于飛行器的設計意義匪淺。

發動機的推力相對于機翼來說,屬于橫向載荷,具有典型的隨動特征,會對結構的振動模態和頻率產生重要影響。Como最早研究了在自由端施加的橫向隨動力對彈性懸臂梁彎扭穩定性的影響,得到了臨界隨動力的解析解[2]。Feldt等考慮了隨動力加載點處的質量,探討了在翼尖隨動力作用下機翼的氣動彈性穩定性問題,指出橫向隨動力對氣動彈性系統具有不穩定作用,而增加集中質量可提高系統穩定性[3]。Hodge等以機翼的彎扭剛度比作為參數,分析了柔性機翼的顫振特性,但沒有考慮外掛的質量[4]。Fazelzadeh等研究了發動機質量、推力及其作用位置等參數變化對顫振邊界的影響,指出不可忽視外掛質量對顫振邊界的影響[5]。此外,張健等在文獻[5]的基礎上,進一步討論了機翼后掠角和上反角的影響[6];陳全龍等分析了推力大小和作用位置對顫振速度的影響,指出了發動機推力效應在顫振分析中的重要性[7];王鋼林等研究了機翼在不同攻角下的定常氣動力與發動機推力聯合作用下結構的固有振動和顫振特性,結果表明發動機推力可能成為大型運輸機機翼設計的限制因素[8]。

目前已有的考慮發動機推力對機翼氣動彈性穩定性影響的研究中,結構建模多采用基于有限元的線性梁模型或Hodges幾何精確完全本征梁模型[9],氣動力主要通過Peters有限狀態模型、Theodorsen氣動模型或者面元法等進行計算。當前,計算流體力學(CFD)技術已經廣泛應用于流固耦合力學問題的研究,CFD-CSD(計算結構動力學)方法已成為當前進行非線性氣動彈性分析可信度最高的方法[10-11],而如何采用CFD-CSD耦合方法進行考慮發動機推力影響的氣動彈性穩定性分析,國內外尚未見到相關報道。

本文發展了一種基于Simo幾何精確梁模型和雷諾平均Navier-Stokes方程的氣動力耦合計算方法。首先以文獻[12]中的流固耦合算法標模——帶柔性懸臂梁的方柱繞流為算例,驗證了該方法的準確性;然后以大展弦比機翼為研究對象,采用橫向隨動力和集中質量模擬發動機推力和外掛質量,分析機翼的彎扭剛度比、外掛點安裝位置、外掛質量、發動機推力等參數的變化對機翼穩定性的影響規律。

1 CFD-CSD耦合計算方法

數值計算方法采用氣動結構耦合的時域分析方法,將流體控制方程和結構動力學方程相耦合,進行考慮結構彈性變形的氣動彈性求解。流固耦合問題通常包括流場運動、結構動力學以及在兩者交界面處的數據交換,其基本方程和邊界條件可表示為

(1)

S(u)=E(Q,x)

(2)

x=H(u) onΓ

(3)

式(1)為流場控制方程,其中Q(x,t)是式(1)基于歐拉坐標的解向量,F和Fv分別是無黏和黏性通量;式(2)為結構動力學方程,其中u是結構節點位移,E是作用在結構節點上的外部氣動載荷;式(3)描述了流固耦合界面的連續性條件,其中H是結構位移到流場位移的插值算子,Γ是流固耦合界面。

1.1 結構模型

Hodges幾何精確本征梁[13]是當前研究梁的幾何非線性效應常用的方法,該方法在梁的幾何變形上沒有采取任何近似,利用速度和應變獨立描述結構狀態。在理論推導方面同樣沒有采取任何近似的是Simo幾何精確梁[14],它完全采用微分幾何語言描述張量、截面轉動和應變度量等物理量,具有明晰確定的幾何意義[15]。考慮到Simo理論在數學描述上的優勢,本文嘗試采用基于Simo幾何精確梁理論發展起來的幾何精確梁模型對大展弦比機翼進行結構有限元建模,以期為當前梁結構的建模方法提供更多的選擇。

該幾何精確梁模型將結構的運動分為兩部分,一是梁中心軸線的任意運動,一是梁橫截面的有限轉動,并以此來描述梁的任意大變形。梁在運動過程中除了受到彎曲、扭轉和拉伸變形外,還受到剪切變形的作用。幾何精確梁的示意圖如圖1所示。

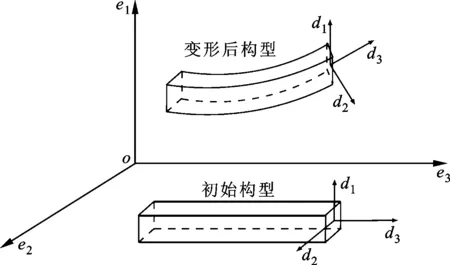
圖1 幾何精確梁示意圖

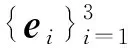
di=Λei

(4)

式中轉動矩陣Λ滿足ΛΛT=ΛTΛ=I3,|Λ|=1。

該模型的動力學方程可描述如下

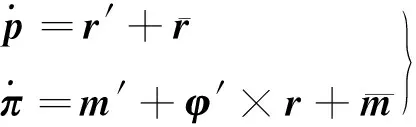
(5)

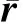
對動力平衡方程(5)不能直接使用有限元方法離散,需要通過虛功原理得到平衡方程的變分形式。對于給定的構型Φ=(φ,Λ)(φ為梁的軸線位置),允許的虛位移ζ=(η,ν),其中η為軸線的小位移,ν為橫截面上的小轉動。將這2個小量點乘式(5),并在梁的長度區間[0,L]上積分,最終得到

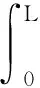
(6)

式中?ΦΦ為Dirichlet邊界,有

根據虛功類型不同,可將上式各項分為外力虛功Wext、內力虛功Wint及慣性虛功Wdyn,分別對應式(6)中各項,可寫為

Wdyn+Wint=Wext

(7)

用一帶集中質量Me的隨動力來描述發動機對大展弦比機翼的推力,梁結構在隨動力作用下需要考慮隨動載荷對其模態帶來的影響。

作用在梁結構某節點上的隨動力可以表示為

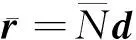
(8)

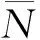
隨動力的引入會改變結構的剛度矩陣,同時,隨動力加載點處的附加質量也會改變結構的質量矩陣。通過推導隨動力所做的虛功[16],可得作用在節點上的隨動力切向載荷剛度

(9)

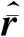
結構在外載荷作用下達到靜平衡位置時,其切向剛度

(10)

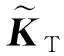
設靜平衡位置處的線化質量矩陣為MT,平衡位置處的模態振型φ和頻率ω可以通過下式的廣義特征值分析得到

(KT-ω2MT)φ=0

(11)

考慮發動機推力的結構平衡位置附近的小擾動動力學方程可寫為

(12)

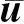
(13)

因此對式(13)在平衡位置進行線性化,可得

(14)

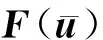
(15)

將其代入式(14)得

(16)

由于載荷剛度的加入,破壞了系統剛度矩陣的對稱性,式(11)計算出的特征向量之間并不正交,所以不能在方程(16)左右簡單乘以φT以轉換為廣義運動方程。將矩陣ψ作用于方程(16),該矩陣滿足

(17)

式中1N為N階單位矩陣,N為所取的結構模態階次。求解矩陣ψ其實就是尋找MTφ的廣義逆矩陣或偽逆矩陣,這可以通過奇異值分解的方法完成。最終得到結構的廣義運動方程為

(18)

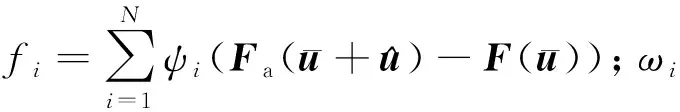
結構在不同隨動力作用下的平衡構型不同,從而使得結構的模態也隨之變化。因此,對于考慮發動機推力的機翼顫振計算,與線性顫振相比需要在結構靜變形平衡位置計算結構的模態,屬于非線性顫振計算。

綜上所述,考慮發動機推力作用的機翼顫振計算流程如圖2所示。

圖2 CFD-CSD非線性顫振計算流程

1.2 氣動控制方程

氣動力數值計算軟件采用自主開發的基于有限體積法的CFD求解器[17]。該求解器的控制方程為三維雷諾平均N-S控制方程。守恒型流動方程(1)的積分形式可表達為

(19)

式中:S為控制體V的邊界面積;n為面的法向量;t為物理時間。將式(19)按有限體積法進行空間離散,可得

(20)

式中:VI為第I個控制體單元的體積;NF為包圍第I個單元的所有面數;ΔSm為第m個表面的法向面積。

N-S方程組的空間離散分為無黏項和黏性項。黏性項的離散采用二階中心差分格式。無黏項是非線性對流的集中體現,離散采用Roe格式,即

(21)

式中:A為Roe矩陣;上角標R、L分別表示相關變量來自單元界面的右邊和左邊。

對式(20)采用二階三點近似,進行時間離散可得

(22)

式中RI為殘差,代表式(20)的右邊項。

為提高時間推進精度,在式(22)中引入虛擬時間,最終可得到以下時間離散形式

(23)

式中:上角標*表示虛擬時刻對應的物理量;l為虛擬時間步。在虛時間域上采用LU-SGS(lower-upper symmetric Gauss-Seidel)隱格式對氣動方程作隱式時間推進,當子迭代步l→∞時,Q*l→Qn+1即可求得流場在下一物理時間步的解。

該CFD數值仿真軟件已經在工程應用中得到了驗證[1,17-19]。

1.3 氣動-結構耦合

由于結構和氣動控制方程在數學模型和求解方法上的不同,難以實現兩者的統一求解,目前通用的方法是將結構和氣動獨立求解。由于在耦合界面上流場和結構網格具有不同的拓撲形式和分布密度,需要對2個子系統在界面上進行力和位移的交換。

用xf和us分別表示耦合界面上流場和結構網格的位移,λf和λs分別表示作用在界面上的流體載荷和結構載荷,耦合界面的運動必須滿足的2個條件為

(24)

為了保證界面總能量守恒,在界面上的數據交換必須要滿足虛功原理,即

(25)

式中δW為虛功。界面上流場網格點的位移可通過結構網格點的位移插值得到,即

xf=H·us

(26)

其中插值矩陣H由所采用的插值方法來確定,采用基于徑向基函數(RBF)的插值方法[19],以實現流固耦合界面的數據交換。將式(26)代入式(25),可得由界面氣動力載荷轉換得到的結構節點力

λs=HT·λf

(27)

流固耦合的迭代過程如圖3[20]所示。

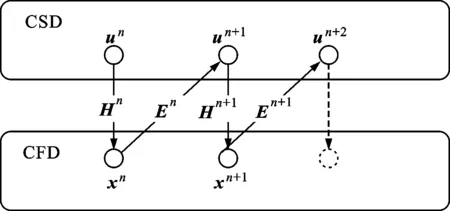
圖3 流固耦合計算的迭代過程

在計算得到流場結構交界面的氣動物面位移之后,就可以調用動網格變形技術進行整個流場空間網格的變形。采用并行RBF插值方法進行空間網格變形,具體過程可參見文獻[19]。

2 方法驗證

為驗證本文所采用的CFD耦合幾何精確梁方法的正確性,對浸沒在流場中帶有柔性懸臂梁的方柱進行結構響應分析,并與已有文獻的結果進行比較。該模型是驗證流固耦合算法的標模,模型參數詳見文獻[12]。柔性懸臂梁選用幾何精確梁作為結構模型,共用41個有限元節點離散,其計算流場如圖4所示。

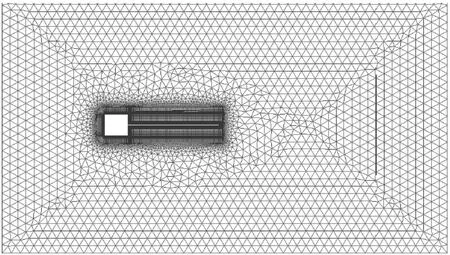
圖4 帶懸臂梁方柱的計算網格

流體經過方柱會產生渦脫落,引起柔性懸臂梁振動,其中自由端的振幅和振動頻率是諸多文獻作為判斷求解流固耦合算法是否準確的關鍵參數。采用本文方法計算出的自由端垂向位移和振動頻率如圖5所示。

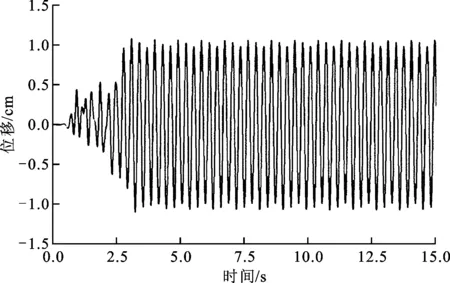
(a)自由端垂向位移時程

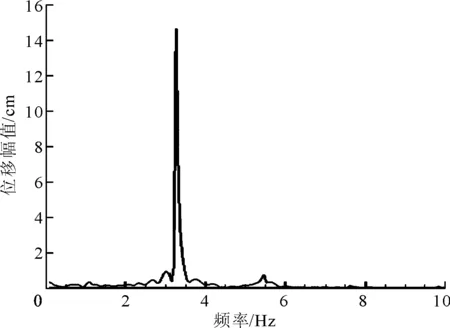
(b)自由端位移頻譜圖5 懸臂梁自由端垂向位移的計算結果

從圖5可以看出,自由端垂向位移平均幅值為1.05 cm,其主頻約為3.2 Hz。

表1給出了本文與已有文獻的計算結果比較,

表1 計算結果比較

可以看出本文方法得到的結果與其他文獻的結果吻合良好。

3 算例與分析

對本文方法進行驗證后,以文獻[4]中的大展弦比Hale機翼為研究對象,首先研究不考慮氣動力時發動機推力對機翼穩定性的影響,具體分析發動機的安裝位置、質量以及結構剛度比的作用,并在此基礎上探討上述各參數對大展弦比機翼氣動彈性穩定性的影響規律。

Hale機翼模型的結構參數和飛行條件見表2,其中弦向彎曲剛度遠大于展向彎曲剛度(EI3?EI2),γ為展向彎曲剛度與扭轉剛度之比。機翼采用梁模型描述,在發動機推力作用下的機翼示意圖如圖6所示。

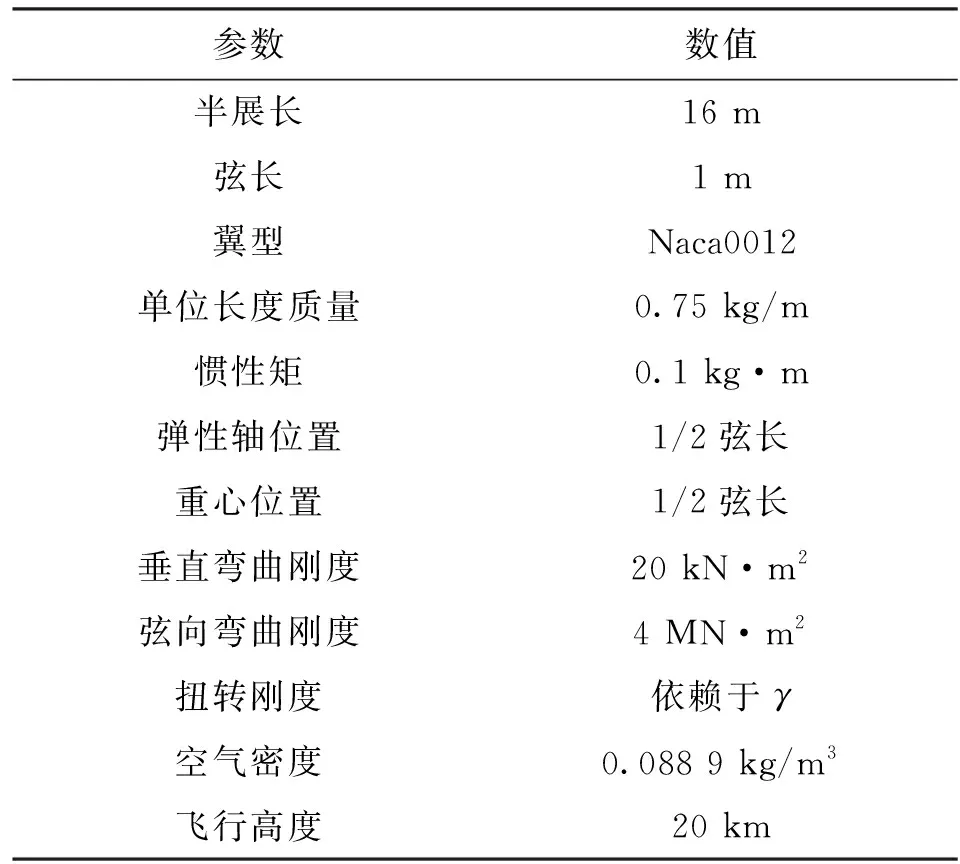
表2 Hale機翼模型的結構參數和飛行條件

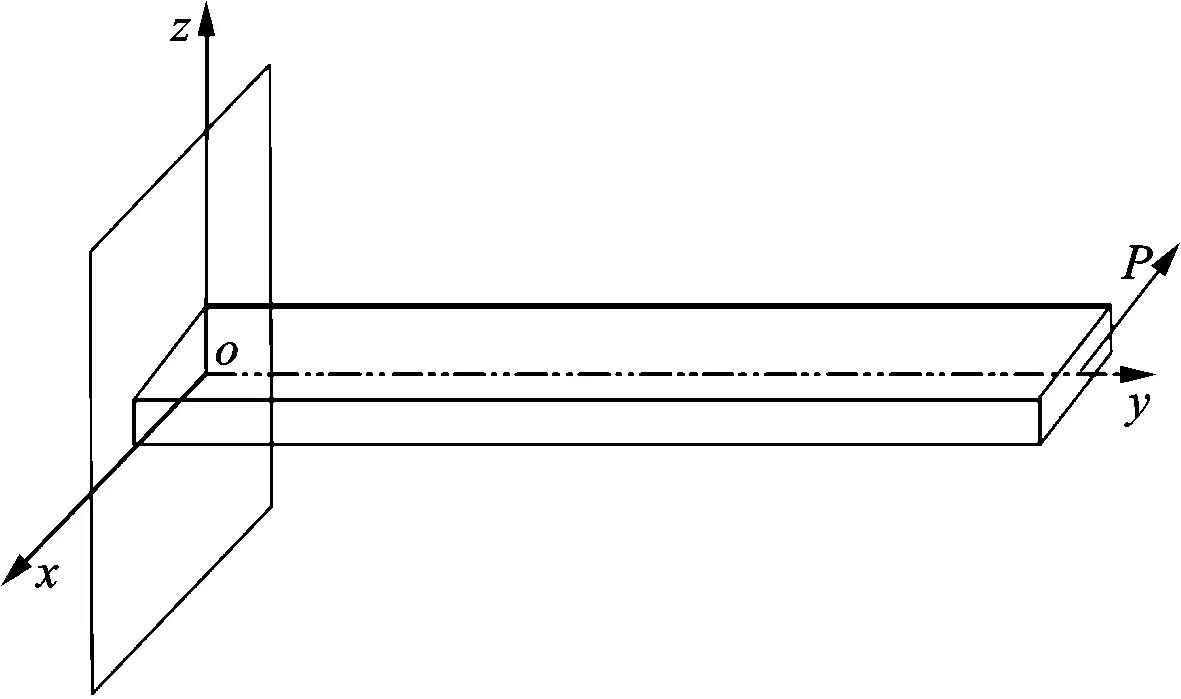
圖6 隨動力作用下的Hale機翼梁模型示意圖

采用本文1.1小節中基于Simo理論的幾何精確梁模型建立機翼的有限元模型,y軸對應于機翼的弾性軸,即幾何精確梁的中軸線,通過1/2弦長位置。采用30個有限單元進行計算;為進行界面耦合,在梁模型截面分布了6個離散點。圖7是建立的機翼幾何精確梁有限元模型,其中圓點代表有限元節點,正方形點代表用于流固耦合界面數據交換的結構網格點,亦即用于耦合界面進行位移和氣動力插值的結構節點。

(a)有限元模型俯視圖

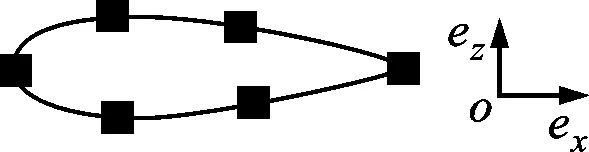
(b)梁模型橫截面圖7 Hale機翼有限元模型定義歸一化參數如下

(28)

式中:U為來流速度;ωT1為結構的第一階固有扭轉頻率;Ye為發動機位置到機翼根部的展向距離;Xe為相對于彈性軸的集中質量弦向位置(位于彈性軸的后方為正);b為1/2弦長;c為機翼弦長;Ma為機翼質量;Me為發動機集中質量。下文各圖中未標明單位的均為歸一化數據。

流場計算網格采用混合網格,為更好地刻畫邊界層內的流動,在壁面附近布置了邊界層網格。首層高度為機翼特征長度l的3×10-6倍,計算網格規模約為67萬,流場計算網格如圖8所示。湍流模型采用兩方程渦黏性模型——Wilcoxk-ω模型。

圖8 Hale流場計算網格

3.1 發動機推力對機翼結構模態的影響

3.1.1 發動機推力對結構模態的影響 計算中采用的模態為結構的前5階模態,包括4個彎曲模態和1個扭轉模態。用Vi代表第i階垂直彎曲模態,Hi代表第i階水平彎曲模態,Ti代表第i階扭轉模態。

首先,對本文的幾何精確梁模型進行方法驗證。給定梁的彎扭剛度比γ=2,在翼梢(即ye=1處)施加橫向隨動力P,在結構靜平衡位置處進行穩定性分析,即對式(11)進行特征值求解,得到系統的臨界推力為332.6 N,與文獻[4]中給出的335.1 N基本吻合,證明了基于Simo理論發展的幾何精確梁模型求解方法的有效性。

圖9給出了在γ=2、其他變參數為0的情況下,發動機臨界推力P隨發動機安裝位置ye的變化曲線,從中可以看出,發動機安裝點距離翼根越近,則其臨界推力越大。

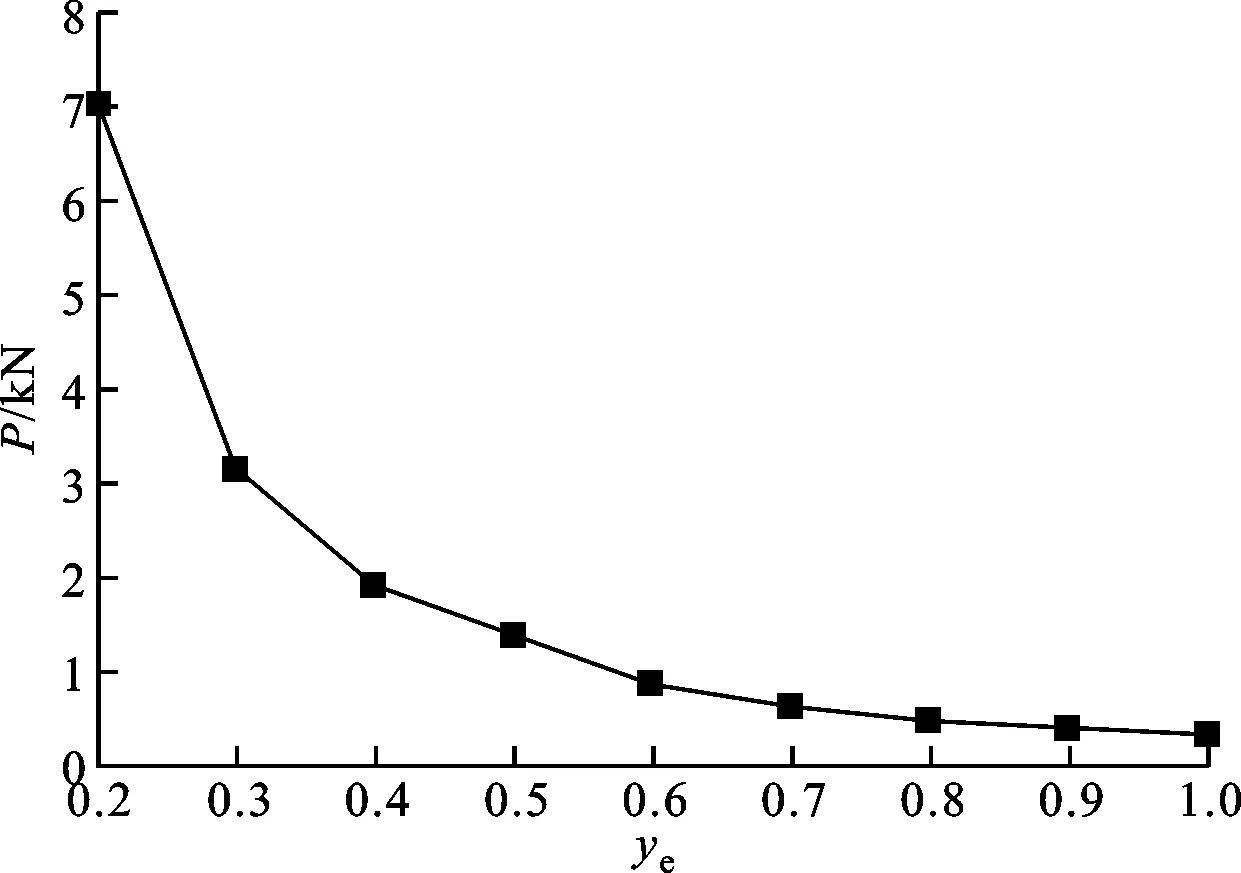
圖9 γ=2時結構不同位置的臨界推力

由于推力和結構的平衡位置均有所不同,使得系統質量矩陣和剛度矩陣發生改變,最終導致結構模態發生變化。

選定γ=2,ye=1,其他變參數為0,計算系統特征值(特征值的實部代表頻率,虛部代表阻尼)隨發動機推力的變化,結果如圖10所示。

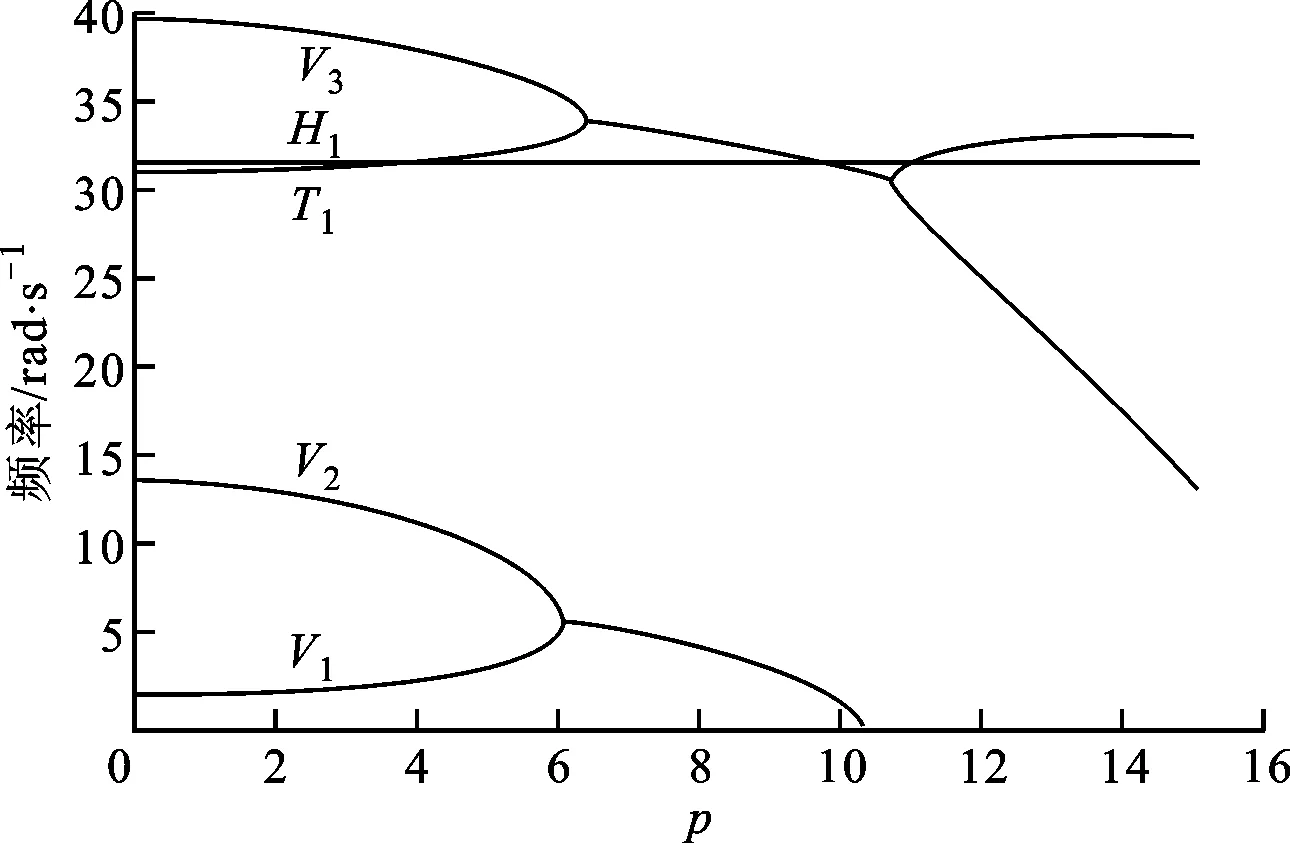
(a)機翼頻率隨推力的變化

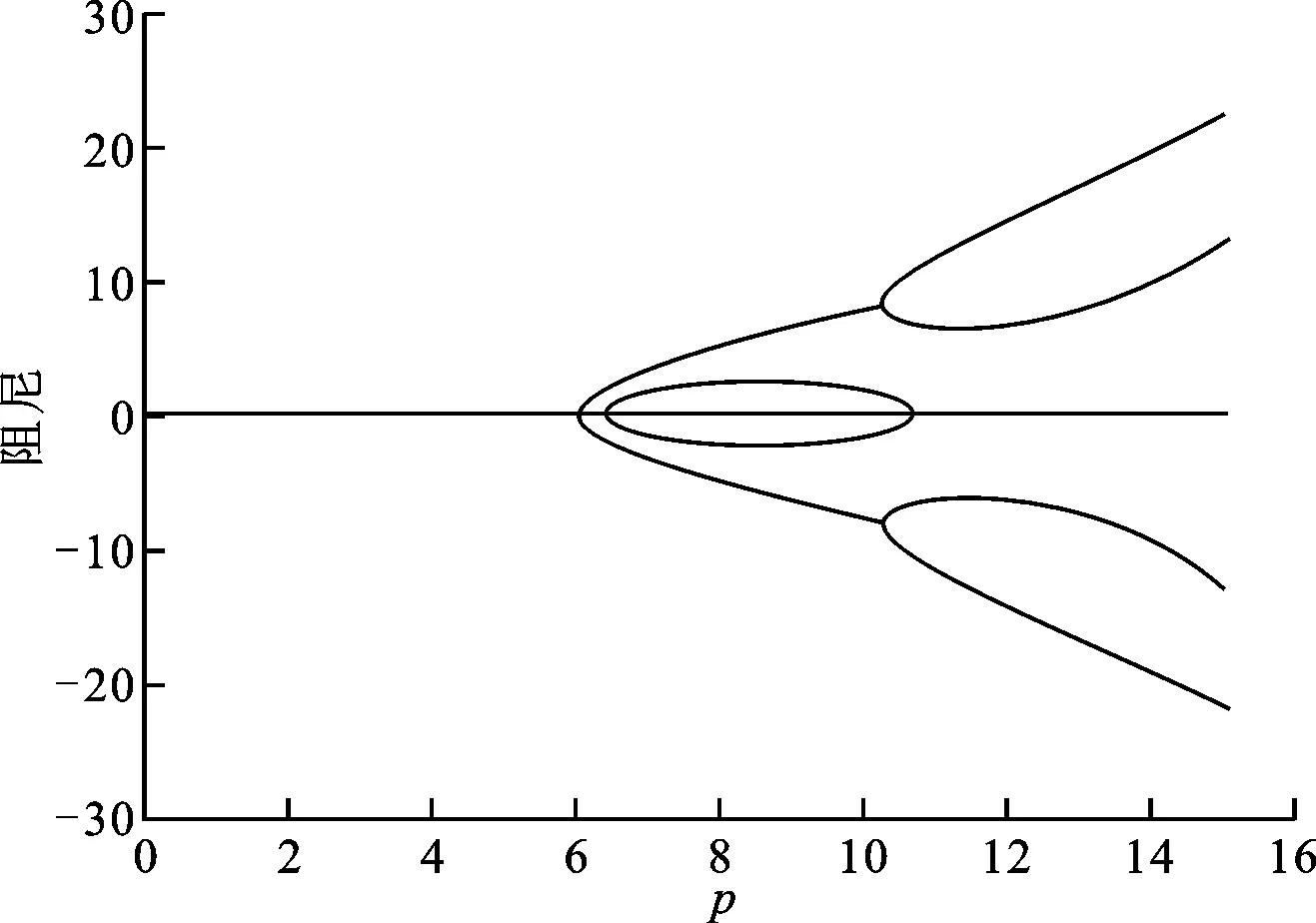
(b)阻尼隨推力的變化圖10 γ=2、ye=1時系統特征值隨推力的變化

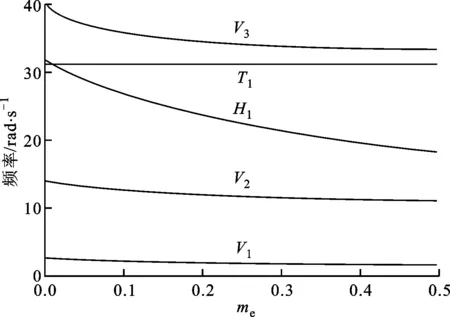
(a)p=0,xe=0

從圖10中可以看出:一階水平彎曲頻率H1不受推力的影響,其值基本保持不變;在臨界推力范圍內,一階垂直彎曲頻率V1和一階扭轉頻率T1隨著推力的增大而逐漸增大;二階垂直彎曲頻率V2和三階垂直彎曲頻率V3隨著推力的增大而減小;當推力超過臨界值(此處p=6.02)時,系統出現了復數特征值,一階和二階垂直彎曲對應的特征值最先形成一對共軛特征值,系統進入不穩定區域,該現象與文獻[4]中的情況相似。

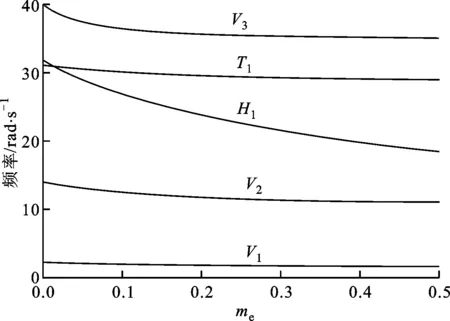
(b)p=0,xe=0.25圖11 γ=2、ye=1時機翼特征頻率隨 發動機集中質量的變化

3.1.2 發動機質量對結構模態的影響 為研究發動機質量效應對結構的影響,選取γ=2,ye=1,改變發動機的集中質量,分別計算發動機安裝在xe=0,0.25位置時,機翼的特征頻率隨發動機質量的變化,結果如圖11所示。

從圖11可以看出:當發動機安裝位置位于機翼端部時,除一階扭轉頻率T1外,結構各階頻率都隨著集中質量的增大呈現出下降趨勢;當發動機安裝的弦向位置位于彈性軸,即xe=0時,質量對彈性軸無轉動慣量,因此一階扭轉頻率T1不受集中質量變化的影響,隨著發動機弦向安裝位置遠離彈性軸,質量相對彈性軸產生轉動慣量,此時一階扭轉頻率T1隨集中質量的增大而逐漸減小。此外,發動機安裝在機翼彈性軸前后位置對結構模態的影響很小,這是因為在本算例中沒有考慮氣動載荷的影響,大展弦比機翼簡化為一個梁模型,彈性軸前后對稱,所以發動機前置或后置產生的差異并不大。

3.2 發動機推力對機翼氣動彈性穩定性的影響

顫振是氣動彈性領域中最危險的一類動不穩定現象。本小節從機翼顫振特性出發,研究發動機推力及其相關參數對結構氣動彈性穩定性的影響。

與求解線性結構顫振不同,由于發動機推力隨結構變形而變化的隨動特性,機翼的模態發生改變,因此在分析機翼的顫振特性時,需要首先對建立在考慮隨動載荷作用的靜平衡位置上的線性小擾動結構動力學方程進行模態分析,即實現對方程(16)的廣義模態求解。

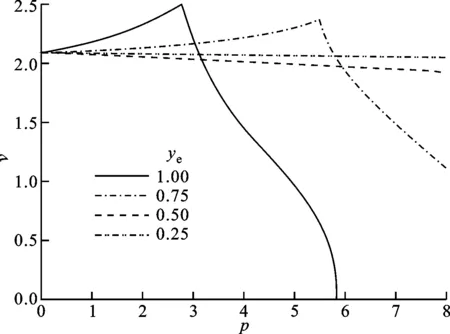
3.2.1 發動機推力及作用的展向位置對顫振邊界的影響 給定γ=2,me=0,xe=0,研究機翼顫振特性隨發動機推力及其作用在機翼不同展向位置的變化規律。展向位置ye=0.25,0.5,0.75,1處顫振邊界隨推力變化的計算結果如圖12a所示;在歸一化推力p=1,2,3,4時,機翼顫振速度隨推力作用的展向位置的變化見圖12b。

從圖12a可以看出,發動機的位置越靠近機翼根部,推力對顫振特性的影響就越小,這是因為柔性機翼的穩定性依賴于其變形狀態,而發動機推力作用越靠近翼根,其對機翼變形的影響就越小。此外,隨發動機推力向翼根靠近,穩定效應的范圍會不斷增大,因此,應盡量將發動機安裝在靠近機翼根部的位置。

(a)推力對顫振速度的影響

圖12b顯示,在推力較小(p=1,2)時,發動機安裝位置距離翼根越遠,機翼的顫振速度就越大;隨推力繼續增大(p=3,4),顫振邊界隨展向位置的變化趨勢發生改變,即隨著p的增大,推力的增穩效應逐漸減弱,這是因為誘發結構失穩的推力和氣動力耦合作用中所包含的不穩定效應增強的結果。

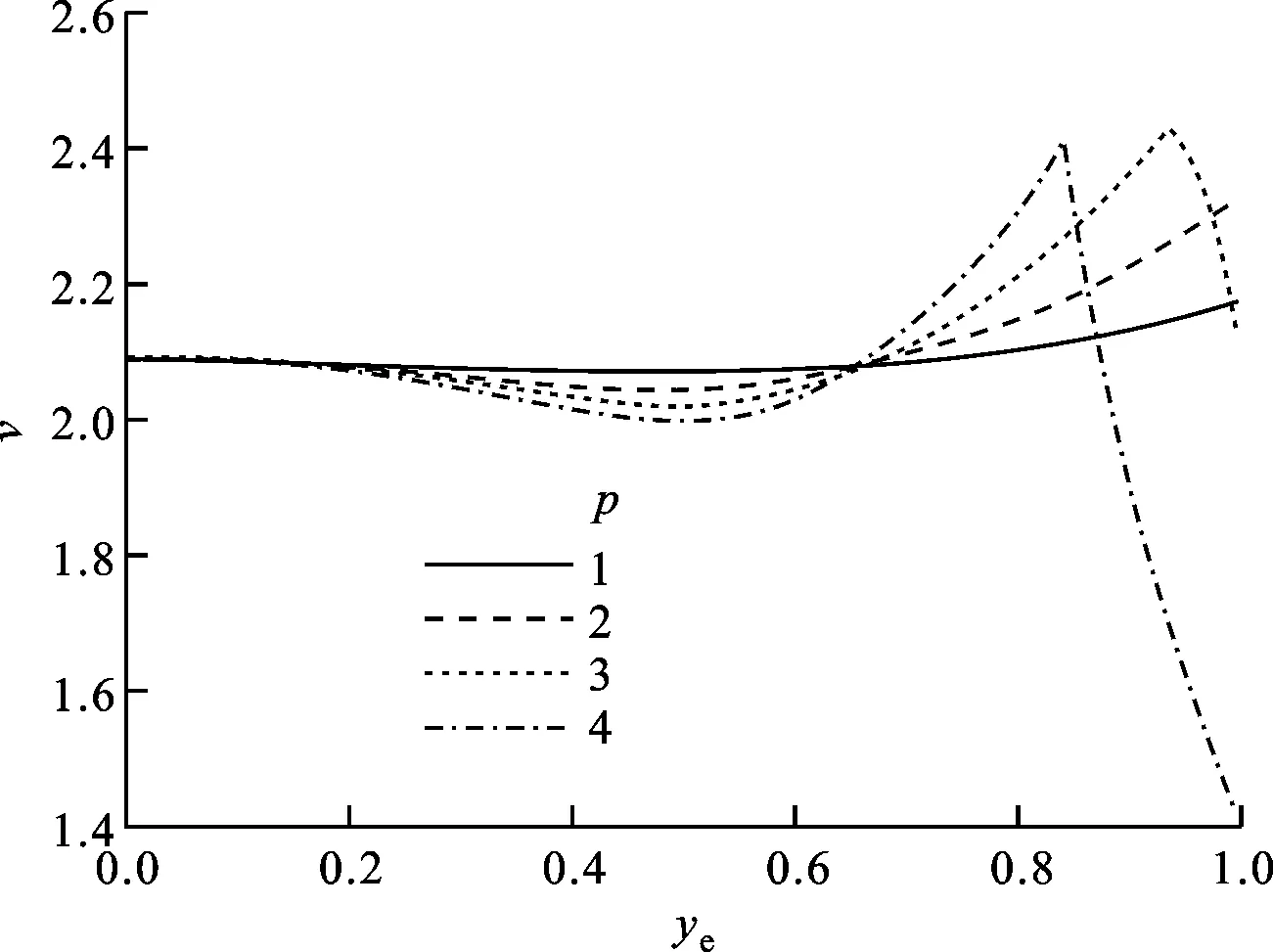
(b)展向位置對機翼顫振速度的影響圖12 γ=2、me=0、xe=0時發動機推力和 展向位置對機翼顫振速度的影響

注:發動機推力的增穩效應是指,隨著發動機推力的增加,機翼顫振速度隨之增大或基本保持不變的特性。

3.2.2 發動機的弦向位置對顫振邊界的影響 圖13所示為γ=2、ye=1時,給定發動機集中質量條件下不同弦向位置對機翼顫振邊界的影響。

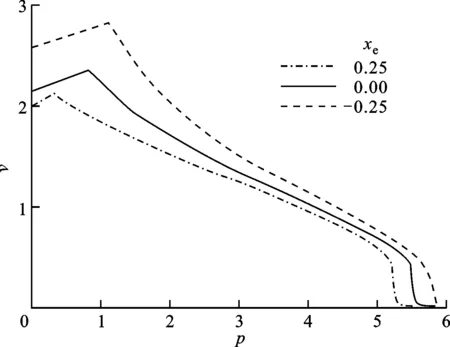
(a)γ=2,ye=1,me=0.2

集中質量弦向位置的變化不會導致發動機推力關于彈性軸產生附加力矩,因此圖13中各曲線之間的相互關系反映出集中質量的弦向位置變化對顫振特性的影響。從圖13可以看出,隨著集中質量從機翼后緣向前緣移動,顫振邊界不斷擴大,這是因為集中質量位于彈性軸之前有助于減小局部有效攻角,提高顫振速度。從圖13a可以看出,當me=0.2時,集中質量前置(xe由0.25到-0.25)使得機翼顫振速度變化曲線的拐點向右上方移動,發動機推力增穩效應的范圍增大。在圖13b中,對于較大的質量me=0.4,發動機后置時顫振速度變化曲線的拐點消失,可見發動機推力增穩效應的范圍也受集中質量弦向位置變化的影響。因此,安裝發動機時應該考慮將發動機安裝在機翼彈性軸之前,以提高系統的氣動穩定性。

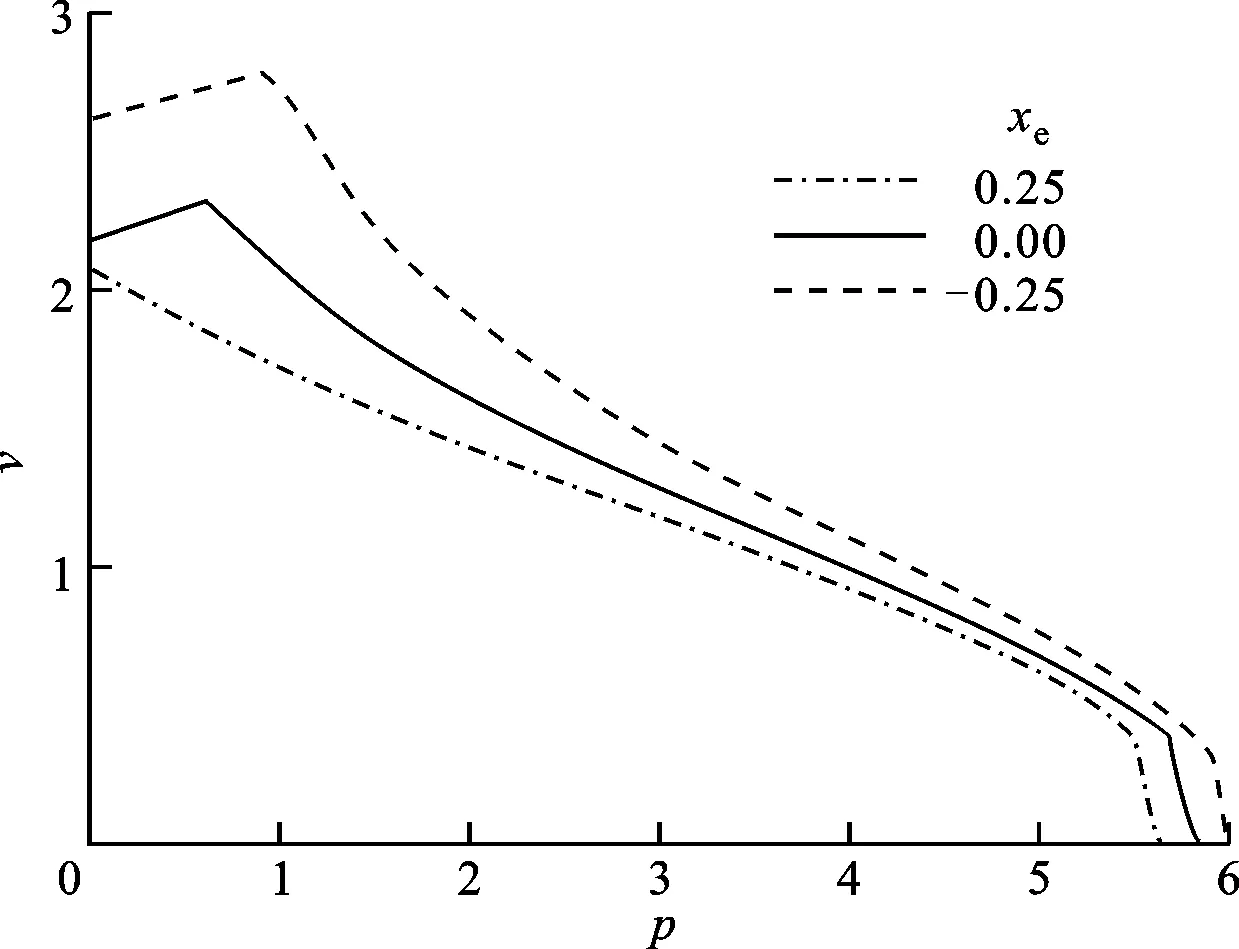
(b)γ=2,ye=1,me=0.4圖13 集中質量的弦向位置對顫振邊界的影響

3.2.3 發動機集中質量和推力對顫振邊界的影響給定γ=2,ye=1,xe=0,研究發動機推力及集中質量對機翼顫振邊界的影響。計算了當發動機歸一化集中質量me=0.1,0.2,0.3,0.4時推力對顫振速度的影響(結果見圖14a),以及歸一化推力p=1,2,3,4時機翼顫振速度隨集中質量的變化(結果見圖14b)。

圖14a的計算結果表明,柔性機翼的顫振速度以及發動機推力的穩定效應幾乎不受集中質量變化的影響,隨著發動機推力的增大,其增穩效應逐漸減弱,直至呈現出加速機翼失穩的作用(隨著發動機推力增大,顫振速度快速下降),這與圖12b的結果相似。

圖14b的結果顯示:隨著發動機推力的增加,機翼顫振速度隨集中質量的增大呈現下降趨勢;集中質量增大會降低機翼的氣動彈性穩定性,集中質量越大,機翼越容易發生顫振。

(a)顫振邊界隨推力的變化

3.2.4 彎扭剛度比對顫振邊界的影響 選取ye=1,γ=1,2,5,10,其他變參數為0,研究機翼顫振邊界隨推力的變化,結果如圖15所示。

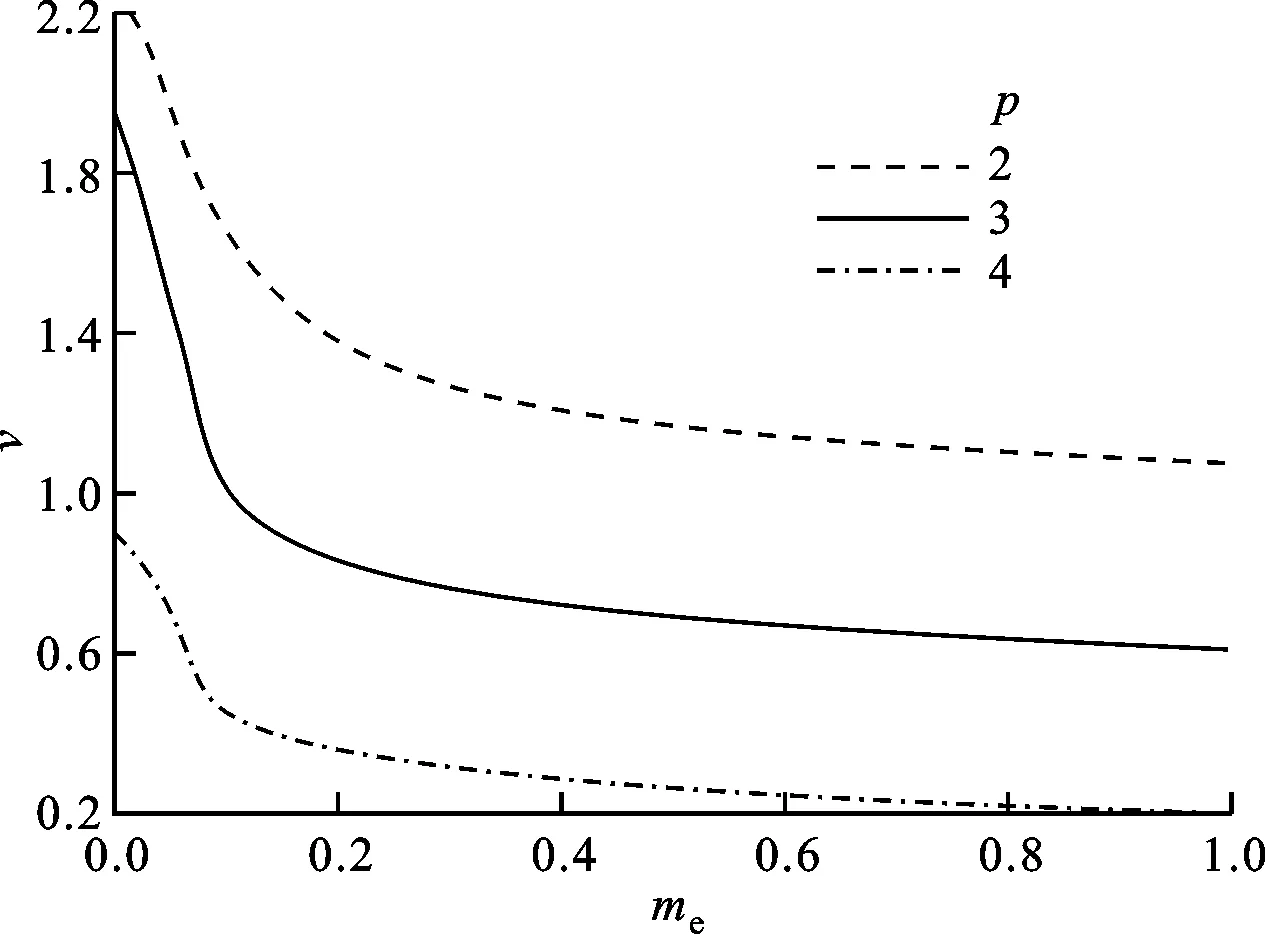
(b)顫振邊界隨集中質量的變化圖14 γ=2、ye=1、xe=0時集中質量和推力 對顫振邊界的影響

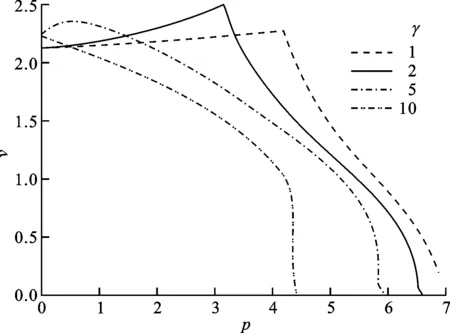
圖15 彎扭剛度比對顫振邊界的影響

由圖15可以看出,顫振速度隨推力的變化趨勢在γ=5時發生了改變,在這一剛度比下,盡管仍有顫振速度隨推力增大而增大的發動機穩定效應范圍,但是與γ<5時相比,顫振速度隨推力變化的突變拐點不再存在,這是由于在該剛度比下,發動機推力和氣動力中所包含的不穩定因素相互作用的機理發生了改變[4],導致不同彎扭剛度比值(γ=1,2,10)所對應的顫振包線變化趨勢明顯不同。

4 結 論

本文采用CFD與Simo幾何精確梁模型耦合的求解算法,發展了考慮發動機推力作用的機翼顫振分析方法。以帶發動機的大展弦比機翼為研究對象,分析了發動機推力、安裝位置、集中質量以及機翼彎扭剛度比等參數對機翼顫振邊界的影響,得到如下結論:

(1)本文方法將CFD和Simo梁理論引入到考慮發動機推力的機翼顫振求解中,在流場求解方面完善了當前對該問題僅采用線性氣動力模型的不足,在結構求解方面豐富了大柔性梁結構的建模方法;

(2)機翼顫振分析的仿真結果,可為提高翼吊式柔性機翼的氣動彈性穩定性提供可行的設計和布局方式;

(3)本文方法可為研究跨聲速巡航下采用翼吊式氣動布局的軍機/民機的發動機推力對機翼顫振特性的影響,以及研究起飛和著陸等特殊構型下發動機推力對機翼氣動彈性穩定性的影響,提供理論基礎。