新型功率分流混合動力系統能量管理預測優化

趙治國,王茂垚,郭元強,王建光

(1.同濟大學新能源汽車工程中心,201804,上海;2.山東聯誠精密制造股份有限公司,272100,山東濟寧)

作為深度混合動力汽車重要解決方案的功率分流混合動力系統,因其可利用行星排結構將發動機及電機的輸出功率進行分流與匯流,實現發動機端與動力輸出端轉速、轉矩的完全解耦,從而充分發揮了混合動力汽車的節油潛力,實現了較好的燃油經濟性[1]。功率分流混合動力系統方案已經在國際幾款車型上取得了巨大的成功,如豐田的THS系統、通用的VOLTEC系統等[2-3]。

能量管理策略是功率分流混合動力汽車節能的關鍵技術,一般包括邏輯門限值[4]、模糊控制[5]等基于規則的能量管理策略,等效燃油消耗最小[6]等瞬時優化策略,動態規劃[7]、最小值原理[8]等全局優化策略。規則的能量管理策略簡單易行,卻難以保證優化效果;瞬時優化策略的效果依賴于油電轉化因子的準確性,而針對功率分流混合動力系統沒有一個足夠準確的方法確定其參數;全局優化策略則需要提前預知工況信息,難以運用于實際車輛的控制中。隨著研究的深入,基于模型預測控制的局部優化能量管理策略越來越受到重視[9]。基于模型預測控制能量管理策略通過建立精確的預測模型,在每一個時刻基于系統的當前及過去狀態信息,預測未來一段時間內的電池荷電狀態(SOC)變化及發動機燃油消耗,并將其引入到成本函數中,通過局部尋優手段求解出預測時域內各動力源最優轉矩分配序列,并將第一個控制量即當前控制量作用給系統。因為在每一個時刻都會將系統的狀態量引入預測模型構成反饋校正,故基于模型預測控制的能量管理策略具有較好的魯棒性[10]。同時,相比于瞬時優化能量管理策略,基于模型預測控制能量管理策略可做到短時域內最優,相比于全局優化能量管理策略可以大大減少計算量。由于功率分流混合動力汽車是一個復雜的系統,涉及動力電池、發動機等諸多強非線性元件,故常規優化方法難以直接運用到能量管理優化問題之中。

針對插電式混合動力汽車的能量管理問題,何洪文等將模型預測控制思想用于動態規劃算法中,通過多步馬爾科夫預測方法預測混合動力客車駕駛工況,構建預測時域內能量管理優化問題,并運用動態規劃算法實現各動力源的轉矩的最優分配[11]。連靜等針對并聯式混合動力汽車在新歐洲行駛工況(NEDC)下的燃油經濟性進行全局優化分析,獲取特定工況下動力電池SOC的變化規律,將基于動態規劃離線計算的SOC軌跡作為模型預測控制的參考軌跡,開發了既定工況下模型預測控制能量管理策略[12]。

針對功率分流混合動力汽車的能量管理優化問題,Borhan等首次將模型預測控制應用于功率分流混合動力汽車的能量管理中,將模型預測控制問題轉化為預測時域內的二次規劃問題,在每一個決策時刻通過對二次規劃問題的求解得到各動力源的最優轉矩控制序列,實現了基于模型預測控制能量管理策略的初步應用[13]。袁洪亮等在考慮功率分流系統機械及電氣特性的前提下,將模型預測控制與二次規劃求解方法結合起來,實現了針對豐田Prius功率分流混合動力汽車能量管理策略的開發[14]。項昌樂等將模型預測控制的思想與動態規劃結合起來,通過馬爾科夫鏈預測有限時域內的功率分流混合動力汽車的車速變化,在有限時域內運用動態規劃算法求解能量管理的最優解,最終決策出發動機及電機的控制量[15]。Zhu等采用極小值原理對預測時域內的能量管理問題進行計算,實現了對預測駕駛員需求轉矩的跟蹤[16]。王偉達等通過構建狀態觀測器實時觀測電池SOC的狀態,將模型預測能量管理優化問題轉化為線性二次型最優控制問題[17]。此外,還有人采用迭代算法[18]、一維搜索算法[19]等對預測時域內的能量管理優化問題進行計算,以實現模型預測控制在能量管理中的應用。

針對新型雙模功率分流混合動力系統方案,本文提出基于系統當前及歷史狀態信息的發動機工作點最優決策律,深入分析不同功率分流模式下轉速轉矩關系,研究發動機、電機及動力電池的工作機理及特性,并建立了功率分流混合動力系統短時域預測模型,提出了基于發動機最優決策律的能量管理優化策略。

1 新型雙模功率分流混合動力系統

1.1 構型方案

如圖1所示,該新型雙模功率分流混合動力系統由共用行星架的雙行星排構成,發動機通過單向離合器連接前行星排太陽輪,電機1連接前行星排齒圈,并通過離合器與后行星排齒圈連接,后行星排齒圈又通過制動器鎖止。電機2連接后行星排太陽輪,行星架連接在一起作為整個行星排系統的輸出。通過離合器和制動器不同的作動狀態,可實現5種工作模式,其中有兩種功率分流工作模式,如表1所示。整車參數與設計指標見表2,動力系統關鍵部件參數見表3。

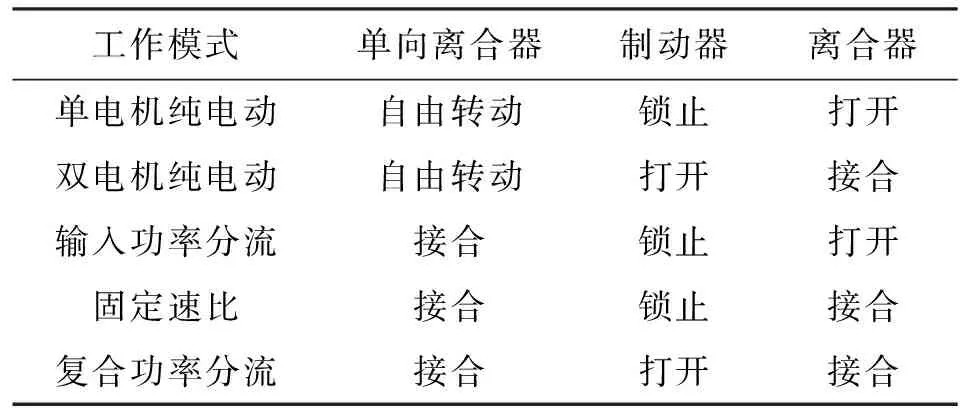
表1 工作模式一覽表

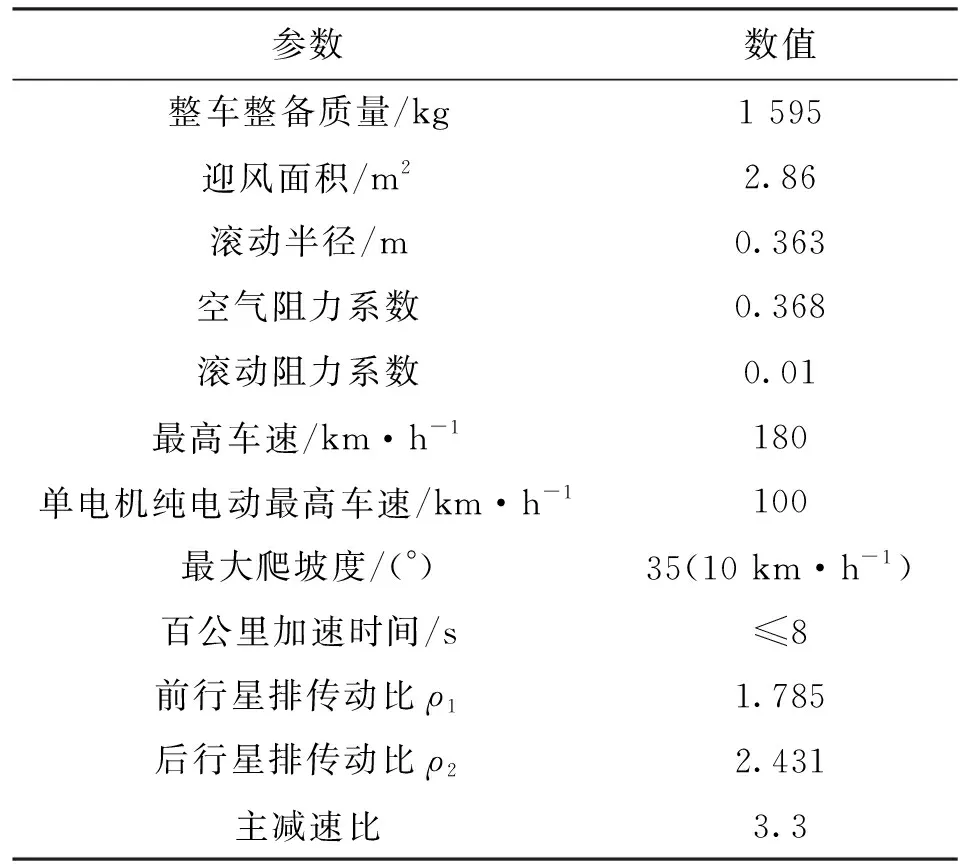
表2 整車參數與設計指標

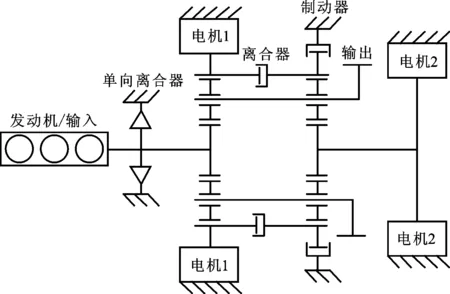
圖1 新型功率分流混合動力系統結構

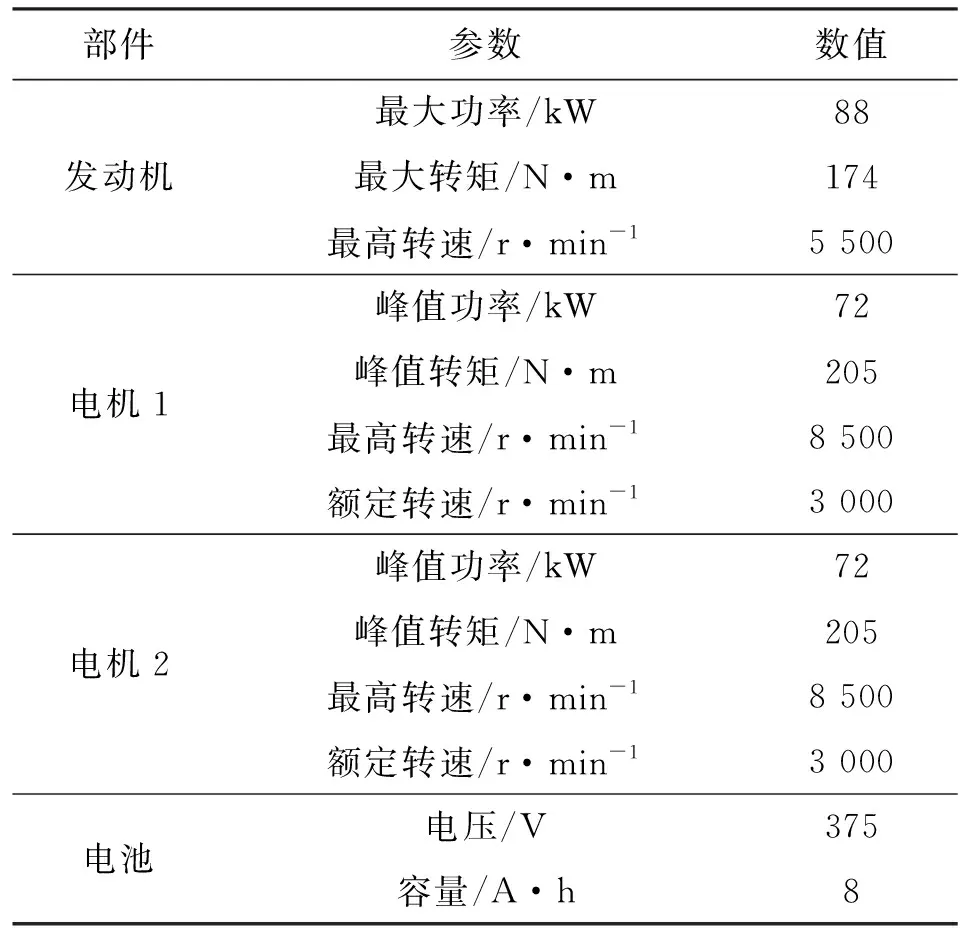
部件參數數值發動機最大功率/kW88最大轉矩/N·m174最高轉速/r·min-15 500電機1峰值功率/kW72峰值轉矩/N·m205最高轉速/r·min-18 500額定轉速/r·min-13 000電機2峰值功率/kW72峰值轉矩/N·m205最高轉速/r·min-18 500額定轉速/r·min-13 000電池電壓/V375容量/A·h8

1.2 數學模型

針對上述新構型方案,忽略各軸及其齒輪的旋轉黏性阻尼的作用、嚙合齒輪的嚙合彈性、軸承及軸承座間的彈性作用,將車輪轉動慣量以及車輛平動質量統一折算到變速箱輸出軸,由此可得混合動力變速箱各部件轉矩關系式

TENG-TS1=JENGαENG

(1)

TM1-TR1=JM1αM1

(2)

TM2-TS2=JM2αM2

(3)

式中:J、α分別為等效轉動慣量、角加速度;T為轉矩;下標ENG表示發動機(包括曲軸、飛輪、單向離合器等),M1、M2分別表示電機1、電機2,S1、S2和R1分別表示前、后行星排太陽輪及前行星排齒圈。

考慮行星排系統的轉動慣量相對于發動機及電機的轉動慣量比較小,進而忽略太陽輪、行星架及齒圈等的轉動慣量,由此可得如下行星排的轉矩轉速平衡方程。

對于輸入功率分流模式,有

TS1+ρ2TS2+TR1=TOUT

(4)

ρ1ρ2TS2+(1+ρ1)TR1=ρ1TOUT

(5)

ρ1nM1+nENG=(1+ρ1)nOUT

(6)

nM2=(1+ρ2)nOUT

(7)

對于復合功率分流模式,有

TS1+TS2+TR1=TOUT

(8)

(1+ρ1)TS1+(1+ρ2)TS2=TOUT

(9)

ρ1nM1+nENG=(1+ρ1)nOUT

(10)

ρ2nM1+nM2=(1+ρ2)nOUT

(11)

式中:T為折算的等效阻力矩;n為轉速;下標OUT表示輸出端(即行星架)。

考慮行星排系統在穩態運行工況下其齒間隙及傳動軸阻尼等均可忽略,

由式(6)(7)可得輸入功率

分流模式下各動力源的加速度關系表達式,由式(10)(11)可得復合功率分流模式下各動力源的加速度關系表達式

ρ1αM1+αENG=(1+ρ1)αOUT

(12)

αM2=(1+ρ2)αOUT

(13)

ρ1αM1+αENG=(1+ρ1)αOUT

(14)

ρ2αM1+αM2=(1+ρ2)αOUT

(15)

進一步可得該新型功率分流混合動力系統統一運動學模型的矩陣表達形式[20]

AX=B

(16)

X=[TS1TS2TR1TENGTM2αM1αM2TM1

TOUTαENGαOUT]T

(17)

B=[0000000

TENGTOUTαENGαOUT]T

(18)

在輸入功率分流模式下

(19)

在復合功率分流模式下

(20)

1.3 效率分析

定義功率分流混合動力系統傳動比為發動機轉速與輸出端轉速的比值,當電路凈輸出功率為0時,發動機全部輸出功率都經由機械路徑傳遞到車輪,系統傳動效率最高,此時系統的傳動比稱為機械點。定義電功率循環比為功率分流模式下兩電機總功率與發動機功率的比值[21],得到機械點處電功率循環比為0。將電機及輸出端轉矩轉速相對于發動機轉矩轉速做歸一化處理,可得該雙模功率分流系統在輸入功率分流模式下的機械點為1+ρ1,而在復合功率分流模式下的機械點有兩個,分別為1-ρ1/ρ2和1+ρ1。假設兩個電機的工作效率為η1和η2,經過Matlab編程可計算輸入功率分流模式和復合功率分流模式下電功率循環比隨傳動比的變化關系如圖2所示。由圖可見:在輸入功率分流模式下,電功率循環比隨傳動比的增大先減小到0再逐漸增大;在復合功率分流模式下,電功率循環比隨傳動比的增大呈先減小后增大、而后再減小增大的復雜變化過程。

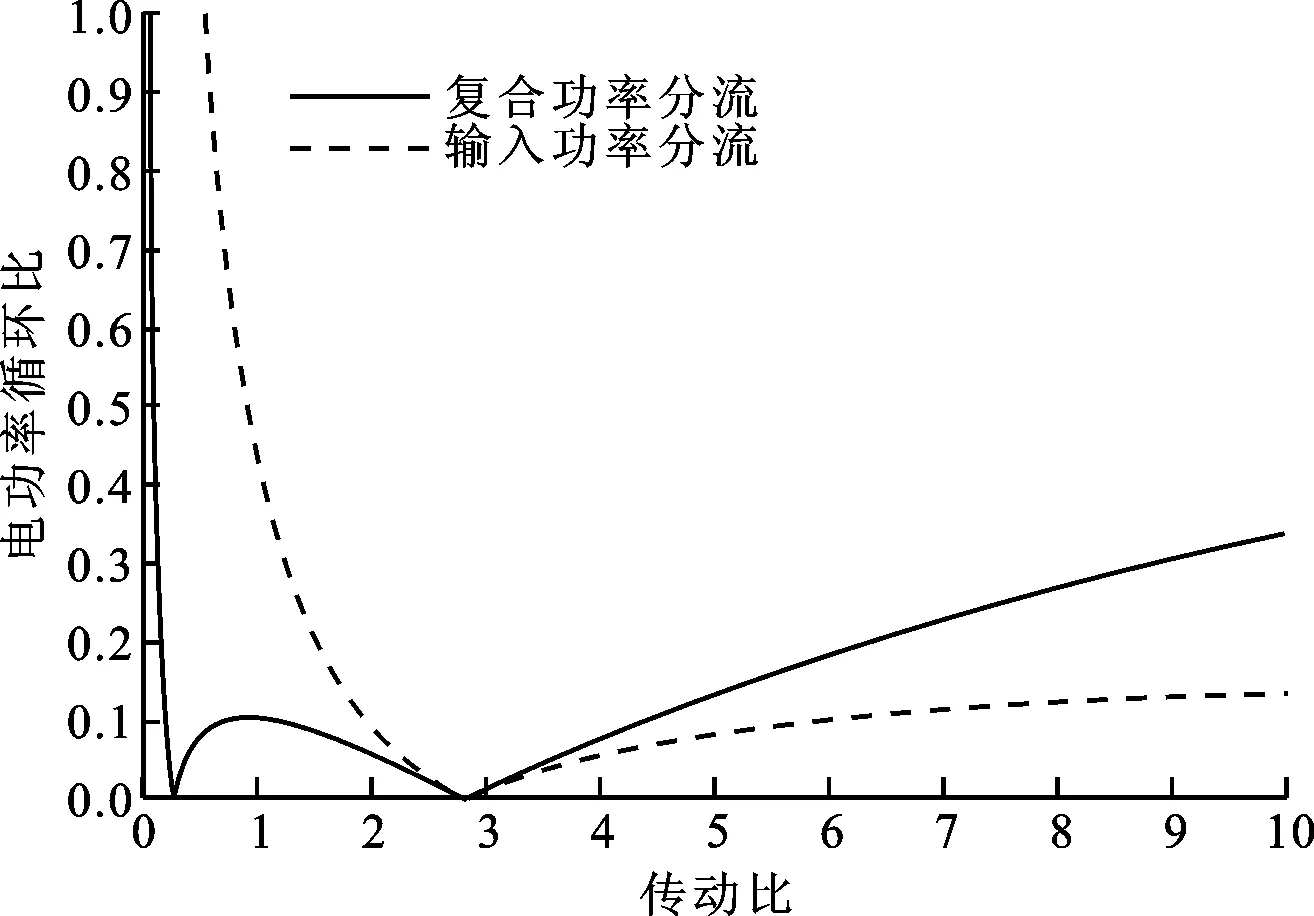
圖2 電功率循環比隨傳動比的變化關系

由于構型的特殊性,輸入功率分流的機械點同為復合功率分流的機械點之一。當傳動比大于輸入功率分流的機械點時,輸入功率分流的電功率循環比低于復合功率分流的電功率循環比,而當傳動比小于輸入功率分流的機械點時,復合功率分流的電功率循環比低于輸入功率分流的電功率循環比。在機械點處,因電功率循環比為0,故系統效率最高。當傳動比高于機械點時,因電功率循環,系統的效率會緩慢下降。當發動機轉速一定時,車速越高,傳動比越小,因此該構型的輸入功率分流模式適合用于車輛傳動比較大的低速行駛中,而復合功率分流模式更適合用于傳動比較小的高速行駛中。

2 功率分流混合動力系統模型

2.1 發動機模型

該新型雙模功率分流混合動力系統使用阿特金森循環發動機,其萬有特性如圖3所示。在發動機模型中,發動機的工況點及其燃油消耗率mf可由轉速和轉矩決定,即

mf=Map(nENG,TENG)

(21)

為方便構建預測模型,采用分段擬合函數法對發動機穩態燃油消耗Map圖進行擬合,即

mf=mTENG+n/TENG+l,nENG∈ψ

(22)

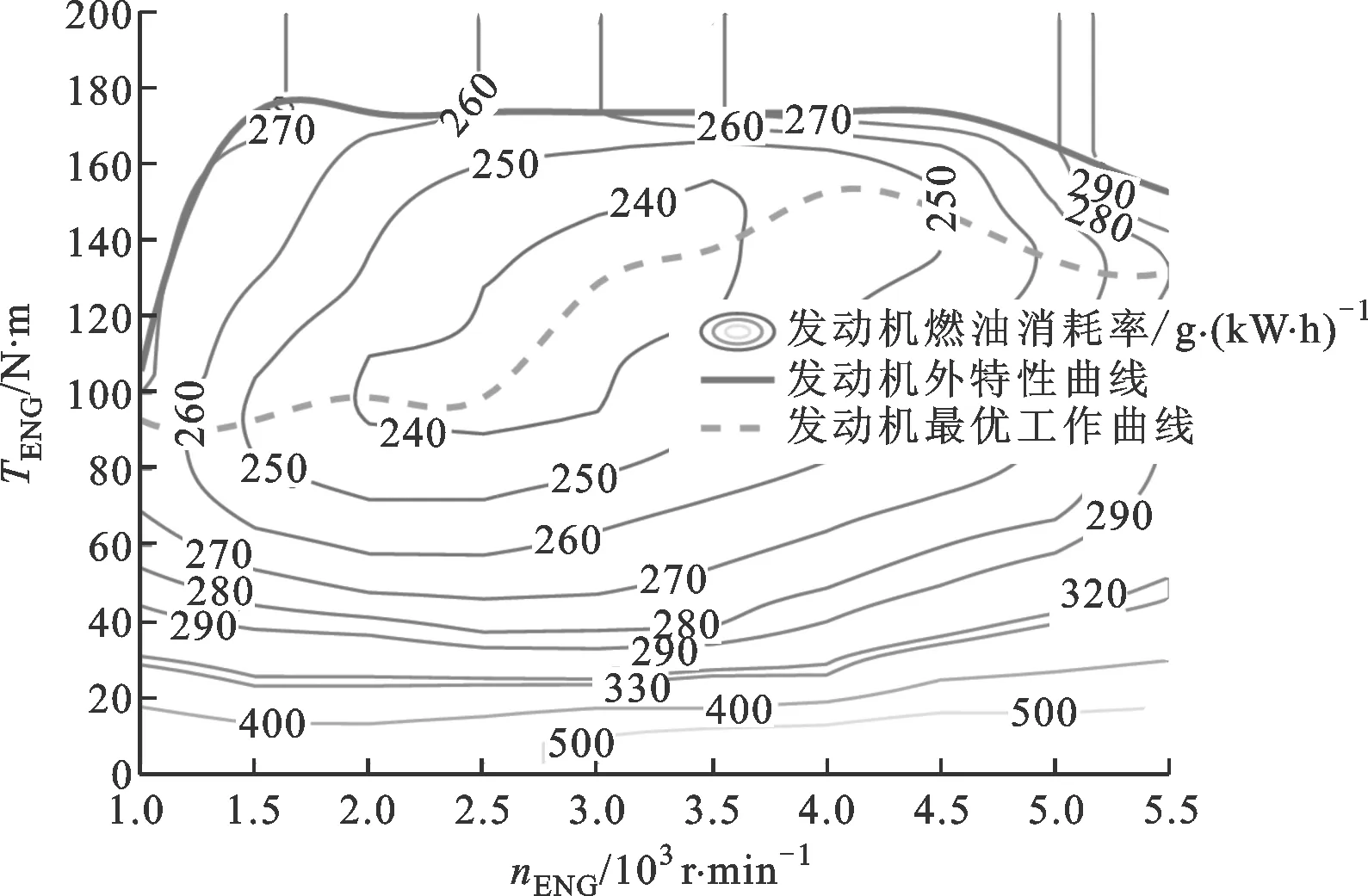
圖3 發動機萬有特性圖

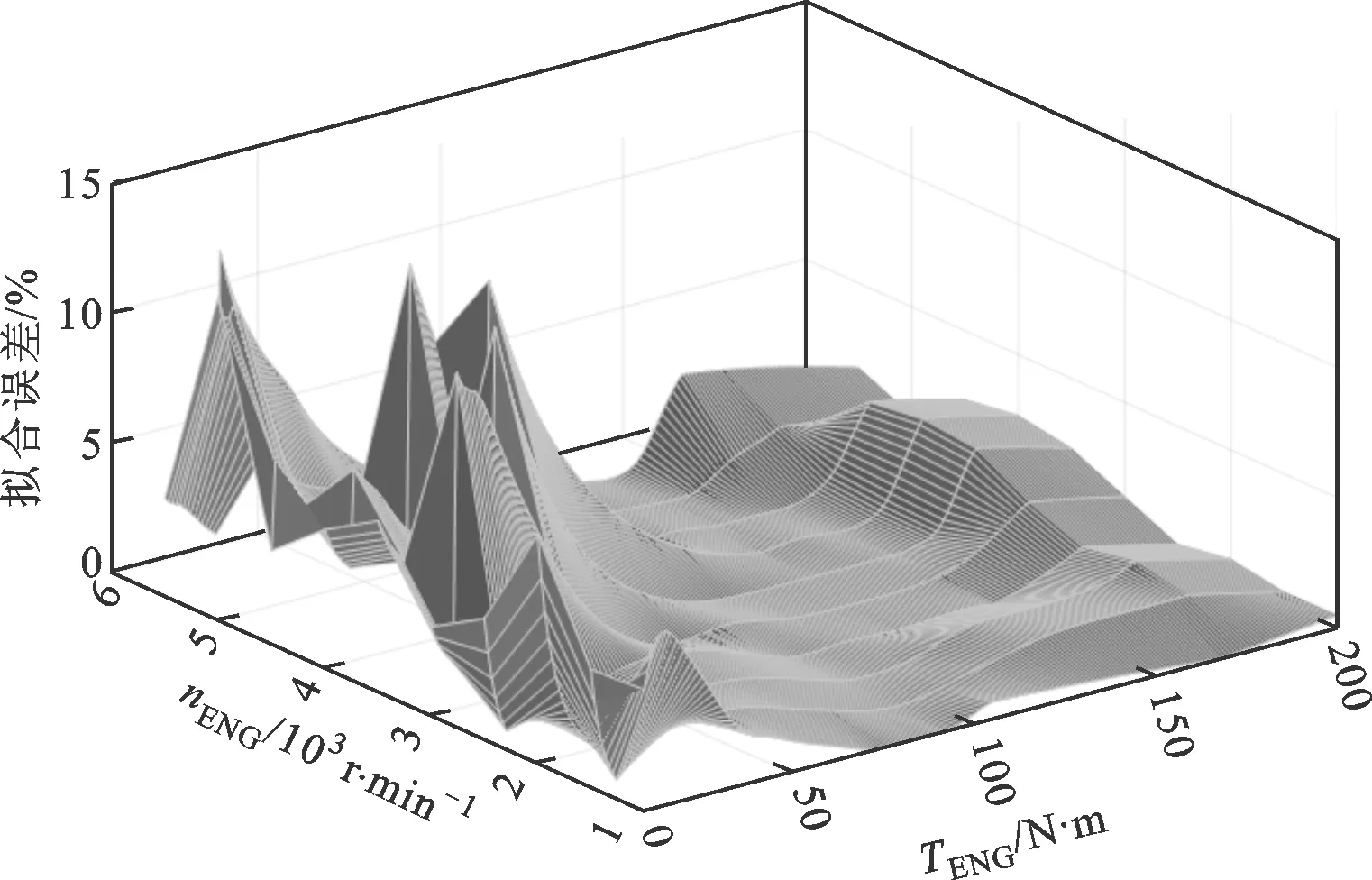
圖4 發動機燃油消耗率擬合誤差

擬合誤差如圖4所示。從圖中可以看出,當發動機轉矩低于40 N·m時,燃油消耗率擬合誤差較大,而當發動機轉矩高于40 N·m時,燃油消耗率擬合較好,誤差可保證在8%以內。考慮到發動機正常工作時輸出轉矩一般較大,故認為發動機燃油消耗率擬合較好。

2.2 電機模型

相比于發動機等機械部件,電機轉矩響應速度較快,此構型方案所用的兩電機為同一型號。這里忽略電機的磁、熱效應,僅考慮電機在不同工況下的損耗,即電機的效率與電機轉速和轉矩的函數關系。通過實驗,得到隨轉速和轉矩變化的電機效率特性曲線如圖5所示。

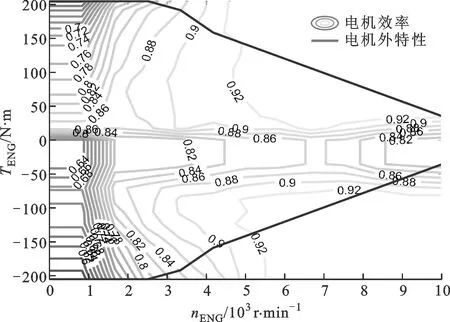
圖5 電機效率特性曲線

2.3 動力電池模型

忽略溫度的影響,動力電池簡化為一階模型,如圖6所示。

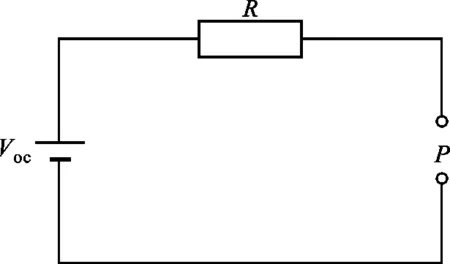
圖6 動力電池一階等效模型

動力電池電回路方程如下

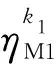
(23)

(24)

式中:P為電回路負載功率;η為電機的效率;k1、k2為電機1、電機2的充放電狀態,發電狀態為1,電動狀態為-1;R為電池內阻;Voc為電池開路電壓;I為電回路電流。

電池荷電狀態ψSOC的表達式為

(25)

聯立式(23)～式(25)并求導,可得

(26)

(27)

3 基于模型預測控制的能量管理策略

模型預測控制的機理可描述為:在每一個采樣時刻根據當前系統已知的測量信息,通過預測模型預測未來有限時域內的輸出,在線優化未來時刻輸出可得到相應的輸入控制序列,將得到的控制序列的第一個元素作用于被控對象;在下一個循環時刻重復上述過程,用新的測量值刷新優化問題并重新求解[22]。模型預測控制是一種實時優化算法,為了滿足實時性,其預測模型不能復雜,故采用擬合函數法對發動機萬有特性進行建模,采用安時積分法對動力電池進行建模。功率分流混合動力系統包含了發動機、電機及動力電池組等多個部件,均具有較復雜的非線性特性。對于非線性系統而言,當非線性因素對系統影響很小時一般可將其忽略,如果系統的變量在工作點附近只發生微小的偏移,可以通過取其線性主部用切線法進行線性化,故當設置預測時域較短時,在預測時域內輸出端的需求轉矩也近似認為不變。

3.1 預測模型

取系統的狀態變量與輸出變量為ψSOC、mf,控制變量為nENG、TENG,干擾變量為TOUT、nOUT,即

(28)

y=C·x

(29)

(30)

(31)

x=F(u,v)

(32)

式(32)是電池SOC及發動機燃油消耗率的隱函數表現形式,對上述系統非線性模型在每一個采樣時刻做最優線性逼近,可得泰勒展開表達式

(33)

基于較短預測時域尺度假設,可認為在預測時域內輸出端的需求轉矩及轉速近似不變,由式(32)可得預測時域內線性化模型

x=F0+gΔu

(34)

y=C·x

(35)

(36)

(37)

實際應用中為了滿足在線數值計算的需求,需要將以上獲得的連續系統模型在預測時域內轉化為離散化模型

Y=GΔU+F

(38)

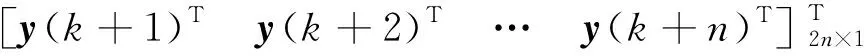
(39)

(40)

ΔU=

(41)

(42)

F=

(43)

(44)

式中:y表示輸出;Δu表示控制量變化;F0為由式(37)算出的泰勒展開偏差量;(k+i)表示k+i時刻;gi為由式(36)算出的線性主部系數,是一個2×2的矩陣。

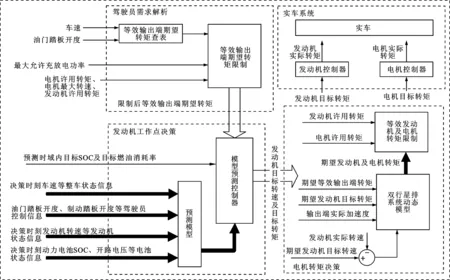
圖7 模型預測控制能量管理策略架構

3.2 最優決策律

功率分流混合動力汽車能量管理策略的主要目的是使得系統在滿足約束的條件下,獲得最佳的燃油經濟性,并且保持動力電池SOC在其參考值附近變化。預測時域內目標SOC及目標燃油消耗率

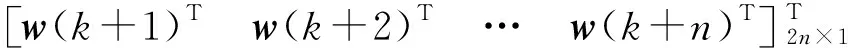
(45)

(46)

式中:w(k+i)表示k+i時刻目標SOC及目標燃油消耗率所組成的向量;ψSOCtrg(k+i)表示k+i時刻目標SOC;mftrg(k+i)表示k+i時刻目標燃油消耗率。

在滾動時域內滿足諸多約束的前提下,既要使得動力電池SOC維持在參考值附近,又要使得發動機的燃油消耗盡可能小,為此在代價函數中添加控制量增量懲罰項,以確保在控制時域內控制量增量的合理變化,即

J=(Y-W)TQ(Y-W)+λΔUTΔU

s.t.Y?Ψ;ΔU?Ω

(47)

式中:Q為預測時域內各項輸出的罰函數對角陣;Ψ為預測輸出的有效集;Ω為控制變化量的有效集。

系統狀態變量約束條件為

ψSOCmin≤ψSOC(t)≤ψSOCmax

(48)

控制變量約束為

Tmin≤TENG(t)≤Tmax

nmin≤nENG(t)≤nmax

ΔTmin≤ΔTENG(t)≤ΔTmax

Δnmin≤ΔnENG(t)≤Δnmax

(49)

基于最優控制理論,令

(50)

可得控制時域內最優控制律為

ΔU=(GTQG+λI)-1GTQ(W-F)

(51)

實際控制時每次僅將第一個分量加入系統,即

u(k)=u(k-1)+gT(W-F)

(52)

式中:gT為(GTQG+λI)-1GTQ的第一行。根據系統當前及歷史狀態信息,在每一個決策時刻更新式(52)中各系數矩陣,即可快速決策發動機工作點。

3.3 能量管理策略架構

基于模型預測控制(MPC)的能量管理策略架構如圖7所示,其中模型預測控制器用于決策發動機轉矩及轉速;轉矩分配控制器在考慮整車約束及功能安全的前提下,根據需求轉矩及已決策出的發動機轉矩和轉速來決策相應兩電機轉矩,最終決策出每一個時刻發動機及兩電機的目標轉矩[23]。

4 仿真測試及結果分析

4.1 仿真結果分析

為了驗證基于模型預測控制的能量管理策略的有效性,在Matlab/Simulink中搭建功率分流混合動力系統模型及相應的控制策略,以NEDC工況為例進行仿真測試。設置初始ψSOC為60%,預測時域和控制時域均為3 s,設置仿真步長為0.01 s,一個仿真步長內發動機最大轉矩增量不超過2 N·m,發動機最大轉速增量不超過10 r·min-1。

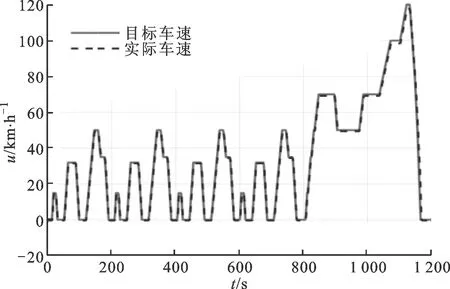
圖8 MPC能量管理策略下車速跟蹤圖

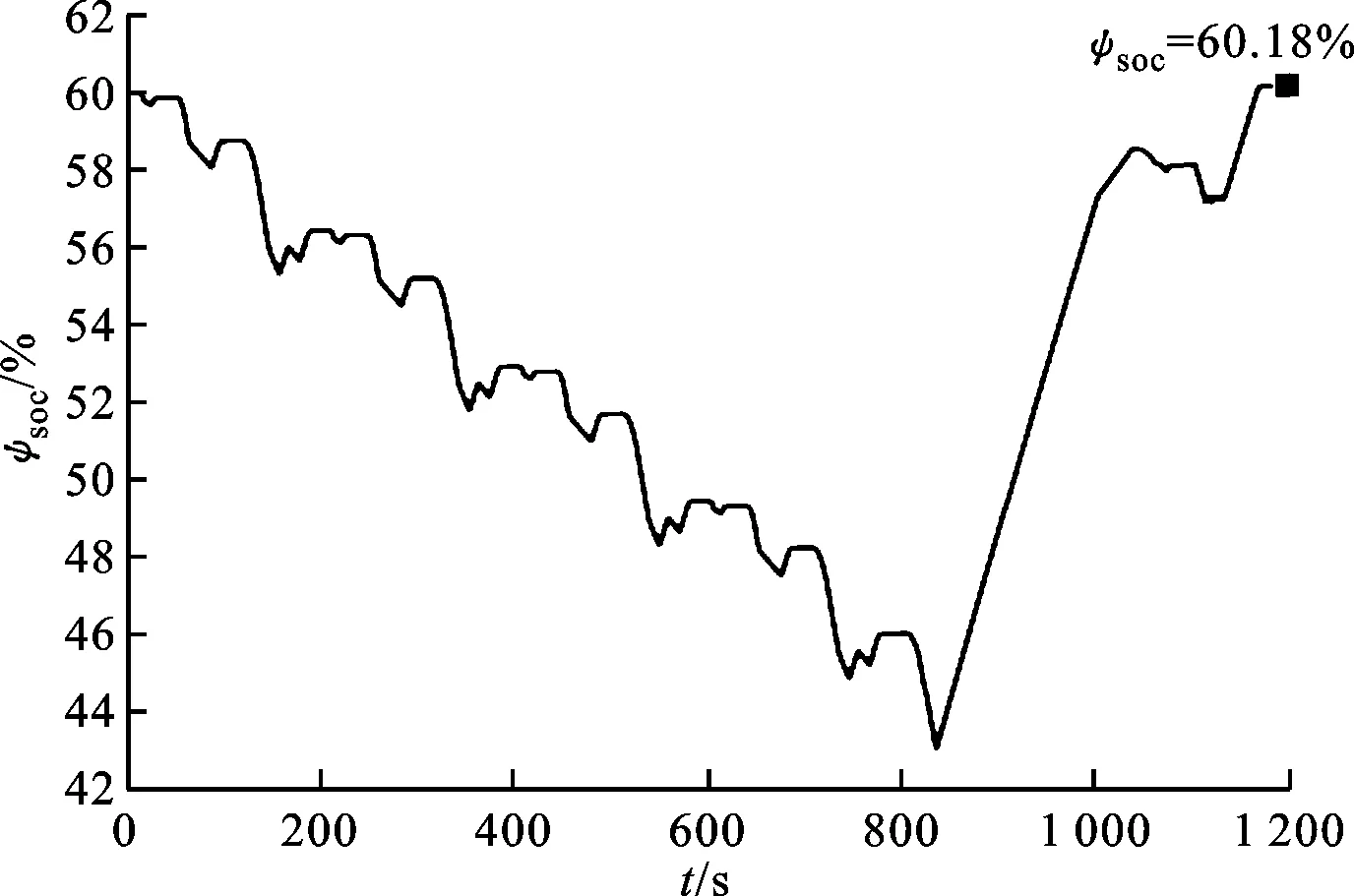
圖9 MPC能量管理策略下SOC變化圖

圖8為NEDC工況車速跟蹤圖,可以看出,基于模型預測控制的能量管理策略能很好地實現整車控制功能,完成車速跟蹤。圖9為NEDC仿真工況下SOC的變化圖,初始時刻的ψSOC設置為60%,終了時刻的ψSOC為60.18%,絕對誤差為0.18%,說明該控制策略能夠實現SOC的基本穩定。在800 s前,由于以純電動模式為主,SOC振蕩下降;在800 s后,輸入功率分流模式和復合功率分流模式成為驅動整車運行的主要模式,SOC快速上升,并維持在SOC目標值60%左右。圖10為整個NEDC工況下發動機工作點的分布圖。從圖中可以看出,基于模型預測控制的能量管理策略能夠使發動機工作在最優工作區間。圖11為NEDC工況下發動機及兩電機轉矩的變化過程圖,圖12為NEDC工況下整車模式變化過程圖,圖13為NEDC工況下發動機及兩電機轉速的變化過程圖。經過多個NEDC仿真工況后,得到百公里油耗平均為4.95 L。

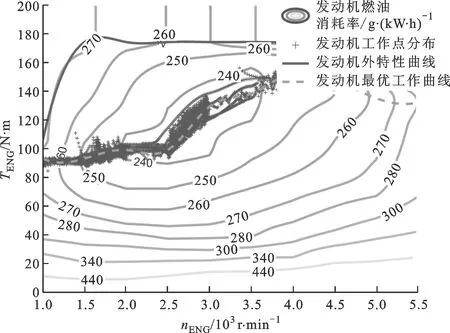
圖10 MPC能量管理策略下發動機工作點分布圖

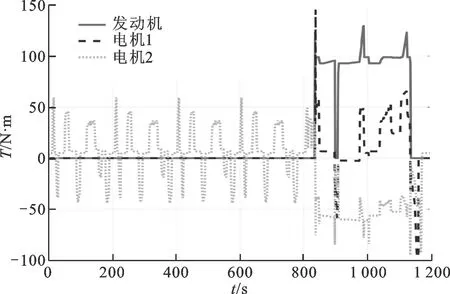
圖11 MPC能量管理策略下發動機及電機轉矩圖

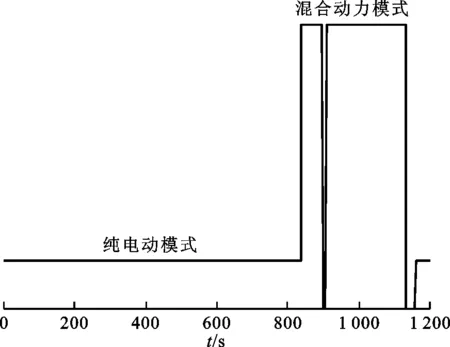
圖12 MPC能量管理策略下工作模式變化圖

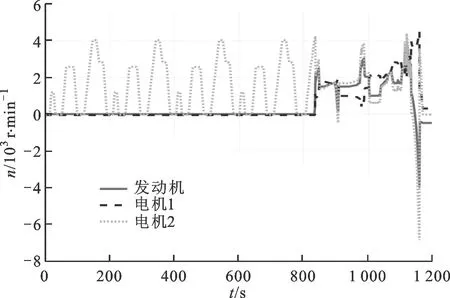
圖13 MPC能量管理策略下發動機及電機轉速圖

4.2 基于規則的能量管理策略

如圖14所示,基于規則能量管理策略根據車速、SOC及踏板開度信息決策駕駛員需求轉矩及當前最佳工作模式。在純電動模式下,將由電機直接提供駕駛員需求轉矩;在混合動力模式下,先根據駕駛員需求功率查最佳發動機需求轉速,再根據當前發動機轉速查最佳發動機轉矩輸出范圍,在保證系統平衡且正常工作的前提下決策兩電機轉矩。

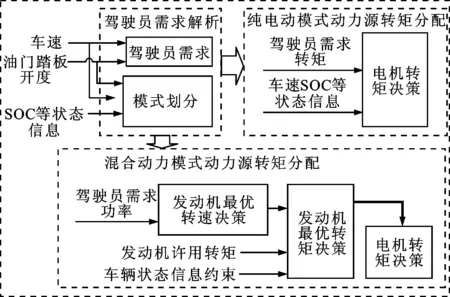
圖14 規則能量管理策略控制架構

圖15為采用規則能量管理策略NEDC工況下SOC的變化,初始時刻ψSOC也設置為60%,而終了時刻的ψSOC為67.53%。對比圖9中SOC變化過程,在0～800 s內,規則能量管理策略的SOC變化與模型預測控制能量管理策略的結果基本相同,均為振蕩下降,這是因為800 s之前兩種控制策略下整車均處于純電動工作模式。在800 s之后,由于SOC較低整車進入功率分流混合動力模式,兩種控制策略下電池的SOC均開始上升,規則能量管理策略下SOC上升幅度明顯高于模型預測控制能量管理策略下SOC的變化,導致終了時刻SOC有了明顯的上升。這是因為規則能量管理策略優先保證發動機工作在較優的區間,而忽略了混合動力汽車電氣特性的影響,故電池SOC的變化較大。圖16為采用規則能量管理策略NEDC工況下發動機工作點的分布圖,可以看出相比于圖10,規則的能量管理策略下發動機的工作點緊緊分布在最優工作線兩側。圖17為仿真過程中兩種控制策略下電機功率損失變化曲線,在800 s之前,兩種控制策略下的整車均處于純電動模式,因此電機功率損失變化曲線基本相同;在800 s之后,由于SOC較低,整車進入功率分流模式,規則控制策略下的電機損失功率略高于MPC能量管理策略。采用規則能量管理策略經過多個NEDC工況后其百公里油耗為5.364 L。相比于基于規則的能量管理策略,模型預測控制的能量管理策略可提升百公里燃油消耗約7.7%。

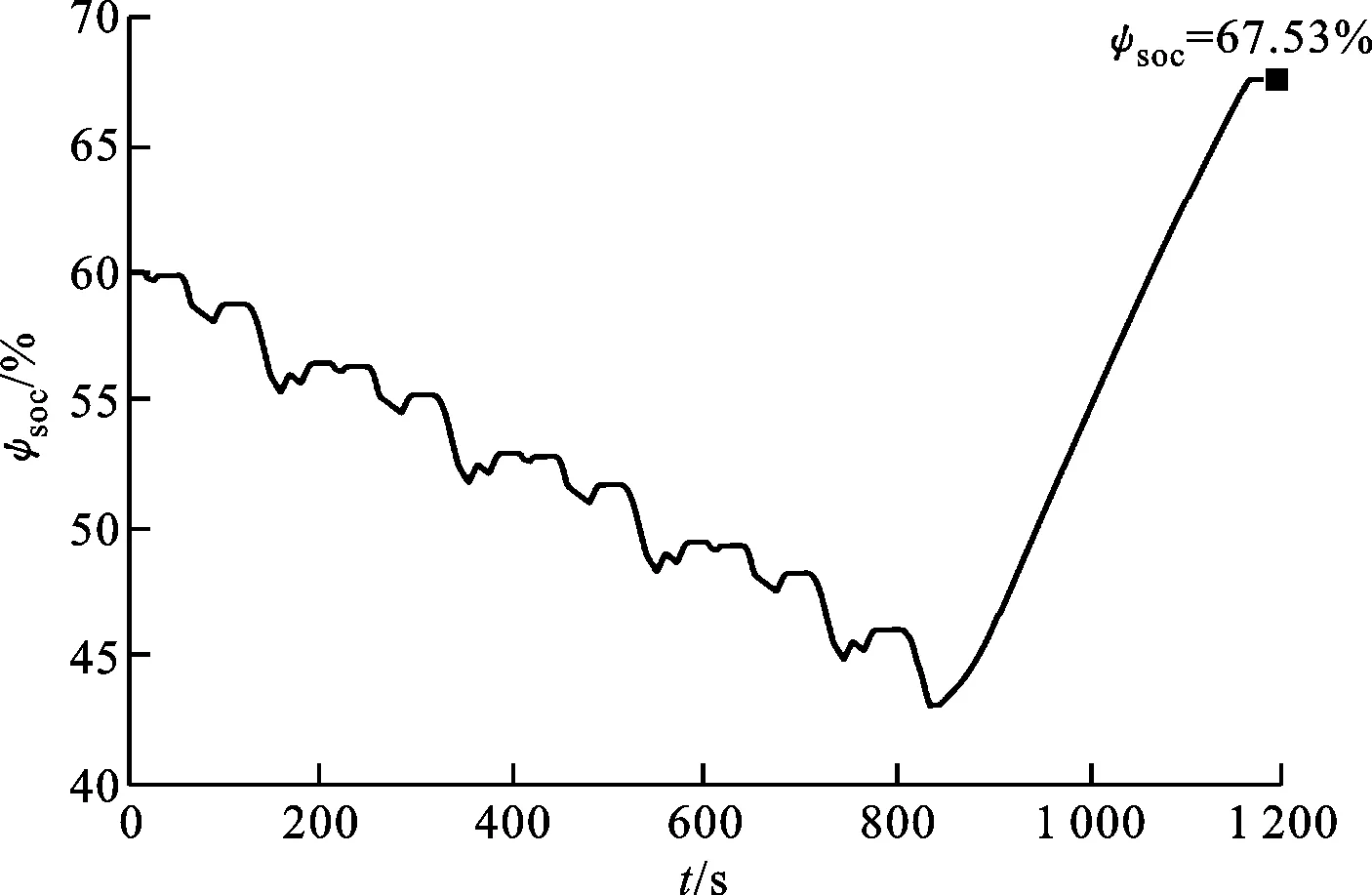
圖15 規則能量管理策略下SOC變化圖

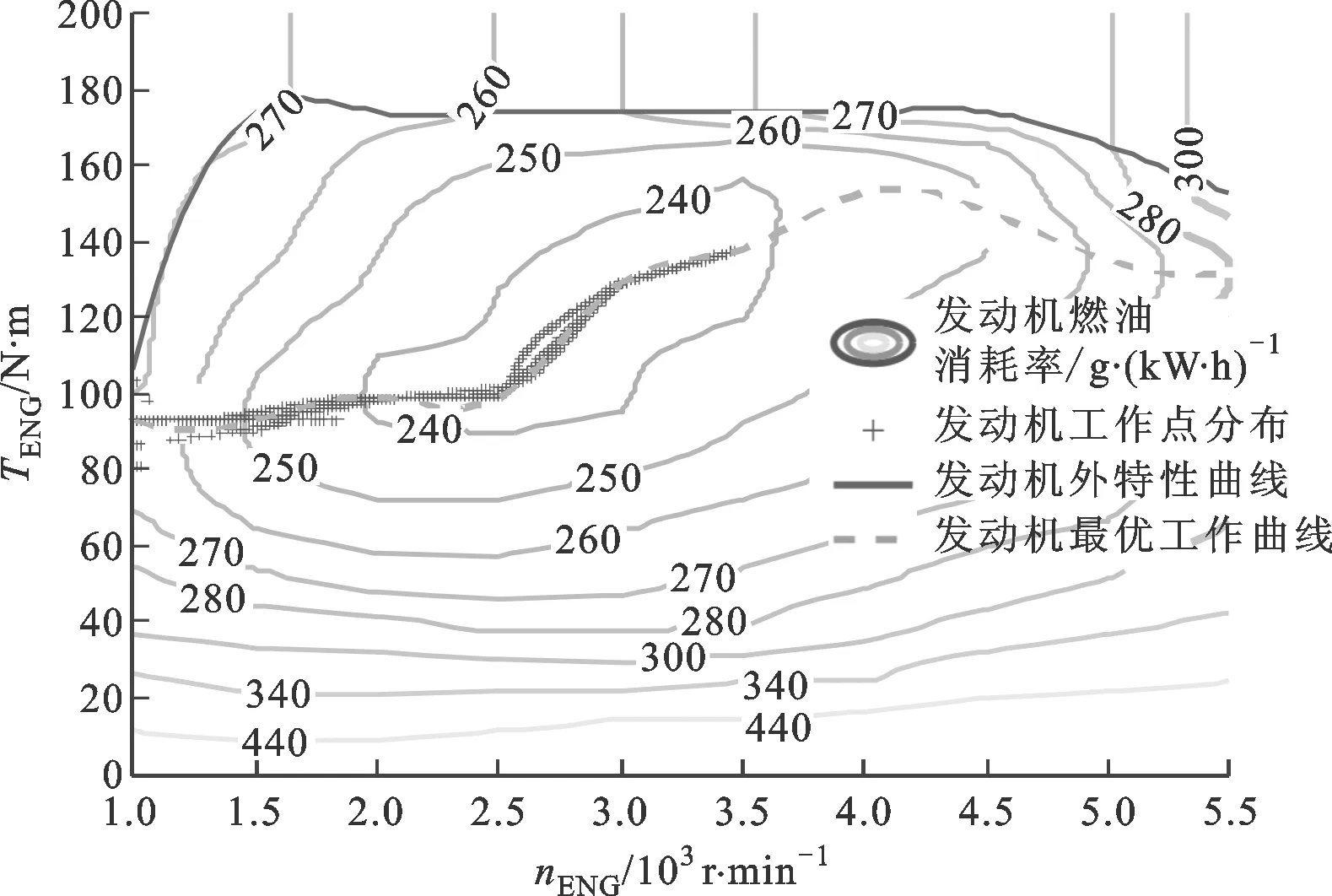
圖16 規則能量管理策略下發動機工作點分布圖

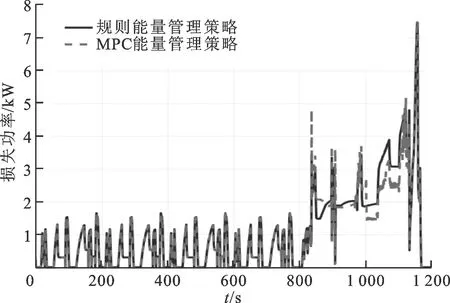
圖17 不同控制策略下電機功率損失變化曲線

5 結 論

本文以某新型功率分流混合動力系統方案為研究對象,以實時優化發動機轉矩為研究目的,重點研究混合動力模式下各動力源轉矩的實時優化控制。首先,對功率分流混合動力系統的結構及模式進行分析,采用機理研究及實驗擬合相結合的方法建立短時域預測模型;其次,以預測時域內改善發動機工作點及維持SOC的基本穩定為目標,提出了基于系統當前及歷史信息的發動機工作點最優決策方法,開發了基于發動機轉矩最優決策的能量管理策略。

NEDC仿真結果表明,基于發動機工作點最優決策的功率分流混合動力汽車MPC能量管理策略可實現各動力源轉矩的優化分配,改善整車的燃油經濟性,可保證發動機基本工作在最優的工作區間的同時,又能兼顧混合動力汽車電氣特性對燃油經濟性的影響,對于工程實踐具有一定的參考價值。