低溫管路預冷過程兩相流動與換熱計算研究

王嬌嬌,陳虹,厲彥忠,,王磊,李翠

(1.西安交通大學能源與動力工程學院,710049,西安;2.航天低溫推進劑技術國家重點實驗室,100028,北京)

近年來低溫流體的應用日益廣泛,液化天然氣(LNG)、液氧(LOX)、液氮(LN2)、液氫(LH2)和液氦(LHe)等經常作為燃料或冷卻劑廣泛應用于各行業。液氫、液氧具有高比沖、大推力、無毒無污染等優點,被認為是未來深空探測的首選推進劑,然而由于其飽和溫度低、氣化潛熱小,與外部環境溫差較大,在運輸及使用過程中極易發生劇烈氣化。因此,在低溫流體傳輸、加注之前需進行小流量預冷加注,將管路從室溫降至低溫區。在此過程中,降低預冷時間和減少低溫推進劑消耗量具有重要的意義。因此,為了實現預冷過程的準確控制并最大限度地減少低溫液體消耗,需對預冷過程的瞬態熱傳遞機制開展深入研究。

由于管壁與流體溫差較大、壓力和速度波動劇烈以及復雜的兩相流動與換熱,使得相關研究面臨較大挑戰,低溫流體預冷管路沸騰換熱主要依靠實驗研究。近年來,研究人員針對液氮預冷沸騰開展了大量實驗研究,為減少復雜性,研究者通常把預冷沸騰的各種影響因素孤立起來進行實驗,進而分析各因素對過程發展的影響和作用機制[1]。Velat等指出質量流速是預冷過程重要的影響因素[2-3],Hu等分別進行不同方向預冷實驗,發現豎直向上管路預冷速度快于豎直向下[4]。Shaeffer等研究了流動方式的影響,得到間歇流動方式利于減少推進劑消耗量[5]。Hartwig等研究了工質對流動沸騰的影響[6]。在此基礎上,Darr等對液氮管路流動沸騰開展大量的實驗研究,為理論分析和機理研究提供了大量數據[7-10]。目前,預冷沸騰方面的相關理論研究較少,主要沿用傳統兩相流動與換熱理論。Chung等建立的兩流體模型在一定條件下與實驗結果比較符合[11-13]。孫恒等采用均相模型[14-15],余紅梅等采用氣液同速推進分層流動模型[16],對低溫流體預冷管路過程進行預測,均取得一定進展。

綜上所述,由于低溫管路預冷沸騰機理的復雜性、隨機性、多樣性以及非穩態的發展過程,相關研究還很不充分,不確定因素和未知現象較多。因此,本文構建了有效的低溫管路預冷模型,利用多個文獻中的實驗數據驗證了模型的有效性,并對預冷過程中的流型與換熱特性及非穩態降溫特性開展了預測與分析。

1 控制方程

1.1 低溫液體流動與換熱方程

本文采用一維均相模型描述預冷過程中管內低溫流體,將氣液兩相處理為混合均勻的、具有平流動特性和平均物性的單一流體,假設管流為一維流動,采取準穩態描述方式,兩相之間處于熱、力平衡。管路中流體流動與換熱的控制方程為

連續性方程

式中:ρ為流體密度;A為管路截面積;u為流體速度;t為時間;x為管路軸向坐標。

動量方程

式中:P為壓力;fR為摩擦因數;θ為重力場與管流方向夾角;g為重力加速度。

能量方程

式中:γ為焓值;Sh為單元體管路壁面與低溫流體間的換熱量。

1.2 管壁一維非穩態導熱方程

在預冷過程中,管壁溫度從室溫降至低溫區,一維非穩態導熱方程(忽略軸向導熱)為

式中:ρs為管路壁面固體密度;cp,s為管路壁面熱容;λs為管路壁面導熱系數;Tw為壁面溫度;r為管路徑向坐標。

管路內壁面與管內流體對流換熱,管路外壁面與外界環境換熱,內外壁面邊界方程分別為

式中:hconv為內壁面與流體之間換熱系數;qpar為外界環境漏熱熱流。

1.3 真空絕熱管路的漏熱計算

真空絕熱管路的外界環境漏熱包括輻射換熱和殘余氣體導熱兩部分,其中輻射換熱可根據斯蒂芬-玻爾茲曼方程計算,即

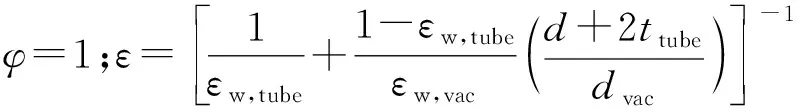
殘余氣體導熱根據下式進行計算

qgc=kβPvam(Tw,vac-Tw)

1.4 管壁與流體間的換熱計算

圖1展示了不同文獻中液氮預冷沸騰曲線的實驗數據,由圖1可知,不同工況的實驗結果具有相同趨勢,隨著壁面過熱度的降低,膜態沸騰起始溫度TMFB、臨界熱流CHF、核態沸騰起始溫度TONB這3個特征點將流體與管壁間換熱依次分為膜態沸騰、過渡沸騰、核態沸騰、單相強制對流4種方式。

由于低溫流體物性的特殊性和預冷過程的復雜性,相關研究面臨較大挑戰。Hartwig等將多個低溫預冷實驗數據與傳統經驗關聯式進行比較[17],

發

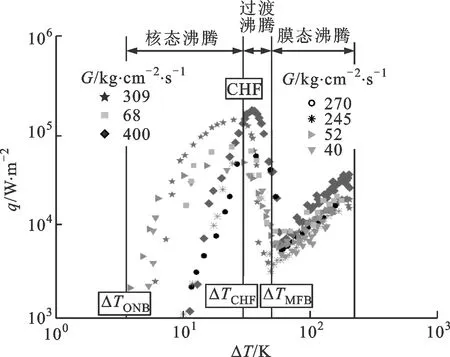
圖1 液氮管路預冷過程沸騰曲線

現所有模型與實驗數據的誤差都非常大,不能預測低溫流體預冷管路過程的換熱特性。

基于文獻中液氮預冷管路的實驗數據,本文對3個特征點和4種換熱方式的模型分別進行選擇,選擇結果及與實驗數據的對比情況如表1所示。

預冷過程中管內流體依次經歷單相氣體強制對流、膜態沸騰、過渡沸騰、核態沸騰和單項液體強制對流,不同換熱方式分別采用不同公式計算換熱系數,如圖2所示。若質量含氣率大于1或小于0,則流體與壁面間為單相強制對流換熱,采用Dittus-Boelter公式或修正的公式。若質量含氣率處于0與1之間,則流體與壁面處于兩相換熱方式。此時根據流量、壓力等參數計算膜態沸騰起始點溫度TMFB和核態沸騰起始點溫度TONB,若壁面溫度Tw大于TMFB,則處于膜態沸騰區域,采用Darr膜態沸騰換熱公式;若壁面溫度Tw小于TONB,則使用Dittus-Boelter公式進行計算;若壁面溫度Tw處于TONB與TMFB之間,則流體與壁面之間換熱為核態沸騰或過渡沸騰,通過Chen公式計算qNB,修正的Katto公式計算qCHF,若qNB小于qCHF,則處于核態沸騰,采用Chen公式;若qNB大于qCHF,則處于過渡沸騰,采用插值計算。

表1 管壁與低溫流體間傳熱模型

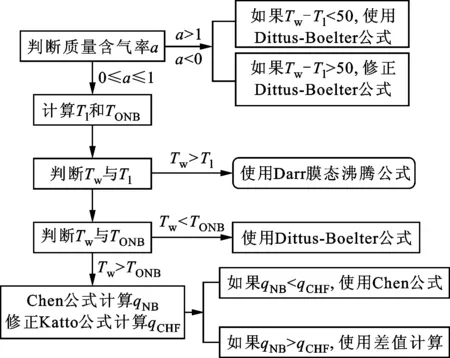
圖2 換熱模型選擇及判定條件

2 計算模型

針對低溫流體預冷真空管路過程的管壁瞬態降溫特性,采用有限容積法耦合求解管內流體流動與換熱方程,有限差分法求解管壁一維非穩態導熱方程,流體與壁面的換熱通過流型判定及多種換熱模型的恰當選用予以考慮,管壁外側輻射漏熱進行線性化離散處理。

2.1 離散化處理

將管路內流體沿長度方向劃分節點,管壁沿長度方向和徑向均劃分節點,離散節點分布如圖3所示,其中qcov表示壁面與流體之間換熱量。流體流動換熱采用有限容積方法進行計算,將含有四次項的輻射熱進行泰勒展開,并采用有限差分的方法計算管壁非穩態導熱,利用準穩態換熱的方法將流固換熱以及外界環境漏熱進行耦合求解。

熱力學含氣率x計算式為

式中:γi為節點i處的焓值;γl,sat為飽和液焓;γlv為當前壓力下的相變潛熱。

每一時刻的流體節點處焓值γi計算式為

γi=γi-1+4qi-1/(πd2G)

式中:γi-1為上一節點焓值;qi-1為上一節點處流體與壁面換熱量。

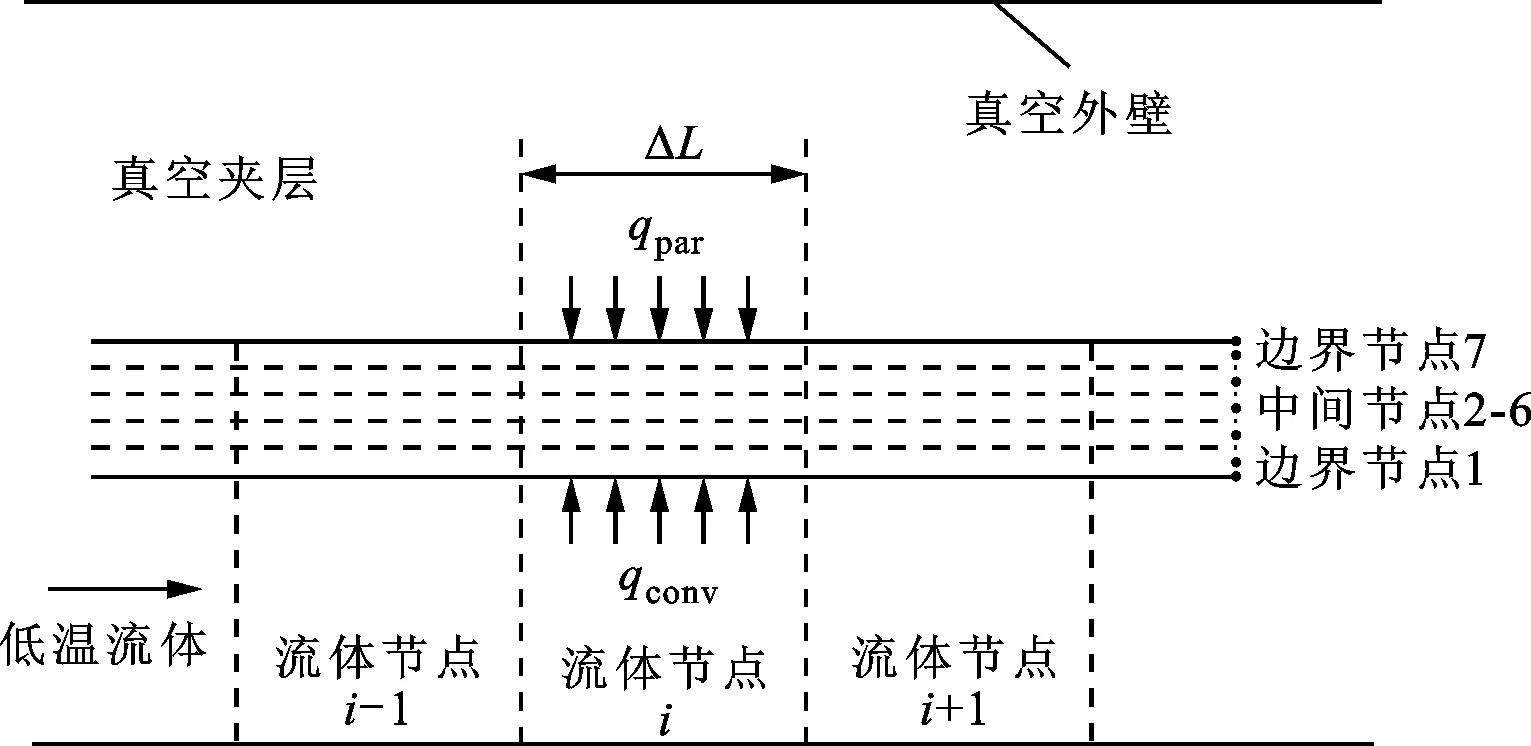
圖3 數值模擬離散節點分布

2.2 耦合換熱計算

在低溫流體預冷真空管路過程中,首先應該判斷各節點低溫流體與壁面的傳熱工況,確定流體與壁面間換熱量,進而計算出節點處的溫度、流速及含氣率等流動參數,并計算管壁的溫度分布,程序流程如圖4所示。

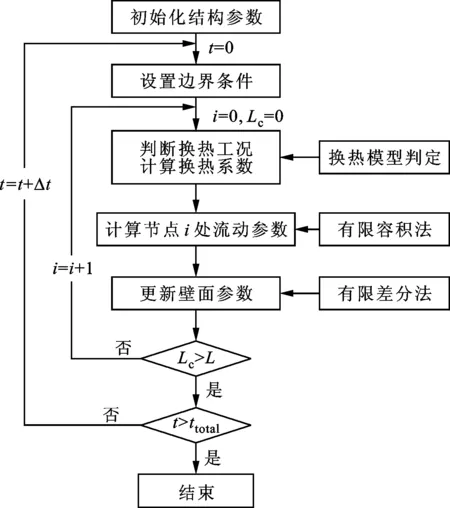
圖4 程序流程圖

2.3 模型驗證

基于上述計算模型,對文獻[9]和文獻[22]中液氮預冷真空管路的9個實驗工況開展計算分析,實驗條件如表2所示,其中流動方向包括水平和豎直向下兩個方向,9個實驗工況的質量流速各不相同。

9個實驗工況中預冷時間的實驗數據與計算結果的對比情況如圖5所示,由圖9可知,對預冷時間的預測誤差在10%之內,說明本文建立的預冷模型具有較高精度,可用于液氮和液氧(兩者物性非常接近)預冷管路的模擬計算中。

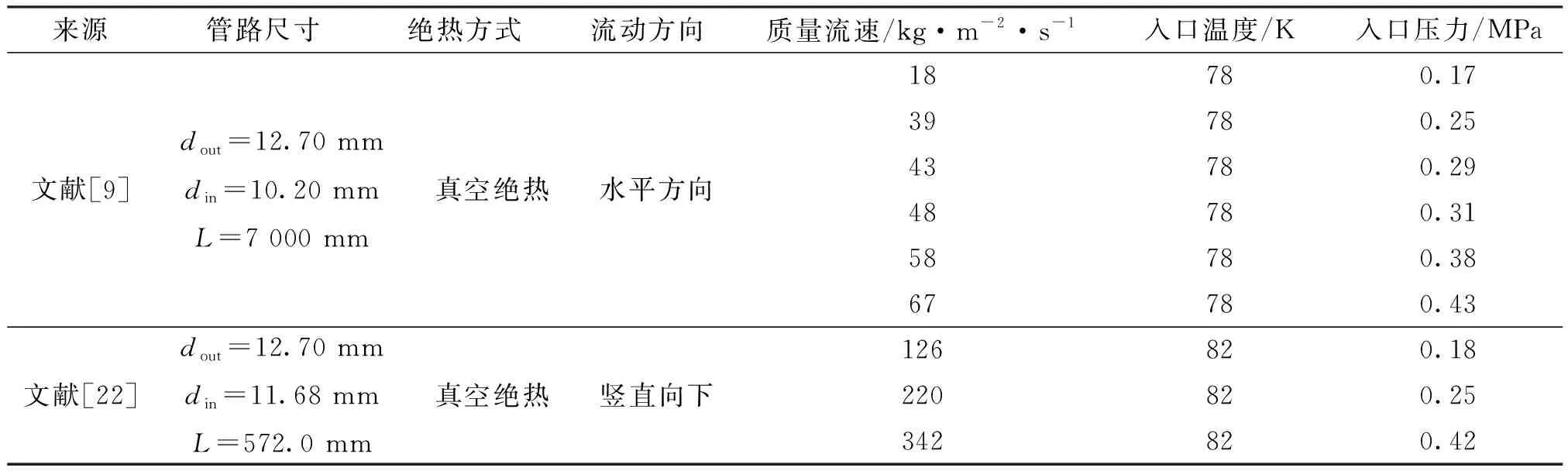
表2 管路預冷實驗工況條件

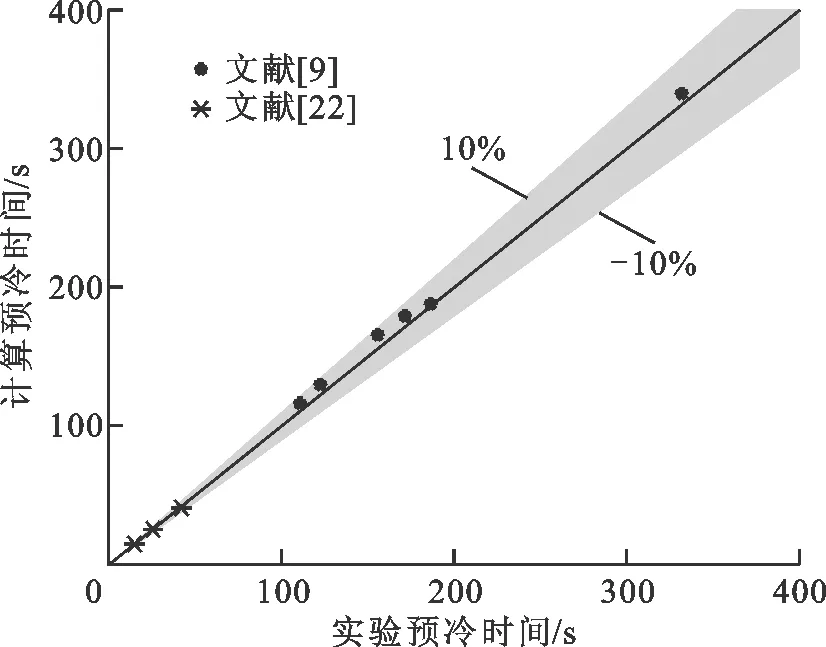
圖5 實驗數據與計算結果對比

3 管路預冷流型與換熱預測及分析

針對文獻[9]中G=43 kg/(m2·s)的實驗工況,對管路預冷過程中換熱特性及流型分布進行預測。

3.1 流型與換熱特性分析

70 s時刻管路預冷流型和換熱特性情況如圖6所示。由圖6可知:在70 s時,沿管長方向流型依次為單相液、泡狀流、反環狀流、單相氣,發生的換熱方式依次為單相液體強制對流、核態沸騰、過渡沸騰、膜態沸騰及單相氣體強制對流;核態沸騰和過渡沸騰換熱系數遠大于其他換熱方式,發生核態和過渡沸騰時,管路中的含氣率迅速增大,同時核態、過渡沸騰換熱區域遠小于膜態沸騰換熱區域。

3.2 管壁非穩態溫降特性

管路監測點處流體與壁面溫度隨時間的變化情況如圖7所示。由圖7可知:首先經歷全氣相強制對流,壁面溫度和流體溫度逐漸降低,隨后進入膜態沸騰換熱,當壁面溫度降低為膜態沸騰起始溫度時,換熱方式變為過渡和核態沸騰,壁面溫度大幅降低,隨后進入全液相強制對流階段,直至預冷完成;預冷過程大部分時間為全氣相和膜態沸騰階段,大約占預冷時間的95%以上,核態沸騰和過渡沸騰持續時間很短。

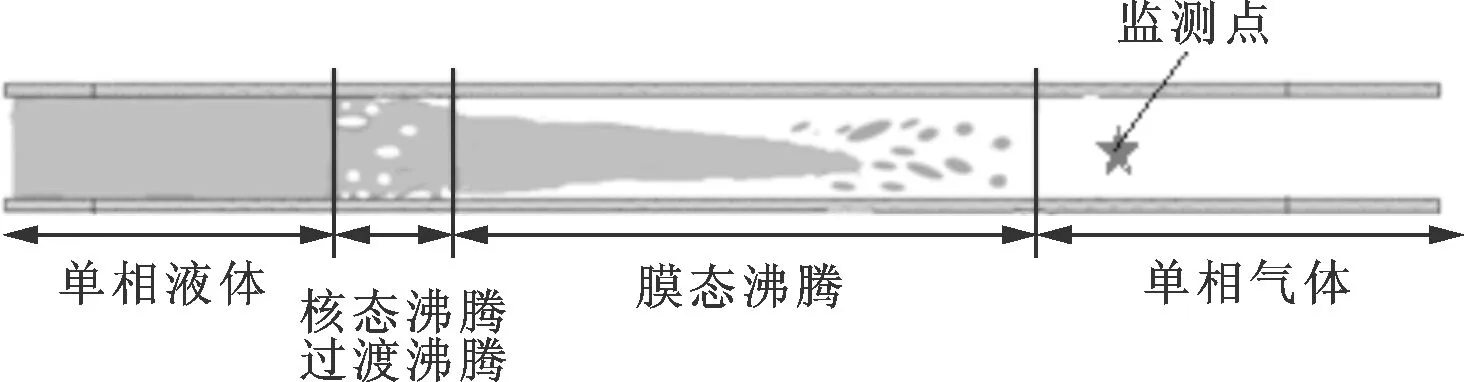
(a)管路預冷流型分布

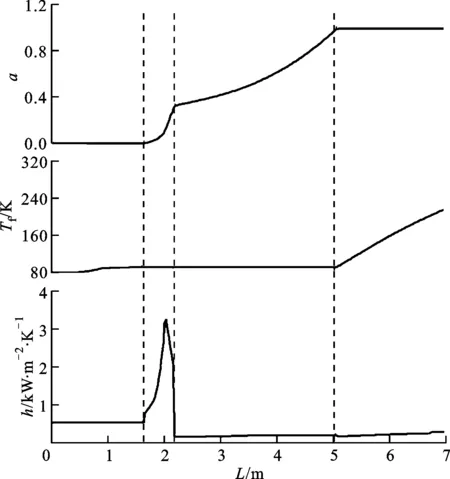
(b)換熱特性分布圖6 典型時刻管路預冷流型分布及換熱特性

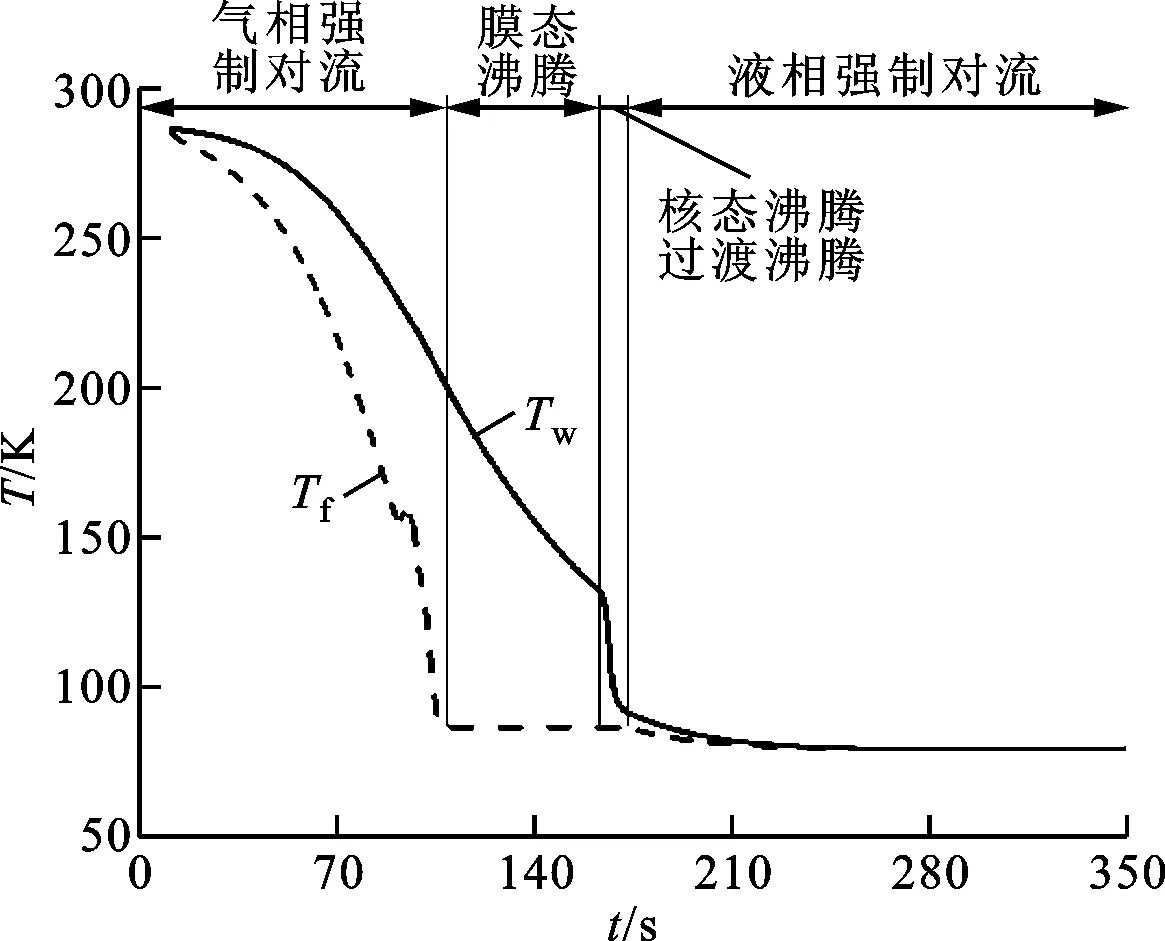
圖7 特定位置處流體與壁面溫度隨時間變化規律

進一步分析整個管路壁面降溫特性,沿管路長度方向不同位置處流體溫度隨時間變化情況和壁面溫度隨時間變化如圖8、圖9所示。每個區域中壁面溫度隨時間及位置以相同規律變化,這是因為相同的換熱區域具有相近的換熱特性。

此外,距離管路入口2 m內的管路區域,主要發生膜態沸騰,膜態沸騰換熱將壁面溫度冷卻至約130 K,之后核態和過渡沸騰將壁面冷卻至流體溫度附近。距入口2 m之后的管路區域,先經歷氣相強制對流,壁面溫度降至200 K左右,之后發生膜態沸騰換熱,壁面降至130 K附近,最后發生核態、過渡沸騰。由圖9可知,壁面溫度降低過程的換熱量主要通過氣相強制對流換熱和膜態沸騰,約占總換熱量75%。

圖8 流體溫度隨時間變化規律

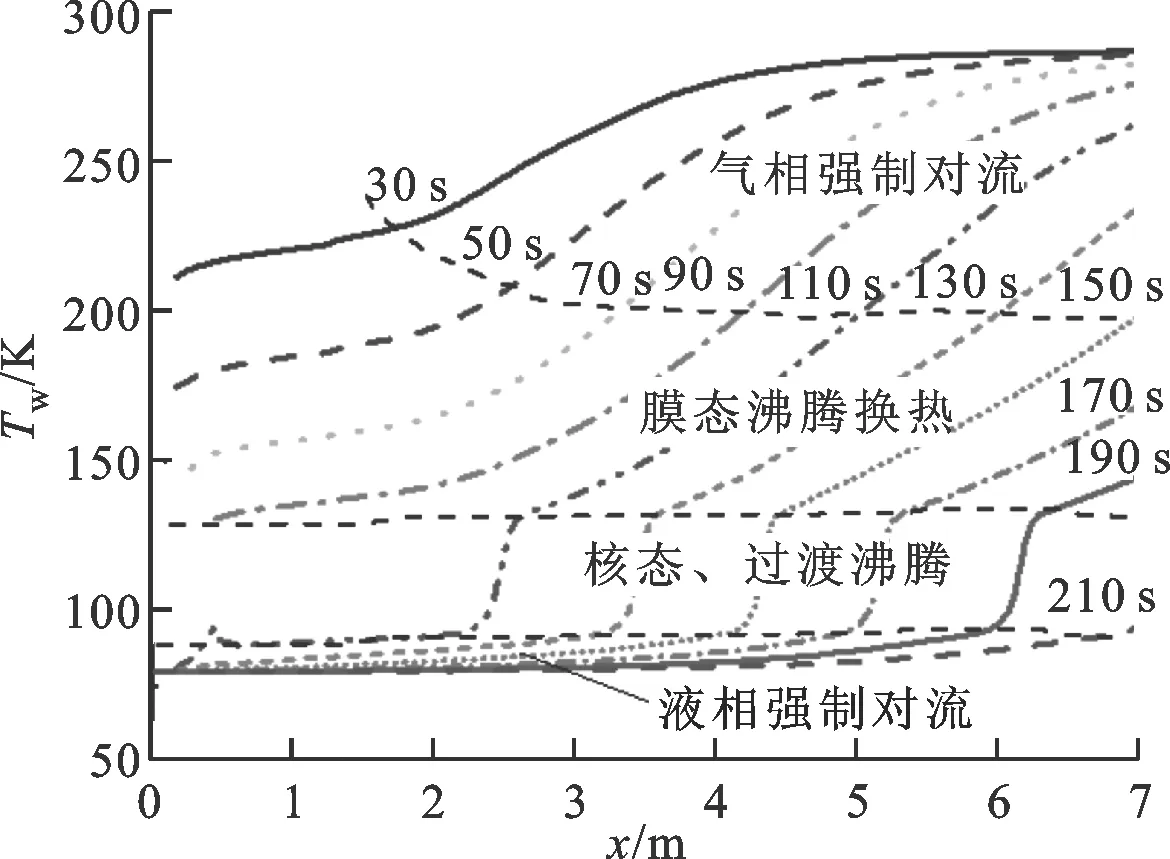
圖9 壁面溫度隨時間變化規律

3.3 質量流速影響分析

為縮短預冷時間同時減少推進劑消耗量,以長度為10 m的管路為模型,將質量流速對預冷過程的影響進行計算分析。質量流速在50 kg/(m2·s-1)和500 kg/(m2·s-1)的范圍內,預冷完成時間隨質量流速的變化情況如圖10所示。由圖10可知,質量流速越大,預冷完成時間越短,在低質量流速范圍內,預冷完成時間隨質量流速的增加而急劇降低,當質量流速增加到一定程度后,預冷完成時間趨于平穩。因此,預冷過程中存在一個最優質量流速,既可以縮短預冷時間,同時也可以減少推進劑的浪費。

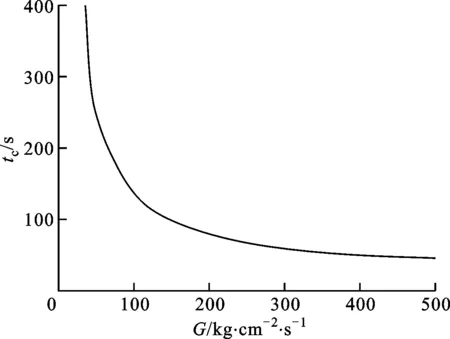
圖10 不同質量流速條件下的預冷時間

4 結 論

通過對低溫流體預冷管路過程進行計算分析,本文得到如下結論:

(1)本文建立的低溫流體預冷真空管路的非穩態計算模型,考慮了預冷過程中多種換熱方式,在開展低溫流體預冷管路過程預測時具有較高精度,對預冷時間預測的誤差在10%之內;

(2)在低溫流體預冷管路過程中,不同換熱方式的換熱情況差異很大,其中核態沸騰與過渡沸騰換熱方式的換熱系數與其他換熱方式相比約大一個數量級;

(3)在低溫流體預冷管路過程中,大部分時間的換熱方式為單相氣強制對流和膜態沸騰,約占總預冷時間的95%,總換熱量的75%,核態和過渡沸騰發生時間較短;

(4)質量流速是影響預冷完成時間的重要因素,在低質量流速時,預冷時間隨質量流速的增加而迅速降低,當增加到一定程度時,預冷時間趨于平穩。