求解滑移流區外掠圓柱體氣流流動與傳熱特性的數值模型

謝福壽,雷剛,邱一男,徐元元,王天祥,厲彥忠

(1.航天低溫推進劑技術國家重點實驗室,100028,北京;2.西安交通大學能源與動力工程學院,710049,西安)

近年來,關于稀薄氣體流動與傳熱問題日益受到人們的關注,最典型的4類案例為:①運載器穿過大氣層或再入大氣層的氣動加熱[1];②火星登陸器熱設計和熱管理[2];③微小精密熱線風速儀研制[3];④高速真空隧道內列車儀表的熱設計和熱管理[4]。對于運載火箭升空,隨著大氣密度的逐漸減小,氣體的稀薄效應開始凸顯,連續介質假設逐漸失效,此時氣體流態會依次經歷連續流區(Kn<10-2)、滑移流區(10-210),如圖1所示。目前,由于稀薄氣體流動復雜,致使無法采用統一的算法或方程進行描述,故每個流態的求解方法不盡相同。

(a)不同特征長度下氣體流態劃分

(b)不同馬赫數和雷諾數下氣體流態劃分圖1 運載火箭穿越大氣層時氣體流態隨大氣高度的分布

滑移流區是指氣體與氣體之間的碰撞頻率,雖然其比氣體與物體表面間的碰撞頻率高相當多,但稀薄效應已不能再忽略,在靠近壁面處的非平衡效應開始占主導作用,此時氣體流動與傳熱會呈現出兩個典型的特征:①速度滑移;②溫度跳躍。為了充分反映出該流域的典型特征,許多研究者采用壁面邊界條件修正的CFD技術進行流動與傳熱研究[5-10]。Kishore等通過速度滑移和定壁溫邊界條件修正對牛頓流體外掠球形顆粒的傳熱現象進行了數值仿真[5-6]。Choi等開發了嵌入Maxwell滑移邊界條件的非結構化網格N-S方程求解模型,對圓柱體表面的速度滑移和溫度跳躍進行了研究[7]。索曉娜等采用連續介質流動方程與壁面速度滑移和溫度跳躍邊界條件相結合描述微通道內稀薄氣體二維可壓縮滑移流動[10]。Xie等對滑移流區稀薄空氣外掠圓柱體流動與傳熱特性展開了研究,其雷諾數范圍為0.001～20,克努森數范圍為0.01～0.1[11]。雖然許多學者針對滑移流區采用N-S方程進行了一定的研究,然而都沒有考慮壁面曲率對速度滑移和溫度跳躍的影響以及滑移邊界方程與CFD求解器之間坐標系的轉換。Lockerby指出在目前稀薄氣體流動中,Maxwell最初滑移邊界條件被廣泛地誤用,其認為假如采用通用滑移邊界來模擬帶曲率的壁面問題時,一些關鍵的物理現象就會丟失:①通用滑移邊界條件計算出的切向滑移速度明顯低于Maxwell最初滑移條件得出的;②對于帶曲率的彎頭通道,采用Maxwell最初滑移邊界可以預測速度逆流現象,而通用滑移邊界條件則不能預測該流動行為;③對于外掠一個理想光滑球體,假定所有的入射分子都發生鏡面反射,即α=0,則采用Maxwell最初滑移邊界推導的Basset阻力方程預測表面摩擦阻力系數應該為0,但采用通用滑移邊界條件推導的方程預測結果為負值,出現了非物理解[12]。

課題組前期搭建了一套低密度風洞試驗裝置,開展了大量的實驗研究,獲得了一些有價值的研究結果[13-14]。然而,這些實驗結果并不能形象地展示出流場和溫度場的變化規律。當克努森數增加時,也不能獲得壓力系數和傳熱系數沿圓柱體壁面變化的規律,更不能揭示流體掠過圓柱體流動與傳熱的機理。同時,由于實驗條件的限制,對總結出的經驗關聯式,其雷諾數使用范圍仍然比較窄。因此,有必要開發新的數值模型來深入研究滑移流區流體流動與傳熱問題。

為了精確預測滑移流區稀薄氣體流動與傳熱問題,本文擬基于有限容積法的ANSYS FLUENT 18.0平臺,開發一套可用于該流域氣體外掠圓柱體流動與傳熱仿真的數值模型,其考慮壁面曲率的影響,解決了CFD求解器中一些關鍵性技術問題,如坐標變換、UDF開發、UDF植入、求解發散等。在此基礎上,與課題組之前實驗數據進行詳細的對比驗證,充分驗證數值模型的可靠性和精確度,為計算流體動力學實現滑移流區氣體流動與傳熱問題研究構建一座橋梁。

1 數值模型構建

本文所研究的問題為稀薄氣體外掠圓柱體,直徑為D,流態區域尺寸及坐標如圖2所示。圓柱體壁面溫度定義為Tw,空氣與圓柱體之間的溫度跳躍和速度滑移定義為Ts和us。

圖2 計算區域與邊界條件示意圖

1.1 層流N-S控制方程

對于滑移流區,氣體橫掠圓柱體在主流區的流動和傳熱現象可由N-S方程和能量方程來描述,其中二維、層流、不可壓縮流體的無量綱表達式如下

(1)

(2)

(3)

(4)

式中:u*、v*分別為x、y方向的無量綱速度分量;p*為無量綱壓力;T*為無量綱溫度。

無量綱變量定義為

式中:u、v分別為x、y方向速度分量;u∞為自由流速度;p為空氣壓力;ρ∞為氣體密度;T為氣體溫度;T∞為自由流溫度;Cp為壓力系數;p∞為自由流靜壓力;Cf為表面摩擦系數;τw為壁面剪切力。

1.2 邊界條件

滑移流區氣體橫掠圓柱體流動與傳熱問題的邊界條件如圖2所示,詳細設置如下。

在計算區域左側,均勻的速度入口邊界條件和氣體溫度設置為

u*=1;v*=0;T*=0

在計算區域右側,默認氣體在出口處為充分發展狀態,壓力出口邊界條件和空氣溫度設置為

沿著計算區域頂端和底端,壁面設置為移動壁面,速度等于入口速度,即

u*=1;v*=0;T*=0

在圓柱體壁面,速度滑移表達式以速度分量的形式植入到移動壁面中,其具體的表達式為[15]

(5)

式中:un為壁面法向的氣體速度;n為壁面法向的坐標;s為壁面切向的坐標;σm為動量協調系數,具體取值見1.3小節;Lm為氣體分子平均自由程。方程(5)右側第1項是一階等溫速度滑移,由圓柱體壁面處的切向應力推導而來,而第2項是由于切向溫度梯度引起的一個熱蠕動。需要說明的是,在帶曲率的物體中應將導數項?un/?s考慮進去,然而在大多數已公布的工作中,該項要么被忽略,要么被導數項?us/?s錯誤地取代。Lockerby研究發現,將導數項?un/?s代入滑移邊界方程之中,對于越稀薄的氣體,計算越準確[12]。

溫度跳躍的表達式以壁面溫度修正的形式植入到壁面中,其具體的表達式為

(6)

式中:a為熱協調系數,具體取值見1.3小節。

1.3 壁面邊界條件滑移修正

速度滑移邊界條件以一個移動壁面速度的形式加入,而溫度跳躍的邊界條件則以一個修正的定壁溫形式添加。該UDF采用C語言來編寫,以編譯的形式在Fluent求解器中執行,其中所涉及到的速度梯度和溫度梯度分別從求解器中抽取,而速度滑移和溫度跳躍根據方程(5)(6)計算得到。

由于圓柱體表面存在曲率,所以自然坐標系與求解器中默認的笛卡爾坐標系是不統一的,正如圖3所示。為了表達自然坐標系(s,n)中速度向量和所有的導數項,必須進行坐標變換。笛卡爾坐標系(x,y)中速度向量和所有的導數項可以從Fluent求解器中抽取。在坐標變換之前,首先必須確定在壁面每個單元上兩個坐標系之間的夾角θ。根據空間向量的性質,通過余弦函數則可以給出θ的表達式

(7)

式中:A=-An為邊界單元面積的法向向量,由Fluent?求解器提供;i、j為沿著x、y方向的單位向量。

圖3 在壁面處笛卡爾坐標系與自然坐標系及速度分量

使用鏈式法則,可將方程(5)(6)的導數項表示為

(8)

(9)

(10)

(11)

自然坐標系與笛卡爾坐標系關系如下

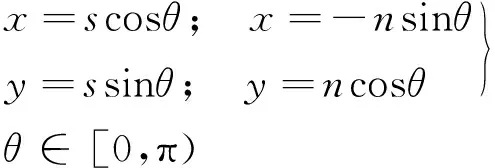
(12)

在s、n方向對x、y分別求偏導數的表達式為

(13)

在笛卡爾坐標系和自然坐標系中,向量u可分別表達為

uxi+uyj

(14)

usk+ung

(15)

式中:k和g為s、n方向上的單位向量。

根據幾何關系,如4所示,可獲得向量(i,j)和(k,g)之間的關系如下

(16)

(a)自然坐標系對i的表達 (b)自然坐標系對j的表達圖4 單位向量變換

最后,將方程(16)代入方程(14),化解整理后,即可得到(ux,uy)和(us,un)之間的關系為

u=(uxcosθ+uysinθ)k+(-uxsinθ+uycosθ)g

(17)

于是

(18)

將方程(13)(18)代入方程(8)～方程(11),所有的導數項即可整理為

(19)

(20)

(21)

(22)

通過訪問ANSYS Fluent求解器中的數據內存,可獲得速度和溫度的全部偏導數項(?ux/?x,?ux/?y,?uy/?x,?uy/?y,?T/?x,?T/?y)。對于角度偏導數(?θ/?x和?θ/?y),則需要通過極坐標系來確定。

如圖5所示,笛卡爾坐標系中(x,y)與極坐標系中(r,θ)之間的關系可依據幾何關系來表示

(23)

式中r為圓的半徑。于是,角度偏導數可表示為

(24)

圖5 笛卡爾坐標系與極坐標系之間的變換

需要說明的是,動量協調系數σm和熱協調系數a一般取決于許多因素,如氣體與物體表面材料的種類、壁面光滑度、表面的清潔程度(氧化程度、是否有污染物覆蓋、是否吸附其他氣體)、溫度、壓力等以及一些尚未被人們知曉的因素,且兩個系數都在0(鏡面反射)到1(漫反射)之間變化。根據文獻[16-17]報道,對于大多數工程應用來說,這兩個系數都非常接近于1,故在目前的工作中這兩個系數都取為1。

1.4 CFD數值計算方案確定

采用商業計算流體動力學代碼——ANYSYS Fluent展開數值仿真,即聯合邊界條件求解控制方程(1)～方程(4),最終獲得了稀薄氣體外掠圓柱體的壓力場、速度場和溫度場。空間離散梯度方案選擇基于單元最小二乘法梯度,壓力離散方案選擇二階格式,動量方程和能量方程離散方案選擇二階迎風格式。在Fluent中,默認收斂標準是足以用來判斷收斂的,即連續方程和動量方程的全局殘差均降到了10-11,而能量方程的全局殘差降到了10-15,則認為迭代收斂。

2 結果討論與分析

2.1 連續流低壓狀態下定克努森數結果比較

圖6展示了連續流區低壓狀態下無滑移邊界數值預測值與滑移邊界數值預測值的比較結果,其中低壓狀態的壓力為50 kPa,所對應的克努森數為0.006。從圖中對比可知,只要氣體流態處于連續流區時,無論是常壓狀態還是低壓狀態,無滑移邊界與滑移邊界的計算結果都非常相近,兩者相對誤差在1.5%以內。

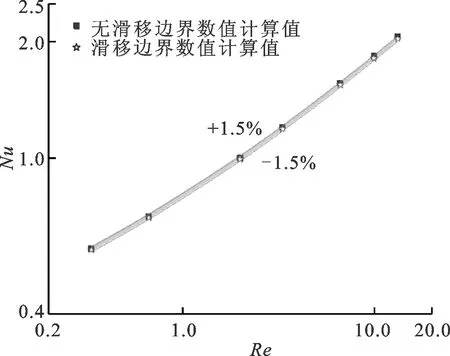
圖6 連續流區數值計算結果

2.2 滑移流區低壓狀態下定克努森數結果比較

圖7呈現了在滑移流區狀態下無滑移邊界數值預測值、滑移邊界數值預測值和實驗結果的對比。滑移流區低壓狀態分別是指氣壓壓力為6 kPa和3 kPa,所對應的克努森數分別為0.054和0.108。從圖中可看出,當氣體流態由連續流區進入到滑移流區后,采用無滑移邊界條件的計算結果與實驗結果的誤差已達到±15%,尤其是壓力越低,克努森數越大,計算誤差越大。即使在同一壓力下,采用無滑移邊界條件的計算結果與實驗結果的誤差也會隨著雷諾數增大而增大。采用滑移邊界條件的計算結果可將誤差控制在±2.5%以內,所以在稀薄氣體滑移區的流動換熱問題中,本文修正的滑移流區數值模型可保障數值計算的準確性。

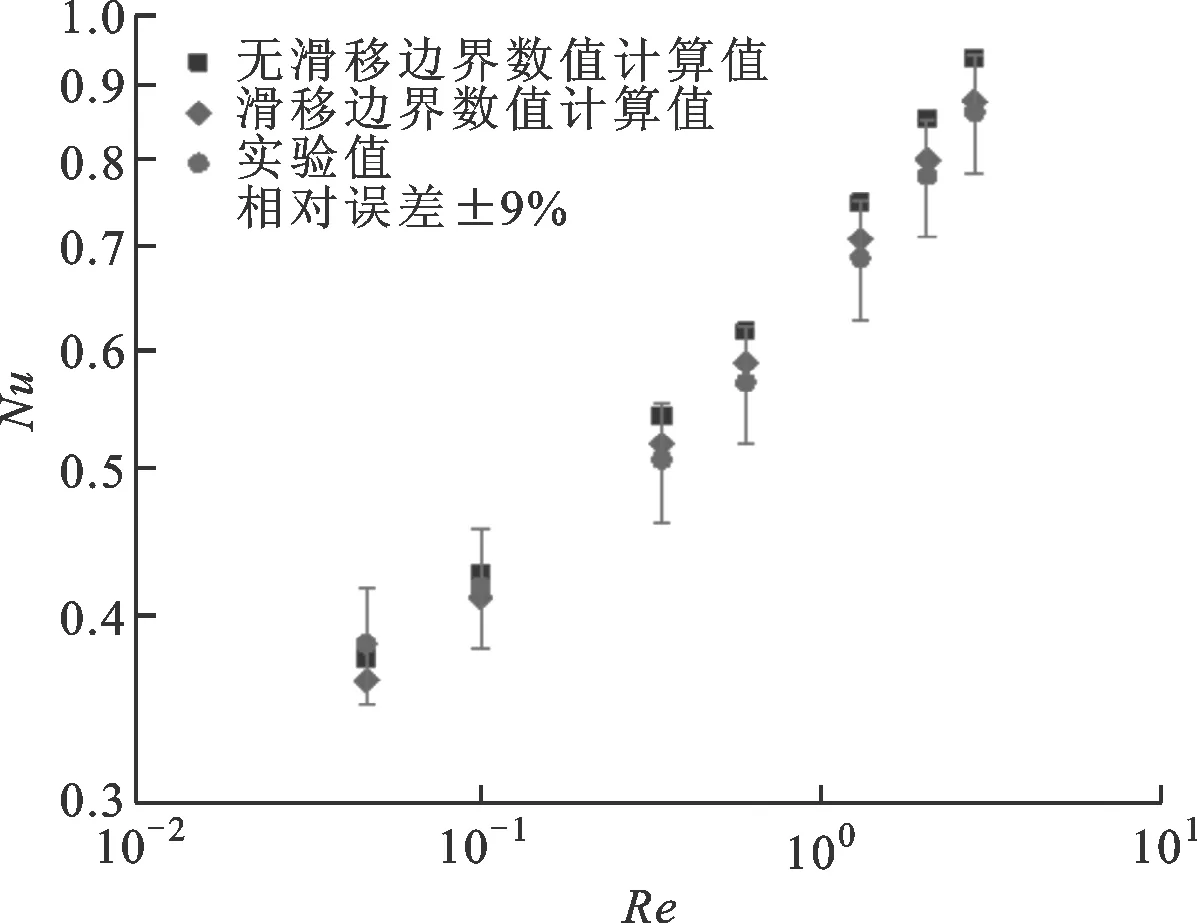
(a)6 kPa

(b)3 kPa圖7 滑移流區數值計算結果

2.3 過渡流區低壓狀態下定克努森數結果比較

圖8給出了過渡流區狀態下無滑移邊界數值預測值、滑移邊界數值預測值和實驗結果的對比。過渡流區低壓狀態是指氣體壓力為1 kPa,所對應的克努森數為0.323。從圖中可看出,當低壓氣體的流態處于過渡流區時,采用無滑移邊界條件的計算結果與實驗結果的相對誤差已達到±60%,即使采用滑移邊界條件修正,也只能將相對誤差縮小到±20%以內。

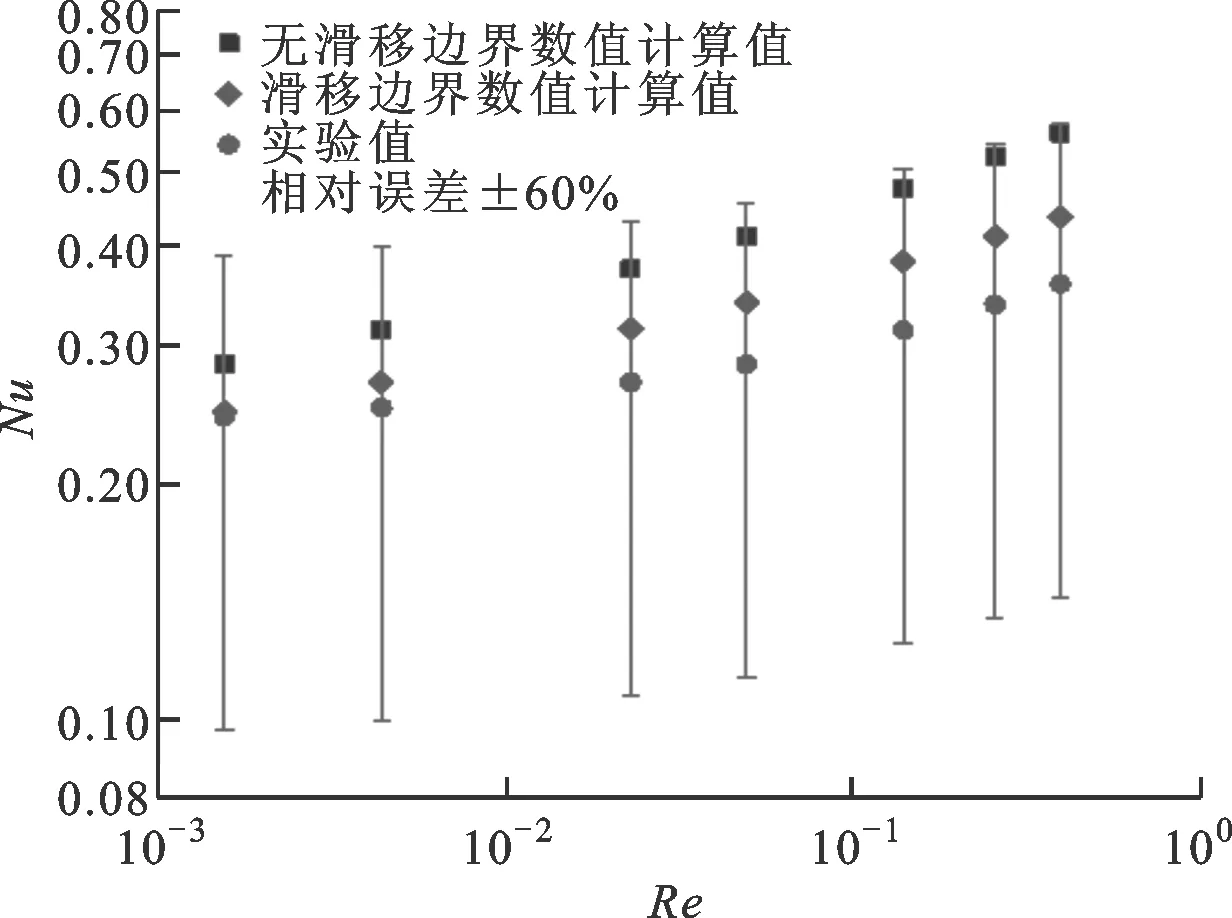
圖8 過渡流區數值計算結果

2.4 跨流域變克努森數結果比較

為了進一步驗證該數值模型的可靠性和精確度,維持氣體速度(3 m/s)不變,通過改變氣體壓力,使壓力在100 Pa～100 kPa之間變化,獲得了數值預測值、實驗值,并與傳統經驗關聯式(Fand[18],Hilpert[19],McAdams[20],Collis[21])預測值進行了比較,如圖9所示。從圖中可清楚地看到,在連續流區,數值計算結果與本文實驗值、Collis的經驗關聯式預測值和Fand的經驗關聯式預測值都吻合良好,說明數值計算過程都是合理的,包括邊界條件設置、求解方法選擇、物性設置、區域無關性研究和網格無關性研究等。

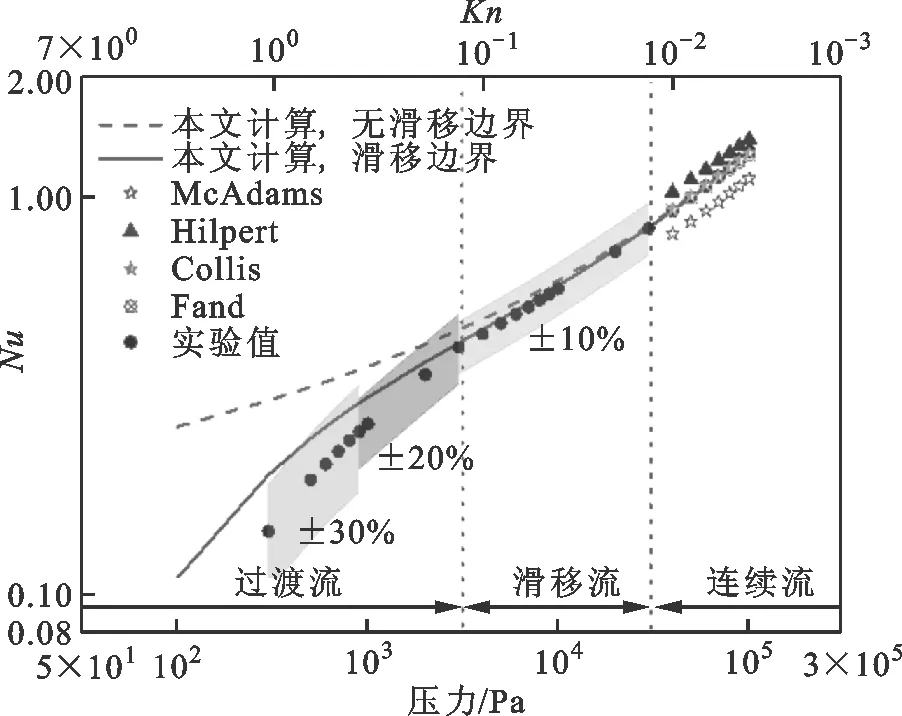
圖9 跨流域變克努森數結果比較

在滑移流區,采用滑移邊界條件修正的數值計算結果與本文實驗值吻合良好,其最大相對偏差處于±2.5%以內,而采用無滑移邊界條件的數值計算結果逐漸偏離實驗值,最終達到10%的相對偏差。也就是說,通過滑移邊界條件修正,數值計算結果的精度有了顯著提升。

在過渡流區,采用滑移邊界條件修正的數值計算結果與本文實驗結果相比,計算偏差逐漸增加,而采用無滑移邊界條件的數值計算結果則完全偏離了本文實驗結果,因此在該流態下,數值計算模型需要進一步修正。然而,本文側重于滑移流區低壓空氣外掠圓柱體流動與傳熱特性研究,所以在此不考慮過渡流區。

2.5 滑移效應對低壓氣體外掠圓柱體的流動影響

圖10展現了在滑移流區當雷諾數為1時無量綱滑移速度沿圓柱體壁面的分布規律。從圖中可看出,當克努森數保持不變時,無量綱滑移速度在前止滯點處為0,隨著角度α的增加,其逐漸增加到某一最大值,然后開始減小,直到在后止滯點處變為0。因為在前止滯點處,空氣動壓轉變為靜壓,使速度變為0。隨后,靜壓會逐漸再次轉變為動壓,使壁面的切向速度最終達到一個最大值。由于稀薄效應的影響,最大無量綱滑移速度會隨著克努森數的增加而增大,當克努森數達到0.1時,最大無量綱滑移速度可達到自由來流速度的16%。

圖10 無量綱滑移速度沿圓柱體壁面的分布

圖11描述了在滑移流區雷諾數為1時壓力系數沿圓柱體壁面的分布規律。當克努森數保持不變時,壓力系數最大值位于圓柱體前止滯點處,且沿著圓柱體壁面逐漸減小。然而,由于滑移效應的影響,圓柱體前止滯點處的壓力系數會隨著克努森數的增加而逐漸減小,不過克努森數對壓力系數的影響其實并不大。

圖12 表面摩擦系數沿圓柱體壁面的分布

圖12描述了在滑移流區雷諾數為1時表面摩擦系數沿圓柱體壁面的分布規律。從圖中可知,當克努森數一定時,由于雷諾數較低,黏性力起主導作用,從而抑制邊界層分離,使圓柱體前止滯點與后止滯點速度為0,故表面摩擦系數沿著圓柱體壁面先從0增加至最大值,然后逐漸減小至0。由于稀薄效應影響,最大表面摩擦系數隨著克努森數增加而逐漸減小,當克努森數達到0.1時,最大表面摩擦系數比連續流區最大表面摩擦系數減小了38%。

3 結 論

針對滑移流區氣體外掠圓柱體問題,構建了一套預測低壓氣體流動與傳熱的數值模型,考慮了軸向溫度梯度引起的熱蠕動影響和壁面曲率的影響,通過與實驗數據對比,得出以下結論:

(1)當氣體流態處于連續流區時,滑移邊界修正模型的計算結果與無滑移邊界的計算結果相近;

(2)當氣體流態處于滑移流區時,預測外掠圓柱體傳熱的傳統經驗關聯式已不再適用,此時采用滑移邊界修正的數值模型,可實現對稀薄氣體滑移流區流動與換熱的精確預測,且數值計算結果明顯優于傳統經驗關聯式預測結果;

(3)在滑移流區,稀薄效應對低壓氣體外掠圓柱體的流體動力學特性影響顯著,隨著克努森數增加,最大無量綱滑移速度呈線性增加,而最大表面摩擦系數呈現線性減小。