高中數學文化教育在引言課中的實施策略初探①——以“平面解析幾何引言課”為例

王克亮

(江蘇省射陽中學 224300)

數學文化通常包括數學史，數學的精神、思想和方法，數學的語言，數學的應用等方面，數學文化教育應貫穿整個高中教學過程之中. 引言課通常設置在一個章節的起始，側重回答“這個內容是什么？為什么要學習這個內容？如何學好這個內容？”等問題. 那么，如何在引言課中實施數學文化教育呢？筆者擬以近期開設的“平面解析幾何引言課”這節省公開課為例，談談自己的一些膚淺實施策略.

1 回顧形成歷史，揭示研究思想

高中數學的每一塊知識內容都蘊含著一些研究思想，這些研究思想應該是教學中深植學生骨髓的東西，能對學生的終生發展起著潛移默化的作用. 那么，在引言課中如何將這些研究思想自然地揭示出來呢？筆者認為，回顧知識形成歷史，沿著前人的思路行走是一個較好的策略.

在平面解析幾何引言課中，筆者就是從數學史談起的.

話題關于平面解析幾何，你現在最想了解的是什么？

根據學生的回答整理成如下三個問題：(1)是什么？——平面解析幾何是一門怎樣的學科？(2)為何學？——為什么要學習平面解析幾何？(3)怎么學？——怎樣才能學好平面解析幾何？

平面解析幾何是一門怎樣的學科呢？對這個問題的回答得從數學史談起.在數學史上，曾經有這么幾位數學家，他們雄心勃勃，想創造一種能夠解決世界上一切問題的方法，法國著名數學家笛卡爾就是其中一位. 他們的設想是這樣的:“任何問題→數學問題→代數問題→方程問題→求解方程→得到結論”.那么，對于幾何問題，該如何用代數的方法來解決呢，這是他們遇到的難題之一.

據說，后來有一天，當笛卡爾躺在床上休閑時，忽然他看到墻角的蜘蛛網上有一只蜘蛛在爬來爬去，便突發奇想，假如在墻角的三根交線上分別標上刻度，不就能用有序的數對來表示蜘蛛的位置了嗎！這正是直角坐標系的芻形. 有了直角坐標系，點就可以用數來表示，進而線與面也能用數來表示，這樣用代數的方法來研究幾何問題有了可能,從而使得代數與幾何兩者相互結合而共同發展，產生了解析幾何學.

所以，解析幾何學是一門用代數的方法來研究幾何問題的學科. 在中學教材平面解析幾何當中，將要研究直線、圓、圓錐曲線(橢圓、雙曲線和拋物線)等曲線的代數表示及幾何性質.

評注本節課是從發生在數學家笛卡爾身上的一個小故事開始的，自然地回顧了數學史知識，既激發了學生的聽課興趣，又揭示了本章的研究思想，能給學生留下較為深刻的印象.

2 點擊核心概念，感悟數學語言

數學語言是數學思維的載體，是數學理論的基本構成成分，所以數學文化教育離不開數學語言的感悟. 那么，如何在引言課中感悟相關的數學語言呢？筆者認為，可點擊一些核心概念，在逐步呈現中初步感受其數學表達.

筆者認為，曲線的方程與方程的曲線是平面解析幾何中的兩個核心概念，在引言課中可進行點擊，并體會其數學表述.

問題1設A(4,0),B(0,2)兩點確定的直線為l，如何判斷點Q(-2,3)是否在直線l上？

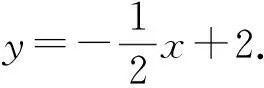
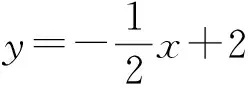
初步感受“兩都”關系.

變式設A(4,0),D(4,2)兩點確定的直線為m，如何判斷點P(x,y)是否在直線m上？

體會該直線不是函數的圖象，不能運用一次函數解析式來解決問題，并在得到關系式x-4=0后，引導學生將其改寫成x+0·y-4=0.

追問1直線m與關系式x+0·y-4=0之間符合“兩都”關系嗎？

進一步感受“兩都”關系.

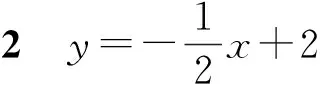
體會它們都是二元一次方程，“y=f(x)”不能包含上述全部情形，自然給出“方程f(x,y)=0”這個表示形式.

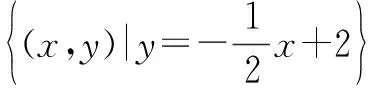
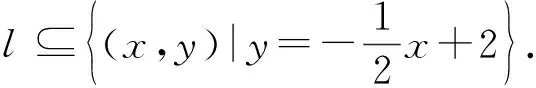
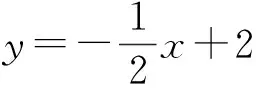
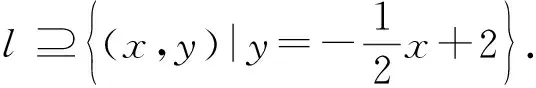
追問2“兩個都”同時成立呢？

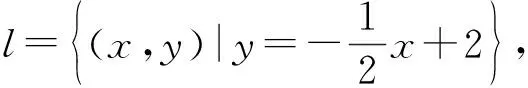
問題1.3一般地，對于曲線C與方程f(x,y)=0，當它們滿足什么條件時，可稱方程f(x,y)=0為曲線C的方程？曲線C為方程f(x,y)=0的曲線呢？

需同時滿足“兩都”關系，即(1)曲線C上任一點的坐標都是方程f(x,y)=0的解；(2)以方程f(x,y)=0的解為坐標的點都在曲線C上.

評注這里用“兩都”這一數學語言貫穿前后，從點集相等的角度闡明了“數”與“形”的等價性，展現了數學語言的科學性、嚴謹性、簡潔性和通用性.

3 力求和諧統一，展示數學之美

數學文化教育離不開數學美的熏陶，教學中如果能讓學生由衷地感受到數學之美妙，對其產生的影響將是無法估量的. 那么，在引言課中該如何展示數學之美，讓學生感受數學的魅力呢？筆者認為，深挖知識內涵，打通知識聯系，如果能把一些內在的規律用和諧統一的形式展示出來，將會給學生強烈的震撼，美感也就會隨之而來.

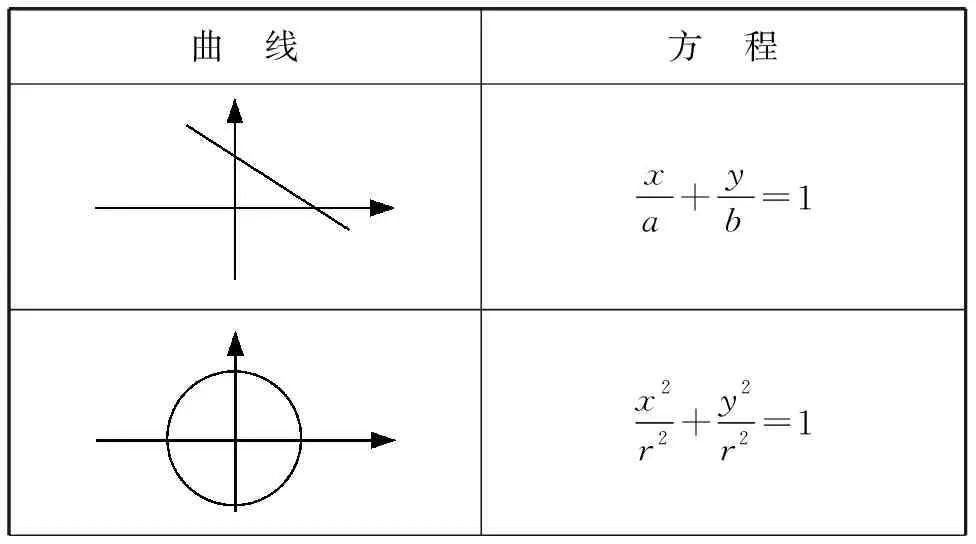
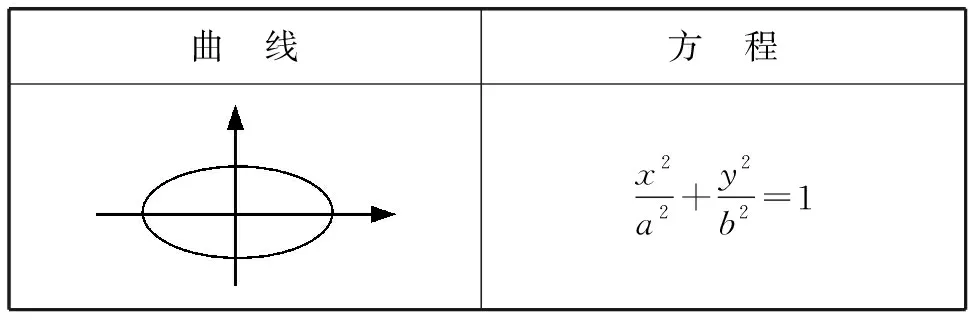
在平面解析幾何引言課中，筆者試圖將直線、圓、橢圓三者的方程用統一的形式表示出來，讓學生感受到方程的美妙.

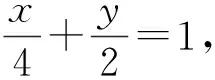
發現改寫后方程的分母就是直線在兩個坐標軸上的截距(可簡要介紹一下截距這個概念).

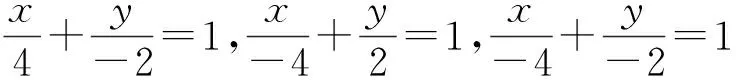
利用所給截距得到三條具體直線l1,l2,l3，并推廣到一般情形.

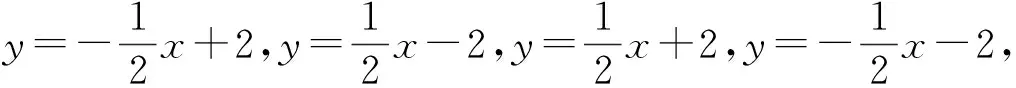
發現直線的位置關系與方程之間的聯系，并體會可用方程來研究曲線的幾何性質.

剛才實際上做了兩件事：一是將直線轉化為代數形式，得到了直線的方程；二是運用所得到的方程來研究了直線的一些幾何性質.

追問解析幾何的兩大任務是什么？

(1)建立曲線的方程；(2)運用方程研究曲線的幾何性質.

問題2以坐標原點為圓心，以r(r>0)為半徑的圓O，其方程是什么樣子的？

先得到關系式x2+y2=r2.

問題2.1圓O與方程x2+y2=r2之間符合“兩都”關系嗎？

明確x2+y2=r2就是圓O的方程.

問題2.2如何改寫圓O的方程x2+y2=r2，使得它能較好反映圓O在兩個坐標軸上的截距呢？

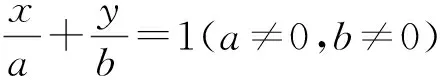
把剛才的研究結論匯總到下表內：

曲 線方 程xa+yb=1x2r2+y2r2=1

續表

從該表格中不難體會到，圖形是美觀的，方程是美妙的！

評注這里，當把直線、圓、橢圓的方程匯總在一張表格內的時候，相信學生會有“于枯燥之中見新奇”之感，激動與陶醉心情也會油然而生！

4 闡明學習意義，凸顯知識價值

數學文化的教育還應包括介紹所學知識內容的價值，讓學生消除“學了有什么用”的疑問. 那么，如何在引言課中凸顯相關知識的價值呢？筆者認為，可依據知識內容的特點從多個維度闡述學習意義，特別是其在實踐中的應用價值.

在平面解析幾何引言課中，筆者是從“刻畫效果、實踐應用、理論貢獻”這三個維度來展示《解析幾何學》的價值的.

(1)從刻畫效果看——入微

例1直線與圓的位置關系

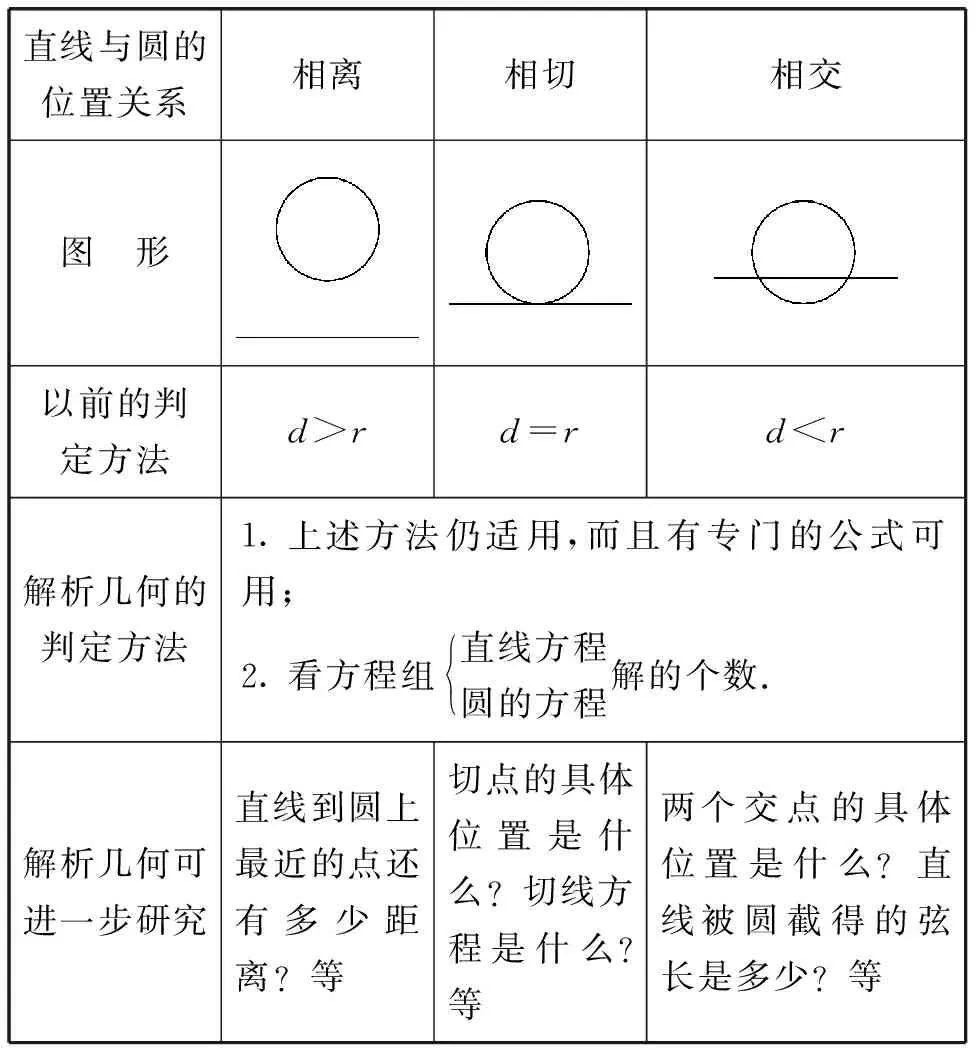
直線與圓的位置關系相離相切相交圖 形以前的判定方法d>rd=rd

解析幾何的方法對圖形及其位置關系的刻畫，實現了細微化和精確化，即入微. 先前一些被認為是幾何學中的難題，運用解析幾何的方法就變得平淡無奇了.

(2)從實踐應用看——廣泛

現實世界中，到處有美妙的曲線，對它們的精確研究往往要借助代數方程. 比如，在建造橋梁時，首先要確定橋拱的方程，然后才能進一步設計和施工；又如，在對太空的奧秘進行探索時，要把行星的運行軌道放到笛卡爾直角坐標系中，以便精確地把握它們的運行軌跡，這樣才能實現太空遨游和嫦娥登月；等等.

所以，解析幾何學在實踐中的應用非常廣泛.

(3)從理論貢獻看——巨大

對于解析幾何學的誕生，拉格朗日和恩格斯這兩位偉人都給予了高度評價(內容投影，此略).

因此，解析幾何學的誕生，其理論貢獻巨大.

總之，平面解析幾何的學習，對于轉變我們的數學觀念、拓展我們的數學思維、提升我們的數學能力、培養我們的數學素養，都有著十分重要的意義.

評注從多個維度闡明學習的理由與意義，可充分展示知識的價值.

5 進行學法指導，聚焦核心素養

數學文化教育的目的是培養學生的學科核心素養，激發學生的學習興趣與熱情，提升學生的學習信心. 那么，如何在引言課中實現這些目標呢？筆者認為，可依據相關知識個性，立足學科核心素養的提升來給予學法指導.

在平面解析幾何引言課中，筆者是站在數學建模、數學運算這兩個學科核心素養的角度進行學法指導的.

(1)建立好兩種數學模型

一是方程模型，這是從形到數的過程. 當遇到與圖形有關的問題時，要有這樣的意識，即可以通過建立直角坐標系，把圖形用方程來表示，進而利用代數運算來解決問題.

二是軌跡模型，這是從數到形的過程. 一方面，當看到代數式的時候，要有這樣的意識，想一下它會不會表示什么圖形？有沒有什么幾何意義？另一方面，當看到與動點運動相關的問題時，要善于把握它的軌跡.

例2設A,B是兩個定點，當動點P滿足下列條件時，它的軌跡是什么圖形？

(1)PA=PB；(2)∠APB=90°；(3)PA=λPB(λ>0,λ≠1)；(4)PA+PB=k(k>AB).

簡析答案(此略).

在建立好兩個數學模型的基礎上，逐步培養一種思想，叫“數形結合”；最終形成一種觀念，即“形數合一”.

(2)磨練好數學運算能力

運用代數方法來研究幾何問題，離不開繁瑣的運算，所以一定要在運算能力的培養上下功夫. 努力做到：消除畏繁情緒——敢算，掌握一般方法——會算，把握運算規律——善算.

評注相信學生能夠從該教學片斷中初步感悟到平面解析幾何這門課的特點，并從中獲得一些學習啟示，增強學習的信心.

總之，引言課是實施數學文化教育的好時機，能較好培養學生的學科素養.