清末民國時期歐美中小學數學教科書的中國化①

王 敏

(內蒙古師范大學科學技術史研究院 010022)

1 歐美中小學數學教科書傳入的途徑

歐美中小學數學教科書在中國的譯介大致可以分為兩種，一種是通過日本，一種是在中國直接翻譯或者編譯.清末，隨著中國向西方學習的浪潮，起初沒有更好方法的時候，先選擇通過學習日本而學習歐美的數學教育，中國接受的是經過日本加工的成品，夾雜了許多日本數學教育的內容.其中典型的例子，當屬通過周達及周新算社翻譯上野清及東京數學院引介歐美數學教科書，其中包括代數、幾何和三角.據何兆武先生的回憶：“有個叫上野清的日本人把這兩本書(范式大代數和Hall與Knight合編的代數)綜合起來，寫了一本完整的教科書，叫作《大代數學講義》，匯集了前兩本書的優點，而且編得很系統，所以這本書在當時的中學里邊非常流行，凡是數學拔尖的同學都讀，叫作‘開小灶’.”[1]85

上野清的眾多數學教科書均是集歐美眾家之言，其在《幾何學講義》的序言中提道：“予于編撰此講義錄之始.先歸集平日之草稿，札記，考試紙，質題等.又取英美德法幾何學書十種.并幾何學歷史.與之對.以定例題之次序、此乃解釋是等之例題.參考幾何學教改良協會所著幾何學書之順序.而設公理，定義，定理等.”上野清的數學教科書在中國的翻譯出版，不僅使中國教科書缺乏的局面得到了緩解，而且對于了解當時歐美著名數學教科書，如：赫爾、乃托氏的大代數學等有重要的意義.

新學制頒布之后，根據新的課程綱要，開始編輯新學制教科書.這一時期的數學教科書大多是在歐美數學教科書基礎上進行篩選、調整、重新組織到國人自編而成.隨著教科書審定工作的逐漸展開，數學教科書的編寫工作不僅要符合課程綱要的要求，還要適應數學教學的實施，當然這些工作是逐漸完成的.民國時期的數學教科書建設經歷了不斷完善和不斷進步的過程，在這一過程中，不僅實現了編排形式的轉變，而且完成了數學教科書內容的革新.

2 歐美中小學數學教科書中國化的過程

2.1 直接翻譯但內容與課程綱要規定不一致

清末民國時期，國內由于缺乏合適的數學教科書，不得不翻譯歐美的一些數學教科書以應當時教學之需，清末在正式學校系統實行之前，翻譯的數學教科書均屬于直接翻譯而且沒有任何改動.民國成立后，新的學校系統綱要中逐漸形成了較為系統的教學計劃，教學計劃的實施需要一些配套的數學教科書，但是這一時期仍有一些與教學計劃內容不符的數學教科書出現.另外，考察20世紀30年代的大學入學考試題目，集中表現為試題分量重、難度大，為了應付高考，各個中學數學教學不得不加入課程綱要以外的內容，使得涵蓋內容廣、難度較大、練習題較多的數學教科書仍然十分受歡迎.以下選取葛氏平面三角學在中國翻譯的情況進行說明.

民國時期在各個學校使用的平面三角學教科書，包括從開始使用英文原版三角學教科書，到使用翻譯和編譯版三角學教科書.初期使用的是溫德華氏、史密斯及龍氏等所著的三角學教科書，后期采用最多的是葛蘭威爾著的三角學教科書.1933年葛氏三角學教科書有莊子信、李修睦，褚保熙，高佩玉等以及王紹顏的譯本，這四個譯本均為直接翻譯葛氏平面三角學教科書(如圖1).然而1932年教育部頒布的《高級中學算學課程標準》教材大綱規定“三角學部分”包括：(1)廣義之三角函數，基本關系式，三角函數變跡(圖解).(2)和角公式，化和為積法，三角恒等式.(3)任意三角形性質.(4)任意三角形解法，對數，測量及航海方面之應用問題.(5)反三角函數，三角方程.(6)三角函數造表法，表之精確度.通過比較以上四個譯本的內容及三角學教學計劃中規定的內容，發現其中內容(6)在原本及譯本中都沒有涉及，這四個譯本都是直接翻譯但沒有考慮課程標準中教學計劃的安排.

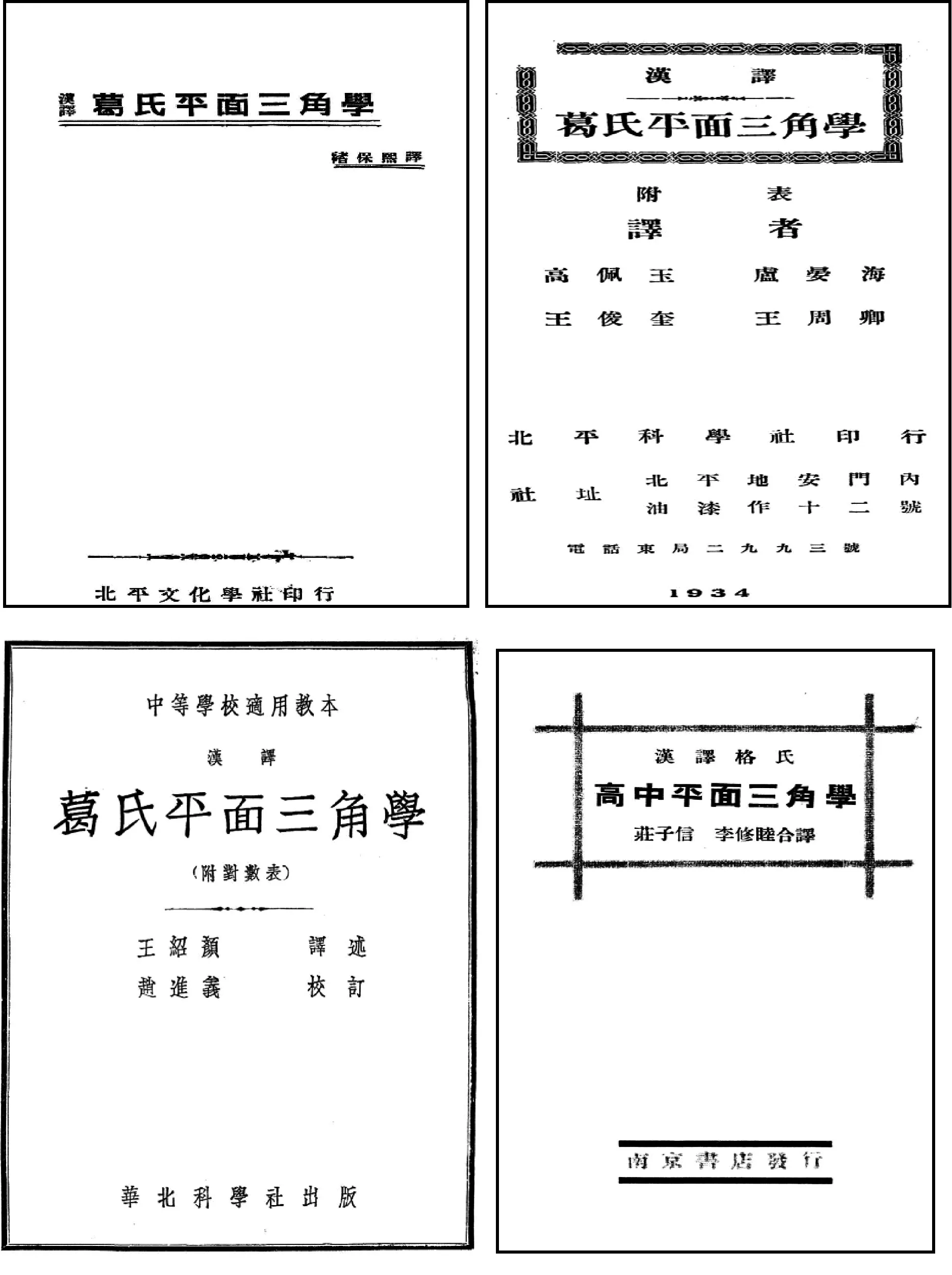
圖1

這樣的翻譯現象在溫德華氏數學教科書中體現的更加明顯，溫德華氏系列教科書在清末就被翻譯出版，新學制頒布實施之后，溫德華氏系列教科書的內容并不符合課程綱要的要求，但是溫德華氏系列教科書一直到新中國成立不斷有譯本出現.

2.2 根據課程綱要的內容，對原本直接翻譯

教育部對于數學課程實施給出了具體的實施步驟，集中反映在頒布實施的課程標準中，其中對數學課程綱要內容及時間的分配等都有明確的規定.在數學教學中采用的數學教科書的內容都要遵守相關的規定，按照標準中的原則進行編寫.新的課程標準的頒布與實施，促進了大量相應的數學教科書的出版，對于外文原版教科書中內容與課程綱要中規定的內容一致的數學教科書被翻譯使用.

1923年《新學制課程標準綱要》高級中學第二組必修的高中代數課程綱要中列出了代數科主要參考書[2]217，有Herbert.E.Hawkes著 Higher Algebra以及Fine；Charles Smith；Hall、Knight；Wentworth 分別編著的College Algebra.于是這些代數學教科書在新學制公布之后出現了許多相應的譯本，如李士奇翻譯的Herbert.E.Hawkes著《高等代數學》(Higher Algebra).Fine的代數學教科書更是有眾多譯本，如高佩玉譯的《漢譯范式大代數學》(北平科學社，1934)；沈璇等譯《漢譯范氏高等代數學》(新亞書店，1935)；駱師曾等譯《范氏大代數》(世界書局，1940)；鄭宗元譯《新譯范氏大代數》(復益書社，1949).Wentworth系列教科書也有許多的譯本，其中包括G.A.Wentworth及其兒子G.Wentworth與D.E.Smith修訂G.A.Wentworth的數學教科書.

黃彭年與江譚翻譯的《斯蓋尼三氏新解析幾何學》也是直接翻譯原版，斯蓋尼三氏的解析幾何學教科書與1932年頒布的《高級中學算學課程標準》中教學大綱規定的內容相符合，所以作者就直接進行翻譯，在譯者序言中提到：“譯者鑒于原書在我國通行之廣，而又適合于高中課程標準，際此提倡漢文教課之會，謹以語體譯為漢文，其不通英文者，固可資以討論，而英文程度較差者，尤可資為臂助也.”[3]序言這樣編譯的數學教科書很多，如裘友石編的《高中新平面幾何》(1937)就是依據3S《平面幾何學》一書翻譯的，且與當時實施的平面幾何課程綱要一致.

2.3 根據課程綱要的內容，編譯自多家數學教科書

隨著歐美數學教科書的大量翻譯，中國數學教科書市場出現了各家各派不同的數學教科書，教科書市場的繁榮，使得教師在選擇教科書時就出現了迷茫，到底該選擇哪些數學教科書進行教學也成為當時重要的研究課題.《中華教育界》在第19卷第4期出版了“教科書專號”，其中就中學數學教科書的情況分科進行了研究討論.另外《江蘇教育》在第3卷第7期也出版了“算學教學專號”，介紹了算學教學中教科書的問題，其中就直接翻譯歐美數學教科書中存在的問題進行了分析，提出歐美數學教科書對于中國學生不適宜以及不符合課程綱要的要求等問題，加之本身一些譯本存在的問題：如商務印書館出版的《漢譯溫氏高中幾何》教科書第204頁第2行及224頁第10行的錯別字，經過再版十余次仍沒有改正.南京書店出版的霍克氏《高中代數學》第171頁的17題完全錯誤，幾次經校者校對都沒有察覺.[4]70這些問題的出現以及一些譯本在教學中逐漸表現的不適宜，使得許多專家學者開始糅合眾家之言改編數學教科書.

秦汾編《民國新教科書三角學》(1913)編輯時參考書籍，為Todhunter，Hobson，Casey，Locke，Hall and Knight，Loney，Wentworth，Granville之作.習題亦多選于是.張敬熙著《解析幾何》在例言中寫道：“根據新學制課程標準起草委員會所擬定之新學制課程標準綱要編輯而起，……本書對Smith和Gale的《解析幾何原理》取材較多，他如Charles Smith之《圓錐曲線學》及Wentworth，Buwser,Lambert,Dowing and Turncaure之《解析幾何》亦隨時采入.”[5]例言馬純德著《初等代數學》是根據教育部新頒初中課程標準制成；以供給現今科學上所必須之普通代數知識，并以完成初等數學教育為目的.……本書教材參考書中西文初等代數書籍，不下二十余種.[6]廣告頁

薛天遨也針對教學過程中中文數學教科書缺乏，在不得不仰仗外文教科書時，根據教育部最近頒布高中代數學課程標準，并參考下列各書：①Fine:College Algebra；②Hall and Knight:Higher Algebra；③Hawkes:Higher Algebra；④Caro Bourlet:Lecons d’Algebra elementaire；⑤B.Niewenglowski:Cours d’Algebra；⑥何魯等著初等代數奇數變跡，編輯而成《薛氏高中代數學》教科書，并對其中的內容進行說明，就當時高中教科書中不夠完備的知識進行了補充，如變數，函數，極限，坐標，圖解等，為代數學之基本知識，故在基本四則以前，將其列舉而討論之.方程式解法的討論，函數的變跡，是現代高中教科書中最缺乏的教材，本書對于此種教材，特別豐富.[7]編輯大意

在《中等算學月刊》中刊登的教科書發行廣告中介紹了余介石的兩本數學教科書的發行，其中寫道：“本書(指余介石的《高中三角學》中華書局，1934)參考英法日各國三角學十余種并依據部頒課程標準及江蘇省高中算學進度表編成，曾在南京各中等學校試用多次結果極佳，全書以角函數三角形三種基本觀念為中心，分為單元編制材料豐富而有彈性理論精當而甚明晰誠，為刻下高中最適宜之優良課本也.”其編著的《高中代數學》(中華書局)適用于新課程標準，在編著過程中“曾參考中英法日書籍十余種融會諸說而獨成機杼教材排列之審慎理論之透徹應用之宏博蓋兼美國教本編制完善與歐洲教本理論精當二者之長”.[8]這兩種教科書是參考了十幾種代數和三角學教科書集合在一起編譯的.但是經過十幾年的時間后，余介石仍然參考其中的一些歐美包括中國翻譯的歐美數學教科書編譯教科書.

余介石著《新中國教科書高級中學三角學》(正中書局，1946)，在其“編輯大意”中指出：“本書取材，完全遵照教育部最近修正的高中課程新標準，高中一年級采用，最為相宜.美國人Granville所編平面三角學一書，在我國流行甚廣，本書即采用這書為藍本改編而成.……本書除以Granville原書為藍本，并參考下列各書：(1)Hobson：Plane Trigonometry；(2) Hall and Knight：Elementary Trigonometry；(3)Chauvenent：Plane Trigonometry；(4)Wentworth：Plane Trigonometry；(5)長澤龜之助：三角法辭典(薛德炯譯)；(6)余介石：新課程標準適用高中三角學(中華書局)；(7)何耔嶔：龍氏高級三角學；(8)倪德基：數學辭典.”[9] 編輯大意

2.4 對歐美數學教科書部分直接翻譯，部分改編

在對歐美數學教科書進行借鑒學習到自編的過程中，有一些數學教科書是采用部分直接翻譯，部分進行改編完成的.如馬文元編譯的Hall和Knight合著的Elementary Trigonmetry(《平面三角學》,戊辰學會編輯部，1932)在其編輯大意中寫道：“……前十四節完全照譯，兼有曾附.十五十六兩節刪去七位對數表之用法.十七節刪去不在同一平面上之問題.十八節刪去有法多邊形以次各段.十九節照譯.二十節只譯一部.二十一節以后，只遷譯極限值，消元法，解方程式法等另定節名.并增入聯立三角方程式一節.在原書所附對數表，函數表，習題答案之外又增入國立各大學三角法入學試題，以便學者自修兼測驗自己學業之用.”

2.5 借鑒歐美數學教科書的基礎上自編

民國后期，教育部明令必須使用中文教科書，這一時期，不僅使得一些外文原版數學教科書紛紛翻譯出版，而且中國學者開始自編數學教科書，并在以往直接翻譯、編譯歐美數學教科書的基礎上進行了一些有益的嘗試和改進.但是在這些自編的數學教科書中仍不乏有歐美數學教科書的影子.許多專家學者包括數學教師在借鑒歐美數學教科書的基礎上，結合中國數學教育實際及數學教學中存在的問題，在借鑒以往數學教科書的基礎上進行自編.

1932年教育部頒布的《高級中學算學課程標準》中教材大綱中規定“三角學部分”中(6)三角函數造表法，表之精確度.在Granville著的平面三角法一書中沒有相關內容，所以韓桂叢等在翻譯時，增加了這部分內容，在編輯大意中指出：“原著所列教材，均與教育部新頒課程標準相符，惟三角函數之造表法及其精確度略論一項，尚付闕如，本書特增入一章，以謀適合.”[10]編輯大意比較韓桂叢與褚保熙等對于葛氏三角學的不同譯本，就會發現，韓桂叢的譯本(如圖2)在最后加了“第十章 三角函數表之造法及其精確度略論”一節，而其他幾個譯本均沒有.

圖2

民國時期自編數學教科書的編寫者不僅有數學教育專家，還有一些是數學教師，他們對于哪些教科書更有利于學生學習以及數學教科書在教學中存在的問題等都很熟悉，組織這些教師編寫的數學教科書更有利于當時數學教科書建設.于是1930年上海開明書店集合了眾多數學教師進行編寫數學教科書，如周為群、劉薰宇、章克標、仲光然參考國內外三角學教科書編輯而成的《開明算學教本·三角》.

民國時期自編教科書的教育研究者中余介石的工作是值得注意的.余介石，安徽顆縣人，畢業于國立東南大學，獲理學學士學位.曾加入中等算學研究會、兼聲編譯合作社等團體.曾任東南大學、中央大學講師，國立編譯館編審，重慶大學教授.他編譯編寫了很多中學數學教科書和數學參考書，僅由商務印書館、中華書局、南京書店、中等算學研究會、國立編譯館、上海北新書局就有三十余種.

余介石在對歐美數學教科書的借鑒基礎之上，總結其中的優點及不足，進行改編，另外還結合中國的課程標準要求進行自編教科書.在此過程中，余介石深入分析歐美數學教科書的特點以供編輯數學教科書的工作者服務，如余介石總結的《葛氏平面三角學》教科書的優點及缺點，以供譯者在翻譯過程中借鑒.

縱觀余介石1934年到1946年編寫的三角學教科書，雖然參考了Granville的平面三角學教科書但對于其中的缺點進行了改進，對其中的優點進行了補充.如1934在《高中三角學》一書中針對原來Granville原書中沒有論及三角函數造表法及表的準確度的內容，余介石遵照課程標準的要求，在這一內容上選取了辛普孫(Simpson)的方法，因為三角函數造表法，原以用無窮連級數計算為便，但無窮連級數的斂散性，須學過高等代數的方可明了，又展三角函數為連級數的方法，不但高一學生不易了解，且須先講過二項式定理與棣美佛(De Moivre)定理，涉及問題太多.而且高一學習造表法的目標，不過是略示表的由來，并非要學生去自行造表，就這一方面看來，選擇辛普孫(Simpson)的方法最為適宜.[11]編輯要旨

另外，余介石對于中學數學教科書編寫工作進行了理論上的探討，強調“欲求完善教本，須出版家、編者及教師三方面通力合作不可”.在教科書編撰完成后，余介石建議“撰成的教材，在多數學校內試用，再經過致密詳盡的討論，始為最后的決定.”[12]16并在此基礎上他給出了教科書編撰原則.

3 歐美中小學數學教科書中國化的特點

3.1 翻譯的主要原因是學生對于英文教科書學習的困難

在數學教科書翻譯方面，翻譯的主要原因是國內中學數學教育缺少中文的數學教科書.當時的學習者不僅是學校的中學生，有些是沒有英文基礎自學的學生，另外在教學過程中發現：“中學生英文程度參差不齊，內地尤甚，大半時間均消磨在翻閱字典，推敲文句，以致主要部分之演習，反感時間不足，草率了事”等現象.于是，教科書編寫者甚至一些數學教師開始翻譯歐美的數學教科書以應之需.同時還為了便于對照學習加強理解而翻譯，如“漢譯溫德華氏數學教科書”為了“使不能讀原書者，有捷徑以探其奧.已曾讀原書者.可對照而會其通云爾.”[13]序言

3.2 當時的數學教科書針對不同的學習群體

新學制實施后規定了分學段的學制系統，小學教育分為初級小學和高級小學，中學教育也分為初級中學和高級中學，同時還有與之平行的師范學校和職業學校.初級中學施行普通教育，還應地方的需要，兼設各種職業科.高級中學施行分普通、農、工、商和師范等科，各地方還設立了中等課程的補習學校或補習科.[14]84不同學校的設置在教科書的編寫上就存在一定的困難，不僅在內容上要符合不同學校的教學要求，而且在教學材料的選擇上要為學生以后從事的職業考慮.

葛蘭威爾(W.A.Granville)在其著作中指出該書是為專門學校、實業學校、師范學校、高級中學及自修的學生編寫的，所以編者對于教師在教學中留有酌減的余地，以適合不同學生的使用.張敬熙著的《解析幾何》適用于大學預科及高級中學使用.這些在不同編寫目的下編著的數學教科書，從某一個視角分析會發現一些問題，但由于當時教科書的缺乏及教科書編寫的困難，這些都是不可避免的.

3.3 數學教科書的使用具有一定的彈性

針對當時數學教科書存在不因地制宜的現象，許多數學教科書在直接翻譯或編譯的過程中對于內容的選擇留有很大的余地，不僅是因為數學教科書使用的對象不同，而且因為歐美的高中生大多都要升學繼續深造，所以其數學教科書習題較多，涉及大學數學內容也多，而這一情況在中國是不適宜的，于是在翻譯與編譯的過程中，很多材料都是酌情處理.其中在教科書的“編輯緣起”或“編輯大意”中都有體現.

如莊子信與李修睦翻譯的《格氏高中平面三角》在編輯大意中強調：本書材料，對始讀三角學者，雖覺過多，然書中材料，已善為排定，教者可按其需要，加以裁剪也.在對余介石的《高中代數學》(中華書局)的介紹中也說明：“本書具有充分彈性材料留有絕大伸縮地位故能合高中普通科示范科職業科之用”.

另外，高中數學教科書在內容選擇和順序的調整方面也具有很大的伸縮性，主要原因是學生從初中升入高中時學習水平不一致，在學習材料的選擇和教學順序上也有彈性，如余介石編著的《高中三角學》一書，如果學生在初中就沒有學習過數值三角，那么高中一年級就應該詳細講解該書第一章，而對于書中帶有星號的章節可以選擇不學，這樣有“五分之一的教材可以酌量省略”，而且帶星號的部分屬于課程標準要求以外的知識，屬于補充知識，這些可以讓班級中成績優良學生自學.[15]編輯要旨

除了在數學教科書的編輯中，許多數學教育研究者也提出，要對歐美數學教科書進行一些處理，用英文原版的翻譯中，應將不合國情的部分，一律刪去，而補充日常應用的知識.另外，中國幅員遼闊各地學生程度不一，甚至一個班級的學生能力也是參差不齊的，所以在教學中對教學內容做適當的重新組織.所以該時期的教科書在使用上的調整余地很大，伸縮性強.

3.4 翻譯的教科書在歐美屬于陳舊教材已不使用

中國直接使用或翻譯使用的歐美數學教科書一方面是通過日本引進，另一方面是通過留學生歸國帶回.日本在明治維新后期學習歐美的數學教育是歐美傳統的舊的數學教育，然后傳入中國，中國在翻譯歐美數學教科書方面屬于落后的狀態，如溫德華氏數學教科書在美國20世紀20年代就沒有再出版過，可在中國20世紀后半葉仍有翻譯使用的情況.這些情況在民國時期已經被一些學者認識到：Hamblin-Smith一流之書，以時代思潮論之，已遠在十八世紀之末；Wentworth之書，仿佛十九世紀初葉之風，Wentworth-Smith之書，小處有進步，大處無足取.[16]卷首可見中國在歐美數學教科書選擇上是不先進的.

3.5 教科書中加入數學思想方法及數學教學法要求

隨著新學制的制定，受實用主義教育思想的影響，在數學教學材料的選擇方面強調與實際生活的聯系，在教學過程中關注學生的個性發展，這些內容在數學教科書中也有明顯的呈現.

美國在19世紀出版的教科書中不僅包含教學內容還包含教學法，而且對學習者還有一些建議.如，1801年美國的Daniel Adams出版的《算術教科書》[17]，該教科書的大量出版使得它成為1800-1825年美國第二大暢銷的算術教科書，其中包含“規則教學法”即通過演繹的方法確定一些法則，然后運用它們.書中還對學習者提出建議：如鼓勵初學者在學習中犯一些錯誤，但經過反復的練習就會好一些等等.另外，該時期的美國數學教科書將一些教育家的理念融合其中，形成獨特的編寫理念和教學方法.如1821年，反映裴斯泰洛奇哲學體系的第一本數學教科書在北美地區出版，即Colbum著的《Arithmetic on the Plan of Pestalozzi; with some Improvement》，該書對數學教育的影響很大，書中的教學法采用了歸納法，表現為數學教師應該幫助學生舍棄死記硬背和機械方法解決問題，幫助學生發現所包含的基本原理.

這些教科書編寫理論在中國20世紀以后經過眾多次教育改革并吸收借鑒歐美的教科書之后，在數學教科書中也有所體現.以下列其中幾例說明.

1930年，胡雪松和龔昂雲編著的《初中三角》，在編輯大意中強調該書在編著過程中注重理論知識與實際應用的結合，并在問題的選擇上關注學生的學習興趣，具體內容如下：“取材簡單而于理論應用，同樣注重.……故應用方面，須有解決的能力；而理論方面，亦須有充實的基礎，本書選材，即為本旨.……本書體例謹嚴，說理精賅，舉例亦詳，選擇問題，多能引起興趣者為主.”[18]編輯大意1923年劉正經編著的《三角術》現代初中教科書，在編排方面加入了關于三角學歷史上的談話——關于中國和外國兩個方面，主要是要使得學生了解三角學的歷史沿革，并且引起學生的興趣.

在中華書局的廣告中宣傳的新學制適用《新中學教科書》中對每一科都標明了其中相關數學教育理念的滲透.如①算術：吳在淵、胡敦復編中強調：“習算以明理為先本書注重理法于異同順逆等皆詳細比較反復說明并載各種特別算法以便應用.”②代數學：秦汾、張鵬飛編中強調：“根據算術以說明代數學之理法而于代數學數之性質初學不易明了者解說尤詳明并注重函數圖表以為進而學習高等數學及其他應用上之預備.”③幾何學：胡敦復、吳在淵編中強調：“本書將平面立體混為一凡屬相關之理莫不聯絡比較闡發盡致在幾何學中別開生面.”④平面三角法：胡仁源、張鵬飛編中強調：“全書分量不多能夠以極經濟之時間而得平面三角之重要學識，但于公式及求法之說明不憚多舉解證養成圓滿之推理力.”

4 小結

縱觀清末民國時期數學教科書的發展，歐美數學教科書在其中起了重要的作用，期間經過直接翻譯使用到編譯再到自主編寫的過程，并呈現了不同的特點.這些數學教科書培育了一批著名的數學家、科學家，其貢獻是不容忽視的，他們作為接受歐美數學教育的一代，還經歷了中國傳統經典的熏陶，這樣的結合使得他們的地位處于兩種世界的中間，最終有著不一樣的成就.