城市需水量預測方法與模型綜述

董云程 周明 杜坤 盧慢 黃樂烽 楊佳莉

摘要：通過需水量預測能實現城市供水系統(tǒng)最優(yōu)控制，以達成供需平衡和節(jié)約能耗目的。分析2010-2019年部分有關城市需水量預測相關文獻，對現有城市需水量預測方法與模型進行綜述，提出目前需水量預測存在的問題及建議，為城市需水量預測后續(xù)研究提供基礎與借鑒。

關鍵詞：需水量預測;時間序列;供水系統(tǒng)決策

DOI：10.11907/rjdk.192178

文獻標識碼：A 中圖分類號：TP306

文章編號：1672-7800（2019）012-0001-05

0引言

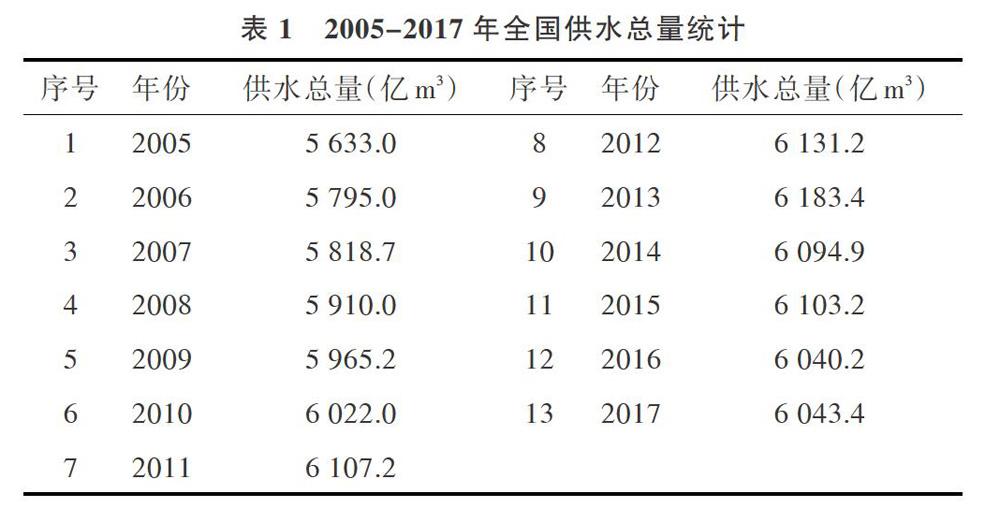
城市需水量預測能為供水單位運行和決策提供科學依據，城市供水單位需掌握今天和明天的需水量數據，從而恰到好處地運行供水系統(tǒng)以滿足客戶用水需求。呂謀等研究表明，對供水系統(tǒng)調度運行費用采用時用水量預測結果進行優(yōu)化，以電費為評價指標，將此方法與常規(guī)經驗調度方式相比較，能夠節(jié)約3%～5%的能源開支。近年來，大力推進的城市化進程和高速發(fā)展的社會經濟，均導致了城市用水量大幅度增加，因此供水單位的當務之急便是擴大城市供水系統(tǒng)規(guī)模以滿足客戶用水需求。根據2018年《中國統(tǒng)計年鑒》（見表1），全國供水總量呈上升趨勢。

現有預測方法與模型能為需水量預測提供較大幫助，但其應用在供水單位的需水量預估也存在諸多問題，例如：現有數據的準確性、影響需水量預測的眾多變量、所涉及的預測范圍以及預測周期的多樣性均會影響需水量預測結果可靠性。李穎等對多種預測方法和模型進行了評價和優(yōu)選，其所提及的模型與方法均有不同的預測性能，盡管能夠找到合適的預測方法進行需水量預測，但在全面預測上需作進一步研究;聶紅梅等將主成分回歸法、逐步回歸法、灰色模型以及BP神經網絡4個模型在城市需水量方面進行比較，上述模型的局限性可能導致信息缺乏完整性、預測結果不準確。城市供水單位還需要預測未來20-30年的需水量，為開發(fā)新的水源或擴大其供水系統(tǒng)規(guī)模決策提供可靠數據支持。城市需水量預測方法和模型需要不斷完善，尋求高精度的城市需水量預測方法和模型是大勢所趨。

本文對2010-2019年需水量預測相關文獻進行綜述，可為城市需水量預測研究提供借鑒，為供水系統(tǒng)決策和管理提供相應方法和模型參考。對于研究人員而言，目前他們尋求擴展該領域內最先進的預測技術。為此，本文介紹需水量預測框架，根據供水單位規(guī)劃水平、預測范圍和預測周期對產生需求的用水決策問題進行描述，從而為需水量預測奠定基礎;對部分預測方法和模型進行綜述、歸納和整理，總結其優(yōu)勢與不足;最后提出目前城市需水量預測中存在的問題，并給出解決此類問題的建議。

1需水量預測框架

1.1需水量預測依據

需水量預測作為其供水單位決策規(guī)劃的基礎，能夠為決策規(guī)劃所涉及的供水系統(tǒng)運行、管理和優(yōu)化提供先決條件。在規(guī)劃和運行供水系統(tǒng)時，供水單位的目的是滿足客戶用水量需求，這意味著在合理壓力下，不斷向用戶提供足夠數量的優(yōu)質水，從而確保供水系統(tǒng)具有良好的可靠性與穩(wěn)定性。城市需水量預測可分為長期預測、中期預測、短期預測3種時間尺度上的預測。長期預測主要用于規(guī)劃和設計層面，而中、短期預測在操作和管理方面有用，并有助于自來水公司管理人員在平衡供水需求時，能夠更明智地作出有關供水管理方面的決策。劉裕輝等研究表明，城市需水量科學、準確的預測結果能夠為城市供需水量平衡決策提供合理依據。以天津市濱海新區(qū)2020年需水量預測為例，預測結果均屬于合理范圍內，并為此區(qū)域供水系統(tǒng)發(fā)展規(guī)劃提供了主要依據。本文總結了供水單位規(guī)劃層次、決策問題與預測屬性之間的關系，如表2所示。

1.2需水量預測變量與決定因素

在城市用水中，許多預測變量被認為是影響城市需水量的因素，這些變量從社會經濟到天氣相關變量的各種衍生變量不等。周晨等將東北地區(qū)的水庫蓄水總量、人均可支配收入、綠地面積以及工業(yè)用水量等作為5個因素并對東北地區(qū)需水量進行分析;Shine等分析了奶業(yè)生產、庫存數量、基礎設施設備、管理程序和環(huán)境條件等6個因素對奶牛場用電量和用水量的影響。眾多需水量決定因素（外生變量）是增加需水量預測復雜性的主要特征。

1.3預測誤差度量

將預測結果與觀測結果進行比較最終得出預測精度，然而預測誤差可作為一種衡量預測精度高低的方式，因此為了保證預測結果具有較高的預測精度，預測誤差選擇尤為重要。例如：平均絕對誤差（Mean Absolute Deviationma，MAD）將所有預測誤差取絕對值后計算的平均誤差;均方誤差（Mean Square Error，MSE）利用平方將誤差的正負號消除后所計算出的平均誤差;平均百分比誤差（Mean Percent-age Error，MPE）和平均絕對百分比誤差（Mean Absolute Per-centage Error，MAPE）二者能作為反映誤差大小的相對值，一定程度上消除時間序列數據水平和計量單位影響。其預測誤差的選擇取決于預測者的最終預測目標與對所采用預測方法的熟悉程度。

2需水量預測方法與模型綜述

現有需水量預測方法有傳統(tǒng)預測（回歸分析、時間序列分析、指數平滑等方法）和新型預測（人工神經網絡、混沌理論、機器學習、復合模型等方法），傳統(tǒng)和新型預測方法皆為需水量預測領域提供了較大幫助。本文對2010-2019年期間出版的需水量預測文獻中所提及的傳統(tǒng)和新型需水量預測方法及模型進行分析、歸納、整理和綜述，并分析城市需水量預測方法和模型發(fā)展及研究趨勢，為未來尋求新的研究突破提供借鑒。

2.1傳統(tǒng)預測方法

需水量預測是一個非常活躍的研究領域，早期主要使用傳統(tǒng)預測方法進行需水量預測工作。傳統(tǒng)預測方法的先驅是統(tǒng)計學理論，主要包括回歸分析法、指數平滑法、趨勢外推法、移動平均法等。對于城市供水系統(tǒng)而言，其具有較強的周期性和隨機性，因此，使用傳統(tǒng)預測方法進行城市需水量預測時，為了取得理想效果，應根據序列性質進行合理假設。本文對應用較為廣泛、預測效果良好的回歸分析法和整合移動平均自回歸模型進行綜述。

2.1.1回歸分析法

將回歸分析應用于城市需水量預測，通過尋找需水量與影響需水量因素之間的因果關系，從而建立回歸模型進行預測。根據這些關系，可以采用線性回歸、邏輯回歸和多項式回歸等多種方法，其中一元回歸分析只涉及單個變量，多元分析則涉及多個變量。回歸分析可根據回歸方程的表達形式分為線性回歸和非線性回歸，非線性回歸可以通過變量變換，將非線性回歸變?yōu)榫€性回歸，而利用線性回歸方法時，其回歸系數值需要運用最小二乘法原理求出，從而得到預測模型。

Yasar等對土耳其亞達納城建立了供水量與其它眾多因素（平均水費、總人口數、大氣溫度、氣壓、降雨量等）的多元非線性回歸模型，并通過多步預測，最終得出最符合該城的需水量預測模型。

金東梅等基于多元線性回歸模型對長春市2020年需水量進行預測，同時采用2013-2016年需水量數據檢驗模型適用性。結果表明，該模型擬合情況良好，能為長春市2020年水資源發(fā)展規(guī)劃提供數據支撐。

李孝朋等在礦井涌水量預測中采用了多元回歸分析法，結果表明，預測的相對誤差在允許誤差范圍內，并且此方法使用簡便，有利于相關煤礦工作人員根據當地實際情況對礦井的防治水進行分析。

Polebitski等利用3種回歸模型基于12個月的需水量預測，解釋了美國普吉特海峽地區(qū)、西雅圖和華盛頓等區(qū)域內住宅需水量與其供水基礎設施擴建、水資源管理等決定性因素之間的關系。

本方法計算方便簡潔，若在供水系統(tǒng)沒有發(fā)生重大變化且數據波動較小的年用水量預測上采用本方法則會取得良好效果。因而，在使用回歸分析法時，對自變量的選擇以及歷史數據的準確性皆有較高要求，若在影響因素復雜且數據波動較大的城市需水量預測上采用此方法則達不到良好預測效果，例如城市時需水量預測。影響需水量因素的選取、原始數據的準確性以及選用模型的適用性都對該方法起著決定性作用，在選用此方法時應當著重注意上述3方面問題。

2.1.2整合移動平均自回歸模型

整合移動平均自回歸（ARIMA，即Autoregressive Inte-grated Moving Average）是自回歸和滑動平均模型的綜合。此模型由Box & Jenkins于70年代初提出，ARIMA模型起源于自回歸模型（AutoRegressive，AR、移動平均模型（Mov-ing average，MA）以及自回歸滑動平均模型（Auto Regres-sion Moving Average）。模型通常表示為ARIMA（p，d，q）和包括自回歸（AR）、整合（I）及移動平均（MA）分別記為自回歸項p，移動平均項q，和差分次數d。其中心思想是運用數學模型近似描述一個隨機數列（此序列為時間序列），ARIMA模型的應用步驟主要包括模型識別、參數估計、診斷檢查和預測。

張吉英等基于ARIMA模型對沈陽市月降水量進行分析，根據沈陽市2005-2016年降雨量特征，建立了ARI-MA（1，1，1）預測模型，通過對模型的診斷和驗證，對2017年1-12月份沈陽市降雨量進行預測。盡管沈陽市月降水量年內及年際變化較大，但結果表明，該模型可以準確地對沈陽市降雨量進行預測分析。

Paulo等采用雙季節(jié)性ARIMA模型對某地區(qū)進行為期一天的需水量預測。僅利用歷史需水量數據作為解釋變量，并將和聲搜索法應用于ARIMA模型的參數估計（和聲搜索優(yōu)化算法是基于音樂理論過程搜索完美和聲的方法）。結果表明，通過實測的居民水表讀數與ARI-MA模型生成的時間序列進行比較，吻合程度較好，因此驗證了該方法的有效性，為未來一天的需水量預測提供了高精度模型。

趙凌等通過建立ARIMA的乘積季節(jié)模型，用于對成都市2010年全年月需水量進行預測，用2006-2010年2月供水量數據作為基礎數據，并對最后的殘差進行分析。結果表明，該模型具有良好的擬合效果，能夠提取有效信息以及更好地預測需水量。

若在時間序列為線性非平穩(wěn)時間序列，且時間序列內沒有數據丟失的情況下，使用ARIMA模型擬合時間序列進行預測，能取得較好的結果。ARIMA模型原理簡單，具有預測結果精度相對較高并兼具收斂快和魯棒性強等優(yōu)點，但是ARIMA是基于線性數據的模型，如果在非線性數據上進行序列分析，則會導致模型在非線性序列上的預測精度降低，得不到理想的預測效果。因此，該模型較宜使用在時需水量、日需水量、月需水量和季度需水量預測方面，一般不用于年需水量預測（大部分年需水量數據具有較強的非線性特點）。

2.2新型預測方法

傳統(tǒng)預測方法的不足之處是易受眾多因素影響，對歷史數據的準確性要求較高，大多數模型是基于全局角度而建立的，結構相對簡單容易導致最終預測精度偏低。為了提高預測精度，一些新的方法應運而生，目的在于尋找可靠的預測方法。新型預測方法包括機器學習、人工智能、混沌理論、專家系統(tǒng)等。據目前研究狀況，用于我國城市需水量預測最多的新型預測方法是灰色預測模型、人工神經網絡、機器學習以及其它組合模型等方法，本文著重對最常用的人工神經網絡以及組合模型進行綜述。

2.2.1人工神經網絡

人工神經網絡（Artificial Neural Networks，ANN）是基于模擬人類神經系統(tǒng)結構進行學習和處理問題的非線性系統(tǒng)。該模型由若干個神經元節(jié)點以及連接它們的權值構成，能夠實現輸入變量到輸出變量的非線性映射。神經元按層排列，每層之間的神經元通過稱為權重的鏈接連接在一起，通過對這些連接的調整，從而達到信息處理的目的。據近年來研究發(fā)現，運用于需水量預測的人工神經網絡模型屢見不鮮，其中最常見的有誤差反向傳播前向神經網絡（BP神經網絡），以及徑向基（RBF神經網絡）、廣義回歸神經網絡（GRNN）等。

Zhou等運用ANN模型模擬每周需水量的峰值需求，這些需求水平可以根據氣候變量（如氣溫、體積和降雨）和以前的需水量制定。研究表明，該模型具有良好的擬合效果和較理想的預測精度。

Bennett等采用3種傳統(tǒng)神經網絡：兩種前饋、反向傳播網絡和徑向基函數網絡，建立住宅用水用途需求預測模型。最后得出，人工神經網絡建模方法是建立住宅用水量最終利用預測模型的一種可行方法。

舒媛媛等將延安市1990-2010年需水量數據作為基礎數據，在基于主成分分析的BP神經網絡上對延安市2015年需水量進行預測。結果表明，預測值與實際值吻合度較高，該模型能夠適應需水量預測較強的非線性特點。

郭冠呈等預測常州市某供水管網DMAl5min的需水量時采用雙向長短時記憶循環(huán)神經網絡模型。結果顯示，該模型在傳統(tǒng)預測的基礎上提高了預測精度并改善了穩(wěn)定性，若在需水量波動較大的區(qū)域進行需水量預測，可以優(yōu)先考慮此模型。

人工神經網絡具有較強的記憶能力、非線性映射能力以及很強的學習能力等優(yōu)勢，但也存在一定缺陷，例如訓練時間長、局部極小、網絡結構難以確定等。據目前研究，由于大部分需水量時間序列具有時序性和非線性等特點，因此使用人工神經網絡進行需水量預測能夠得到較高的預測精度。

2.2.2組合模型

根據近年來研究發(fā)現，用于需水量預測的單一預測模型存在局限性，每個單一預測模型皆有優(yōu)勢與不足，與每個單一預測模型相適應的需水量預測要求也不盡相同，為了在需水量預測上達到更好效果，有關研究人員提出了組合模型。組合預測模型的基本思想是利用每個模型的特性在數據中捕獲不同的信息，再將不同的信息組合起來建立一種新的預測模型。理論研究和實踐都表明，將不同方法結合為一種方法能夠有效改善預測精度。

蔣白懿等運用一種灰色遺傳神經網絡的組合模型預測A市s區(qū)2014年年需水量。結果表明，組合模型相比單一模型精度提高了0.84個百分點，誤差也有所降低，該組合模型是一種有效的年需水量預測方式。

Brentan等運用混合回歸模型對城市時需水量進行預測，該模型建立在離線支持向量回歸模型的基礎上，構成預測基礎和在線自適應傅立葉級數預測偏差。研究表明，該模型的聯機功能有助于供水系統(tǒng)運作和管理，以節(jié)省能源和成本。

展金巖等運用組合模型進行某區(qū)域需水量預測，在此過程中，將組合模型對各預測模型進行整合優(yōu)化。最終得出，組合模型在需水量預測方面有著較好的預測精度和擬合度，較單一模型更全面科學，在區(qū)域需水量和水情災害評估上得到了廣泛運用。

據目前研究看，組合模型在一定程度上均表現出較單一模型更好的預測能力，尤其在解決復雜需水量預測問題上，組合模型有舉足輕重的作用。單一預測模型很難充分利用時間序列上所呈現出來的信息，組合模型能夠很好地解決此問題，但在運用組合模型進行需水量預測時，也要考慮到時間序列特性、模型相適應程度、模型操作性能等因素，這樣才能更好地發(fā)揮組合模型的積極作用。

2.2.3預測方法與總結

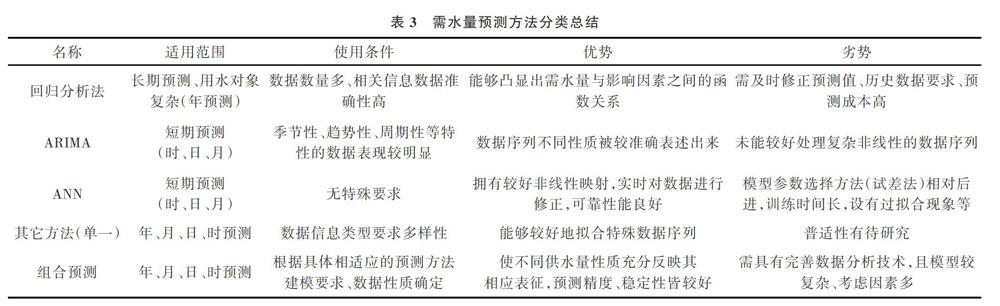
綜上所述，對各類城市需水量預測方法和模型進行分類總結，結果如表3所示。

3需水量預測存在的問題及建議

據目前研究看，大量成熟的城市需水量預測模型得以運用，但部分需水量模型存在一定的局限性。神經網絡等用于長期預測難以取得良好的預測效果，但在短期預測上效果理想。因此，如果供水單位要作出反映需水量短期預測的決策，則需要更多地關注神經網絡等方法。近年來，新形勢下的預測方法和模型對現有大部分成熟的需水量預測方法和模型作出了進一步優(yōu)化，例如：深度學習方法逐漸應用于需水量預測。牟天蔚等提出一種基于深度學習框架的小波深度信念網絡（SW-DBN）時間序列模型對城市日需水量進行預測，該模型比BP神經網絡更適應大樣本預測，在一定程度上提高了城市日用水量預測精度;張薇薇等基于長短時神經網絡對某地區(qū)需水量進行預測，對小時級別的預測具有很好預測精度，對眾多需水量影響因素能夠有效處理。基于深度學習以及長短時神經網絡等方法皆是當前研究熱點，未來需水量預測領域將會對更多的預測方法和模型進行研究，以滿足需水量預測的高精度要求。

4結語

可靠的城市需水量預測能夠使得供水系統(tǒng)在滿足市民用水需求的同時，最大程度地降低運行能耗，節(jié)約運行成本。在實際城市需水量預測中要考慮到預測方法和模型適應性、歷史數據特征以及相關影響因素。本文基于2010-2019年需水量預測相關文獻，對現有部分常用需水量方法與模型進行了綜述，可為未來提出更加完善的需水量預測方法和模型提供借鑒。