風力發電機組變槳距控制器的研究

呂 義，劉 漫，樊 姍，段永強，滕招波

(湖北民族大學信息工程學院，湖北 恩施 445000)

為了降低風輪負荷以延長其使用壽命，抑制風力發電機組輸出功率波動以降低對電網的不利影響，大中型風電機組通常在額定風速以上采用變槳距控制，即通過改變風輪槳葉槳距角，進而相應改變風能利用系數，使機組輸出功率保持穩定。但是，風力發電機組具有較大的轉動慣量和較嚴重的非線性，且自然風速變化范圍大，使得對變槳距系統控制困難。

由于風能的隨機性和突發性，因此風力發電機組變槳距的控制會受到一定的影響，為此通過對變槳距控制器的研究來實現對輸出功率的穩定控制。文獻[1]介紹了采用PID控制器控制變槳距來消除系統誤差提高輸出功率的穩定性。文獻[2]設計了模糊變槳距控制器使風力發電機組具有更好的動態性能從而降低輸出功率的波動。然而常規PID控制器和模糊控制器對變槳距的控制效果并不是很理想。

對此本文提出了一種模糊自適應PID的控制方法。通過反饋響應對PID參數進行在線整定達到最優化，很好地解決系統動態與靜態之間的矛盾。將模糊自適應PID控制器應用于風力發電機組變槳距系統中，基于Matlab/Simulink搭建額定功率為1 500 kW的風力發電機組模型進行仿真。結果表明模糊自適應PID變槳距控制器響應速度快、穩定性強、控制效果好。

1 變槳距風電機組控制原理

風力發電機組一般包括風輪、傳動系統、制動系統、發電系統、變槳距系統、控制系統以及偏航系統等，其各部分是相互關聯相互影響，風力發電機組整體結構如圖1。

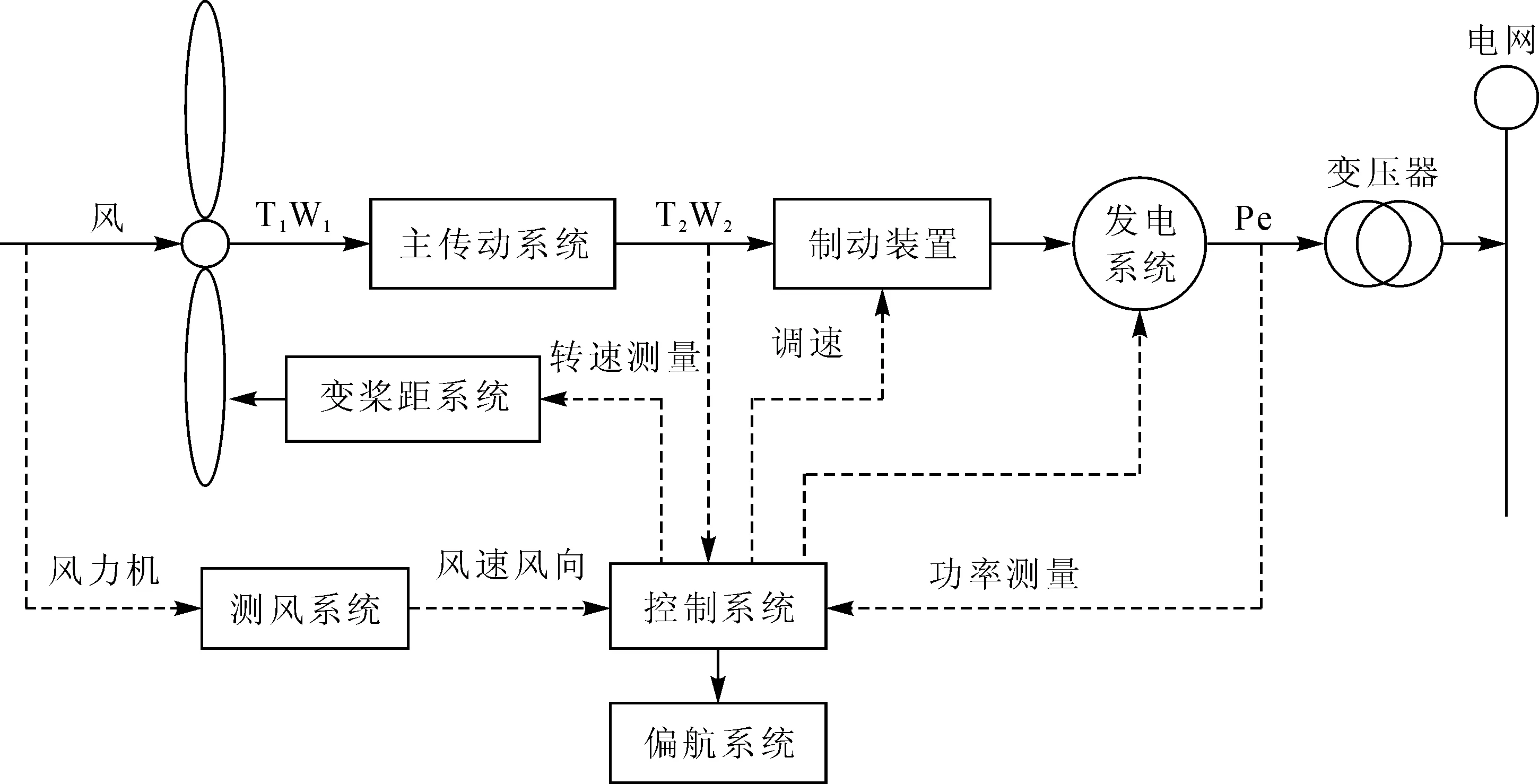
圖1 變速風力發電機機組結構

1.1 風輪模型

根據貝茲理論分析可知風力發電機吸收功率為

Pr=0.5ρπR3VW3Cp(β,λ)

(1)

而風輪獲得的氣動扭矩為

Tr=0.5ρπR3VW2CT(β,λ)

(2)

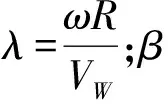
通過有關風能利用系數Cp是葉尖速比λ和槳距角β的函數：

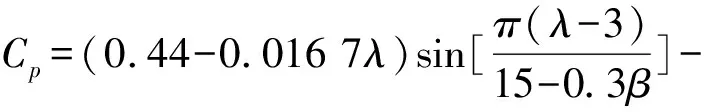
(3)

(4)

由近似函數可得圖2所示Cp的曲線。

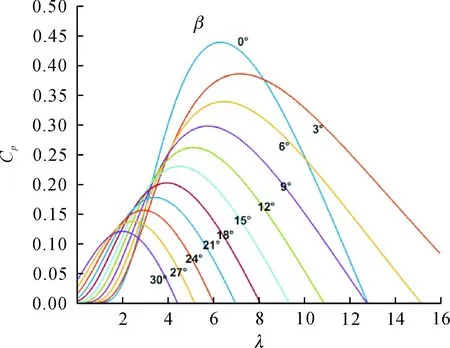
圖2 風能利用系數Cp曲線

根據圖2及公式計算得當槳距角的值取0°時，風能利用系數最大值等于0.593。而變槳距的目的是為了控制輸出功率，當風速低于額定風速時，則需控制發電機的反轉距來改變風輪轉速，從而實現低風速時在風速大范圍變化中最大風能捕獲，當風速高于額定風速的時候，因為風力發電機傳動是剛性軸此時發電機轉矩無法平衡風機的氣動轉矩所以改變葉尖速比并不能實現，只能通過調節槳距角的增加來降低風能的利用系數Cp，使風力發電系統的輸出功率保持額定功率的恒定狀態。

1.2 傳動系統的建模

傳動系統是在風輪和發電機之間，風力發電機組的傳動系統主要是由風輪轉子、低速軸、增速齒輪箱、高速軸和發電機轉子組成。忽略風輪和發電機部分的傳動阻尼，簡化傳動系統運動方程為

(5)

式中：Jr為風輪轉動慣量；n為傳動比；Jg為發電機轉動慣量；Tg為發電機的反轉矩；ω為發電機轉速，其中ωg=nω。

1.3 發電機的建模

風力發電機組中的發電機一般采用異步發電機，通過建立發電機的模型，發電機的反扭矩方程：

(6)

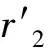
1.4 變槳距系統模型

目前風力發電機組的變槳執行機構通過發電機驅動來帶動槳葉的運行，其控制過程相當于激勵與響應的動態過程，可以簡化為一階數學模型：

(7)

公式(5)進行拉氏變換得：

(8)

式中：Tβ為變槳距執行機構時間常數，s；βr為參考槳距角，°；β為輸出槳距角，°。

變槳距執行機構模型如圖3所示。

圖3 變槳距執行機構結構

2 模糊自適應PID控制器的設計

2.1 模糊自適應PID控制方案

在風力發電機組中主要是控制槳距角，隨著風速不斷增大且超過額定風速的時，這時槳距角打開從而控制發電機的轉速變化直到發電機的功率因數達到最優值，最終達到穩定輸出功率的目的。而只有在超過額定風速風機才啟動變槳距控制，在風速小于額定風速變化到大于額定風速或從大于額定風速變化到小于額定風速時，只有當突變一定時間后，槳距角才會變化因此槳距角的調節具有一定延遲性。由于普通PID無法很好地控制時變性和非線性系統，一組整定好的PID參數遠遠不能滿足系統的要求，引入模糊自適應PID控制器通過反饋能在線整定PID參數，并利用模糊邏輯算法根據一定的模糊規則對PID控制的比例，積分，微分系數進行實時優化以達到較為理想的控制，其結構如圖4所示。

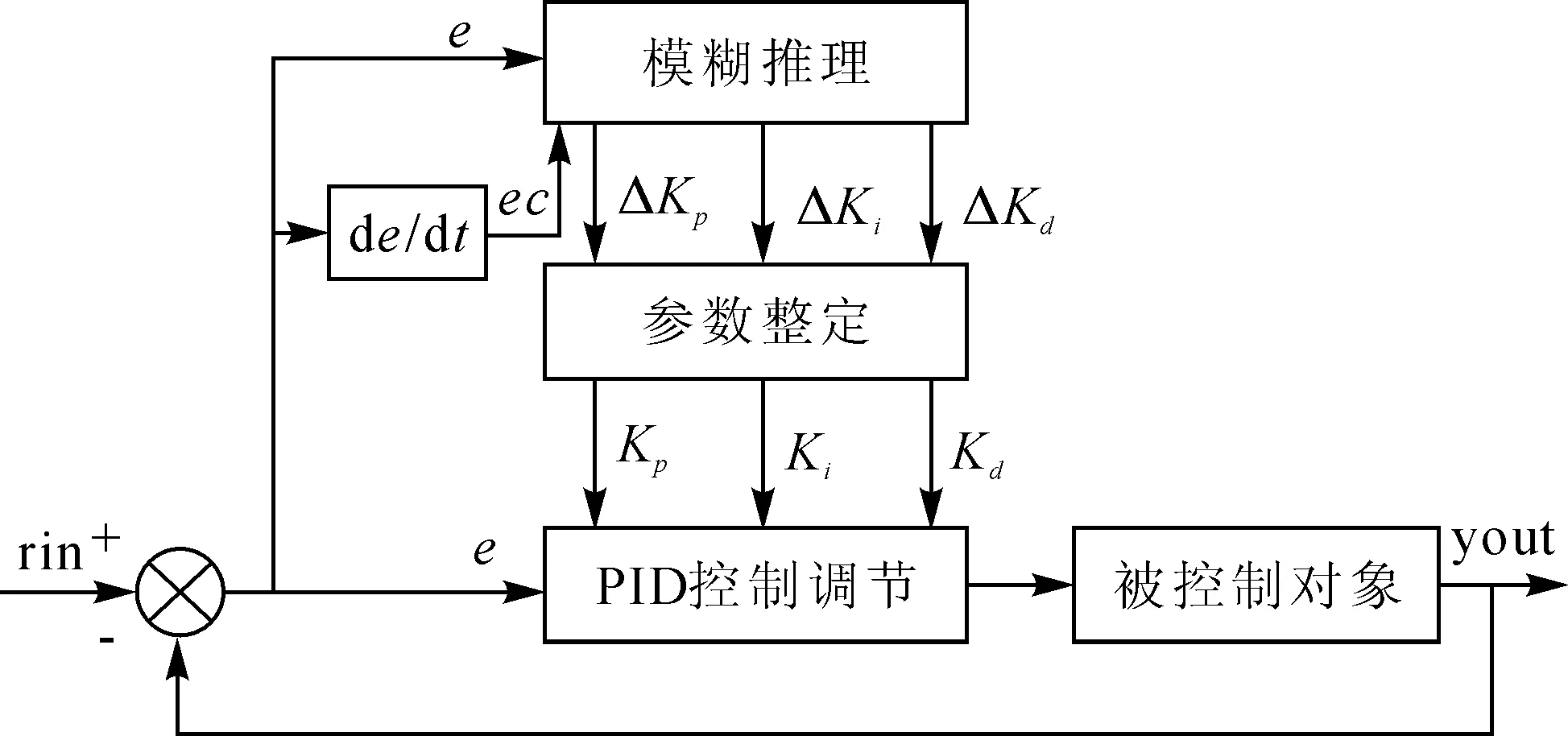
圖4 模糊自適應PID控制結構

模糊自適應PID控制器以輸出功率值與額定功率值的偏差e以及其偏差的變化率ec作為二維輸入變量[3-4]。把兩個變量輸入模糊自適應PID控制器，根據模糊規則來調節槳距角得到參考值，再與實際的槳距角比較，將槳距角誤差信號輸入到控制器進行控制。在系統運行的過程中不斷檢測e和ec，經模糊推理得到3個修改參數△Kp、△Ki、△Kd，將此修改參數和系統前一次的PID參數進行性線疊從而來滿足不同值的e和ec。

2.2 變槳距模糊自適應PID的設計

由于本文選用的風力發電機模型的輸出額定功率為1 500 kW，選擇輸入偏差e的允許范圍為[-400,400]，槳距角允許的最大速率變化是3°/s。選擇輸入的論域范圍為[-6,6]，輸出的論域范則圍都為[-1,1]，選擇的輸入變量偏差因子Ke=0.015，輸入偏差變化率因子Kec=0.5。在Simulink中設計模糊輸入隸屬度函數為高斯型輸出隸屬度函數則為三角型，e和ec輸入的隸屬函數是一致，而△Kp、△Ki、△Kd的輸出的隸屬度函數是一致。模糊子集[5-9][NB，NM，NS、ZO，PS，PM，PB]分別表示負大，負中，負小，零，正小，正中，正大。

在不同的和的取值大小時PID的三個參數都要滿足以下規則：

1)當e的值較大時，應取較大的Kp和較小的Kd同時取較小的Ki值；

2)當e的大小中等時，Kp值減小，Kd和Ki的大小要適中；

3)當e的值較小時，Kp與Ki都應取較大值。當|ec|出現較大時，Kd通常應取中等大小。

以PID中Kp、Ki、Kd三個參數的調整原則作為參考，在設計模糊自適應PID三個參數值時應充分考慮其整個系統運行的時變性，根據PID三個參數分別在控制過程中所起的作用以及它們之間的聯系。因此△Kp、△Ki、△Kd三參數自適應的規則表分別如表1～表3所示。

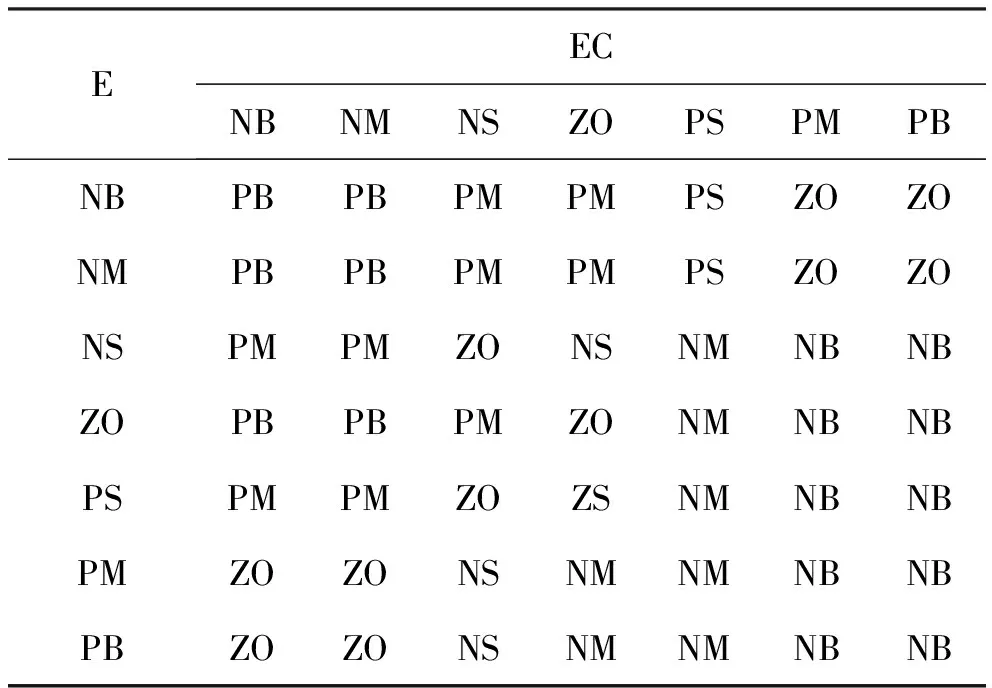
表1 △Kp的模糊規則表

表2 △Ki的模糊規則表

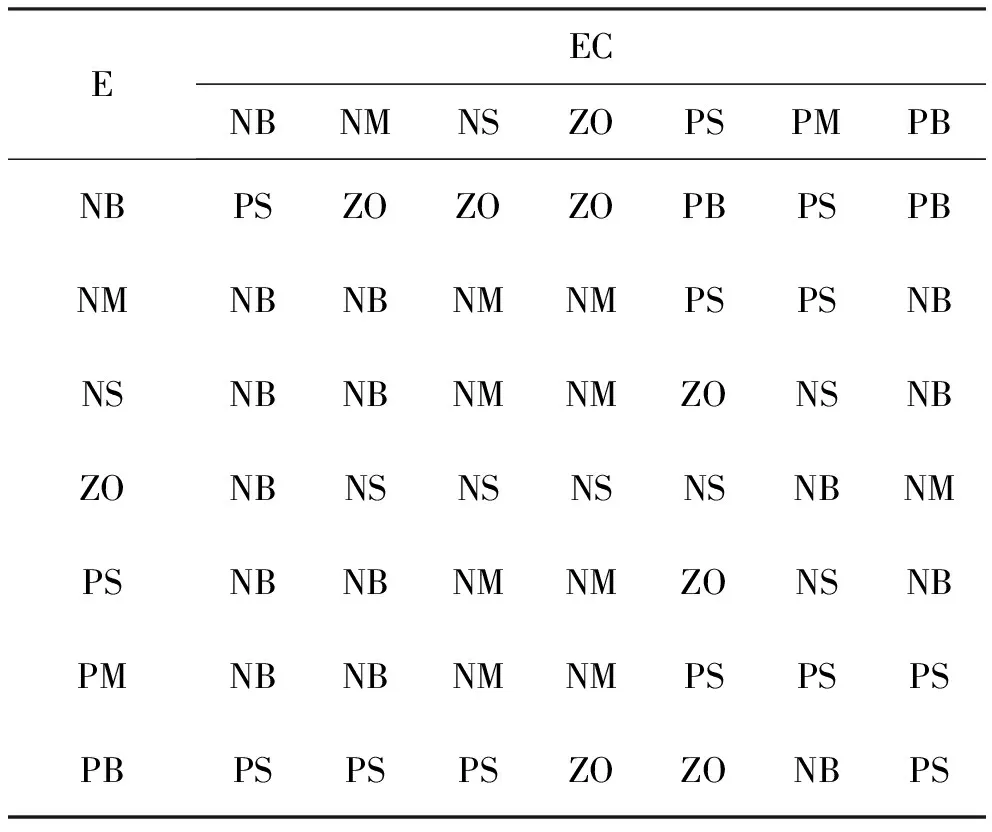
表3 △Kd的模糊規則表

本文提出模糊自適應PID變槳距控制器，其控制系統結構圖如圖5所示。

3 仿真實例

用于風力發電機組仿真的參數如下：空氣密度ρ=1.22 kg/m3，額定功率P=1 500 kW，額定風速Vr=7.602 7 m/s，風輪額定轉速Wr=19.8 r/min，切入和切出風速分別為3 m/s和25 m/s，葉輪半徑R=38.5 m，齒輪傳動比n=75.76，發電機同步轉速W1=1 500 r/min，發電機電壓690 V。

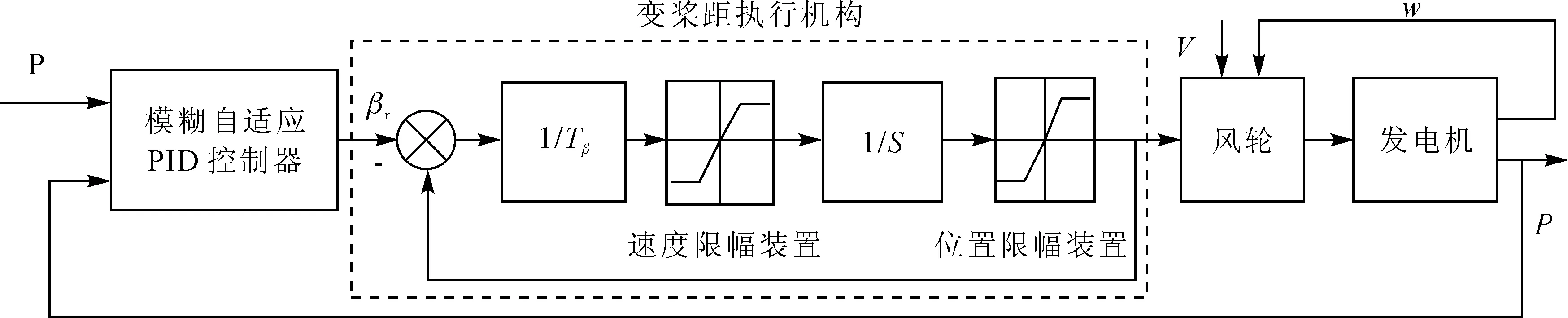
圖5 風力發電機變槳距控制系統結構

當風速變化曲線如圖6的時候，因為額定風速為7.6 m/s，所以此風速仿真曲線都高于額定風速為高風速，當風力發電機組在高風速運行的時候，此時風力發電機組的槳距角會打開從而達到控制風力發電系統的目的。圖7為PID控制的仿真結果，圖8為模糊自適應PID控制的仿真結果。

圖6 風速變化曲線

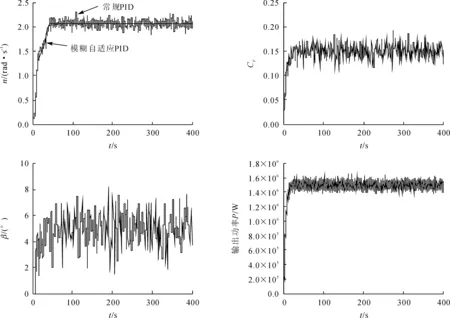
圖7 PID控制仿真結果

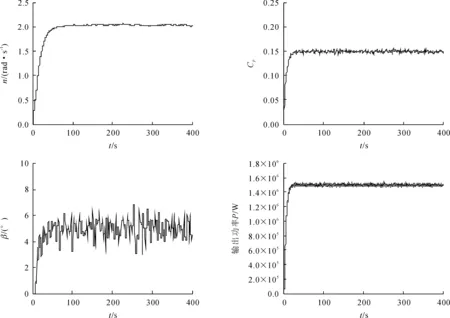
圖8 模糊自適應PID仿真結果

對模糊自適應PID控制的風力發電機，在高風速的情況下，模糊自適應PID控制器可以快速實現小范圍槳距角調節，輸出功率的波動也很小從而使系統更加穩定地運行。

通過仿真結果可知，得出相比PID控制，模糊自適應PID控制的變槳距，槳距角變化的幅值區間小，輸出功率較平穩，風輪轉速更穩定更趨近額定值，從而達到額定功率附近的穩定輸出。

4 結 語

由于整個風力發電系統是一個復雜的非線性系統，通過模糊自適應PID來控制變槳距和常規PID控制變槳距進行仿真比較，相較于常規PID的控制模糊自適應PID的控制提高了系統的靈活性和適應性，具有較好的抗干擾能力與魯棒性能，因其控制結構簡易使其在工業上具有優良的應用價值。