一種聯合LTR和社交網絡的Top-k推薦方法

熊麗榮，王玲燕，黃玉柱

1(浙江工業大學 計算機科學與技術學院，杭州 310023)2(浙江理工大學，杭州 310018)

1 引 言

推薦系統可以有效地應對信息爆炸問題，越來越多的研究者將其作為學術研究的重點[1].大量研究利用用戶-項目評分矩陣預測每個用戶對每個項目的評分值，這些工作致力于提高全局評分預測精度即降低評分預測誤差值，MAE和RMAE[2].推薦系統的最終目的是為目標用戶提供一個排序的項目列表，但最小化評分預測值并不總能得到較好的top-k列表[3，4].因此，本文更關注于基于top-k的推薦[5]而不是基于評分預測的推薦.

如何為用戶產生一個排序的項目列表被認為是Learning-To-Rank (LTR)[7]類問題，可以采用監督式的機器學習方法，從訓練數據中得到用戶特征信息，從而產生推薦結果.用戶-項目評分矩陣是top-k推薦系統中至關重要的內容，然而，在現實生活中用戶往往只會購買、評分小部分項目，這導致了top-k推薦系統由于缺少評分數據而不能產生較準確的推薦結果.另一方面相比于推薦系統產生的推薦結果，用戶更傾向于朋友推薦的項目.將社會化網絡中用戶間的信任信息結合到top-k推薦算法當中可以緩解數據稀疏問題的同時提高用戶對推薦結果的接受度.

本文結合社交網絡信息，提出一種基于LTR的top-k推薦算法，BTRank相比較于已有的工作，本文有如下幾個重要貢獻：

1) 提出了一種新的信任計算模型，可以對信任信息做預處理，從全局、局部等多個方面挖掘用戶間的潛在信任信息；

2) 考慮用戶興趣會隨著時間發生變化，設計了時間衰減效應模型，根據時間對用戶的評分數據進行處理；

3) 綜合考慮用戶對項目排序以及對信任用戶排序時展現出來的興趣偏好信息，構建用戶特征矩陣，最終得到top-k推薦列表.實際數據集上的實驗表明，本文的算法效果優于傳統推薦算法以及同類的top-k推薦算法.

本文第2章闡述了相關工作.第3章詳細介紹了本文提出的算法BTRank.第4章分析了本文算法的復雜性.第5章給出了實驗與結果分析.最后第6章總結全文并指出未來的進一步工作.

2 相關工作

2.1 推薦系統

個性化推薦系統很好地滿足了用戶對個性化服務的需求，目前比較成熟的個性化推薦算法包括協同過濾推薦算法、基于內容的推薦算法及混合推薦算法三大類.

基于內存的協同過濾通過使用皮爾遜系數[12]等方式來計算用戶間的相似度，并利用相似度過濾出近鄰集合，最后基于這些近鄰產生推薦結果.基于模型的協同過濾算法通過訓練得到相應的特征模型，在數據稀疏情況下算法效果優于內存類協同過濾算法.矩陣分解可以將一個高維矩陣分解為兩個低維特征矩陣的乘積，達到預測原矩陣空缺數據的效果，并且這兩個特征矩陣的維度取值遠遠小于原矩陣的維度，因此在眾多的模型類協同過濾算法中[17，25，26，30]矩陣分解是被最廣泛使用的.本文的算法BTRank中也采用了矩陣分解方法.

基于內容的推薦算法[13]根據產品的特征描述和用戶的購買歷史信息，向用戶推薦與他們購買過的產品有著類似特性的產品.一般適用于文本類的推薦，如新聞推薦、閱讀推薦等.基于內容的推薦算法推薦結果過度單一，導致目標用戶經常得到與曾經喜歡的項目類似的其他項目，推薦結果缺少多樣性.

混合過濾算法將多種個性化推薦算法進行融合[14，15]，然而目前還是不能很好的將協同過濾推薦和基于內容的推薦算法進行擬合，并且算法的時間復雜度和空間復雜度都比較高，往往不能很好地滿足實時性的推薦需求.此外，大多數的混合推薦算法都是基于假設用戶是獨立的個體的前提，忽略了社交網絡中用戶的朋友關系及信任關系，因此，準確度也不高.

以上三類算法是在目前的推薦領域內運用較為廣泛的方法，研究者們主要用這些方法解決兩大類問題：最小化評分誤差、優化top-k項目排序.

2.2 基于評分預測的推薦

在實際生活中，用戶往往只會購買并且評分小部分商品，所以用戶-評分矩陣存在大量的“0”分數據，即評分數據存在嚴重的稀疏性.盡管基于模型的協同過濾算法可以有效地緩解該影響但是并不能完全去除數據稀疏對算法效果的影響.近年來，隨著Facebook，Twitter等社交服務迅速發展，基于社會網絡的推薦系統得到了越來越多的關注，很多研究者將社會化網絡中的信任信息加入到推薦算法中以緩解用戶數據稀疏問題.Jamali等人[16]結合基于內存以及基于模型的協同過濾算法，利用信任信息提出了隨機走步框架.該算法可以在較短的路徑中得到更精準的評分預測值，同時還可以提高推薦結果的覆蓋率.Ma等人[17]首次提出了聯合概率矩陣分解(Unified Probabilistic Matrix Factorization，UPMF)方法，在方法的訓練模型中，評分矩陣和信任矩陣共享用戶特征矩陣，從而能夠結合這兩面信息進行推薦.

然而，用戶更希望看到一個符合自己興趣愛好的top-k項目推薦列表，上述算法主要致力于最小化評分預測誤差值RMSE和MAE，并不能得到一個更好的top-k排序列表.本文的研究重點在于如何找到一個更好的top-k列表.

2.3 基于top-k排序的推薦

已有的一些較好的top-k推薦方法，利用LTR算法思想[7]，從訓練數據生成個性化排名列表.基于LTR的top-k推薦方法分為list-wise和pair-wise兩類.Pair-wise模型通過用戶購買、瀏覽信息訓練其對每個項目對的相對偏好[18，19].Pair-wise模型在top-k推薦方面已經取得了實質性的改進，但存在著高計算復雜度的問題.List-wise模型具高可擴展性[19，20]和較低的計算復雜度，該模型是基于實際排序列表和預測列表之間的差距來優化預測每個用戶的項目排名推薦列表.

將社會化網絡中的信任信息加入到推薦算法當中，可以緩解評分數據稀疏性問題，同時提高推薦算法的準確度[8，9，21，30].文獻[9]中提出了一種基于pair-wise的LTR方法，該文主要基于以下假設：相比于用戶根本不知道的項目，他們更傾向于其朋友喜歡的項目.然而，他們的方法不能直接處理數字評分，并且由于pair-wise模型的內在特性，該算法具有較高的計算復雜度.Yao等人[8]采用文獻[22]中的評分模型，將用戶的興趣愛好和其朋友的興趣愛好線性結合，建立了評分預測模型.與本文一樣他們也通過使用top-one概率(這將在本文第3章中解釋)來降低算法的復雜度.然而，他們只關注用戶對物品評分時存在的興趣偏好，忽略了用戶對朋友進行信任打分時展現出來的興趣偏好信息.Park[21]等人 中提出了TRecSo算法，從信任、被信任兩種角色來考慮用戶的特征向量，同時也將信任信息對top-k排序列表的影響考慮進算法當中，構建了一個出色的訓練模型.但是該算法對于用戶間信任處理過于簡單，只考慮了用戶的出度、入度信息，同時由于TRecSo模型中用戶特征向量由多個向量組成，導致模型的訓練復雜度有所上升.

在本文中，我們結合評分、信任信息提出了基于list-wise思想 BTRank算法.在算法模型訓練前期我們將從多方面來重組用戶間的信任信息，模型訓練時使用top-one概率來優化算法的性能.最后我們在兩個現實世界數據集上證明，BTRank要優于以上幾類優秀的方法.

3 基于信任的top-k算法BTRank

為了更好地了解本文提出的算法，本章中3.1節簡短的介紹核心top-one概率模型，3.2節中提出本文的時間效應模型，之后3.3以及3.4節分別介紹如何在評分、信任信息中應用top-one概率模型.最后3.5節展示如何結合評分、信任兩部分信息，給出BTRank模型的目標函數.

3.1 Top-one概率模型

Plackett-Luce模型[23]可以用于計算每個用戶對曾經評分過項目的排列分布概率.該模型基于假設：每個不同的項目排列都有相應的分布概率，而高的排列概率意味著該項目排序更受用戶喜愛.

排列概率：對于用戶ui，給定含有M個項目的集合V，π={v1，v2，…，vM}是其中一種可能的項目排序，其對應的評分信息為{ri1，ri2，…，riM}，那么π排列的分布概率為：

(1)

其中rij是用戶ui對項目vj的評分值，exp(r)=er.根據公式(1)可知，對于含有M個項目的集合來說，每個用戶都有M!種不同的項目排序，計算復雜度太高.為了解決這個問題，我們使用top-one 概率來代替公式(1)中的排列分布概率：

(2)

由于用戶更關心系統推薦給他的top-k個項目，因此本文在考慮項目可能排序時只關注前k個項目.公式(2)代表對于用戶ui來說項目vj被排列在第一位的可能性.

3.2 時間效應模型

傳統的推薦算法，將所有的項目平等對待，沒有考慮用戶的興趣會隨著時間的演變產生變化，致使推薦精度不高.根據19 世紀德國心理學家赫爾曼·艾賓浩斯的實驗結果可得知，遺忘在記憶后會立刻開始，并且遺忘速率遵循先快后慢的規律.他根據實驗結果將時間與記憶量的關系繪制成了著名的艾賓浩斯遺忘曲線[29]：

圖1 艾賓浩斯遺忘曲線Fig.1 Ebbinghaus forgetting curve

學者Ding也認為資源的時效性隨時間的變化應是一種指數衰減的過程[28]，因此結合圖1我們設計資源衰減的時間效應模型為：

h(Δt，λ)=e-λΔt

(3)

其中Δt∈[0，+∞)表示學習過后經過的時間，λ代表遺忘速率，不同人群的λ可能不同，h為到目前位置記憶的衰減比例.用戶可以分為兩類：

1)念舊型，喜歡一類事物的周期很長，一段時間內興趣愛好變化不大；

2)多變型，喜歡嘗試新事物，興趣愛好隨時間呈現跳變型.在推薦系統中，評分信息可以很好的反映一個人的興趣愛好變化，本文以3個月為一個周期，統計用戶從第一次評分到目前為止所有周期內平均評分的變化值作為該用戶的遺忘速率λ.

3.3 評分模型

基于矩陣分解框架，用戶ui對項目vj的預測評分計算方法如公式(4)所示：

(4)

但是公式(4)中并未考慮時間因素對用戶評分的影響，考慮時間效應后，改寫公式(4)，得到用戶ui在時間ti，j對項目vj的預測評分計算公式：

(5)

同時為了解決用戶評分數據的稀疏性，本文在計算預測評分的模型中加入信任用戶間的影響，更新公式(5)如下所示：

(6)

sik表示用戶ui對uk的信任評分值，T(i)是用戶ui信任的用戶集合.參數β用于平衡控制信任用戶對目標用戶評分的影響程度，β∈[0，1].當β=1時表示完全沒有影響，反之β=0表示用戶對項目評分完全受信任用戶影響.

此時我們可以利用公式(2)的top-one 概率模型以及交叉熵公式得到目標函數，最小化預測排序列表與真實排序列表間的不穩定性：

(7)

3.4 信任模型

本文提出了一種新的信任計算模型，使用全局、局部兩個方面來刻畫用戶間信任信息.在計算對來說uj的全局信任gtij時，不同于已有的研究，本文主要考慮以下三點：

1) 其余所有用戶對uj的信任評價值；

2) 對uj有信任評價的用戶數量：

3)ui與這些用戶之間的興趣相似度.最終本文構建全局信任計算公式如下所示：

(8)

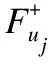
本文在計算與uj的局部信任ltij時，分兩種情況進行考慮：

1)對uj有信任評分值，即對uj存在直接信任，那么對uj間的局部信任基于直接信任進行計算得到；

2)對uj沒有信任評分值，根據信任傳播性得到對uj的間接信任值作為局部信任值.為了消除用戶間評分的習慣差異性，本文對數據集中用戶間的直接信任評價值進行以下處理：

(9)

(10)

本文主要利用信任傳遞性來計算用戶間間接信任評價值idtij.公式(11)為信任衰減函數，L是信任傳遞路徑長度，其中最大路徑長度Max_Hop<=6：

(11)

本文選取最有效路徑[6]而不是最短路徑作為用戶間最佳的信任傳播路徑.同時將網絡中所有用戶間平均信任值作為判斷的信任閾值Υ.當某條路徑上存在兩個相鄰用戶間的信任評價值小于Υ時，則放棄該條路徑重新尋找有效路徑.某條路徑Pathi的源節點ui對目標節點uj的信任評價值計算如公式(12)所示：

(12)

其中uk代表路徑Pathi中第K個節點，Tuk-1→uk表示節點uk-1對uk的信任評價值，當信任值大于閾值Υ時，Iuk-1→uk為1，反之為0.當網絡中存在多條有效路徑時，本文選取信任值最大的一條，如公式(13)所示：

(13)

綜上所述，用戶間的最終信任值計算公式如(14)所示，其中α∈[0，1]為平衡參數，用于調和全局信任以及局部信任間的比重.

sij=αgtij+(1-α)ltij

(14)

當用戶ui對uj只存在間接信任關系，考慮到此時的局部信任比全局信任要可靠的多，特別是在全局網絡中對uj有過信任評分的用戶數量稀少的情況下.所以此時α的計算公式如下所示：其中F+(uj)表示網絡中信任uj的用戶集合.

(15)

以上是本文提出的信任模型的全部內容，它主要用于對信任的前期處理，對于訓練過程中ui對uj的信任值可以根據公式(16)構建：

(16)

Ui是用戶ui的特征向量，Tj是用戶uj的信任特征向量.同樣地，對于用戶間信任評分數據也可以用熵公式來衡量真實訓練排序以及預測排序之間的差異，最小化熵公式如下所示：

(17)

3.5 目標函數

在3.3、3.4節中，本文定義了如何將評分、信任信息模型化，最后本文使用公式(18)將公式(7)與公式(17)聯合進一個統一模型當中，并將其作為目標函數：

(18)

為了降低模型復雜度，本文設置λu=λv=λt=λ.同時為了得到相應的特征向量，本文采用隨機梯度下降法來得到它們的局部最優值，其計算公式如下所示：

(19)

(20)

(21)

(22)

(23)

(24)

(25)

(26)

其中g′(x)是邏輯斯蒂函數g(x)的導數，g′(x)=exp(x)/(1+exp(x))2.

4 復雜性分析

BTRank的計算開銷主要來自于公式(14)中前期信任關系的訓練、公式(18)中目標函數L的計算以及公式(19)-(26)中各個特征向量對應的梯度下降的計算.在訓練信任關系時，我們假設存在信任數據的用戶數量為t，且每個用戶的鄰居集合大小為N，則間接信任關系的訓練時間復雜度為O(t2N)，其中N通常較小，可以認為是常數，則時間復雜度趨向于O(t2)；目標函數L的時間復雜度為O(pRl+pSl)，其中pR，pS分別表示矩陣R，S中非零元素個數，由于數據稀疏性，pR和ps都很小；梯度下降法中計算復雜度主要由公式(19)-(21)產生，其時間復雜度分別為O(pRk+pSk)，O(pRk)和O(pSk)，k表示最終推薦給用戶的top-k目表中的項目個數，因此每次迭代的總時間復雜度為O(pRk+pSk).假設本文算法迭代d次，總的時間復雜度為O(t2)+O(dpRk+dpSk)，因此，與pair-wise的LTR方法不同，我們提出的模型可以有效地應用到大規模數據集中.

5 實驗與結果分析

在本章節中設計了幾個實驗將本文的算法BTRank與其余幾個出色的算法進行比較.實驗的設計主要基于以下幾點：

1.如何將本文算法與已有優秀算法進行比較？

2.考慮時間因素是否可以提升算法的精度？

3.模型訓練前使用第3.4節中提出的信任模型對信任數據做處理是否對算法有所幫助？

4.參數β對算法推薦準確率有怎樣的影響？

5.特征向量U、V、T的維度取值對推薦準確率有什么影響？

5.1 數據集

在實驗中，我們使用兩個公共現實世界的數據集Epinions*http://www.trustlet.org/wiki/Extended_Epinions_dataset和Ciao*https://www.librec.net/datasets.html，每個數據集都包含用戶項目評分、用戶之間的信任關系(數據集中的信任關系都是不對稱的)和評分的時間信息，其中項目評分是區間[1，5]內的整數.

5.2 實驗規則

對于每位用戶我們分別隨機選取n=10，20，50條項目評分和信任記錄作為訓練數據集，余下的都作為測試數據.為了保證每位用戶至少存在10條測試數據，我們會相應的過濾掉數據記錄少于20，30，60條的用戶.

參數設置：對于所有的對比實驗，本文均按照原文設置最優參數；在算法BTRank中，我們設置λ=0.1，γ=0.01，其中γ是迭代過程中的學習速率，所有的實驗結果都是5次實驗的平均值.

5.3 評價函數

均方誤差(RMSE)和平均絕對誤差(MAE)是傳統推薦系統的標準評估指標，這兩個指標能衡量真實評分與預測評分之間的差距，但是不能是評價top-k項目列表排序準確性.本文旨在提高top-k推薦質量，因此使用信息檢索領域最常用的指標NDCG、Recall、Precision作為本文評價標準.

NDCG更加重視排序列表的前幾位，排序越前面的項目在評估中所占比重越大.對于排序在第一位的項目來說，得到5分與得到4分評分相比，前者的NDCG@1更高.所以對于ui來說，k個項目排序列表的 NDCG值為：

(27)

其中Z是一個常量，它使對于ui來說最優的top-k排序的NDCG為1.

最后我們計算所有用戶的NDCGi@K值并取平均值得到NDCG@K如下所示：

(28)

其中|U|是用戶集合U的大小.

Precision@K表示推薦精準度，Recall@K表示召回率，對于ui，集合Pi={v1，v2，…vK}表示由推薦系統產生的top-k項目列表，Qi={v1，v2，…vz}表示實際用戶偏愛項目，則

(29)

(30)

5.4 對比實驗

本文跟以下三類出色的推薦算法對比：傳統CF方法，僅基于評分的LTR方法和基于社交網絡的LTR方法.

a)傳統CF方法

UserKNN[27]：一種基于用戶相似度的傳統協同過濾推薦算法.

b)基于評分的LTR方法

BPR[18]：結合矩陣分解方法的pair-wise類LTR算法.

ListRank[19]：結合矩陣分解方法的list-wise類LTR算法.

c)基于社交網絡的LTR方法

SBPR[9]：在BRP的基礎上加入信任信息，提高算法準確度.

SoRank[8]：結合信任信息的list-wise類LTR算法，線性結合信任用戶對目標用戶的影響，從而優化top-k推薦算法效果.

BTRank：本文提出的算法.

5.5 信任模型的作用

為了驗證3.4節中提出的信任模型的有效性，我們設計了多個對比實驗，將本文算法BTRank與未應用信任模型的BTRank進行比較，實驗結果如圖2所示.從圖中可以看出，在各種情況下使用了信任模型的算法結果明顯好于未使用的算法結果，證明了本文信任模型對算法有推進作用，在算法訓練之前對信任數據做預先處理是必要的.

5.6 時間效應模型的作用

本文在3.2節中，根據艾賓浩斯遺忘曲線提出了一個時間效應模型，對用戶的評分數據根據歷史時間給予相應的權重，越接近當前時間的評分數據其權重值越高，反之則越小.

為了驗證該模型的有效性，我們設計了多個對比實驗將本文算法BTRank與未應用該時間效應模型的BTRank進行比較，實驗結果如圖3所示.從圖中可以看出，在各種情況下使用了時間效應模型的算法結果明顯好于未使用的算法結果，證明了該模型對算法有推進作用，考慮用戶評分數據時間效應性是有必要的.

圖2 信任模型的影響Fig.2 Impact of trust model

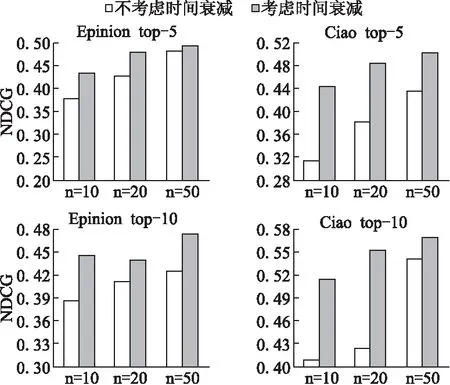
圖3 時間模型的影響Fig.3 Impact of time attenuation model

圖4 參數β的影響(n=20，k=5)Fig.4 Impact of parameter β (n=20，k=5)

5.7 參數β的影響

在文本算法BTRank中參數β用于控制信任用戶興趣愛好對項目評分的影響.本次實驗訓練數據選取規則采用n=20，結果如圖4所示.在不同數據集上算法效果趨勢各不一致，但是大體上都呈先上升后下降趨勢.其中β=0.4是一個閾值，當β<0.4時，算法效果呈上升趨勢，β>0.4時算法效果呈下降趨勢，所以此時將β值設為0.4使得算法效果最優.

5.8 特征維度的影響

矩陣分解算法復雜度隨著特征維度取值增加而增加，本文為了降低模型訓練的時間，在區間[1，50]上探尋局部最優的維度取值，實驗結果如圖5所示.根據結果可以看出，雖然算法效果趨勢都不完全一致，但是都呈先上升后下降的趨勢，在特征維度值取為5的時候達到最佳效果，所以在本文之后的實驗中我們將維度設置為5.

圖5 特征維度取值影響(n=10，k=5)Fig.5 Impact of latent dimensionality (n=10，k=5)

5.9 算法比較

為了驗證本文算法的有效性，本實驗將BTRank與其余五個算法進行比較，結果如圖6所示.從圖中可以看出本文算法BTRank的效果在各種不同情況下普遍好于其余算法，而UserKNN算法效果明顯弱于其它算法，很好地說明傳統的個性化推薦算法并不適用于top-k推薦.

BTRank、SoRank、ListRank-MF均是基于list-wise的LTR類算法，其中ListRank-MF算法未考慮信任用戶對目標用戶的影響，而SoRank和本文算法均考慮到了信任關系的影響，并且從實驗結果中可以明顯看出這兩個算法效果好于ListRank-MF，說明同時考慮自身以及朋友因素對評分構成的影響可以有效提升算法的效果；相比于SoRank，本文算法不但考慮用戶對項目排序展現出來的興趣偏好，同時聯合考慮用戶對朋友信任排序時的偏好信息，從而構建更準確的用戶特征矩陣.從這兩個算法的對比效果可以看出本文算法明顯好于SoRank，可見綜合考慮用戶對項目、朋友排序時的偏好可以有效提高算法效果.

其中BPR以及SBPR均是基于parie-wise的LTR類算法，這兩個算法與BTRank、SoRank、ListRank-MF對比，雖然整體效果要弱于list-wise類算法，但是并不明顯，說明pair-wise在top-k推薦中也獲得了較好的效果，但是相比于list-wise類算法還是略遜一籌.

6 總結與展望

本文提出了一種基于信任的LTR類推薦算法BTRank，通過加入社交網絡中信任信息來緩解數據稀疏問題、優化top-k排名預測精度.具體來說，本文首先使用信任模型重構用戶間的信任信息，其次設計時間衰減函數分階段評估用戶興趣變化，同時在預測用戶評分時考慮信任用戶對目標用戶的影響，最終結合用戶對項目評分排序以及對其他用戶信任評分排序時產生的偏好信息，構建更準確的用戶特征矩陣從而得到較好的top-k推薦列表.綜合實驗結果表明，BTRank推薦的top-k項目列表在準確度方面顯著優于傳統的推薦算法以及同類top-k推薦算法.

圖6 不同算法效果對比Fig.6 Comparison of different algorithms

為了降低算法的復雜度，本文提出的BTRank是基于項目top-one 概率而不是top-k概率.在未來的工作中可以研究更好的項目排序概率模型用于top-k排序推薦；其次希望可以研究出更好的時間衰減模型，能更準確地衡量評分數據十分稀少的用戶興趣變化.