多層平板一維非穩態導熱問題的數值解法

(吉林化工學院 石油化工學院，吉林 吉林 132022)

現實生活和實際生產中存在大量的非穩態導熱問題，如室內環境通過墻壁向室外的熱量傳遞過程、鍋爐內部通過壁面向外界的熱量傳遞過程以及埋地原油管道向周圍土壤的散熱過程等。由于非穩態導熱問題中物體內部溫度隨時間而變化，因此求解起來比穩態導熱要復雜得多。即使是最簡單的一維問題，最簡單的初始條件和邊界條件，其解析解的形式也相當復雜，將其應用于實際問題的求解中將存在一定的困難。在解決導熱問題時主要有理論分析法、實驗方法及數值計算方法等，其中數值解法隨著計算機硬件水平的大幅度提高和計算方法的完善，逐漸受到人們的重視。下面我們將針對多層平板一維非穩態導熱問題的數值解法進行介紹。

1 提出問題及問題分析

1.1 提出問題

由多層材料組成的無限大平板，兩側分別置于溫度恒定的高溫和低溫環境中，兩側環境溫度分別為Th和Tl，且Th>Tl，各層材料的厚度及物理性質如熱導率、比熱容、密度等已知，如圖1所示。由于高溫側環境溫度過高，無法測量高溫側表面溫度Twh，低溫側表面溫度Twl可實時監測，可以獲得低溫側各個時刻的表面溫度。需確定各層材料中的溫度分布情況。

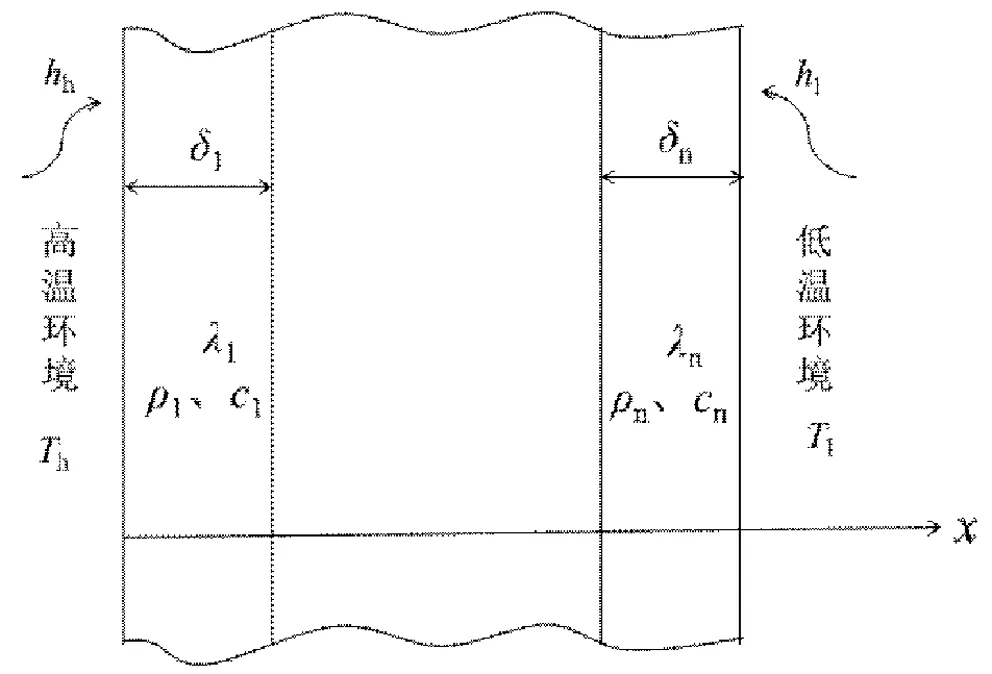
圖1 多層平板導熱示意圖

1.2 問題分析

對于以上問題的傳熱過程，熱量是由高溫環境通過多層無限大平板向低溫環境傳熱的過程，傳熱環節包括：高溫環境與平板高溫側的對流傳熱(高溫環境溫度Th已知，平板高溫側溫度t(0,τ)未知，對流傳熱系數hh未知)；平板高溫側通過各層平板向平板低溫側的導熱(各層平板的厚度及熱導率、比熱容、密度已知，平板內及各平板的接觸面溫度未知)；平板低溫側與低溫環境間的對流傳熱(低溫環境溫度Tl已知，平板低溫側溫度t(δ,τ)已知，對流傳熱系數hl未知)。可認為垂直于X軸的任一平面內溫度均勻，因此可看成是一維導熱問題，且溫度隨時間變化，為非穩態導熱問題。

2 數學模型及邊界條件

2.1 數學模型

如圖1所示的導熱問題，可通過對直角坐標系的導熱微分方程(1)去掉Y、Z兩個方向的溫度二階導數及內熱源項，簡化得到微分方程(2)

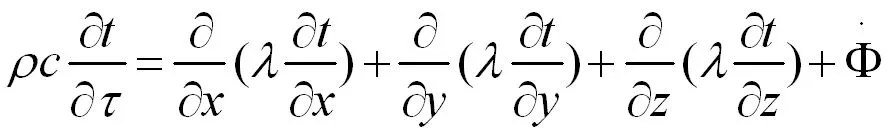
(1)

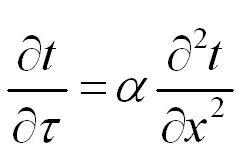
(2)

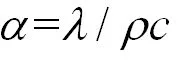
2.2 邊界條件

上述三個公式中，t(x,τ)表示x位置處τ時刻的溫度，δ為多層平板的總厚度。

3 數值解法及穩定性分析

3.1 數值解法

將一維非穩態導熱微分方程(2)在空間及時間上進行離散處理，將等號左邊非穩態項取向前差分，將等號右邊擴散項取中心差分，則有[1]。

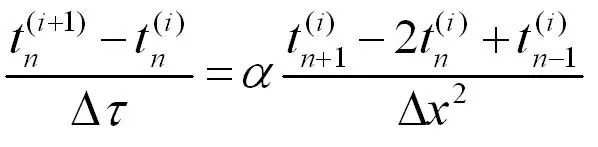
(3)

上式可改寫為

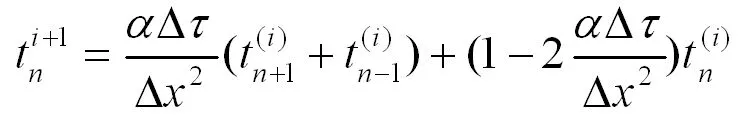
(4)

兩層材料接觸點處溫度計算采用下式[2]：

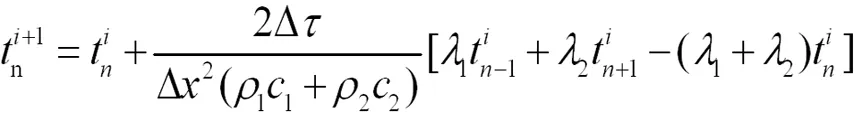
(5)

上述為一維非穩態導熱問題的顯式差分格式數值解法，其優點是計算工作量較小，缺點是對時間步長和空間步長存在限制。其求解過程是從已知初始溫度分布出發，根據邊界條件依次求得以后各個時層上的溫度分布情況。

3.2 數值穩定性分析

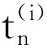
如果把計算區域用N個節點將其等分，則節點0和N為對流傳熱面，與微分形式的數學描寫相對應的顯式離散形式為

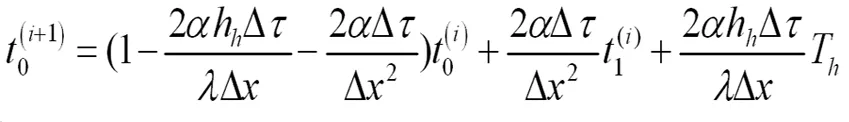
(6)

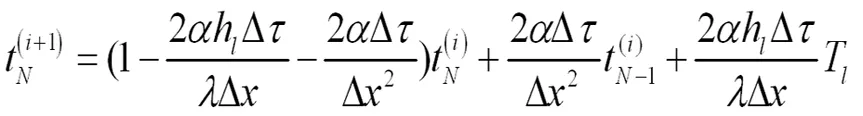
(7)

3.3 程序設計

由于邊界節點溫度是隨時間而變化的，兩側的對流傳熱系數也是未知的，這就需要采用逐步逼近法編程求解平板內的溫度分布情況。雖然邊界節點溫度是變化的，但是當達到穩定狀態后，平板內及邊界節點溫度均會達到一恒定值。而低溫側邊界節點溫度是可以通過實驗測定的，如果知道高溫側邊界節點溫度，那么問題就可以進行求解。因此我們按照如下步驟進行編程：

(1)給定平板的初始條件。

(2)假設達到穩態時的高溫側邊界節點溫度Twh(達到穩態時，高溫側邊界節點溫度接近高溫環境溫度)，低溫側邊界節點溫度已知，可通過串聯熱阻疊加原則，計算出兩側的對流傳熱系數。

(3)將對流傳熱系數帶入式(6)、(7)確定邊界節點溫度。

(4)根據邊界條件，利用式(4)、(5)分別確定各層平板內部以及兩層平板接觸面處的溫度值。

(5)循環執行第(3)、(4)步，直到達到穩定狀態，確定高溫側邊界節點溫度Twh1，若|Twh-Twh1|小于允許誤差，則退出并輸出數據；否則令Twh=Twh1，繼續執行步驟(2)。

4 結論

上述數學模型及時間-空間的離散顯式格式，主要用來解決多層平板的一維非穩態導熱問題，可以用來確定任意時刻平板內的溫度分布情況，也可以用來計算各個時刻通過平板的導熱量。通過公式(5)可以有效的處理多層平板接觸處的節點溫度計算；公式(6)、(7)用來處理平板兩側均為對流傳熱的邊界節點計算問題；對于顯示差分格式，時間和空間步長要滿足一定的限制條件，文中也進行了詳細的分析，并給出了需滿足的計算條件；最后給出了兩側對流傳熱系數未知情況下的編程詳細步驟，為實際生產和生活解決此類問題提供了理論依據和解決方法。