積極思維定式下的數(shù)學思維培養(yǎng)

高傳敏

[摘要]思維定式對學生的數(shù)學學習既具有積極作用又具有消極作用。作為教師，要充分發(fā)揮思維定式的積極作用，培養(yǎng)學生的類推思維、發(fā)散思維和創(chuàng)新思維，引導學生突破思維定式對思維的規(guī)約、鉗制，掙脫思維定式的枷鎖，發(fā)展學生的數(shù)學思維，提升學生的數(shù)學核心素養(yǎng)。

[關(guān)鍵詞]思維定式;積極遷移;小學數(shù)學

[中圖分類號]

G623.5

[文獻標識碼]A

[文章編號] 1007-9068（ 2019）35-0080-02

教育心理學研究表明，學生的學習往往是基于自身已有前理解、前經(jīng)驗以及自身學習習慣、思維方式等展開的。學生的這種前理解、前經(jīng)驗所形成的學習心理準備狀態(tài)對學習會產(chǎn)生雙重性影響：其一就是有助于學生的數(shù)學學習，產(chǎn)生積極的正遷移作用;其二就是容易形成思維定式，從而阻礙學生的數(shù)學學習，束縛學生的數(shù)學思維，尤其是發(fā)散性、多向性、創(chuàng)造性思維的發(fā)展。教學中，教師通過對學生學情的了解、分析，設(shè)計符合學生最近發(fā)展區(qū)的導學流程，可以充分發(fā)揮其思維定式在新的學習中的積極作用，促進學生有效形成良好的思維品質(zhì)和學習能力。

一、在思維定式的積極認知遷移幫助下發(fā)展學生類推思維

蕭伯納認為，我們的教育期待的是培養(yǎng)“主動追求知識的兒童”，而不是被知識困囿、受限制的兒童。學生先前所形成的思維定式中最有價值的地方就是合情推理、積極遷移。教學中，教師應充分發(fā)掘與新知相關(guān)的學生已有認知，從而在此基礎(chǔ)上自然橋接、主動生成，讓學生的思維得到充分發(fā)展，使解決問題的策略得到豐富和提升。通過認知遷移，不僅有助于培養(yǎng)學生發(fā)現(xiàn)新舊知識的關(guān)聯(lián)性，讓學生學會舉一反三、觸類旁通，發(fā)展類推思維，繼而降低學習難度，還有助于學生完善數(shù)學認知結(jié)構(gòu)，建構(gòu)數(shù)學知識的整體結(jié)構(gòu)等。

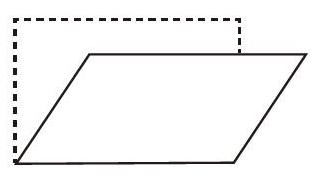
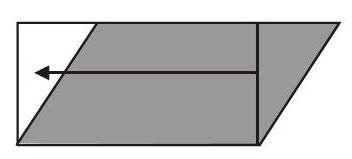
如在教學“平行四邊形的面積”（蘇教版教材五年級上冊）時，筆者以復習長方形的面積計算為導人，然后給學生呈現(xiàn)長方形被拉升和壓縮后的變化軌跡圖，讓他們直觀感受到長方形和平行四邊形之間互相轉(zhuǎn)化后，面積發(fā)生了變化。接著，再通過擺小正方形的方式來計算長和寬分別是6厘米和4厘米的長方形變成平行四邊形后的面積，看看結(jié)果是否相同。這樣，學生從動態(tài)想象、直觀猜想到實際計算，在頭腦中確定了“長方形被壓縮后面積會變小”的結(jié)論，而后再次展開動態(tài)想象：長方形被拉升或壓縮后變成了平行四邊形，那么，平行四邊形可不可以轉(zhuǎn)化成長方形呢？眼尖的學生立刻發(fā)現(xiàn)將平行四邊形“一邊”的三角形切割下來，移到形一邊，就可以湊成一個新的長方形。這樣，平行四邊形的面積依然可以用長方形的面積計算公式來計算。

在這樣的積極思維定式的推動下，學生的轉(zhuǎn)換思維得到了發(fā)展，學生在輕松習得平行四邊形面積計算方法的同時，觀察、比較、推理、歸納的能力也得到了培養(yǎng)和提高。學生不僅認識到，通過剪拼可將平行四邊形轉(zhuǎn)化成長方形，還發(fā)現(xiàn)，用推拉法進行轉(zhuǎn)化，前后的圖形的周長沒有變，面積卻發(fā)生了變化;而通過剪拼法進行轉(zhuǎn)化，前后的圖形的面積沒有變化，周長卻發(fā)生了變化;等等。這里，思維定式催生了學生的探究方法，并且讓學生明晰了兩種方法之間的差異，將學生的數(shù)學學習引向深入。

二、在思維定式的積極整合運用幫助下發(fā)展學生發(fā)散思維

學生的天性就是好奇、樂探索、勤發(fā)現(xiàn)。在學生的知識結(jié)構(gòu)中蘊藏著大量的可利用的資源，這些資源有時會內(nèi)化為學生的一種思維定式。教學中，教師要充分發(fā)掘、運用學生認知結(jié)構(gòu)中的資源，引導學生展開積極的交流、研討，通過適當?shù)淖穯枺蜷_學生的數(shù)學思維，催生學生的數(shù)學想象，從而將學生的思維定式喚醒、激活，進而主動建構(gòu)數(shù)學知識。在這個過程中，學生的數(shù)學學習將從膚淺走向深刻、從狹隘走向廣闊。在課堂上，教師要“讓學于生”，讓學生自己整合、運用已有知識自主探究、發(fā)現(xiàn)，從而在經(jīng)歷知識誕生的過程中享受發(fā)現(xiàn)的無限愉悅。

如在教學了圓柱和圓錐的體積計算公式后，筆者出示學生熟悉的正方體和長方體，引導學生在猜想中發(fā)散思維，以加深對極限思想的理解：“我們知道了圓柱體的體積可以用底面積乘高，也就是‘V=Sh來計算。那么，正方體和長方體的體積能否也用這個公式來計算呢？”學生陷入短暫的沉思之后，很快有人舉手回答：“公式v=Sh中的底面積S，其實就是長乘寬得來的呀！V長=abh=Sh，V正=a2h=Sh。”“長方體可以看成是無數(shù)個大小、形狀完全相同的小長方形堆積而成的，用一個長方形的面積乘堆積的高度，就是這個長方體的體積了！”“正方體也可以這么理解。”筆者乘勢追問：“那么，底面積是三角形的三棱柱呢？也可以用底面三角形的面積去乘高來計算體積嗎？”學生稍加思索后近乎異口同聲地答道：“也可以這么來算！底面是五邊形、六邊形、八邊形、十二邊形等上下粗細相等的柱體，它們的體積都可以用‘底面積乘高來計算，即‘V=Sh。”

課堂上，學生的猜想興趣被點燃，好奇心被激起，他們由圓柱體積計算的認知推及其他形體的體積計算，從而認識到體積計算的本質(zhì)，感受到極限思想，思維的深度和廣度都得到了充分的發(fā)展。在這個過程中，單個數(shù)學知識“點”的探究方法被拓展、延伸為一“類”數(shù)學知識的探究方法。數(shù)學知識“點”由此上升為具有強大包攝力、內(nèi)生力、再發(fā)力和生長力的“大概念”“高觀點”，這是一種更為上位的數(shù)學認知。這種數(shù)學認知不僅將眾多的數(shù)學知識整合成一種具有廣泛遷移性的思想方法，而且內(nèi)化為學生的數(shù)學核心素養(yǎng)，成為學生學習力要素的重要組成。

三、在思維定式的積極反思對比幫助下發(fā)展學生創(chuàng)新思維

培養(yǎng)學生靈活、深刻、敏銳、批判、創(chuàng)新的數(shù)學思維，是小學數(shù)學教學的永恒追求。美國學者恩尼斯提出從低階思維到高階思維的標準是：學生的抽象思維得到發(fā)展和運用;能夠?qū)⑿畔⑦M行有機整合;能夠運用合理的邏輯和判斷準則。在數(shù)學教學中，教師可以通過變化題目的條件、問題等，來發(fā)展學生的求異思維、變通思維、發(fā)散思維。只有通過變換條件、問題等引導學生對比反思，才能有效地發(fā)展學的批判思維和創(chuàng)新思維。

如教學六年級上冊“百分數(shù)”時，對拓展練習題：“一工程隊在修筑一條長30千米的城市四車道道路時，前兩天修了全程的16%，照這樣的速度，他們修完這條路還需要多少天？”一些學生列出了“30÷（ 30x16%÷2）”這樣的錯誤算式。為了讓學生自己發(fā)現(xiàn)錯誤，筆者即時追加問題：“修完全程一共花了多少天？”學生在對比解答中很快發(fā)現(xiàn)審題時犯了經(jīng)驗主義錯誤，對嚴謹審題有了正確的認識。筆者再順勢引導他們深入思考：“能否結(jié)合百分數(shù)來確立各數(shù)量之間的關(guān)系，進行更加簡潔的運算？”在一番思考后，一些思維敏捷的學生迅速意識到可以將道路的總長度看作單位“l(fā)”，進而給出了“1÷（ 16%÷2）-2”“2x[ （1-16%）÷16%]”等多樣化的簡便算法，這些算法顯現(xiàn)出學生的簡約思路。而后，筆者再引導學生本著求簡思想探究出了“2÷16%-2”這樣的至簡算法。

可見，思維定式是一把“雙刃劍”。在教學中，教師既要合理地利用學生思維定式積極的一面，促進學生的數(shù)學學習，又要警惕思維定式的消極影響，引導學生突破思維定式對思維的規(guī)約、鉗制，掙脫思維定式的枷鎖。只有這樣，才能促進學生對數(shù)學知識進行主動建構(gòu)，讓學生的數(shù)學思維不斷地從低階邁向高階，從而提升學生的數(shù)學學習能力，發(fā)展學生的數(shù)學核心素養(yǎng)。

（責編羅艷）