陣列測(cè)量中的卡爾曼濾波器算法
季建朝,張宇,趙子龍,夏露
?
陣列測(cè)量中的卡爾曼濾波器算法
季建朝1,2,張宇2,趙子龍2,夏露2
(1. 清華大學(xué)航天航空學(xué)院,北京 100084;2. 陸軍航空兵學(xué)院,北京 101123)
針對(duì)經(jīng)典波束形成算法不具備實(shí)時(shí)性、占用存儲(chǔ)空間大、計(jì)算速度慢等缺點(diǎn),提出了基于卡爾曼濾波器的算法。這種算法將信號(hào)處理領(lǐng)域中現(xiàn)有的卡爾曼濾波器理論與陣列信號(hào)處理過(guò)程相結(jié)合,在頻域內(nèi)對(duì)聲學(xué)陣列所采集到的數(shù)據(jù)進(jìn)行迭代處理,不僅能夠及時(shí)發(fā)現(xiàn)風(fēng)洞測(cè)量中存在的各種問(wèn)題,而且可以實(shí)時(shí)消除由測(cè)量環(huán)境所引起的各種誤差。仿真結(jié)果表明,這種算法比經(jīng)典波束形成算法收斂速度更快,不僅成像效果很好,而且能夠?qū)Φ退龠\(yùn)動(dòng)聲源進(jìn)行定位。此算法具備實(shí)時(shí)性,為風(fēng)洞聲源的實(shí)時(shí)定位提供了重要的算法選擇。
氣動(dòng)噪聲;陣列信號(hào)處理;波束形成;迭代方程
0 引言
隨著交通運(yùn)輸、工業(yè)生產(chǎn)、城市建筑等的快速發(fā)展,噪聲污染日益嚴(yán)重。長(zhǎng)期處于強(qiáng)噪聲環(huán)境,會(huì)給人的生理、心理帶來(lái)很大危害,因此,噪聲污染、大氣污染和水污染一并被稱(chēng)為世界三大污染。為了降低噪聲的影響,需要設(shè)計(jì)出相應(yīng)的噪聲控制方案,而方案的設(shè)計(jì)依賴(lài)于準(zhǔn)確定位噪聲源的分布和估算其強(qiáng)度。近些年,基于聲傳感器陣列的噪聲源辨識(shí)測(cè)量應(yīng)用與研究正變得越來(lái)越廣泛[1-2]。
陣列信號(hào)處理算法主要是波束形成算法,包括將采集數(shù)據(jù)進(jìn)行延時(shí)相加的經(jīng)典算法[3]、具有較強(qiáng)點(diǎn)聲源分辨能力的逆向法[4]、能夠顯著提高聲源分辨率的反卷積算法[5],以及有效提高旁瓣抑制能力、減小虛假聲源干擾的算法[6]等。經(jīng)典算法由于其穩(wěn)定性和普適性,目前應(yīng)用最為普遍。然而,經(jīng)典算法不具備實(shí)時(shí)性,不能對(duì)運(yùn)動(dòng)或者旋轉(zhuǎn)聲源進(jìn)行定位,并且生成的圖像分辨率偏低,雖然可通過(guò)增大陣列直徑,增加陣列單元數(shù)來(lái)提高分辨率,但需要處理龐大的實(shí)驗(yàn)數(shù)據(jù)才能分離出信號(hào)源。隨著處理數(shù)據(jù)的增加,經(jīng)典算法表現(xiàn)出越來(lái)越多的局限性,比如:需要的數(shù)據(jù)存儲(chǔ)空間大,收斂速度慢等。此外,在將陣列技術(shù)推廣到運(yùn)動(dòng)聲源定位的過(guò)程中,需要對(duì)聲源到聲傳感器之間的傳遞函數(shù)進(jìn)行修正,采用修正后的傳遞函數(shù)對(duì)測(cè)量信號(hào)進(jìn)行重構(gòu),得到準(zhǔn)確測(cè)量結(jié)果[7]。但對(duì)于運(yùn)動(dòng)軌跡未知且運(yùn)動(dòng)軌跡復(fù)雜的聲源,處理起來(lái)有一定難度,而且在時(shí)域內(nèi)修正會(huì)付出較大計(jì)算代價(jià)。特別是在聲源運(yùn)動(dòng)速度較慢,多普勒效應(yīng)影響不大的情況下,修正后的結(jié)果與未修正的結(jié)果區(qū)別不大,一味進(jìn)行修正耗費(fèi)很大的計(jì)算量,結(jié)果改善卻不明顯。
為了解決經(jīng)典算法對(duì)整體測(cè)量數(shù)據(jù)的依賴(lài)和低速聲源在定位過(guò)程中遇到的問(wèn)題,本文提出了一種基于卡爾曼濾波器的算法,其基本思想來(lái)自信號(hào)處理領(lǐng)域的卡爾曼濾波器理論,并與陣列噪聲測(cè)量過(guò)程相結(jié)合,將整個(gè)噪聲檢測(cè)過(guò)程視為利用卡爾曼濾波器進(jìn)行時(shí)間和空間的濾波過(guò)程。關(guān)于濾波估計(jì)聲源狀態(tài)的思想,在文獻(xiàn)[8-9]中也有體現(xiàn)。本文應(yīng)用卡爾曼濾波器算法進(jìn)行了單極子成像、實(shí)時(shí)性能方面的數(shù)值模擬和實(shí)驗(yàn)驗(yàn)證,并將其結(jié)果與經(jīng)典算法進(jìn)行了比對(duì)。結(jié)果表明:對(duì)于固定聲源,卡爾曼濾波器算法收斂速度快,成像效果好;對(duì)于某些運(yùn)動(dòng)速度不快、運(yùn)動(dòng)軌跡復(fù)雜的聲源,不僅可以實(shí)現(xiàn)實(shí)時(shí)定位,而且計(jì)算量也較小。
1 經(jīng)典算法
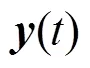
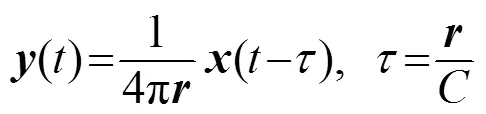
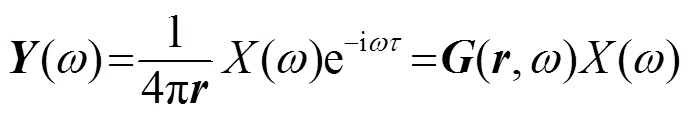
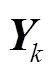
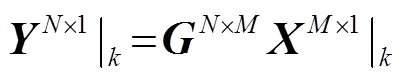
式(3)的解為:
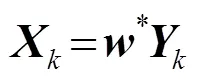
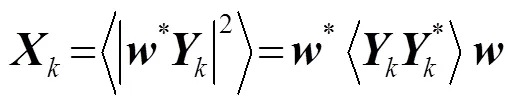
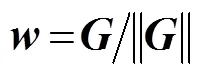
2 卡爾曼濾波器算法
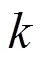
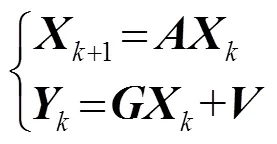
式(7)中的狀態(tài)更新矩陣A可通過(guò)圖1進(jìn)行說(shuō)明:由于聲源X為穩(wěn)態(tài)信號(hào),在狀態(tài)更新過(guò)程中,數(shù)據(jù)的頻譜信息也是穩(wěn)定的,因此A為單位矩陣[12]。為通道噪聲,假設(shè)其符合高斯白噪聲分布,均值為零,方差為。
對(duì)于系統(tǒng)方程(7)可設(shè)計(jì)卡爾曼濾波器進(jìn)行狀態(tài)估計(jì)。
狀態(tài)更新方程為
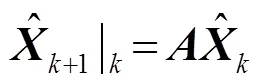
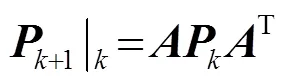
測(cè)量更新方程為
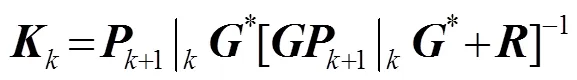
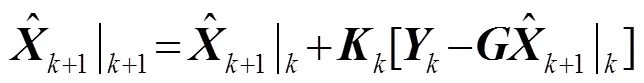
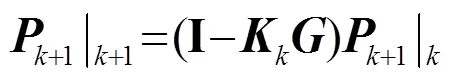
需要特別指出得是:式(7)~(12)并非僅能代表同窗數(shù)據(jù),可以根據(jù)測(cè)量需求進(jìn)行擴(kuò)展。例如:在去除背景噪聲過(guò)程中,可將式(7)中的狀態(tài)分別理解為背景噪聲、信號(hào)源,輸出理解為背景噪聲輸出、背景噪聲加信號(hào)源輸出。然后再按照式(8)~(12)迭代計(jì)算,去除背景噪聲,獲得聲源狀態(tài)。
3 仿真計(jì)算
3.1 點(diǎn)源成像
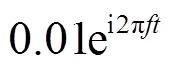
圖2(a)和圖2(b)分別顯示了經(jīng)典算法前20個(gè)數(shù)據(jù)塊和卡爾曼濾波器算法第10個(gè)數(shù)據(jù)塊結(jié)果,其中經(jīng)典算法未進(jìn)行譜交叉矩陣優(yōu)化。可以看到,在第10個(gè)數(shù)據(jù)塊時(shí),建立在對(duì)聲源狀態(tài)遞歸估計(jì)基礎(chǔ)上的卡爾曼濾波器算法就基本能夠達(dá)到未經(jīng)優(yōu)化的經(jīng)典算法前20個(gè)數(shù)據(jù)塊時(shí)的效果,收斂速度明顯高于經(jīng)典算法,而且主瓣動(dòng)態(tài)范圍較高,旁瓣抑制效果也較為明顯。
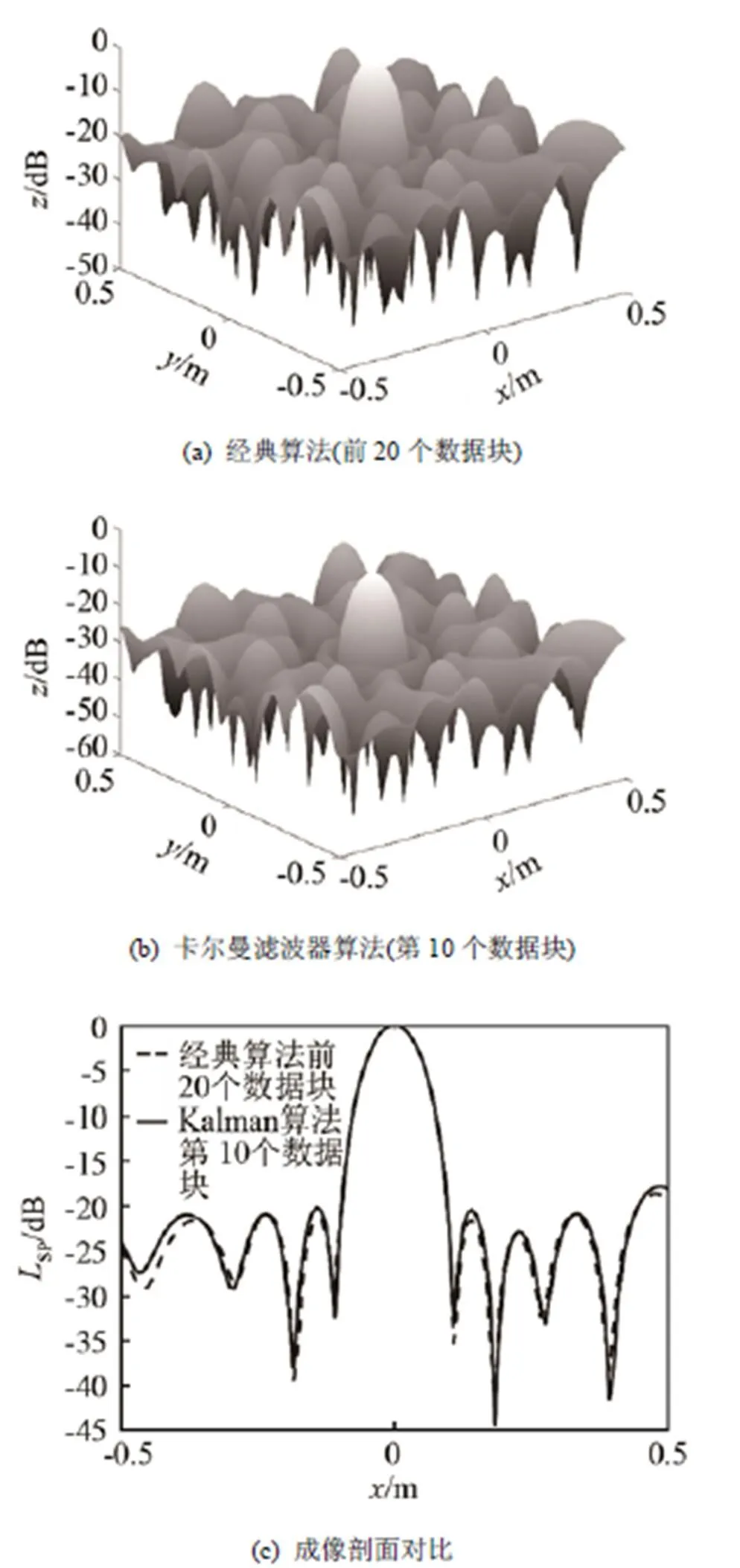
圖2 經(jīng)典算法和卡爾曼濾波器算法單極子成像對(duì)比
以上分析表明,卡爾曼濾波器算法在數(shù)據(jù)迭代過(guò)程中收斂更加迅速,可快速得出結(jié)果;另外,聲源波束形成動(dòng)態(tài)范圍大、準(zhǔn)確性高,成像結(jié)果令人滿(mǎn)意。
3.2 實(shí)時(shí)能力驗(yàn)證
圖3為運(yùn)動(dòng)聲源測(cè)量示意圖,邊長(zhǎng)為1 m的正方形陣列中包含56個(gè)聲傳感器,聲傳感器按照多臂螺旋線排列,在距離陣列0.7 m的平面上設(shè)置一個(gè)點(diǎn)聲源,點(diǎn)聲源按照正弦曲線運(yùn)動(dòng),運(yùn)動(dòng)軌跡與陣列平行,曲線的幅值為0.3 m,波長(zhǎng)為0.6 m,曲線中心位置與陣列中心線重合,其它參數(shù)與圖2相同。由于聲源距離陣列平面較近,運(yùn)動(dòng)速度不快,聲源運(yùn)動(dòng)所產(chǎn)生的零點(diǎn)誤差和漂移誤差很小,簡(jiǎn)單起見(jiàn),在成像結(jié)果中忽略多普勒效應(yīng)(對(duì)成像結(jié)果幾乎沒(méi)有影響),沒(méi)有對(duì)聲場(chǎng)進(jìn)行重建,在實(shí)際測(cè)量中要對(duì)測(cè)量精度和計(jì)算量進(jìn)行權(quán)衡而定。
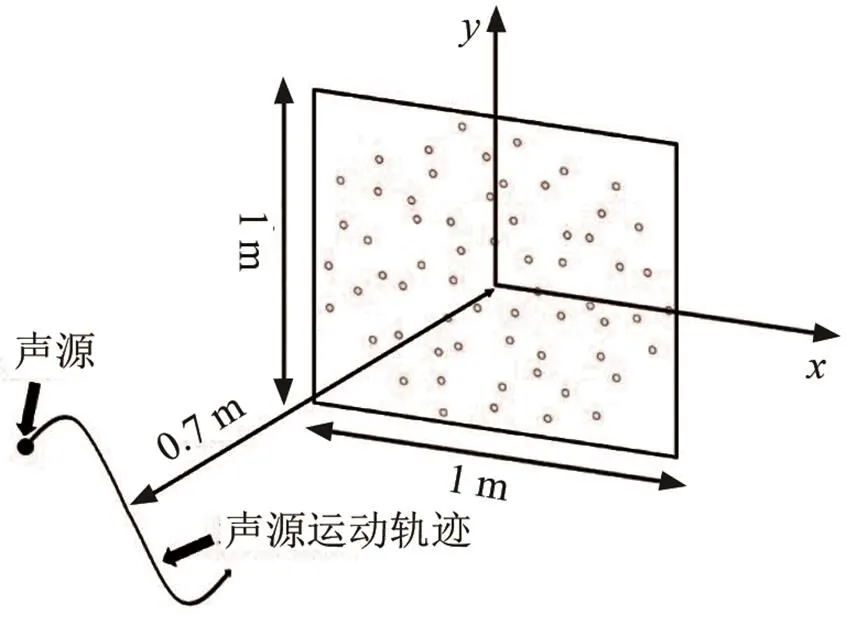
圖3 運(yùn)動(dòng)聲源測(cè)量示意圖
圖4為經(jīng)典算法對(duì)運(yùn)動(dòng)聲源的成像結(jié)果,動(dòng)態(tài)范圍顯示15 dB。其中,圖4(a)~4(d)分別為前25個(gè)、50個(gè)、75個(gè)和100個(gè)數(shù)據(jù)塊結(jié)果,圖中箭頭代表聲源的運(yùn)動(dòng)方向。可以看到,隨著聲源的運(yùn)動(dòng),整個(gè)軌跡上都出現(xiàn)了聲壓分布,沒(méi)有準(zhǔn)確定位到聲源的實(shí)時(shí)位置,其原因就在于經(jīng)典算法是基于統(tǒng)計(jì)-平均的思想,將采集到的數(shù)據(jù)離線統(tǒng)一處理,所有數(shù)據(jù)具有同等權(quán)重,這種處理方式不僅占用了運(yùn)算資源、浪費(fèi)了存儲(chǔ)空間,而且當(dāng)測(cè)量設(shè)備出現(xiàn)問(wèn)題時(shí)也不能及時(shí)發(fā)現(xiàn),只能再次進(jìn)行測(cè)量。因此,不具備實(shí)時(shí)性成為經(jīng)典算法的一個(gè)缺陷。
圖5為卡爾曼濾波器算法對(duì)運(yùn)動(dòng)聲源的成像結(jié)果,其中,圖5(a)~5(d)分別為第25個(gè)、50個(gè)、75個(gè)和100個(gè)數(shù)據(jù)塊結(jié)果。顯然,該算法實(shí)時(shí)、準(zhǔn)確定位了運(yùn)動(dòng)聲源的位置。在計(jì)算過(guò)程中采用的數(shù)據(jù)塊長(zhǎng)度為4 096,如果適當(dāng)縮短數(shù)據(jù)塊長(zhǎng)度,實(shí)時(shí)性能還會(huì)有所增加,數(shù)據(jù)塊長(zhǎng)度的選擇可根據(jù)待測(cè)聲源的運(yùn)動(dòng)速度進(jìn)行調(diào)節(jié)。對(duì)數(shù)據(jù)塊進(jìn)行迭代處理,使得卡爾曼濾波器算法計(jì)算量較小,對(duì)運(yùn)算資源和存儲(chǔ)空間的占用也較低,能夠及時(shí)發(fā)現(xiàn)在測(cè)量過(guò)程中存在的問(wèn)題,最主要的是這種算法具備了實(shí)時(shí)性,能夠準(zhǔn)確定位運(yùn)動(dòng)聲源的位置。
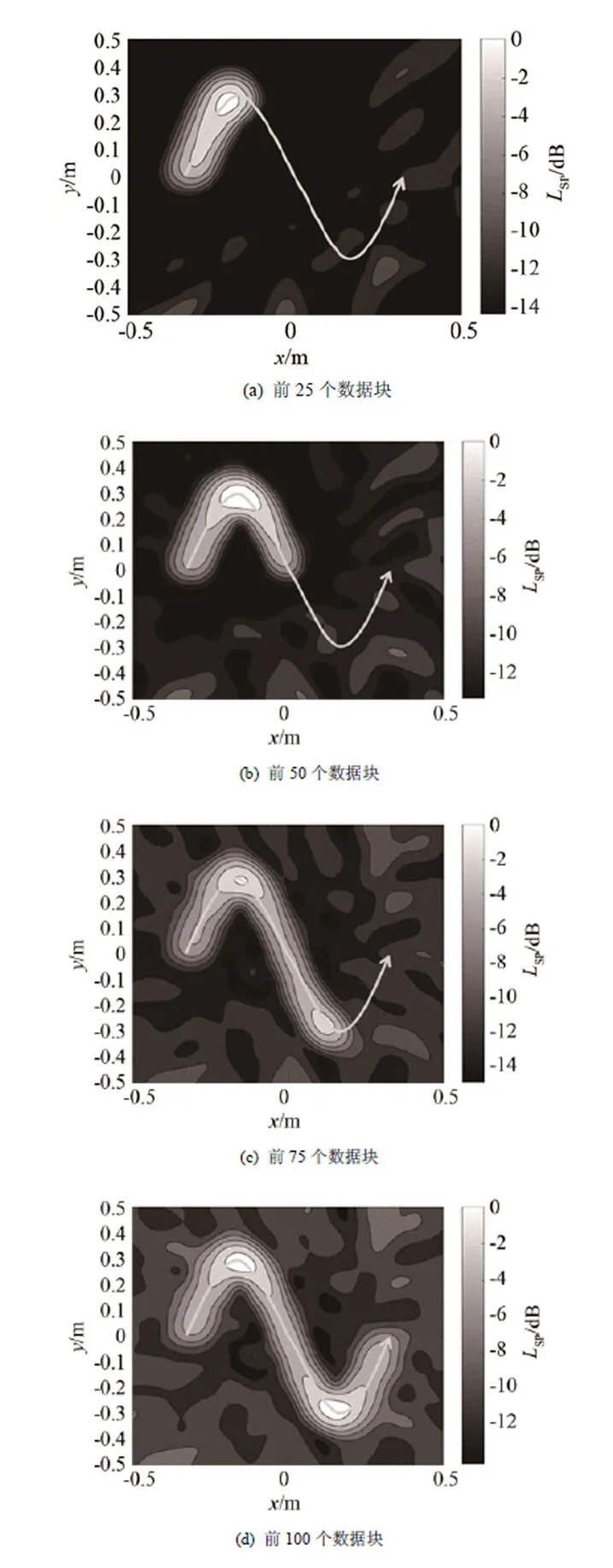
圖4 經(jīng)典算法運(yùn)動(dòng)聲源成像
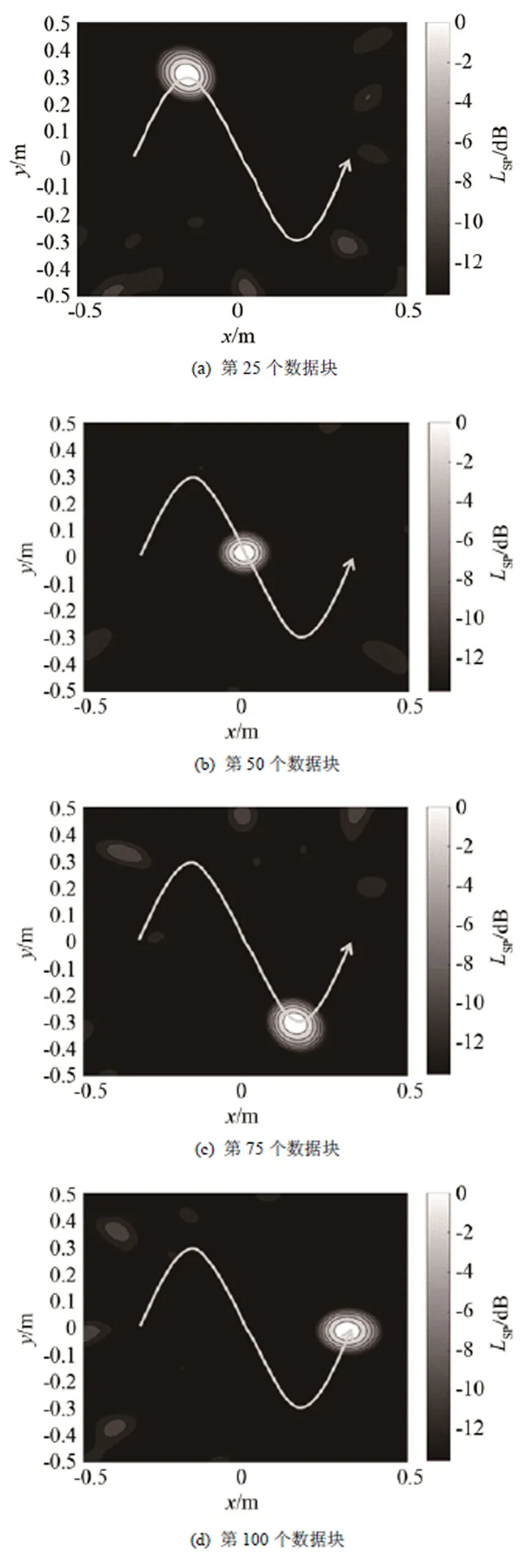
圖5 卡爾曼濾波器算法運(yùn)動(dòng)聲源成像
4 實(shí)驗(yàn)驗(yàn)證
為了驗(yàn)證卡爾曼濾波器算法的準(zhǔn)確性,在實(shí)驗(yàn)室內(nèi)進(jìn)行了如圖6所示的雙點(diǎn)聲源定位實(shí)驗(yàn),圖中兩個(gè)小音箱模擬單極子聲源,頻率均為3 kHz,距離陣列平面0.5 m,陣列含有56個(gè)通道,按照多臂螺旋線排列,采樣頻率48 kHz,數(shù)據(jù)塊長(zhǎng)度為4 096。
圖7和圖8分別展示了經(jīng)典算法和卡爾曼濾波器算法對(duì)于雙點(diǎn)聲源成像的結(jié)果,可以看到在第1個(gè)數(shù)據(jù)塊時(shí),經(jīng)典算法結(jié)果與卡爾曼濾波器算法結(jié)果基本沒(méi)有差別,但隨著處理數(shù)據(jù)塊的增加,卡爾曼濾波器算法收斂更快,到第10個(gè)數(shù)據(jù)塊時(shí),其結(jié)果已經(jīng)優(yōu)于了經(jīng)典算法,原因就在于卡爾曼濾波器對(duì)新信息的權(quán)重更大,在對(duì)聲源狀態(tài)進(jìn)行估計(jì)時(shí),將更快速地接近于真實(shí)值。

圖6 雙點(diǎn)源陣列成像實(shí)驗(yàn)
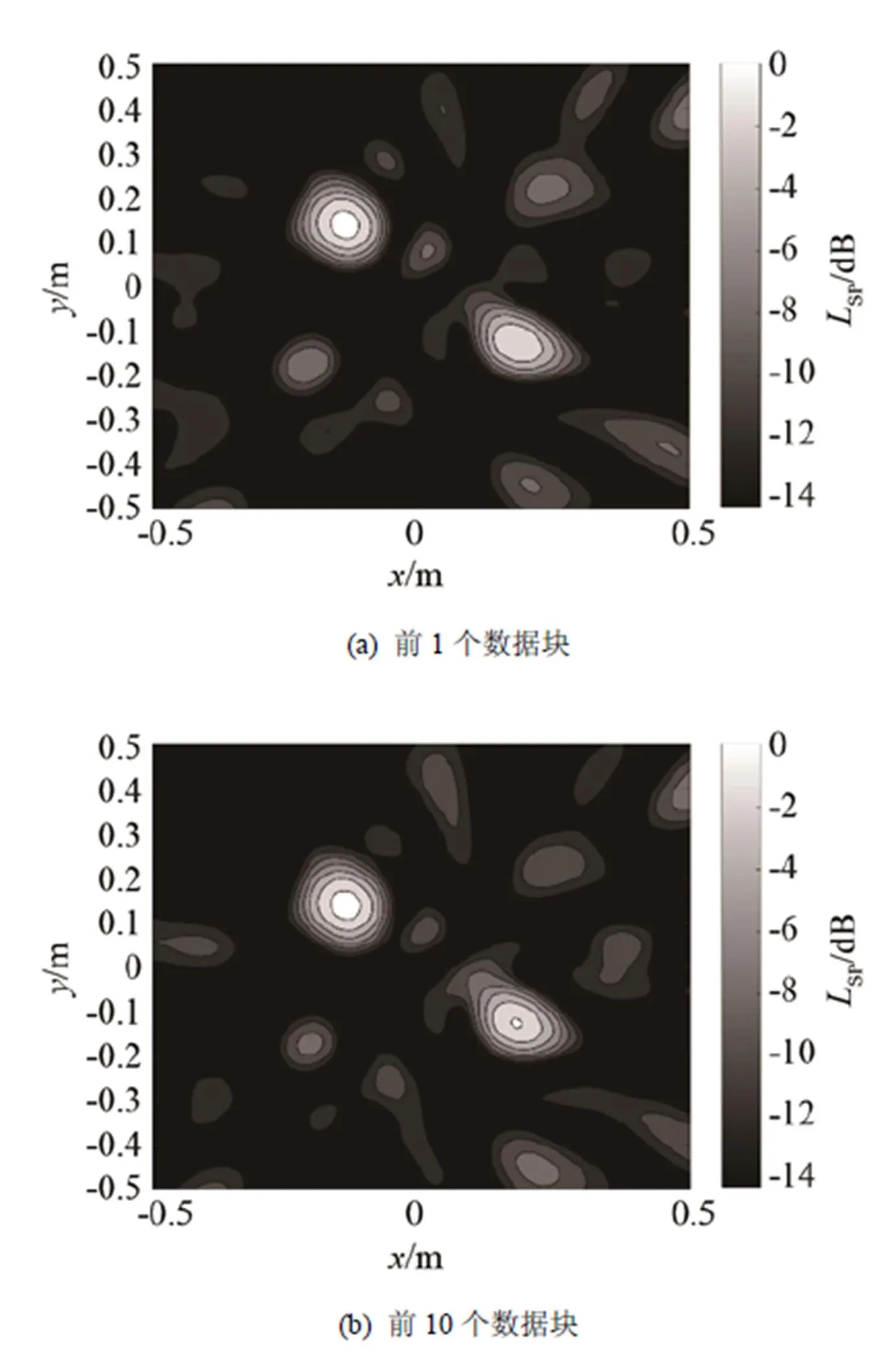
圖7 經(jīng)典算法計(jì)算雙點(diǎn)聲源
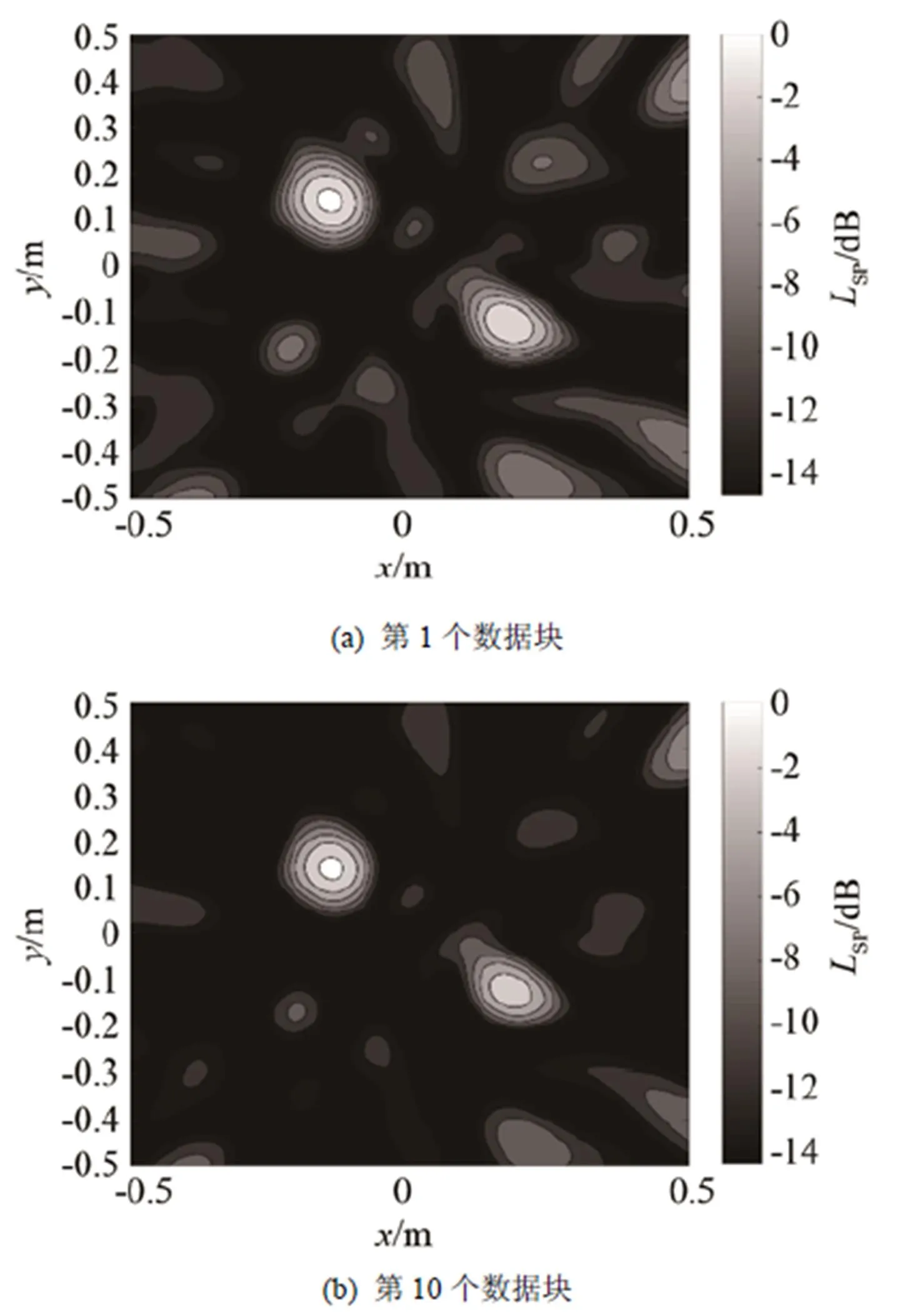
圖8 卡爾曼濾波器算法計(jì)算雙點(diǎn)聲源
5 結(jié)論
使用陣列進(jìn)行氣動(dòng)聲源測(cè)量時(shí),要根據(jù)測(cè)量對(duì)象和成像要求選擇不同的算法。本文從狀態(tài)估計(jì)角度提出了基于卡爾曼濾波器的算法,在頻域內(nèi)對(duì)陣列采集數(shù)據(jù)進(jìn)行迭代處理,估計(jì)系統(tǒng)狀態(tài)。仿真結(jié)果表明,該方法不僅能夠準(zhǔn)確定位固定聲源,而且能夠跟蹤某些運(yùn)動(dòng)聲源,實(shí)現(xiàn)實(shí)時(shí)定位。通過(guò)分析可以得到以下結(jié)論:
(1) 對(duì)于固定聲源,經(jīng)典算法對(duì)所有數(shù)據(jù)進(jìn)行統(tǒng)計(jì)-平均,結(jié)果較為穩(wěn)定;對(duì)于狀態(tài)變化的聲源,采用基于卡爾曼濾波器的算法,不僅能夠消除測(cè)量誤差,而且能夠?qū)崟r(shí)顯示聲源狀態(tài)。
(2) 卡爾曼濾波器算法具有強(qiáng)大的實(shí)時(shí)數(shù)據(jù)處理能力,適合于某些運(yùn)動(dòng)軌跡較為復(fù)雜、運(yùn)動(dòng)速度慢、離陣列平面近的聲源,收斂速度快,節(jié)約了運(yùn)算和存儲(chǔ)成本,聲源成像動(dòng)態(tài)范圍大。
(3) 在縮短數(shù)據(jù)塊長(zhǎng)度、提高實(shí)時(shí)性的過(guò)程中,如何提高卡爾曼濾波器算法分辨率需要進(jìn)一步研究;另外,卡爾曼濾波器算法是在頻域內(nèi)進(jìn)行的迭代運(yùn)算,如何將算法發(fā)展到時(shí)域,加入多普勒效應(yīng)修正也是今后研究的重點(diǎn)。
[1] MOREAU D J, DOOLAN C J, ALEXANDER W N, et al. Wall-mounted finite airfoil-noise production and prediction[J]. Aiaa Journal, 2016, 54(5): 1637-1651.
[2] 季建朝, 王明新, 周永清. 閉口風(fēng)洞聲學(xué)測(cè)量中的陣列設(shè)計(jì)[J]. 聲學(xué)技術(shù), 2018, 37(2): 99~104.
JI Jianchao, WANG Mingxin, ZHOU Yongqing. Array design for acoustic measurement in closed wind tunnel[J]. Technical Acoustics, 2018, 37(2): 99-104.
[3] VEEN B D V, BUCKLEY K M. Buckley. Beamforming: a versatile approach to spatial filtering[J]. IEEE ASSP Mag, 1988, 5(2): 4-24.
[4] LI S, XU Z, HE Y, et al. Generalized inverse beamforming via elastic net regularization[J]. Chinese Journal of Scientific Instrument, 2015, 36(5): 1170-1176.
[5] 楊洋, 褚志剛, 江洪,等. 反卷積DAMAS2波束形成聲源識(shí)別研究[J]. 儀器儀表學(xué)報(bào), 2013, 34(8): 1779-1786.
YANG Yang, CHU Zhigang, JIANG Hong, et al. Research on DAMAS2 beamforming sound source identification[J]. Chinese Journal of Scientific Instrument, 2013, 34(8): 1779-1786.
[6] 李征初, 李勇, 陳正武, 等. CLEAN-SC算法在風(fēng)洞聲源定位與識(shí)別中的應(yīng)用研究[J]. 實(shí)驗(yàn)流體力學(xué), 2016, 30(3): 104-109.
LI Zhengchu, LI Yong, CHEN Zhengwu, et al. Noise identification and localization in wind tunnel using CLEAN-SC algorithm[J]. Journal of Experiments in Fluid Mechanics, 2016, 30(3): 104-109.
[7] 張杰. 基于麥克風(fēng)平面陣列的運(yùn)動(dòng)噪聲源定位及算法研究[D]. 杭州: 中國(guó)計(jì)量學(xué)院, 2014.
ZHANG Jie. Research on Moving Noise Source Localization Methods Based on Plane Microphone Array[D]. Hangzhou: China Jiliang University, 2014.
[8] HUANG X. Real-time algorithm for acoustic imaging with a microphone array[J]. J. Acoust. Soc. Am., 2009, 125(5): 190-195.
[9] HUANG X, VINOGRADOV I, BAI L, et al. Observer for phased microphone array signal processing with nonlinear output[J]. Aiaa Journal, 2010, 48(11): 2702-2705.
[10] 季建朝, 張宇, 王明新. 聲傳感器陣列風(fēng)洞測(cè)量結(jié)果優(yōu)化[J]. 清華大學(xué)學(xué)報(bào)(自然科學(xué)版), 2018, 58(1): 94-100. JI Jianchao, ZHANG Yu, WANG Mingxin. Optimization of acoustic sensor arrays for wind tunnel measurements[J]. Journal of Tsinghua University(Science and Technology), 2018, 58(1): 94-100.
[11] MUELLER T J. Aeroacoustic measurements[M]. Berlin Heidelberg: Springer,2002: 66-67.
[12] PEEBLES P Z. Probability, random variables, and random signal principles[M]. New york: McGraw-Hill, 1987.
[13] BURNSIDE N, JAEGER S, REINERO B, et al. Array design and performance for a large scale airframe noise study[C]//8th AIAA/CEAS Aeroacoustics Conference & Exhibit. 2002: 2576.
[14] JAEGER S, HORNE W, ALLEN C. Effect of surface treatment on array microphone self-noise[C]//6th Aeroacoustics Conference and Exhibit. 2000: 1937.
Kalman filter-based algorithm for acoustic array measurement
JI Jian-chao1,2, ZHANG Yu2, ZHAO Zi-long2, XIA Lu2
(1. College of Aeronautics and Astronautics, Tsinghua University, Beijing 100084, China; 2. Army Aviation Institute, Beijing 101123, China)
The conventional beamforming (CB) is the most popular signal processing technique for noise identification using acoustic sensor arrays. However, CB does not have real-time performance and takes up a lot of storage space, the calculation speed is slow. A new approach called Kalman filter based beamforming method is introduced in this paper, which has a recursive form similar to Kalman filter in signal processing field. The data collected by acoustic array are processed iteratively in frequency domain, it can not only detect various problems in the wind tunnel survey, but also eliminate the errors caused by the test environment in real time. The simulation results show that the algorithm converges faster than the CB algorithm, the imaging results is very good, more importantly, it can accurately locate some low speed moving sound sources. This algorithm runs in real-time, so it is an attractive new algorithm for the real-time localization of wind tunnel sound source.
aeroacoustics; array processing; beamforming; recursive functions
V211.71
A
1000-3630(2018)-06-0601-06
10.16300/j.cnki.1000-3630.2018.06.016
2017-11-27;
2018-02-05
國(guó)家自然科學(xué)基金(11402305)資助項(xiàng)目。
季建朝(1981-), 男, 河北保定人, 博士, 講師, 研究方向?yàn)槁晫W(xué)測(cè)量、聲學(xué)控制。
季建朝, E-mail: jianchao_ji@163.com

