不依賴于子波的聲波多尺度全波形反演方法

周敏，武杰

?

不依賴于子波的聲波多尺度全波形反演方法

周敏1，武杰2

(1. 中國科學技術大學近代物理系，安徽合肥 230026；2.中國科學技術大學核探測技術與核電子學國家重點實驗室，安徽合肥 230026)

伴隨著油氣勘探目標復雜性的日益增加，對速度場建模和成像方法都提出了更高的要求。聲波介質下的全波形反演方法是現階段精度最高的速度場建模方法，在復雜介質速度場建模方面具有一定的應用前景。然而，傳統的波形反演方法對地震子波的準確性具有較高的依賴性，并且在地震數據主頻較高的情況下難以得到有效的反演結果。為此，基于聲波方程，通過修改維納濾波器，通過利用參考道構建濾波器，提出了一種不依賴于子波的全波形反演方法，能夠有效避免波形反演對子波的依賴性。由于濾波器目標子波選取較為自由，該方法可以與多尺度反演策略有機結合，實現頻率由低到高的遞進反演，能夠進一步提高反演的穩定性。理論分析和模型試算證明，采用不依賴于子波的多尺度反演方法能夠有效避免子波提取問題，在子波錯誤的情況下可以得到準確的反演結果，并且能夠在保證反演穩定性的基礎上提高反演精度，反演效果優于傳統的波形反演方法。

速度場建模；全波形反演；不依賴于子波；多尺度反演

0 引言

高精度的速度場建模是針對復雜介質成像處理和儲層預測的關鍵所在。現階段常規地震數據處理的流程是：首先利用走時信息，通過速度分析和層析等建立背景速度場，然后通過偏移或者最小二乘偏移對地下介質進行成像。由于僅僅利用走時信息建立的速度場精度有限，難以滿足高精度成像的需求。近年來被逐漸采用的地震數據反演方法、全波形反演方法在理論上能夠充分利用地震數據中不同類型波的走時、振幅等信息，通過數據匹配來獲得半波長級的速度建模精度[1-2]，因此在復雜介質的地震數據處理中具有更好的應用前景。伴隨地震數據采集質量以及計算機計算能力的提升，全波形反演方法被廣泛地應用于不同的數據和模型域以及不同的地層介質[3-6]。

然而，全波形反演是一個極強的非線性問題，地震數據中子波準確與否、數據的頻率成分等直接決定了速度場建模的精度[7-10]。傳統的全波形反演方法將目標泛函直接定義為觀測數據與模擬數據之間殘差的二范數，不對數據進行預處理[2]。因此，在反演過程中往往會出現地震子波不匹配、地震數據頻率過高導致觀測數據與模擬數據不能有效匹配等問題。為了避免子波不準確對全波形反演精度和穩定性的影響，不同學者發展了不依賴于子波的全波形反演方法[11-12]。不依賴于子波的全波形反演方法可以分為在時間域和頻率域反演兩大類，由于在時間域反演不需要頻率域中的除法運算，因此具有更高的穩定性[13]。將時間域不依賴于子波的全波形反演方法與多炮反演策略相結合，得到了較好的反演效果。針對地震數據主頻較高導致波形反演不穩定的問題，現階段廣泛采用多尺度反演策略，通過對地震數據在時間域或者頻率域進行濾波，實現對地震數據由低頻到高頻的遞進反演，能夠在保證反演穩定性的基礎上提高反演精度[14-15]。結合優化的頻率選擇策略[16]，多尺度反演的計算效率能夠有效提升，并且時間域的多尺度反演方法相對頻率域效率更高。

本文在前人工作的基礎上，針對實際地震數據中子波難以提取、地震數據主頻較高的問題，利用維納濾波器提出了一種聲介質不依賴于子波的多尺度全波形反演方法，一方面避免子波不準確問題對全波形反演的影響，另一方面利用多尺度反演思想，在保證反演穩定性的基礎上提高反演精度。本文首先介紹全波形反演的基本理論，在此基礎上給出基于維納濾波器的不依賴于子波的多尺度反演方法；然后通過模型試算證明本文中方法的有效性和正確性；最后詳細分析了本文中方法的優缺點。

1 理論方法

1.1 全波形反演

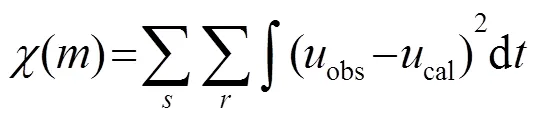
目標泛函關于模型參數的梯度項可以通過伴隨狀態法[17-18]求得：

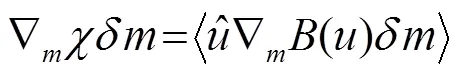
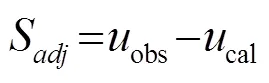
全波形反演通過對模型參數的迭代更新求得最優解，其迭代公式可以表示為

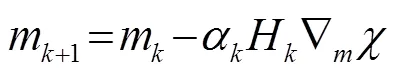
1.2 時間域多尺度全波形反演

傳統的全波形反演方法直接利用全頻帶的地震數據，因此在地震數據主頻較高或者初始模型不準確的情況下容易陷入局部極小。為了提高全波形反演方法的穩定性，Boonyasiriwate等[15]利用維納濾波器提出了一種時間域的多尺度全波形反演方法。維納濾波器的特征在于其可以將原始信號轉化為與目標信號十分相似的形式，其在頻率域的表示形式為

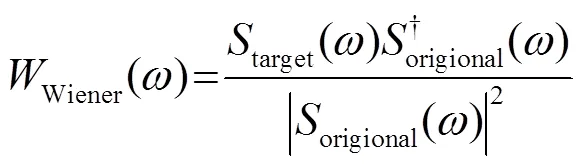
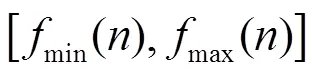
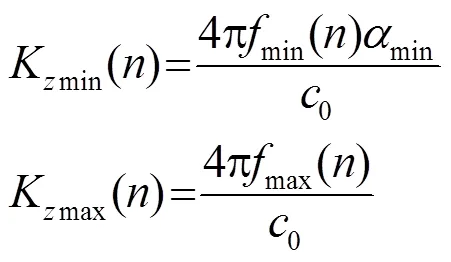
則相應的頻率選擇策略為

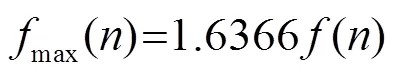
1.3 不依賴于子波的多尺度反演方法

然而，值得注意的是上述時間域的多尺度反演方法必須是以已知地震子波為前提的，在地震子波未知的情況下難以適用。因此必須要采用復雜的子波估計方法來獲取子波形式[22-23]。為了避免復雜的子波估計過程，本文根據卷積模型對原始的維納濾波器進行修改。從地震數據中選擇一路參考道，參考道在頻率域可以表示為子波與反射系數的卷積：

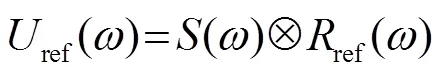
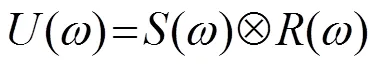
其中，為頻率域的反射系數。利用參考道來構建的維納濾波器可以表示為

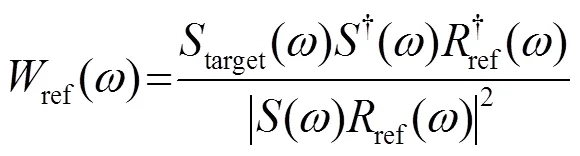
利用式(12)所示的維納濾波器對地震數據進行濾波可以得到：

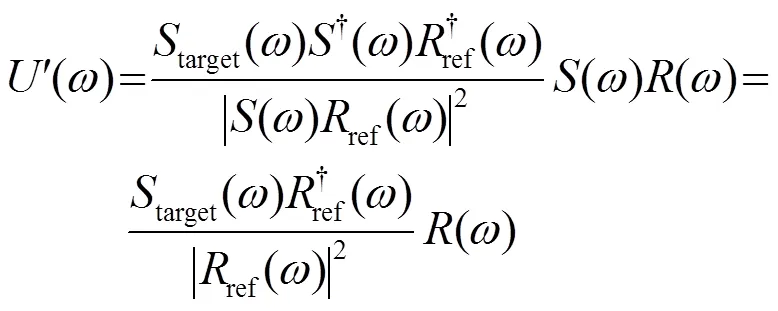
由式(10)可見，地震子波項在濾波后的數據被消除。對觀測數據和正演模擬數據分別構建維納濾波器，并對數據進行維納濾波處理，其分別可以表示為：

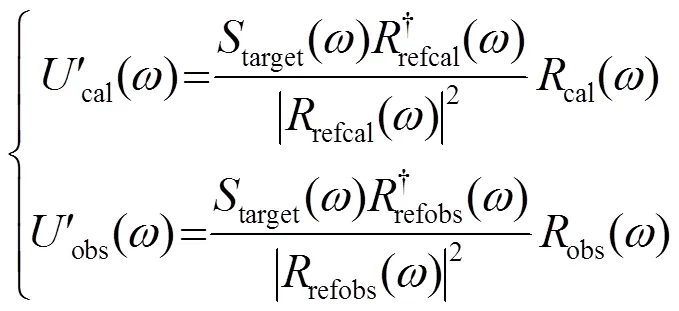
其中，下標帶有cal和obs的變量分別表示正演模擬數據和觀測數據。

目標泛函被定義為濾波后的正演模擬數據和觀測數據的殘差的二范數：

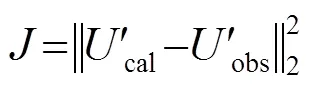
可見地震子波項在新的目標泛函中被消除。利用伴隨狀態法[17-18]，相應的伴隨震源可以表示為

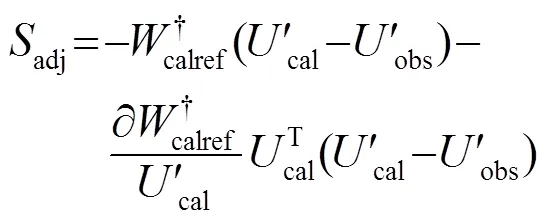
與傳統的基于維納濾波器的多尺度反演方法相似[15]，由于目標子波的選取具有一定的自由性，因此可以直接實現由低頻到高頻的多尺度反演方法，即將反演分為幾個階段，在反演的早期采用低頻子波作為目標子波，主要保證波形反演避免局部極小，反演地下的低波數大尺度結構；在反演后期采用高頻子波，提高全波形反演的反演精度，主要反演高波數組分。因此可以實現在保證反演穩定性的基礎上提高反演精度。

對于參考道的選取，主要有采用單一地震記錄和采用所有地震記錄的疊加作為參考道兩種。Choi 等[11]在基于卷積的不依賴于子波的聲波全波形反演方法中指出，利用全部地震記錄的累加作為參考道的反演效果要優于采用單一地震道作為參考道。其主要原因在于Choi等[11]將不依賴于子波的策略應用于多炮混疊數據反演中，采用多道疊加能夠在一定程度上壓制隨機噪聲和減少多炮混疊數據產生的交叉噪聲問題。而本文方法在本質上是基于反褶積的，將不依賴于子波的策略應用于單炮數據反演中，故不存在交叉噪聲問題；除此之外，多道數據疊加使得參考道的反射系數形式更為復雜，構造的濾波器容易出現不穩定現象，并且由此獲得的伴隨震源的形式也更為復雜(見式(16))，所以本文采用單一地震記錄作為參考道。必須指出的是，由于地震波在傳播過程中可能出現衰減或子波畸變等現象，因此距離震源遠的地震道相比于近的地震道要更加復雜，在選取地震道時應該優先選取距離震源近的地震道。

2 模型試算

為了驗證本文方法的正確性和有效性，將文中的方法應用于模型進行反演測試。用時間2階、空間8階的有限差分聲波介質正演模擬以及完全匹配層(Perfect Match Layer, PML)邊界條件做正演模擬[24-25]，模型的縱橫向網格均為10 m。對于觀測數據，采用主頻為15 Hz的高斯子波，在反演過程中假設子波是主頻為15 Hz的雷克子波。不同子波的形態如圖1所示。由于觀測數據和反演過程中采用的子波形態不同，所以會導致波形反演不穩定。

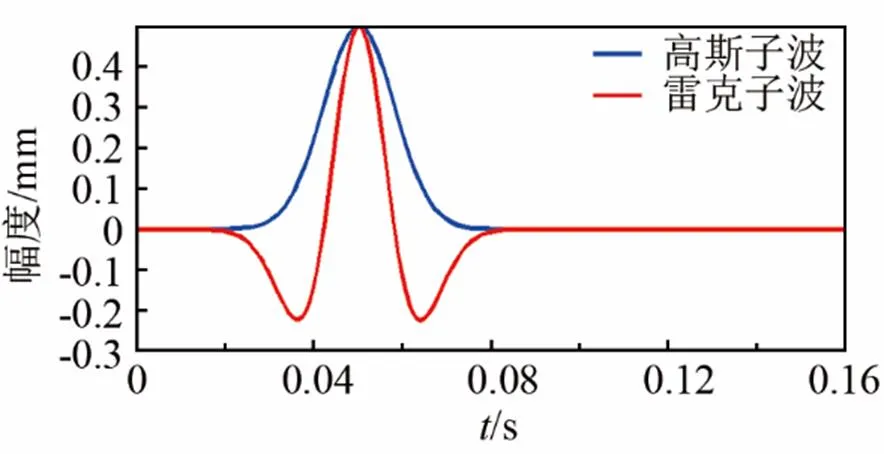
圖1 高斯子波和雷克子波的形態對比

2.1 層狀模型測試

將本文中方法應用于如圖2(a)所示的層狀真實模型中，其特征為多個速度相同的層狀構造相互疊合，速度差異較小，并且存在一定的高陡位置，主要測試聲介質全波形反演在存在多個速度差異較小和存在高陡構造情況下的反演能力。采用與上例中相同的觀測系統，采用的初始模型由對真實模型進行平滑得到，如圖2(b)所示。圖3為利用聲波波動方程對真實模型進行正演所得到的波場快照，可見在除了直達波之外，由于速度界面的存在，產生了較強的反射聲波。眾多的反射界面導致波場較為復雜，因此波形反演的難度也相對較大。

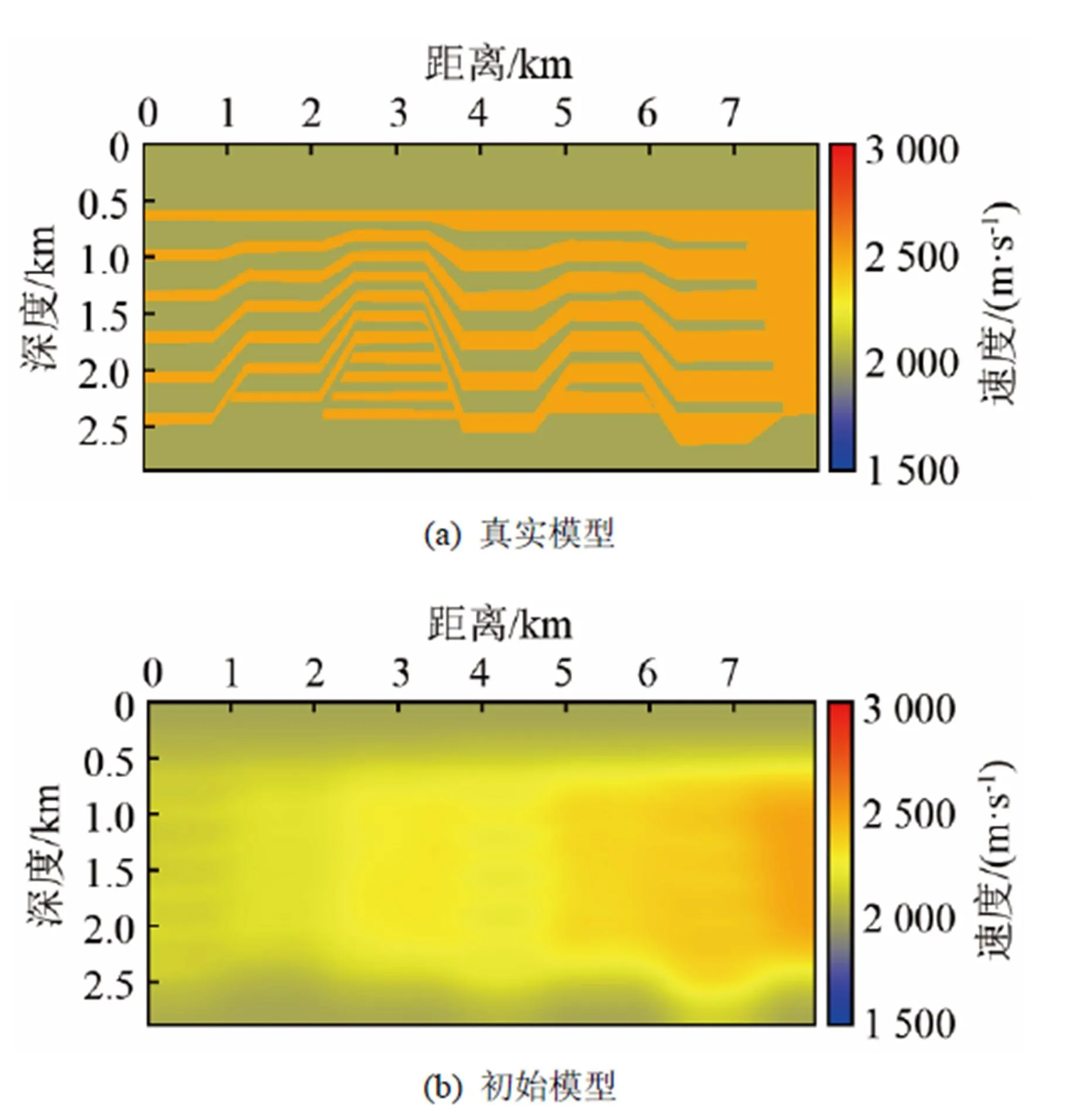
圖2 層狀模型的真實模型和初始模型

圖3 0.8 s時的波場快照

圖4為在子波錯誤的情況下采用傳統全波形反演方法得到的反演結果。由圖4可見，一方面由于初始模型與真實模型相差較遠，另一方面由于反演過程中采用的子波與真實子波不同，反演結果并沒有給出有效的地層信息，在模型的淺層存在較強的反演噪聲，并且嚴重影響了深層的反演結果。

圖5為采用本文中不依賴于子波的多尺度反演方法的反演結果，采用的目標子波是主頻為15 Hz的雷克子波，由于地震數據主頻較高，并且初始模型不夠準確，反演結果與真實模型相差較遠，并且在淺層存在明顯的反演噪聲。但是相比較于子波不準確的情況，反演結果有了一定的提升，一些深層的速度層位信息得以解釋。

為了進一步提高反演效果，采用多尺度的反演策略，目標子波為雷克子波，其主頻由3 Hz變化至15 Hz，變化步長為2 Hz，所選用的頻率間隔要明顯小于理論計算值(理論計算所得的反演頻率組分別為：6 Hz、15 Hz)，目的是為了避免在波形反演過程中因波數不連續而引起反演異常[21]。每個階段的迭代次數為5次，最后一個階段持續迭代直至模型總迭代次數為100次。最終的反演結果如圖6所示。可見相比較于未采用多尺度策略的反演結果，反演精度有了明確提升，淺層的速度層位被準確刻畫，深層的速度層位反演效果也有了明顯提升，能夠有效反演部分高陡界面。然而，整體而言，深層的反演效果要低于淺層的反演效果，這一方面是因為由于擴散效應，地震波在深層的能量較弱，另一方面是因為地震波在薄互層中的多次傳播產生的多次波引起的能量衰減。除此之外，一些深層的高陡界面的反演效果不夠理想，主要是由觀測系統的偏移距有限導致的。

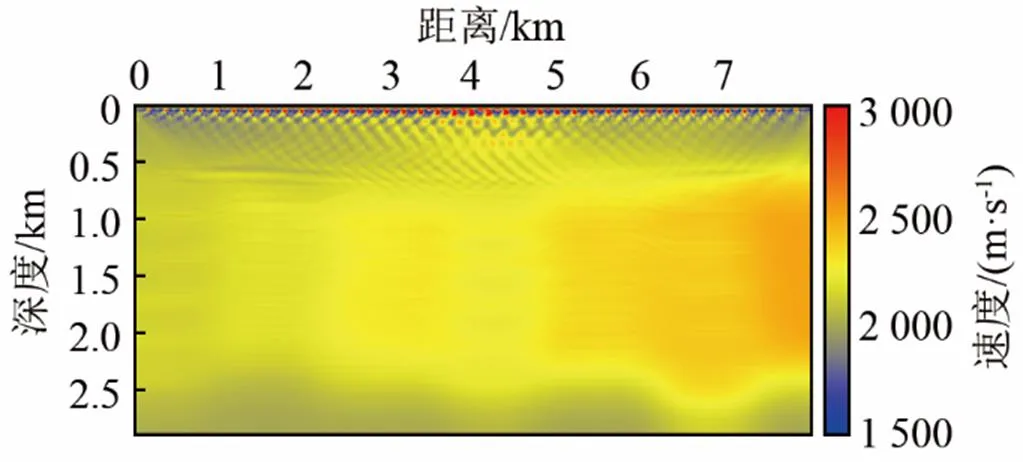
圖4 層狀模型的傳統全波形反演結果

圖5 不采用多尺度策略的不依賴于子波的全波形反演結果(層狀模型)

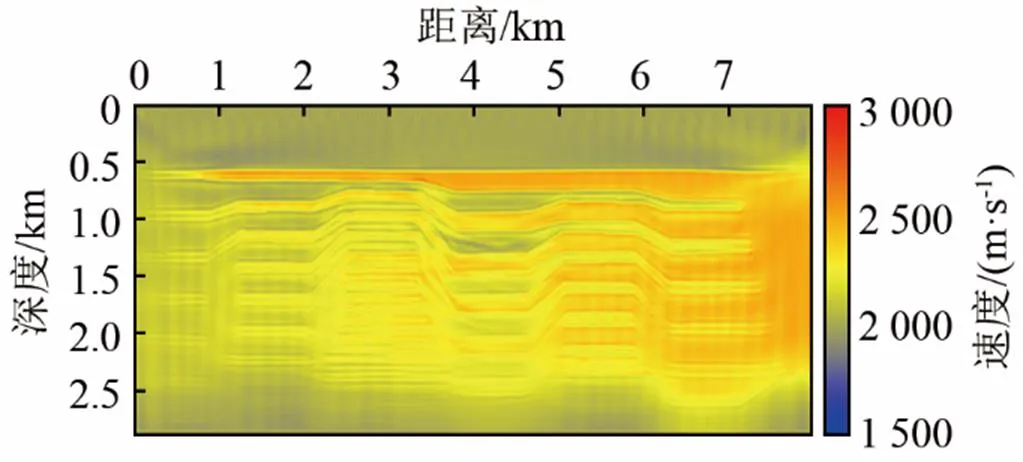
圖6 不依賴于子波的多尺度反演結果(層狀模型)

2.2 復雜模型測試

為了測試本文方法對復雜模型的適用性，將本文方法應用于如圖7(a)所示的復雜模型中，模型縱橫向網格均為10 m，所采用的觀測系統與上例相同，初始模型由對真實模型平滑生成，如圖7(b)所示，淺層水層速度假定為已知。

首先采用傳統的全波形反演方法進行反演測試，其反演結果如圖8所示，可見與前面兩例相似，由于子波不準確，在模型的淺層存在明顯的反演噪聲。子波不同導致的直達波殘差是導致淺層的高速反演噪聲的主要原因；模型的深層沒有任何有效的速度更新，僅僅存在一些高波數的反演噪聲，說明在子波不準確的情況下全波形反演難以提供有效的速度場反演。

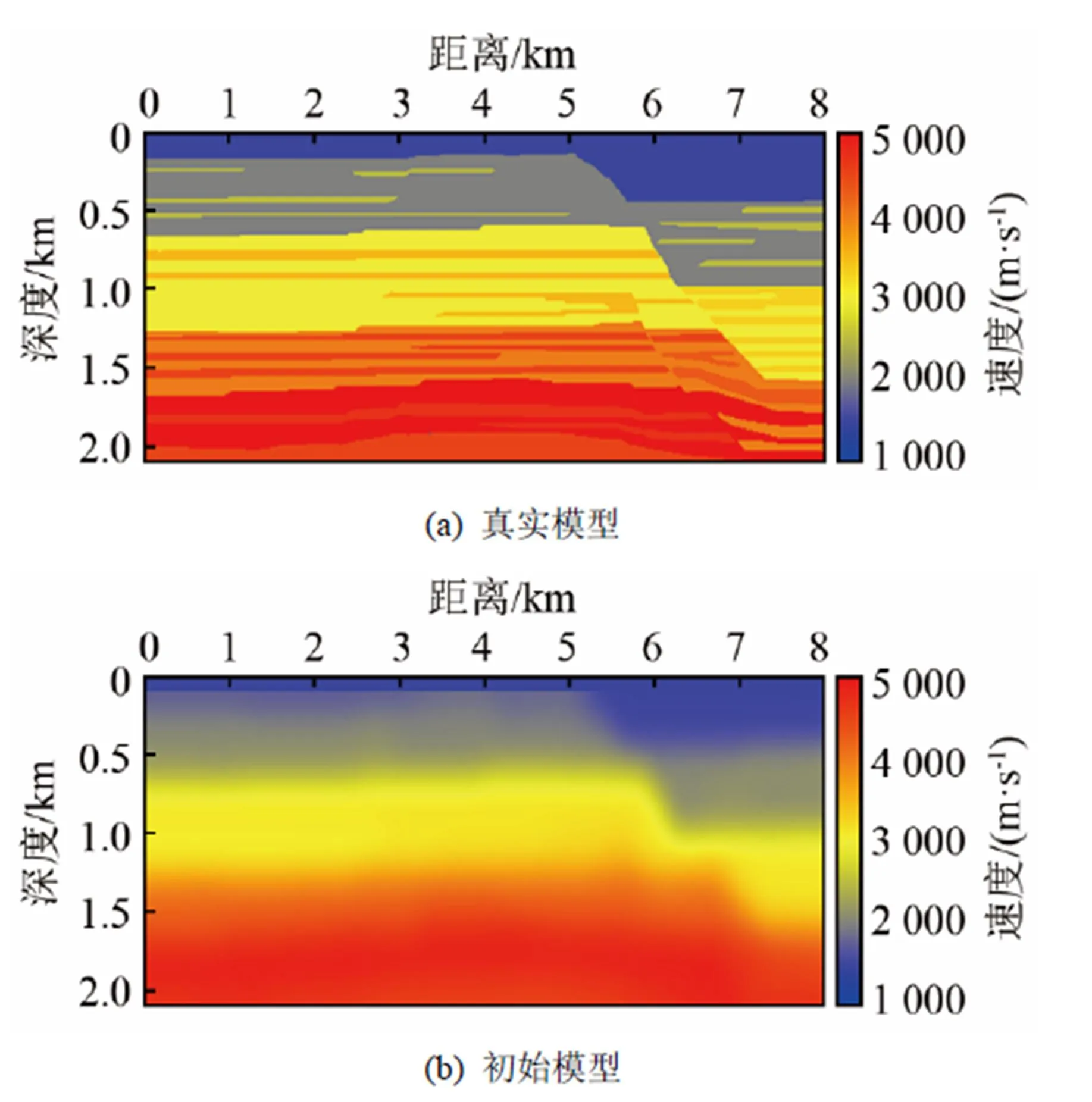
圖7 復雜模型的真實模型和初始模型

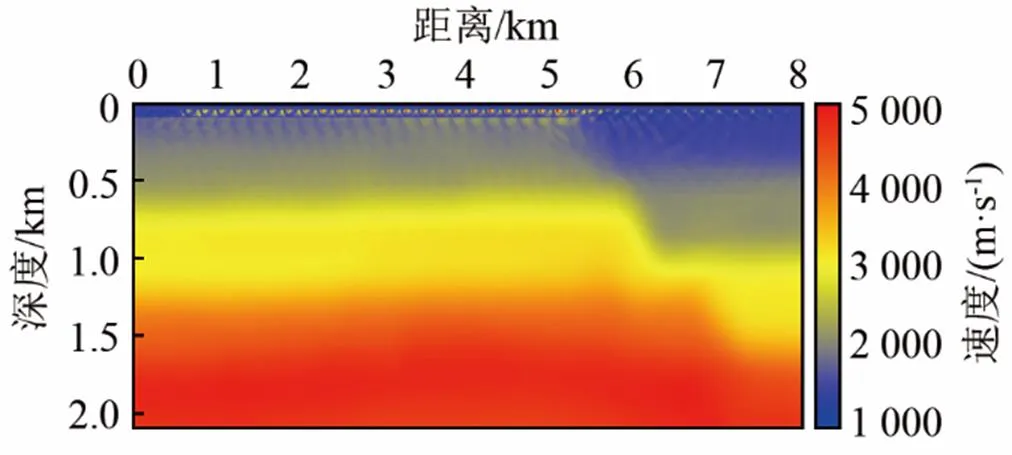
圖8 復雜模型的傳統全波形反演結果

圖9為采用本文中不依賴于子波的全波形反演方法的反演結果，目標子波是主頻為15 Hz的雷克子波。由圖9可見，相比較于常規的全波形反演方法，本文中方法能夠有效消除由于子波不準確引起的淺層反演噪聲，反演結果中不存在高速噪聲。除此之外，模型的淺層存在的一些薄層也被部分刻畫。但是整體而言，由于波形反演采用的數據主頻較高，并且初始模型與真實模型相差較大，因此在不采用多尺度的情況下波形反演對模型的恢復能力有限。

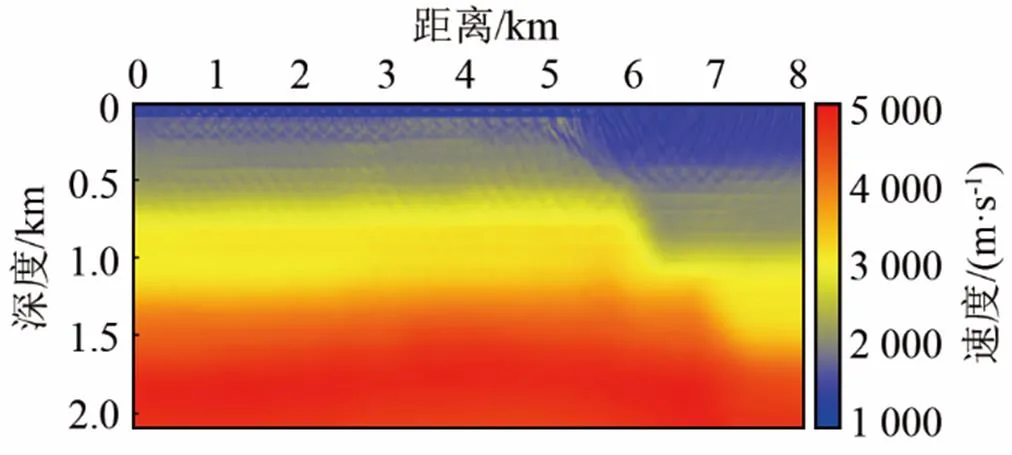
圖9 不采用多尺度策略的不依賴于子波的全波形反演結果(復雜模型)

為了進一步提升反演效果，采用多尺度的反演策略，目標子波為雷克子波，其主頻由7 Hz變化到15 Hz，子波主頻變化步長為2 Hz，每個階段迭代10次，最后一次持續迭代直至總的迭代次數達到100次。其最終的反演結果如圖10所示，由圖10可見，一方面相比于傳統的波形反演，淺層的高速反演噪聲被明顯消除；模型淺層存在的薄層也被準確刻畫，層位位置和厚度比較準確。除此之外，模型中深層的反演效果有了明顯提升，中層的薄層也被有效反演，反演結果與真實模型十分接近。然而，在模型深層的速度更新量有效，其主要原因是由于擴散效應，模型深層地震波的能量較弱。右側斷層位置存在一定的反演噪聲，其主要原因為觀測數據的偏移距較小，接收到的斷層位置的反射波能量較弱，因此反演效果不夠理想。但是總體而言，本文中多尺度不依賴于子波的反演方法得到的反演效果要明顯優于傳統方法，驗證了本文中方法的有效性。

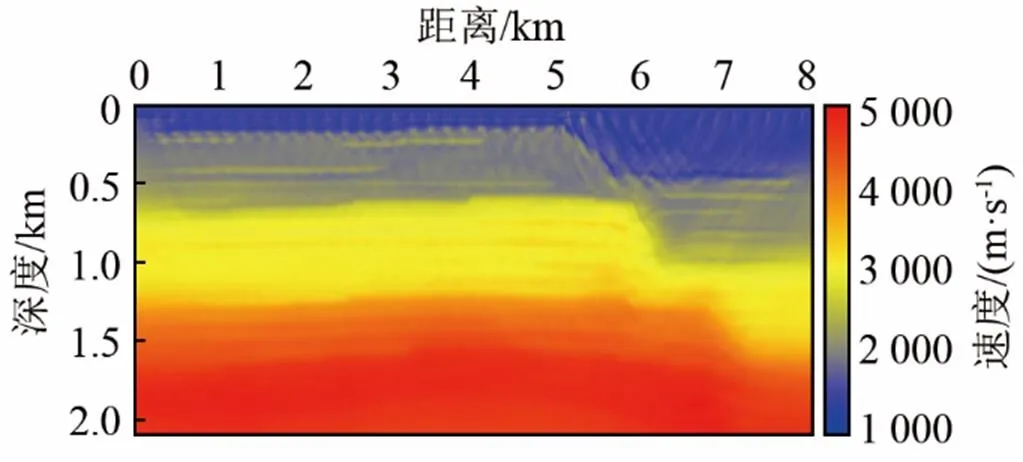
圖10 不依賴于子波的多尺度反演結果(復雜模型)

3 討論與結論

本文采用全波形反演方法對復雜模型進行速度場建模，能夠為高精度成像和解釋提供更加準確的速度場。針對波形反演中對子波準確度依賴較高和直接利用高頻數據反演的不穩定問題，本文通過修改維納濾波器，實現了一種不依賴于子波的多尺度全波形反演方法，模型試算證明了方法的正確性和有效性，在此基礎上得到以下結論：

(1) 由于以數據殘差為目標泛函，全波形反演需要準確的子波信息為前提，在子波不準確的情況下，波形反演難以提供有效的速度場更新。

(2) 傳統的時間域反演方法在地震數據主頻較高時容易出現反演效果不穩定以及周波跳躍的問題。采用反演頻率由低到高逐次遞進的反演策略是提高波形反演穩定性和反演效果的有效策略。

(3) 本文中方法通過修改維納濾波器，將不依賴于子波的反演策略與多尺度策略有機結合，一方面避免了波形反演對子波信息的依賴性，另一方面能夠在保證反演穩定性的基礎上提升反演精度。

然而，本文中方法還有一些需要改進之處。由于本文中方法是基于卷積模型，因此對于時變、空變子波的應用效果可能有限，這將是今后的研究重點之一。除此之外，本文中主要基于聲波介質，采用的正演方法為常密度聲波波動方程，將方法發展到彈性波等復雜介質也是今后的工作內容之一。

[1] VIRIEUX J, OPERTO S. An overview of full-waveform inversion in exploration geophysics[J]. Geophysics, 2009, 74(6): WCC1- WCC26.

[2] TARANTOLA A. Inversion of seismic reflection data in the acoustic approximation[J]. Geophysics, 1984, 49: 1259-1266.

[3] SHIN C, YOUNG H C. Waveform inversion in the Laplace domain[J]. Geophys. J. Int, 2008, 173(3): 922-931.

[4] SHIN C, YOUNG H C. Waveform inversion in the Laplace—Fourier domain[J]. Geophys. J. Int, 2009, 177: 1067-1079.

[5] 崔永福, 彭更新, 吳國忱, 等. 全波形反演在縫洞型儲層速度建模中的應用[J]. 地球物理學報, 2016, 59(7): 2713-2725.

CUI Yongfu, PENG Gengxin, WU Guochen, et al. Application of full waveform inversion velocity model-building technology for the frac-tured-vuggy reservoir[J]. Chinese J. Geophys(in Chinese), 2016, 59(7): 2713-2725

[6] 楊午陽, 王西文, 雍學善, 等. 地震全波形反演方法研究綜述[J].地球物理學進展, 2013, 28(2): 766-776.

YANG Wuyang, WANG Xiwen, YONG Xueshan, et al. The review of seismic full waveform inversion method[J]. Progress in Geophysics, 2013, 28(2): 766-776.

[7] 董良國, 遲本鑫, 陶紀霞, 等. 聲波全波形反演目標函數性態[J]. 地球物理學報, 2013, 56(10): 3445-3460.

DONG Liangguo, CHI Benxin, TAO Jixia, et al. Objective-function behavior in acoustic full-waveform inversion[J]. Chinese Journal of Geophysics, 2013, 56(10): 3445-3460.

[8] 王毓瑋, 董良國, 黃超, 等. 彈性波全波形反演目標函數性態與反演策略[J]. 石油物探, 2016, 55(1): 123-132, 141.

WANG Yuwei, DONG Liangguo, HUANG Chao, et al. Objective function be-havior and inversion strategy in elastic full-waveform inversion[J]. Geophysical Prospecting for Petroleum, 2016, 55(1): 123-132, 141.

[9] 王毓瑋, 董良國, 黃超, 等. 降低彈性波全波形反演強烈非線性的分步反演策略[J]. 石油地球物理勘探, 2016, 51(2): 288-294.

WANG Yuwei, DONG Liangguo, HUANG Chao, et al. A multi-step strategy for mitigating severe nonlinearity in elastic full-waveform inversion[J]. Oil Geophysical Prospecting, 2016, 51(2): 288-294.

[10] 董良國, 黃超, 遲本鑫, 等. 基于地震數據子集的波形反演思路、方法與應用[J]. 地球物理學報, 2015, 58(10): 3735-3745.

DONG Liangguo, HUANG Chao, CHI Binxin, et al. Strategy and application of waveform inversion based on seismic data subset[J]. Chinese Journal of Geophysics. 2015, 58(10): 3735-3745.

[11] CHOI Y, ALKHALIFAH T. Source-independent time-domain waveform inversion using convolved wavefields: Application to the encoded multisource waveform inversion[J]. Geophysics, 2011, 76(5): R125-R134.

[12] CHOI Y, SHIN C, MIN D J, et al. Efficient calculation of the steepest descent direction for source-independent seismic waveform inversion: An amplitude approach[J]. Journal of Computational Physics, 2005, 208(2): 455-468.

[13] LEE K H, KIM H J. Source-independent full-waveform inversion of seismic data[J]. Geophysics, 2003, 68(6): 2010-2015.

[14] BUNKS C, SALECK F M, ZALESKI S, et al. Multiscale seismic waveform inversion[J]. Geophysics, 1995, 60(5): 1457-1473.

[15] BOONYASIRIWAT C, VALASEK P, ROUTH P, et al. An efficient multiscale for time-domain waveform tomography[J]. Geophysics, 2009, 74(6): WCC59-WCC68.

[16] SIRGUE L, PRATT R G. Efficient waveform inversion and imaging: A strategy for selecting temporal frequencies[J]. Geophysics, 2004, 69(1): 231–248.

[17] FICHTNER A, TRAMPERT J. Hessian kernels of seismic data functionals based upon adjoint techniques[J]. Geophys. J. Int, 2011, 185 (2): 775-798

[18] PLESSIX R E. A review of the adjoint-state method for computing the gradient of a functional with geophysical applications[J]. Geophys. J. Int, 2006, 167(2): 495-503.

[19] 楊積忠, 劉玉柱, 董良國. 變密度聲波方程多參數全波形反演策略[J]. 地球物理學報, 2014, 57(2): 628-643.

YANG Jizhong, LIU Yuzhu, DONG Liangguo. A multi-parameter full waveform inversion strategy for acoustic media with variable density[J]. Chinese Journal of Geophysics, 2014, 57(2): 628-643.

[20] 劉璐, 劉洪, 張衡, 等. 基于修正擬牛頓公式的全波形反演[J]. 地球物理學報, 2013, 56(7): 2447-2451.

LIU Lu, LIU Hong, ZHANG Heng, et al. Full waveform inversion based on modified quasi-newton equation quasi-newton equation [J]. Chinese Journal of Geophysics, 2013, 56(7): 465-470.

[21] KIM Y, CHO H, MIN D J, et al. Comparison of frequency-selection strategies for 2D frequency-domain acoustic waveform inversion[J]. Pure & Applied Geophysics, 2010, 168(10): 1715-1727.

[22] YU H, ZHANG D, HUANG Y. Application of early arrival waveform inversion with pseudo-deconvolution misfit function by source convolution[J]. Inverse Problems in Science & Engineering, 2016, 25(1): 57-72.

[23] ZHOU C, SCHUSTER G T, HASSANZADEH S, et al. Elastic wave equation traveltime and waveform inversion of crosswell data[J]. Geophysics, 1997, 62(3): 853-868.

[24] 田坤, 黃建平, 李振春, 等. 多軸卷積完全匹配層吸收邊界條件[J]. 石油地球物理勘探, 2014, 49(1): 152.

TIAN Kun, HUANG Jianping, LI Zhenchun, et al. Multi-axial convolution perfectly matched layer absorption boundary condition [J]. Oil Geophysical Prospecting, 2014, 49(1): 143-152.

[25] 黃建平, 楊宇, 李振春, 等. 幾種自由邊界實施方法在完全匹配層條件下的對比研究[J]. 地震學報, 2014, 36(5): 964-977.

HUANG Jianping, YANG Yu, LI Zhenchun, et al. Comparative study among implementations of several free-surface boundaries with perfectly matched layer conditions[J]. Acta Seismologica Sinica, 2014, 36(5): 964-977.

Acoustic source-independent multi-scale full waveform inversion

ZHOU Min1, WU Jie2

(1. Department of Modern Physics, University of Science and Technology of China, Hefei 230026, Anhui, China; 2. State Key Laboratory of Particle Detection & Electronics, University of Science and Technology of China, Hefei 230026, Anhui, China)

As the most accurate and promising model building method, acoustic full waveform inversion is expected to provide a more effective velocity model. However, full waveform inversion is a data-driving inversion method, which needs accurate source wavelet term and low frequency data. In this paper, a source independent inversion strategy is proposed by modifying the Wiener filter using the reference trace. By filtering the modeled and observed data, the source term can be eliminated from the misfit function. Besides, because the target wavelet in the modified Wiener filter can be chosen relatively freely, the new method is naturally combined with the frequency based multi-scale inversion strategy to further improve the stability of full waveform inversion. The proposed method is applied in practical application to verify its correctness and efficiency. The theoretical analysis and numerical test illustrate that the new method can avoid the source estimating procedure and improve the inversion accuracy and stability of full waveform inversion, which outperforms the conventional full waveform inversion strategy.

velocity model building; full waveform inversion; source-independent; multi-scale inversion strategy

P631.4

A

1000-3630(2018)-06-0521-07

10.16300/j.cnki.1000-3630.2018.06.002

2018-05-22;

2018-06-30

國家自然科學基金資助項目(41574106)、國家科技重大專項(2017ZX05008-008-041)、國家重大科研裝備研制項目(ZDYZ2012-1-05-03)。

周敏(1993－), 女, 山東濰坊人, 碩士, 研究方向為全波形反演方法。

武杰,E-mail: wujie@ustc.edu.cn