球面聚焦聲場自易法從GB/T 32522-2016到IEC TS 62903-2018的技術(shù)進步

壽文德，胡濟民，余立立，胡兵

?

球面聚焦聲場自易法從GB/T 32522-2016到IEC TS 62903-2018的技術(shù)進步

壽文德1,2，胡濟民3，余立立4，胡兵1

(1. 上海醫(yī)學超聲研究所，上海 200233；2. 上海交通大學，上海 200030；3. 江蘇省醫(yī)療器械檢驗所，江蘇南京 210022；4. 上海海事大學，上海 201306)

文章敘述了《球面聚焦超聲換能器的電聲特性和聲功率測量》的自易法校準成為國家標準方法后，進而以其為基礎(chǔ)在起草國際電工委員會技術(shù)規(guī)范的過程中，所做的主要技術(shù)進步，包括：理論敘述的改進、一些錯誤概念的修正、最新研究成果的吸納、全頻段實驗驗證、測量不確定度估計等重要方面。

自易法；球面聚焦超聲場；電聲參數(shù)測量；國際電工委員會技術(shù)規(guī)范；標準方法

0 引言

自從2002年創(chuàng)立球面聚焦超聲換能器的自易校準法后，在國內(nèi)同行專家們的共同努力下，2014年完成了相關(guān)國家標準的起草工作，發(fā)布了GB/T 23522-2016《聲學 壓電球面聚焦超聲換能器的電聲特性及其測量》。2015年以我國國家標準為基礎(chǔ)，成功申請到了起草IEC TS 62903 Ed1.0: 2018《Ultrasonics-Measurements of electroacoustical param- eters and acoustic output power of spherically curved transducers using self-reciprocity method》的中國國家提案(Nation Project, NP)項目。經(jīng)兩年多的工作，特別是在與德國聯(lián)邦技術(shù)物理研究院(Physikalisch- Technische Bundesanstalt,PTB)超聲理論專家K Beissner的理論交流和融合過程中，技術(shù)上有了重要的實質(zhì)性改進，規(guī)范方法更趨完善，已于2018年1月出版發(fā)行。本文就IEC TS中對GB/T的實質(zhì)性技術(shù)修改補充，做概略介紹。希望讀者在執(zhí)行國家標準時，能對實驗做必要的改進，以免出錯。

1 基本方法

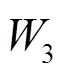
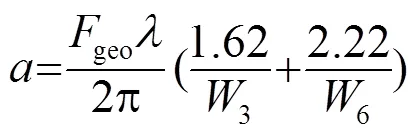
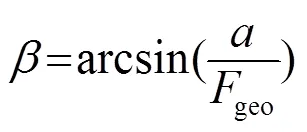
在IEC TS 中糾正了GB/T中將測量中的焦平面規(guī)定為最大聲壓焦平面(焦距pres)的錯誤，而將其規(guī)定為幾何焦平面和幾何焦距geo。理由是：geo是發(fā)射球面的曲率半徑，是常數(shù)。pres是隨聲速和頻率改變的變量。所有聚焦換能器聲場的理論，都是基于geo=發(fā)展起來的。在適用頻率的低端500 kHz時，這兩個焦距存在較大的差別。這一修改，反而簡化了測量步驟。無需再用水聽器尋找geo。據(jù)此，在整個IEC TS中只使用幾何焦距和幾何焦平面，原來GB/T中的所有pres符號全部改成geo。

第二步，水槽里在被測換能器的幾何焦平面附近設(shè)置不銹鋼平面反射器。使用猝發(fā)聲信號發(fā)生器激勵換能器，調(diào)節(jié)換能器的距離、方位和俯仰角，使其收到的第一回波信號最大，且回波渡越時間與聲速的乘積是2geo。測量系統(tǒng)如圖1所示。

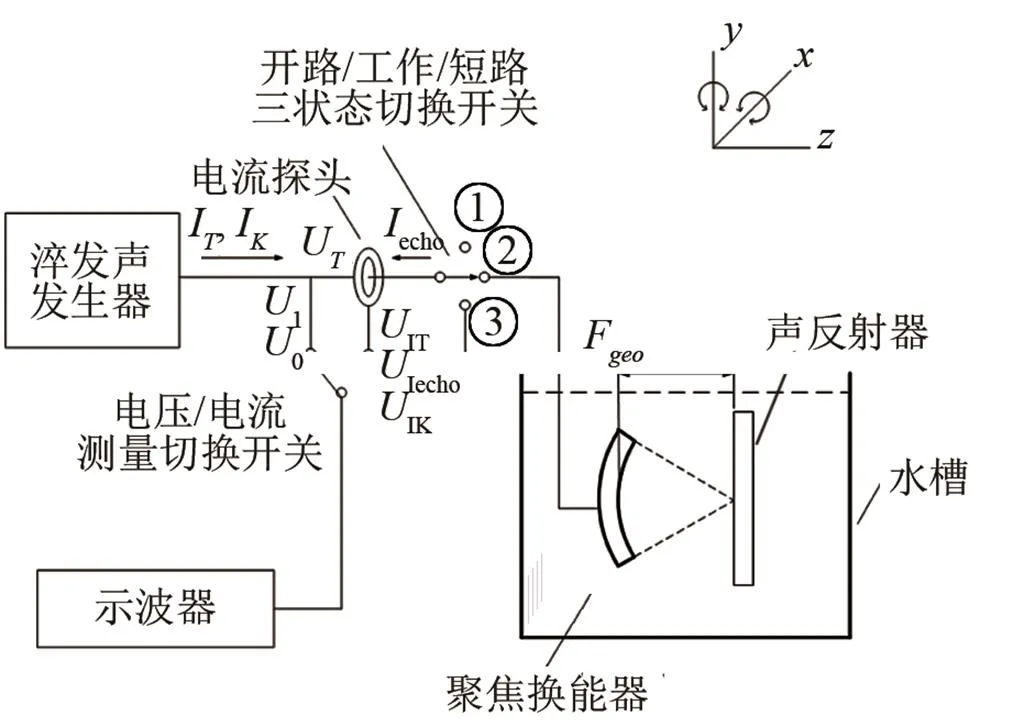
圖1 自易法測量球面聚焦換能器的電聲參數(shù)和聲功率的裝置示意圖

發(fā)射電流響應(yīng)：

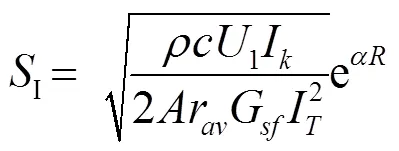
Fig.2 Waveshapes of measured voltage and current in self-reciprocity calibration for a spherically curved focusing trnsducer

發(fā)射電壓響應(yīng)：

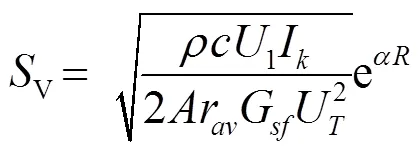
電壓靈敏度：

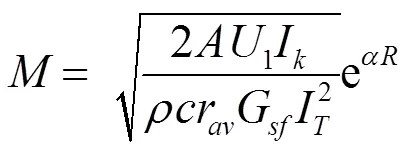
輸出聲功率：

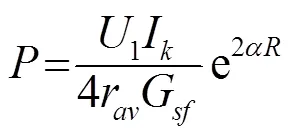
輻射電導(dǎo)：

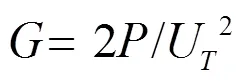
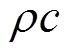
2 規(guī)范了球面自聚焦換能器自易法校準和聲功率測量的適用范圍

2.1 頻率范圍

用自易法對頻率為500 kHz、1.92 MHz、5 MHz、10 MHz、15 MHz的5種換能器做了測量，做了重復(fù)性試驗(=6)。取得了一系列測量數(shù)據(jù)和不確定度估計值，驗證了規(guī)范預(yù)設(shè)0.5～15 MHz范圍的適用頻率范圍和測量不確定度參考值(見表1)。

2.2 規(guī)定了適用的被測換能器線性范圍的準則和檢驗方法

為保證被測換能器在線性范圍內(nèi)工作，規(guī)范中補充了如下內(nèi)容：

(2) 換能器的線性范圍檢驗：在換能器表面黏貼小片聚偏氟乙烯(Polyvinylidene Fluoride, PVDF)，傳感器，用來測定表面振幅信號，要求值起伏≤5%。

2.3 衍射修正系數(shù)數(shù)值表列表的適用范圍：

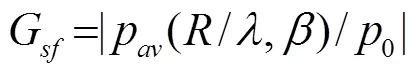
式(8)中：為換能器的虛象面(見圖3)上的平均聲壓。

(1) 聚焦半角范圍

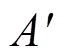
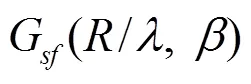
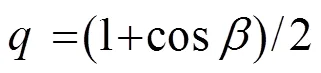
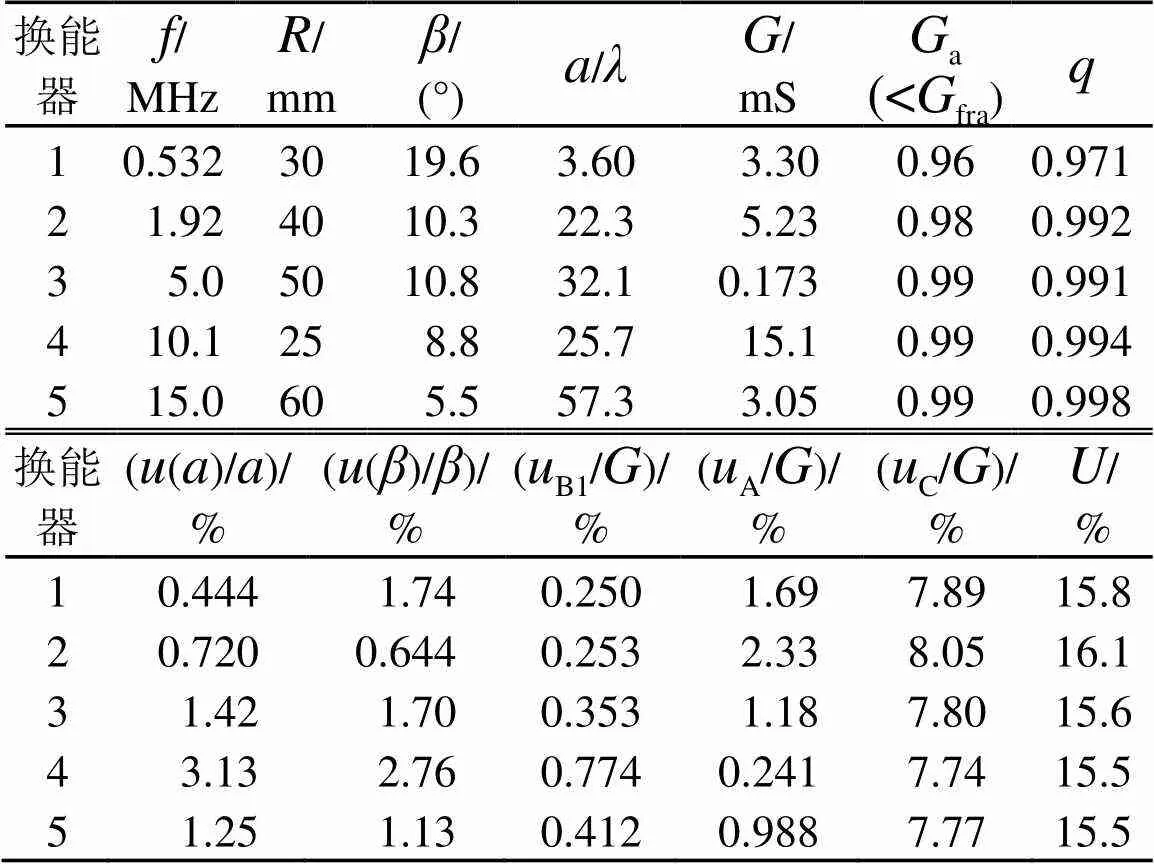
表1 5個換能器的測量結(jié)果和不確定度估計數(shù)據(jù)

(3) 聲功率測量法的理論基礎(chǔ)完善和計算準確性依據(jù)

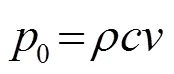
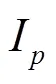
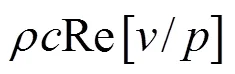
借助于同濟大學錢夢騄等的實驗結(jié)果[7]和武漢數(shù)學物理所程建政等的研究[8]，我們斷定在幾何焦域附近，聲波是近似呈平面行波的波陣面?zhèn)鞑サ摹Ｒ虼嗽趲缀谓蛊矫嬷行母浇拱吒浇母鼽c處聲壓與質(zhì)點振速的相位差是相同的，聲壓是以Jinc函數(shù)方式分布的。

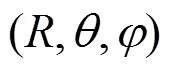
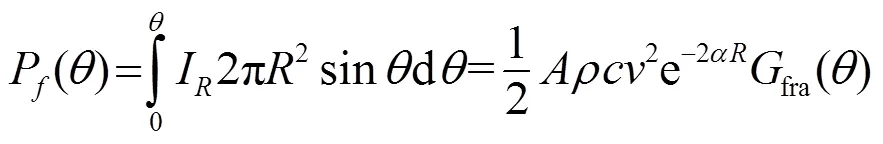
其中：為總聲功率P中通過球缺面的那部分聲功率所占的分數(shù)。

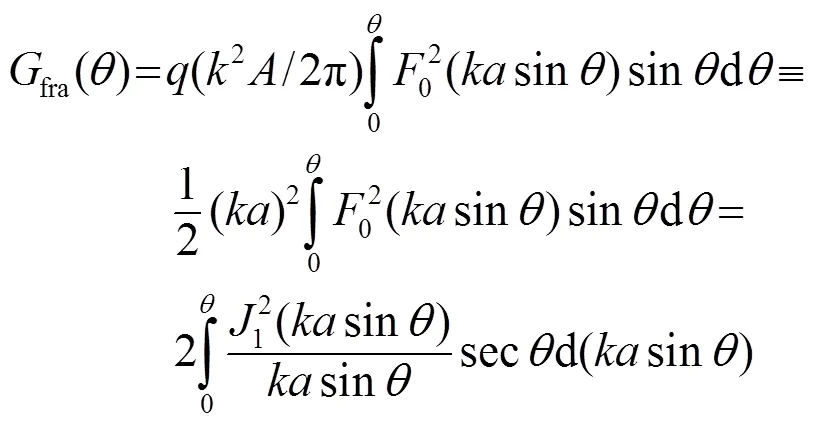
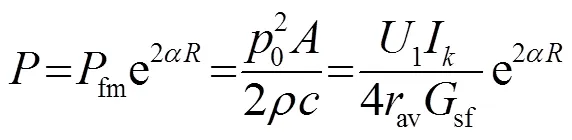
當較小時，即≈0，sec≈1，則

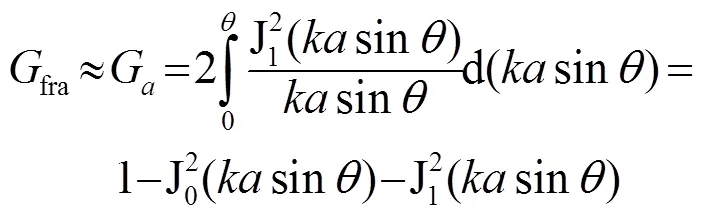
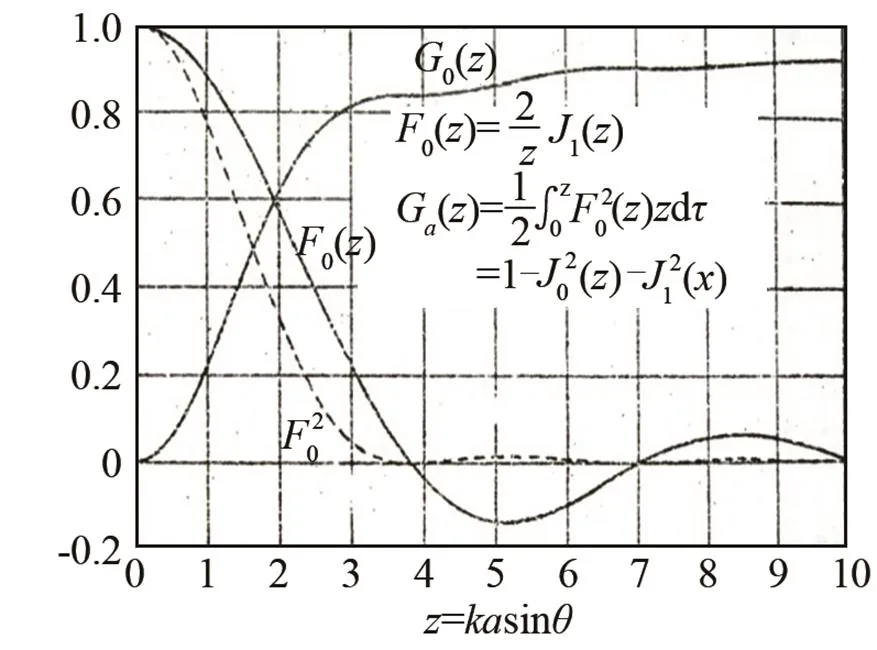
圖5 在幾何焦平面上的函數(shù)Ga(kasinθ), 衍射圖案F0(kasinθ) 和F02(kasinθ)[6]

(注：圖5中的橫坐標=sin即為本文中的)

Fig.5 The functions ofG(sin), diffraction pattens of0(sin) and02(sin) on geometric focal plane[6]

(Note: abscissa=sinin Fig.5, i.e.in the text)

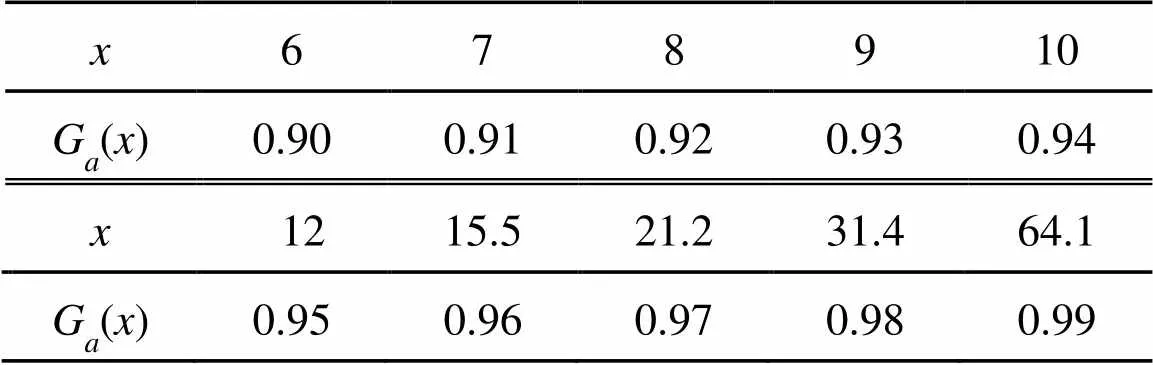
表2 在β≤45°條件下與不同的x = kasinθ值相應(yīng)的Ga數(shù)值表 (按照O’Nail的公式(12)求得，見參考文獻[6])

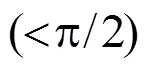
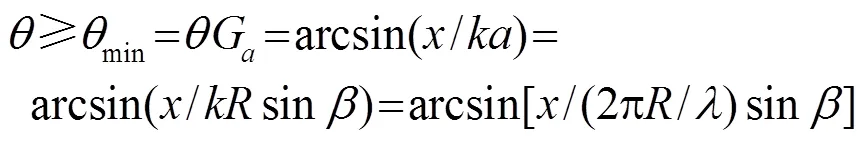
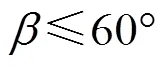
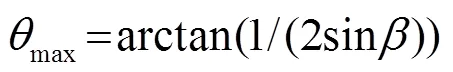
因此同時滿足式(13)、(14)的聲強積分上限應(yīng)該符合下列不等式：

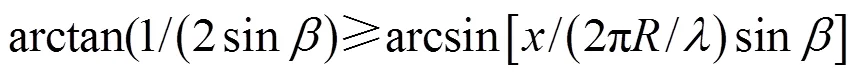
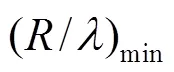
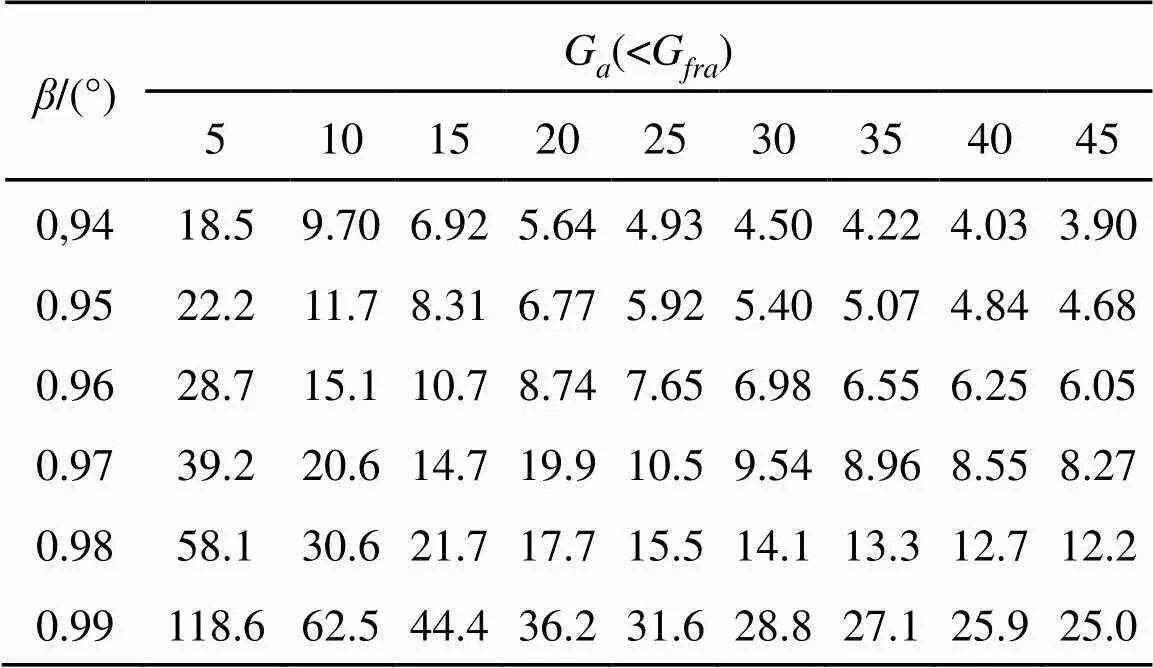
表3 對應(yīng)于Ga= 0.94, 0.95, 0.96, 0.97, 0.98, 0.99和β的 (R/λ)min數(shù)值表

注: ()min=/{2psinsin[arctan(1/2sinβ)]}數(shù)值分別對應(yīng)于G=0.94. 0.95. 0.96. 0.97. 0.98. 0.99 (即=sin=10, 12, 15.5, 21.2, 31.4, 64.1)

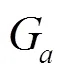
3 結(jié)束語

由國家標準向國際規(guī)范升級的過程中，在理論敘述的改進、一些錯誤概念的修正、最新研究成果的吸納、全頻段實驗驗證、新測量細則的增補、測量不確定度估計等重要方面取得了重要的技術(shù)提高。實現(xiàn)了從粗放型標準向精確型標準的跨躍。把我國創(chuàng)立的球面自聚焦換能器的自易校準法推廣到世界，成為IEC國際規(guī)范的標準方法。

致謝 在起草IEC 技術(shù)規(guī)范的過程中，Klaus Beissner、Volker Wilkens和Tim Etchells以及德國、日本、俄羅斯和捷克的國家委員會都作出了許多貢獻。還得到了邢廣振、楊平、錢夢騄、程茜、張德俊、杜功煥等專家在實驗和學術(shù)上的支持，特致謝忱。

[1] JJF 1059.1-2012 測量不確定度的評定與表示[S].

[2] BEISSNER K. Some basic relations for ultrasonic fields from circular transducers with a central hole[J]. Acoust. Soc. Am., 2012, 131(1): 620.

[3] SAPOZHNIKOV O A, SINILO T V. Acoustic field produced by a concave radiating surface with allowance for the diffraction[J]. Acoust. Phys., 2002, 48(6): 720-727.

[4] SHOU W, DUAN S, HE P, et al. Calibration of a focusing transducer and miniature hydrophone as well as acoustic power measurement based on free field reciprocity in a spherically focused wave field[J]. IEEE Trans.on UFFC, 2006, 53(3): 564-570.

[5] 壽文德, 余立立, 段世梅, 等. 球面聚焦超聲換能器的電聲特性和測量方法研究[J]. 聲學技術(shù), 2013, 32(5): 379-389.

SHOU Wende, YU Lili, DUAN Shimei, et al. Self-reciprocity calibration method of ultrsonic transducer as well as its application in power measurement and relation with radiation force balance method[J]. Technical Acoustics, 2014, 33(5): 445-453.

[6] O’NEIL, H T. Theory of focusing radiator[J]. Acoust. Soc. Am., 1949, 21(5): 516-526.

[7] 徐崢, 陳皓, 錢夢騄, 等. 點聚焦聲場的三維紋影法成像研究[J].聲學技術(shù), 2014, 33(2): 202-204.

XU Zheng, CHEN Hao, QIAN Menglu, et al. Visualization of point-focusing ultrasonic field by three-dimensional schlieren method[J]. Technical Acoustics, 2014, 33(2), 202-204.

[8] 程建政, 周玉祿, 毛彥欣, 等. 基于瑞利積分疊加法的聚焦換能器聲場特性研究[J]. 計算物理, 2008, 25(4): 293-298.

CHEN Jianzheng, ZHOU Yulu, MAO Yanxin, et al. Study of acoustic field characteristics of focusing transducer based on the super-position method of Rayleigh integral[J]. Chinese Journal of Computational Physics, 2008, 25(4): 293-298.

[9] CATHIGNOL D, SAPOZHNIKOV O A. On the application of the Rayleigh integral to the calculation of the field of a concave focusing radiator[J]. Acoust. Phys., 1999, 45(6): 735-742.

[10] BEISSNER K. On the lateral resolution of focused ultrasonic fields from sphericallycurved transducers[J]. J. Acoust. Soc. Am., 2013, 134(5): 3943.

The technical progress of self-reciprocity method into IEC TS62903-2018 from GB/T32522-2016

SHOU Wen-de1，2, HU Ji-min3, YU Li-li4, HU Bing1

(1. Shanghai Institute of Ultrasound in Medicine, Shanghai 200233, China; 2. Shanghai Jiao Tong University, Shanghai 200030, China;3. Jiangsu Province Institute for Medical Equipment Testing, Nanjing 210022, Jiangsu, China;4. Shanghai Maritime University, Shanghai 201306, China)

This paper describes the major technical improvements in drafting IEC TS 62903 Ed1.0: 2018 based on GB/T 32522-2016, in which the self-reciprocity calibration method is defined as the national standard method in China. These improvements include the theoretical expression, the corrections of some error concepts, applications of new research results, the experimental verification in full frequency range, and the evaluation of measurement uncertainty etc.

self-reciprocity method; spherically focused ultrasonic field; electroacoustical parameter measurement; Technical Specifications for the International Electrotechnical Commission (IEC-TS); standard method

TB552

A

1000-3630(2018)-06-0607-05

10.16300/j.cnki.1000-3630.2018.06.017

2018-03-04;

2018-06-16

壽文德(1941－), 男, 浙江諸暨人, 教授, 研究方向為生物醫(yī)學超聲學與標準化。

壽文德, E-mail: wdshou@163.com