分數除法算理表征方式的選擇：教師的視角

王敏 吳敏霞 趙雨晴 鞏子坤

【摘? ?要】采用問卷調查，了解44名教師選擇的“易于學生理解分數除法算理的表征方式”。調查結果顯示：教師認為對學生而言，直觀表征最容易理解，抽象表征比較容易理解，形式表征最不容易理解。隨著任務難度增加，教師選擇的分數除法算理表征方式會發生變化，即在同一模型（平均分，包含除，下同）中，直觀表征的平均分呈下降趨勢，形式表征的平均分呈上升趨勢，抽象表征的平均分變化不大。教師認為我們所提供的由7個任務構成的學習路徑是合理的，符合由易到難的規律。

【關鍵詞】教師;分數除法算理;表征方式;學習路徑

一、引言

運算能力是一項重要的素養。王光明等指出：運算正確、合理是運算能力的主要特征，理解算理是學生正確地、迅速地運算的基礎[1]。因此，運算能力，不僅包括能正確地運算，更包括理解算理[2]。

分數知識是小學數學中很重要的內容，“分數除法”又是分數學習的重中之重[3]。對于分數除法而言，掌握法則很容易，而理解算理比較困難[4]。H·Wu指出，教師在進行分數除法教學時往往要求學生記住“顛倒相乘”的運算法則，這種忽視數學基本原則的教學使得數學學習變成死記硬背的學習，失去它原有的意義[5]。這導致有些學生在進行分數除法運算時，出現把被除數的分子分母顛倒再與除數相乘的錯誤，這是學生沒有理解分數除法算理導致的[6]。

因而，如何使學生在理解算理的基礎上，掌握法則，進而實現“算理貫通、理法融合”，是一項重要的研究課題。這就需要我們提供適合的表征分數除法算理的方式，設計合理的學習任務序列（即學習路徑）[7][8]，以幫助學生理解算理，提升運算能力。鞏子坤團隊通過行動研究法，得到了有利于學生理解算理的學習路徑，包括：分數除以整數[9];一個數除以分數 [10] 。

另外，研究顯示：表征是判斷學生對某個數學概念是否理解的重要證據[11]。理解分數除法算理，也就是能用多種表征方式來解釋和說明運算法則的合理性。鞏子坤等的研究表明，有四種表征方式（程序表征、直觀表征、抽象表征、形式表征）[12][13][14]。本研究主要選擇后三種。

我們常常說“以學定教”，就是說，要從學生的知識基礎與認知特點出發，設計合理的任務序列即學習路徑，采用合適的表征方式。對于分數除法的教學亦然。因此，借鑒鞏子坤團隊設計的問卷，從教師的視角，探查在教師的心目中：（1）學生易于理解的表征分數除法算理的方式是什么？隨著任務難度的變化，這些表征方式變化的趨勢是什么？（2）合理的學習路徑是什么？

二、研究設計

（一）研究對象

選擇來自四所不同學校的44名教師，其中男教師17名，女教師27名;23名教師教過分數除法，21名教師沒有教過分數除法。教齡在0-5年的教師10名，在6-10年的8名，在11-15年的4名，在16-20年的12名，20年以上的10名。

（二）問卷編制

問卷由兩部分構成，第一部分是選擇題，一共7個任務。任務1到任務3為分數除以整數，采用平均分模型，即分數除以整數（被除數的分子能夠被整除），單位分數除以整數，分數除以整數（被除數的分子不能被整除）;任務4到任務7為一個數除以分數，采用包含除模型（任務4到任務6為整數除以分數，分別為1除以單位分數、1除以非單位分數、整數除以分數;任務7為分數除以分數）。每個任務有三個選項，分別是直觀表征、抽象表征和形式表征，請教師選擇最容易理解、比較容易理解和最不容易理解的表征方式，并要求說明選擇時的理由。

任務1至任務7分別為：[23]÷2，[12]÷3，[23÷5]，1÷[13]，1÷[23]，3÷[23]，[45]÷[23]（省略了情境）。

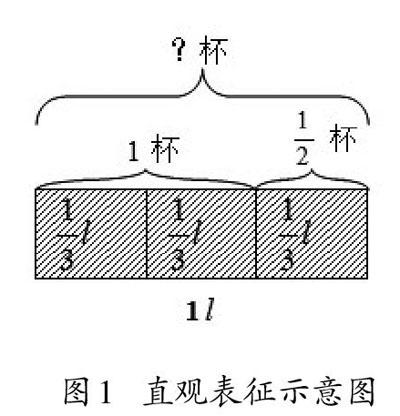
以任務5為例，玻璃杯的容量是[23l]。現有[1l]牛奶，可以倒入多少玻璃杯？

（1）直觀表征。

圖1? ?直觀表征示意圖

由圖1可以看出： [1÷23=32（杯）]。

（2）抽象表征。

玻璃杯的容量是[23][l]，1[l]牛奶里有多少[23l]呢？

1[l]牛奶里有1個[23l];還剩[13l]。

[23l]可以裝1杯;剩下的[13l]，是[23l]的一半即[12]，所以可以裝[12杯]。

所以，1[l]牛奶可以裝[1+12=32（杯）]。

所以，[1÷23=32（杯）]。

（3）形式表征。

[1÷23=（1×32）÷（23×32）=（1×32）÷1=1×32=32（杯）]。

問卷第二部分請教師選擇問卷中呈現的分數除法的學習路徑是否合理，若不合理，請提供新的任務序列。

（三）研究方法

問卷法和訪談法相結合。在教師完成問卷之后，通過訪談進一步了解教師選擇各種表征方式的理由以及對問卷提供的學習路徑的看法。

對教師的選擇進行賦分，最容易理解的表征方式賦為3分，比較容易理解的賦為2分，最不容易理解的賦為1分。對教師的選擇理由進行分類編碼，如表1所示，2-2表示教師認為提供的表征方式比較復雜，學生不容易理解。

表1? ?理由分類表

[分類 定義 1學生 1直觀程度 1直觀 表征方式的直觀或抽象程度 2抽象 2知識遷移 已有知識的影響，如學校學到的知識及生活中獲得的經驗等 3知識應用 對商不變性質等知識的直接應用，如模仿或直接代入計算 2任務 1簡潔 問卷呈現的不同表征方式的復雜程度 2煩瑣 ]

對各個變量的測量指標進行信度分析，直觀、抽象、形式表征的cronbach's α系數分別為0.735、0.778、0.785，均大于0.7，問卷具有較好的內部一致性。

三、研究結果

（一）三種表征方式

1. 三種表征方式的得分情況

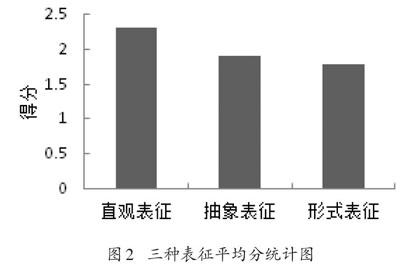
對教師選擇的三種表征的平均分進行統計（見圖2），發現教師選擇的直觀表征的得分最高，抽象表征其次，形式表征得分最低。說明教師認為直觀表征對學生來說最容易理解，抽象表征比較容易理解，形式表征最不容易理解。

圖2? ?三種表征平均分統計圖

2.三種表征方式的水平

為了分析教師選擇的三種表征的差異性情況，通過傅萊德曼（Friedman）檢驗分析表征的水平，結果顯示三種表征得分具有顯著性差異[X2（2）=10.686，p<.05]。成對比較分析顯示，教師選擇直觀表征和抽象表征（[p=0.236]），抽象表征和形式表征（[p=0.450]）均不存在顯著性差異，即直觀表征和抽象表征、抽象表征和形式表征分別在同一個水平;直觀表征和形式表征（[p<.05]）存在顯著性差異，即直觀表征和形式表征不在同一個水平。

由此可見，教師認為對學生而言，直觀表征與形式表征水平相差較大，直觀表征與抽象表征、抽象表征與形式表征差距較小。形式表征得分最低，說明形式表征最不容易理解。因此，總體來看，形式表征處于最高理解水平，抽象表征在中等水平，直觀表征處于最低理解水平。

（二）不同任務的三種表征方式

1. 不同任務三種表征方式的得分情況

計算每個任務下直觀表征、抽象表征、形式表征三種表征的平均分（見圖3）。可以看出，在同一模型中，直觀表征的得分呈下降的趨勢，形式表征的得分呈上升的趨勢，而抽象表征的得分一直處于比較平穩的狀態。說明同一模型中，隨著任務難度增加，教師選擇的最容易理解的表征方式由直觀表征漸漸轉向形式表征。

圖3? ?不同任務三種表征方式的得分情況統計圖

2. 不同任務三種表征方式的水平

通過傅萊德曼（Friedman）檢驗分析每個任務下教師三種表征水平的差異性情況，結果顯示，任務1-4和任務7下教師選擇三種表征得分具有顯著性差異[任務1、2、3、4、7的[X2（2）]值分別為：[44.909，][24.045，6.045，31.955，10.686] ，所有[p<.05]]。任務5和任務6，結果顯示保留原假設，表明對于這兩個任務，教師選擇的三種表征都在同一個水平。

成對比較分析顯示，任務2和任務4，三種表征兩兩均不在同一個水平（所有[p<.05]）。任務1，抽象表征和形式表征（[p=0.057]）在同一個水平，直觀表征和抽象表征、形式表征（[p<.05]）均不在同一個水平。任務3，直觀表征和抽象表征（[p=0.497]）在同一個水平，形式表征和直觀表征、抽象表征（[p<.05]）均不在同一個水平。任務7，直觀表征和抽象表征（[p=0.859]）在同一個水平，形式表征和直觀表征、抽象表征（[p<.05]）均不在同一個水平。

綜上，從任務1到任務3，表征水平由直觀表征與另兩種表征均不在同一個水平，轉變為直觀表征與抽象表征在同一水平。說明隨著任務越來越難，三種表征之間水平差距逐漸減小。從任務4到任務7同樣如此。任務7，形式表征已經處于最低理解水平，說明隨著難度增加，教師認為形式表征更利于學生理解。

3. 學習路徑

被調查的44名教師中，有43名教師認為可以按照任務1-7的順序進行教學，只有一位教師認為不可以，但卻沒有提供新的順序。有9名教師提供了簡化方案。教師提供的簡化方案大致是任務1、任務3、任務4、任務6、任務7的順序，也是按照分數除以整數、整數除以分數、分數除以分數的順序進行編排。

四、討論與分析

（一）最容易與最不容易理解的表征方式

以下對教師選擇三種表征時給出的理由類型進行分析。將每種理由被提供的次數進行了統計，如圖4。

圖4? ?三種表征理由分布圖

可以發現大多數教師選擇直觀表征是因為畫圖比較直觀，清晰明了。選擇抽象表征是因為語言解釋是學生經常接觸到的，利于知識遷移。選擇形式表征是因為商不變規律直接應用比較方便，并且一部分教師認為形式表征比較抽象，所以相對直觀表征和抽象表征，形式表征比較困難。

（二）不同任務表征方式的變化趨勢

隨著任務的變化，直觀表征的得分越來越低。為深入了解教師選擇的理由，選取一位教師的訪談內容，如下（T1表示訪談者，T2表示被訪談教師）：

T1：對于任務5：[1÷23]，你說1除以一個非單位分數雖然直觀，但不是整數倍，所以有困難。這是指什么？

T2：反應快的學生，會認識到這個[13]正好是半杯，但是反應慢的就不知道[13]l到底是多少杯。實際上要用[13÷23]，因為一杯是[23]l，[13]l是[23]的一半。這個圖讓他自己畫的話，就困難，這時用圖反倒不好理解。

從上述訪談中，可以發現對于分數除以整數的任務，當被除數的分子不能被整數整除時，圖形并不好畫。直觀表征雖然能夠清晰地看出問題的答案，但有時在操作過程中難以實施。

抽象表征得分一直變化不大。教師選擇抽象表征是因為語言解釋是一種常見的方式，所以抽象表征的得分并不會隨任務難度不同而發生明顯波動。

形式表征得分在同一模型中的得分越來越高。教師認為在前面任務中有所鋪墊了，那么商不變規律符合學生知識遷移的思維習慣，更容易理解。所以在后面的任務中才會逐漸選擇形式表征，如下面這段訪談記錄。

T2：我覺得這三種方法運用于商不變性質一看就知道。因為我是打通來考慮的，從任務1開始為商不變性質做了鋪墊，所以說到任務5的時候再用商不變規律就很自然了。

可見形式表征作為一種理解算理的方法，是在學生具備了一定的認知基礎后，才比較容易被接受。所以教師在前幾個任務中并沒有傾向于選擇形式表征。

（三）學習路徑

教師基本認為可以按照分數除以整數、整數除以分數、分數除以分數的順序進行教學。教師認為這是“從易到難的順序”“7個任務的設計比較完善”。學生學過整數除以整數，對除法的理解就是平均分，因此從分數除以整數可以理解為將分數平均分開始，再到整數除以分數、分數除以分數，符合學生認知規律。

五、結論與建議

（一）結論

（1）教師對三種表征方式的選擇變化分成兩段，呈類似趨勢。

在同一模型中，隨著任務難度增加，直觀表征的平均得分呈下降趨勢，形式表征逐漸上升，抽象表征變化不大。教師選擇的最容易理解的表征方式從直觀表征轉向形式表征。

（2）教師選擇的最容易理解的表征方式隨著任務不同有所不同。

任務1到任務4，教師選擇的最容易理解的表征方式是直觀表征。從任務5開始漸漸認為形式表征比較容易理解，到任務7認為形式表征最容易理解。所以對于分數除法的教學，并不能選擇一種表征方式一以貫之。

（3）7個任務構成的學習路徑有其合理性。

任務1-7的教學順序將教學難點，即分數除法的教學內容進行了合理拆分，引導學生對分數除法的各種情況進行逐一分析、總結、探究，從而降低教學難度，有利于學生的理解。

（二）建議

問卷中提供的任務序列得到了44位被試者的一致認可，說明該任務序列是可行的。而對于不同的任務，可以選擇不同的表征方式進行教學。

任務1到任務4中，直觀表征和抽象表征得分高于形式表征;建議教師對于完成這些任務，首選直觀表征，其次選擇抽象表征。

任務5和任務6中，直觀表征得分最高;任務5形式表征的得分超越抽象表征。建議教師此時開始鋪墊商不變規律，即任務5和任務6選擇直觀表征，輔之以形式表征解釋算理。

任務7，屬于分數除以分數，是7個任務中難度最大的。形式表征得分最高。建議教師首選形式表征，輔之以抽象表征解釋算理。

參考文獻：

[1]王光明，范文貴.《義務教育課程標準（2011年版）》解析與教學指導叢書[·]新版課程標準解析與教學指導（小學數學）[M].北京：北京師范大學出版社，2012.

[2]中華人民共和國教育部.義務教育數學課程標準（2011年版）[M].北京：北京師范大學出版社，2012.

[3]葛敏輝. 理解視域下“分數除法”計算教學認知起點的調查分析[J]. 小學數學教師， 2018（3）.

[4]徐斌. 形象支撐 溝通聯系 理解本質——六年級上冊“分數除法”教材解析與教學建議[J]. 小學數學教育，2015（Z4）：53-56.

[5]H.Wu.The Mis-Education of Mathematics Teachers[J].Notices of the AMS， 2011，Volume 58（3）：372-384.

[6]鞏子坤. 有理數運算的理解水平及其教與學的策略研究[D].重慶：西南大學，2006.

[7] Andreas Schulz，Timo Leuders. Learning trajectories towards strategy proficiency in multi-digit division – A latent transition analysis of strategy and error profiles[J]. Learning and Individual Differences，2018.

[8]Hui Jin，Jamie N. Mikeska，Hayat Hokayem，Elia Mavronikolas. Toward coherence in curriculum， instruction， and assessment： A review of learning progression literature[J]. Science Education，2019，103（5）.

[9]鞏子坤，盧子苓，靳培英，等.分數除以整數學習路徑優化的實證研究[J].小學數學教師，2019（2）：75-81.

[10]李津. 基于學習路徑優化的教學設計研究[D].杭州：杭州師范大學，2016.

[11]原登慧，李俊.理解遠不止于會計算[J].數學教育學報，2011，20（1）：55-57.

[12]鞏子坤.理解視閾下的分數除法課程目標的實證研究[J].教育探索，2010（1）：70-73.

[13]鞏子坤.“小數乘法運算”課程目標：基于學生的理解水平[A]. 全國數學教育研究會，2010：9.

[14]鞏子坤.學生學習小數乘法的基礎研究[J].小學數學教師，2017（10）：66-71.

（杭州師范大學理學院? ?311121

杭州師范大學經亨頤教師教育學院? ?311121）