數學習題編制策略

楊勁芳

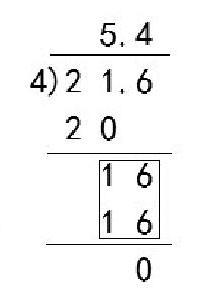
在數學教學中，練習和測驗是必不可少的環節，對教學起著導向作用。如何讓數學習題、試題編制更科學，以下策略供大家在編制試卷、習題時參考。

一、減少死記，關注知識技能的本源化

純粹的計算題對部分學生來講或許帶有一定的機械模仿性，有時不妨換一個方式，考查一下學生是否真正理解計算過程中每一個數據的來龍去脈，變形式化的掌握為理解性的掌握。

【例1】

原題：列豎式計算21.6÷4。

現題：在右邊的除法豎式中，方框內的16表示16個（? ）。

A.1? ? ?B. 0.1? ? ? C. 0.01? ? ? D.0.001

二、注重變式，提供知識應用的新情境

“基礎”并不等同于“簡單”，教師在命題過程中，可以給習題換個“馬甲”，多創造一些適合知識運用的新情境。

【例2】

原題：A÷B=C（B≠0），則A=? ? ? ? ? 。

現題：A÷B=C（B≠0，C≠0），則B×C÷A=? ? ? ? ? ?。

原題和現題考查的知識點都是乘除法之間各部分的關系，現題給學生一個新的情境：兩個相同的數相除（0除外），商為幾？

【例3】

原題：某次語、數測驗有21名學生至少一門功課達到了優秀，其中語文優秀的有16人，數學優秀的也有16人，語、數都優秀的有幾人？

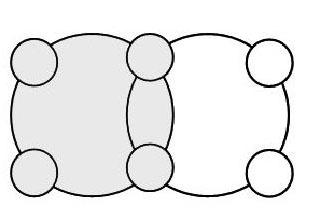
現題：將1、2、3、4、5、6六個數字填入圖中的小圓圈內，使每個大圓圈上四個數字的和都是16。

兩道題都可用“16+16-（1+2+3+4+5+6）=11”解決，在現題中，11是重疊部分的總和，中間重疊的圈內只能填5和6，所以邊上兩數之和是5，填1、4和2、3。現題在數陣圖與韋恩圖之間架起了橋梁，幫助學生領悟重疊問題的本質特征。

三、改變習題信息的呈現方式

試卷編制中，如果通篇都是用文字表達信息，會給人帶來視覺疲勞。這時可適當改變信息的呈現方式，圖文結合，也可考查學生的綜合能力。

（一）圖式方式呈現

【例4】

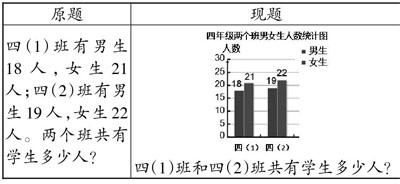
[原題 現題 四（1）班有男生18人，女生21人;四（2）班有男生19人，女生22人。兩個班共有學生多少人？

四（1）班和四（2）班共有學生多少人？ ]

將文字敘述題以統計圖的形式呈現，培養學生讀圖提取信息的能力，也便于學生在計算總人數時，較為直觀地交換加數位置而進行湊整：（18+22）+（21+19）。

【例5】

[原題 現題 幾次考試中，全班的平均成績都是90分，男生的平均成績是88分，女生的平均成績是95分。已知男生有20人，求女生的人數。 [95分][90分][88分] ]

根據文字信息解答上題，學生理解起來比較困難，但如果將題目以“圖形面積”形式呈現，易于學生理解和解答：男生共20人，由原平均成績88分上升到現在的90分，則總共要增加（90-88）×20=40（分），而這40分是由女生來填補的;女生由原平均成績95分下降到現在的90分，平均每人下降95-90=5（分），則女生有40÷5=8（人）。

【例6】

[原題 現題 有一品牌牛奶，買一盒要4元，買一箱5盒售價15元。小明買4盒，怎樣買合算？寫出你的比較過程 有一品牌牛奶，買一盒要4元，買一箱5盒售價15元。怎樣買合算，請完成下面的表格。

]

買3盒，則單買合算;但買4盒，單買需要16元，而買一箱5盒僅15元，更合算。這是對學生優化思維的一種挑戰，這樣的挑戰也處在三年級學生的最近發展區。

（二）“圖畫—圖形”方式呈現

由直接讀取圖中的數據方式轉化為圖形的數據讀取方式，有助于提高學生對已知信息的獲取和轉換的能力。

【例7】

[原題 現題 左圖是稱西瓜時顯示的質量。請在右圖的秤盤中標出。

]

（三）開放或半開放方式呈現

開放或半開放性的題，可以讓學生不僅“知其然”，更能“知其所以然”。

【例8】

[原題 現題 合理方法計算。

68.5×1.75 + 31[12]×[74] 補充一個數據，使算式簡便。

（? ?）×1.75 + 31[12]×[74] 下圖是長方體的平面展開圖，計算它的體積和表面積。（單位：cm）

下圖是長方體展開圖的四個面，請你先畫出其余兩個面，并量出所需數據，再計算它的體積和表面積。（單位：cm）

]

四、注重習題解法的多樣性

習題不僅要檢測學生能否正確解答，更要檢測學生能否理解和靈活應用數學知識。因此，讓學生多角度去思考問題，尋求不同的解題方法，是教師命題所應追求的目標。

【例9】

A、B兩倉庫共存糧180噸，現從A倉庫運出存糧的[14]，從B倉庫運出存糧的40%，這時A、B兩倉庫剩下的糧食同樣多，A、B兩倉庫原來存糧各多少噸？

此題的解答方法可以多樣化，既能用比例解，也能用方程解，可滿足不同思維方式的學生。

五、關注學科間知識的聯系和整合

在命題中可以把多個科目、多個知識點結合在一起，考核的重點不再是知識點的簡單記憶和重現，而是學生在分析解決實際問題中多方面的學習能力。

【例10】

如果下面的分數中，分子b表示水的量，分母a表示鹽水的總量，那么對于鹽水來說，如果“蒸發”掉一些水m后，它將變得更咸，這個結論可以用數學中的（? ? ?）來解釋。

①? [bab+ma+m]? ③ [ba

【例11】

復式折線統計圖關注的是兩個量之間的比較，學生根據經驗可以判斷實線代表毛衣，虛線代表襯衫。

編制習題時，還可以把數學各領域的知識進行整合，既考查學生對知識的掌握情況，又檢驗學生綜合運用知識的能力，可謂一舉兩得。

【例12】

如右圖，點C、A、E在同一條線段上，線段DE與線段BC平行。問：三角形ABC和直角三角形ADE的面積之和是多少？（單位：分米）

此題考查學生運用旋轉及計算三角形面積的知識。

（浙江省杭州市學軍小學? ?310012）