以數學文化為載體滲透高中數學隱性知識

陳婉清

[摘? ?要]近幾年的數學高考試題多考查學生對知識深層的本質理解，而非表面的理解與復雜的計算。對數學本質的挖掘成為高水平數學教師在數學教學中必須掌握的要點和必須教授給學生的技能。這部分知識往往是課本中沒有具體提及的“隱性知識”。學習數學文化是培養學生數學素養的重要途徑，以“數學文化”為載體滲透高中數學“隱性知識”，不僅可以提高課堂的趣味性，還可以幫助學生更好地了解數學，提升數學素養。文章以人教A版高中數學教材選修2-1中“橢圓”的教學為例，以數學文化為載體，講述高中數學隱性知識。

[關鍵詞]隱性知識;數學文化;圓錐曲線;橢圓

[中圖分類號]? ? G633.6? ? ? ? [文獻標識碼]? ? A? ? ? ? [文章編號]? ? 1674-6058（2019）36-0042-04

一、引言

（一）隱性知識

世界經濟組織（OECD）在《以知識為基礎的經濟》的報告中，將知識分為四類：關于事實的知識（Know-what），關于原理的知識（Know-why），關于如何做好知識（Know-how），關于信息、來源的知識（Know-who）.將前二類稱為顯性知識（explicit knowledge），后二類稱為隱性知識（tact knowledge）.[1]

為了更好地學習隱性知識，相應地把隱性知識分為易于顯性化和不易顯性化兩大類.心理學上已經有證據表明，內隱學習在一定程度上具有可理解特性.[2]這就為隱性知識顯性化提供了理論基礎.

中學數學中的隱性知識包括課本上沒有提及的基本知識;基本思想方法;基本活動經驗及經歷過程中的感受等方面的獲得等.數學教師在教學過程中應充分重視學生對隱性知識的學習，因為，讓學生掌握數學的本質是教學良性發展的保障.

（二）數學文化

“數學文化”一詞的內涵，簡單說，是指數學的思想、精神、方法、觀點以及它們的形成和發展;廣泛些說，除上述內涵以外，還包含數學家、數學史、數學美、數學教育、數學發展中的人文成分、數學與社會的聯系、數學與各種文化的關系等.[3]數學文化無論對于深刻認識作為科學的數學本身，還是全面了解整個人類文明的發展都具有重要意義.

《普通高中數學課程標準（2017年版）》中對高中數學課程性質的定位寫道：“數學承載著思想文化，是人類文明的重要組成部分.”數學文化是在數學知識的發展過程中形成和沉淀的.將“數學文化”這一要素加入中學數學教育教學中，有利于學生更好地了解與理解數學.

關于怎樣“提升學生的數學素養，引導學生學會用數學的眼光觀察世界、用數學思維思考世界、用數學語言表達世界.”這一問題已經成為數學教育行業熱議的問題.在數學課程中“突出數學主線”，凸顯數學的內在邏輯和思想方法;精選課程內容，處理好數學核心素養與知識技能之間的關系，強調數學與生活以及其他學科的聯系，提升學生應用數學解決實際問題的能力.同時注重數學文化的“滲透”，那么，關于“怎樣學好數學”和“數學知識的來源”這兩類屬于數學隱性知識的部分，就可以作為凸顯數學的內在邏輯和思想方法的載體，在數學課程中是必要的，也是非常值得教育工作者進行研究的.

（三）以數學文化為載體，滲透高中數學隱性知識的重要性

一個好的數學教師的標準之一，就是把教材中沒有編寫出來的數學知識（隱性知識）教授給學生，在高中階段以“數學文化”為載體去滲透數學知識，具有很好的可執行性.從學生的角度看，一方面，學生在了解數學知識的形成、發展過程中，可以更透徹地了解所學知識，從而樹立學好數學的信心，喜歡上數學.另一方面，高中作為與大學銜接的階段，數學作為科學的“皇后”，大多數數學知識理論的形成與發展，是在各個學科的發展過程中根據需要逐漸形成的.通過數學文化的滲透，學生可以了解到自己感興趣的地方，進而為繼續學習做好鋪墊.從教師的角度看，一方面，在教學活動過程中，“教什么”要比“怎么教”重要，因為教學內容決定教學形式，教師如果在教學計劃中將教材里的隱性知識同教學內容融會貫通，對于數學教學會是一個質的飛躍.另外，“給學生一杯水，老師要有一桶水”.教師在數學隱性知識顯性化的過程中，自己必然要了解得更多，站在更高的知識角度，盡可能去發掘數學知識中的隱性知識，并且將這些知識以恰當的方式呈現給學生.這對于教師來講，是一個成長過程.另一方面，在課堂中，穿插講授數學文化，可以增強數學課的趣味性，提高課堂教學效率，從而達到事半功倍的效果.

二、教材中與橢圓有關的知識點

本文從人教版A版高中數學教材選修2-1第二章圓錐曲線方程“橢圓”這節內容出發，以從課本中發現本節課存在的“隱性知識”為出發點，以“數學文化”為載體來補充橢圓的教學知識.

（一）教材中的知識安排

從本節人教版教材編寫的順序來看，將“橢圓”安排在選修中，繼必修二學習過在坐標系下建立直線與圓的方程，以及在本章節的第一節研究了一般曲線與方程的關系之后，引入橢圓及其標準方程和其簡單的幾何性質.

教材以一個探究的旁白（如圖1）引入橢圓的第一定義，根據所得的橢圓幾何特征來選擇適當的坐標系，建立橢圓的方程，進而給出了橢圓的標準方程：[x2a2+y2b2=1（a>b>0）]或[y2a2+x2b2=1（a>b>0）].在給出橢圓標準方程后，教材以標準方程：[x2a2+y2b2=1（a>b>0）]為例來研究橢圓的幾何性質.

（二）教材知識內容的局限性

教師設計教學進程，往往逃脫不了教材的限制，可借助多媒體展示天體中行星或者衛星的運動軌跡引入橢圓的概念.通過實驗或課件演示教材中橢圓的形成，將橢圓從現實生活拉到數學世界.接著教師根據教材中所給出來的橢圓的第一定義，引導學生運用第一節所學的求一般曲線的方法來得到橢圓的標準方程，萬變不離其宗.

但從學生對橢圓的理解程度來看，其并沒有很好地理解橢圓的“本質”，只是單純地識記了標準方程[x2a2+y2b2=1（a>b>0）]和一些簡單的性質.2008年，浙江高考理科數學第10題困擾了許多學生，這也說明了學生對橢圓存在著本質上理解的不足.

如圖2，AB是平面[α]的斜線段;A為斜足，若點P在平面[α]內運動，使得[ΔABP]的面積為定值，則動點P的軌跡是（ ）.

解決這道題的關鍵是到直線AB的距離為定值的點的軌跡是圓柱面，而圓柱面被斜平面所截的截線當然是橢圓.這就暴露了教材中沒有明確講出圓錐曲線最初是由圓錐或圓柱的截面得到的，學生頭腦中并沒有將橢圓的生活表象與橢圓的解析幾何表象聯系起來.[4]

三、對“橢圓”中隱性知識的挖掘

（一）隱性知識：圓錐曲線的起源

關于圓錐曲線的起源有兩種說法，一種是在制作日晷中（如圖3所示），隨著太陽的移動，圓形晷盤上晷針影子尖端形成的曲線就是圓錐曲線.另一種說法與“倍立方”問題有關，公元前5世紀，古希臘數學家希波克拉底將“倍立方”問題歸結為求二次比的問題：對一個棱長為[a]的立方體，在[a]和[2a]之間確定[x和y]，使得[a：x=x：y=y：2a].用現在的數學語言來講，就是要同時解下面三個方程中的兩個：[x2=ay，y2=2ax和xy=2a2]，前兩個是拋物線方程，第三個是雙曲線方程.[5]

圓錐曲線出現在公元前4世紀，柏拉圖學派的梅內克繆斯在解決“倍立方”問題時研究了圓錐曲線的性質.他用垂直于母線的平面去截頂角分別為銳角、直角和鈍角的正圓錐，得到橢圓、拋物線和雙曲線的一支（如圖4所示）.

再來看教材章節開頭目錄中的圖片（如圖5所示），這其實就是阿波羅尼斯（Apollonius，約公元前262-公元前190）所定義的圓錐曲線，他將圓錐曲線定義為：用一個平面去截一個圓錐面，得到的交線就稱為圓錐曲線.在他的著作《圓錐曲線論》中，圓錐曲線也稱為“圓錐截線”，嚴格來講，被截的圓錐面有正圓錐面或斜圓錐面，得到的交線除了圓、橢圓、雙曲線和拋物線外，還包含三種退化情形（一條直線、一個點、兩條相交直線）.

關于阿波羅尼斯，他是第一個依據同一個（正的或是斜的）圓錐的截面來研究圓錐曲線理論的人，也是第一個發現雙曲線有兩支的人.其所著的《圓錐曲線論》（Conic Sections）共八篇，最后一篇已失傳.前三篇主要是歐幾里得關于圓錐曲線的失傳著作的內容，包括梅內克繆斯（Menaechmus，約公元前380-公元前320）和阿基米德（Archimedes，公元前287-公元前212）在這方面的工作.阿波羅尼斯在前人的基礎上去粗取精，按照歐幾里得《幾何原本》公理演繹的方式組織內容，使知識系統化.《圓錐曲線論》含有許多獨到和新穎的創造性材料，幾乎網羅了圓錐曲線的性質.阿波羅尼斯將歐幾里得的幾何論證水平發展到極致，使《圓錐曲線論》成為數學史上的一座豐碑，他本人也被稱為古希臘“偉大的幾何學家”.[6]

在此之后，古希臘后期的數學家帕普斯（Pappus，公元3世紀末）在他的《數學匯編》中證明了橢圓、雙曲線和拋物線的焦點-準線性質：到一定點（焦點）及定直線（準線）的距離成一定比例的一切點的軌跡是一圓錐曲線.[5]即我們現在說的圓錐曲線的第二定義或統一定義.

（二）橢圓及其標準方程

1.橢圓定義中的隱性知識

教材中所給的探究旁白中的作圖方法其實是16世紀初，意大利數學家蒙特與后來的荷蘭數學家舒騰所做橢圓的方法.在這一階段，人們認識到圓錐曲線并不只是依附在圓錐面上的靜態曲線，也是自然界物體運動的普遍形式.德國天文學家開普勒（Johannes Kepler，1571-1630）揭示出行星按橢圓軌道環繞太陽運行，并發現了圓錐曲線的焦點和離心率.[7]在這段時期里，坐標系與解析幾何并未出現.

17世紀解析幾何出現之后，法國數學家洛必達拋棄了古希臘人的定義方法，將橢圓定義為在平面上到兩定點距離之和等于常數的動點軌跡（也就是教材中的橢圓定義），并據此推導出了橢圓方程.

2.橢圓的標準方程中的隱性知識

教材中所給出的橢圓標準方程的推導是基于坐標系下的推導方法.而在對橢圓方程的探究過程中，許多數學愛好者給出了更為自然的推導方法，我們有必要對其進行了解.

（1）教材中橢圓標準方程的推導

根據橢圓的幾何特征，類比利用圓的對稱性建立圓的方程的過程.選擇適當的坐標系，建立橢圓方程.

（2）橢圓方程推導中的隱性知識：橢圓發展過程中的四種推導方法

①余弦定理推導方法

如圖6所示，設[PF2=z]，因為[PF1+PF2=2a]，所以[PF1=2a-z].

由余弦定理得[（2a-z）2=z2+4c2-4czcosθ=z2+4c2-4c（c-x）].

解得：[z=a2-cxa]

由勾股定理得[z2=a4-2a2cx+c2x2a2=y2+（c-x）2]

整理得[a2y2+b2x2=a2b2]即[x2a2+y2b2=1].

②利用橢圓第二定義進行推導——離心率

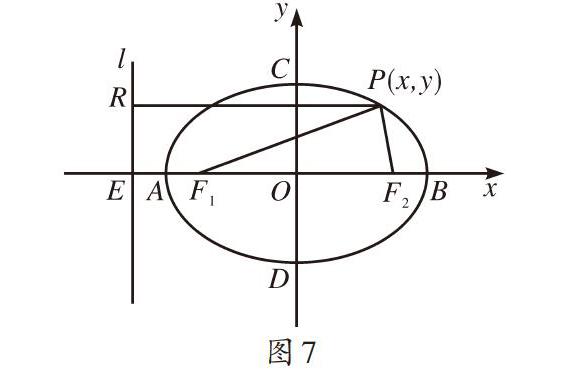
如圖7所示，設[PF1PR=AF1AE=BF1BE=e]，[AB=2a]，[EO=ae]，[F1F2=2ae]，點[P（x，y）]的坐標滿足[PF12=e2PR2][（ae+x）2+y2=e2ae+x2]，整理得[x2a2+y2a2（1-e2）=1]，記[b2=a2（1-e2）]即得[x2a2+y2b2=1].

3.橢圓簡單幾何性質中的隱性知識

在這一塊講到橢圓的離心率——我們把橢圓的焦距與長軸長的比[ca]稱為橢圓的離心率，用[e]表示時，結合探究旁白中“[ba]與[cb]的大小能刻畫橢圓的扁平程度嗎？為什么？”來思考為什么要用[e=ca]來表示橢圓的離心率.

對于這個問題，[ba]與[cb]的大小可以用來刻畫橢圓的扁平程度，但相對于[ba]與[cb]來說，[ca]更具有優勢.我們知道橢圓是平面內到兩定點的距離值和為常數的點的軌跡.第二定義中涉及的參數是[a]和[c]，為了保持一致，用[ca]來表示橢圓的離心率.

另外，圓錐曲線的統一定義為：“到定點距離與到直線距離之比為常數”，而這個常數的值恰好是[ca]，所以用[ca]表示離心率更具有統一性.

4.教材例題中存在的隱性知識

在講述完本節課知識點后，教材中例5的設計隱含了橢圓的光學性質（是指由橢圓一焦點射出的光線經過橢圓內壁反射后，必經過另一焦點，其等價于：橢圓上任意點的切線與兩焦半徑所成夾角相同），例6隱含了橢圓的第二定義.教師在講例題的過程中，可以結合例題，將題后所隱含的知識講給學生聽，為學生在接下來練習過程中思路的開拓奠定基礎.

5.“橢圓”知識體系中隱含的數學思想方法

高水平教師在教學活動中往往會對教學內容進行“點睛”——結合教學內容體現相應的數學思想方法.在“橢圓”的教學過程中，體現了分類與整合思想、函數方程思想、數形結合思想以及轉化思想.在教學過程中進行數學思想方法隱性知識的滲透，無疑可以幫助學生更好地掌握知識的本質，學好數學.

四、小結

綜合來講，從教材中發現數學隱性知識，以“數學文化”為載體對教材中的隱性知識進行挖掘，可以對教材中知識講授的順序做一個“發生過程”的補充，使知識看起來更為連貫，學生接受起來也沒有那么生硬.高水平的教師，能夠透過現象看到本質，在教授教材中顯性知識的同時，能挖掘出其后的隱性知識.此時，教師的身上自然散發著一種獨特的數學光華與氣息，攜自身的全部數學涵養融入教室，融入課堂，融入學生，學生由此汲取數學的豐富營養.[8]

[? 參? ?考? ?文? ?獻? ]

[1]? 陳淑彬.隱性知識顯性化在數學教學中的作用[J].科技信息，2009（21）：637.

[2]? 高湘萍.隱性知識的獲得及其顯性化的心理途徑[J].全球教育展望，2003（8）：27-29.

[3]? 顧沛.數學文化[M].北京：高等教育出版社，2008.

[4]? 王芳，汪曉勤.HPM視角下橢圓概念教學的意義[J].中學數學月刊，2012（4）：57-60.

[5]? 鄒佳晨. 橢圓的歷史與教學[D].上海：華東師范大學，2010.

[6]? 王海青，李曉波.從阿波羅尼斯到柯西：“圓錐曲線”研究方法的變遷[J].數學通報，2018（10）：26-31.

[7]? 汪曉勤.橢圓方程之旅[J].數學通報，2013（4）：52-56.

[8]? 李祎.高水平數學教學到底該教什么[J].數學教育學報，2014（6）：31-35.

（責任編輯 斯? ?陌）