以變顯質，談初中數學的變式訓練

姜煒

[摘? 要] 變式訓練是將知識轉化成技能的一個重要途徑. 在初中數學學習中，應用變式訓練，既能從“變”中突顯數學知識的本質，又在培養學生數學邏輯思維、創新思維等方面有著積極且重要的作用. 文章結合教學實例，對初中數學變式訓練的有效實踐進行了深入解析.

[關鍵詞] 初中數學;變式訓練;思維;實踐

“熟能生巧”是中國傳統教育理念，它在數學教學中的應用尤為突出，國際教育界對于數學練習的重要性，認識度也在提高. 做一定的練習在數學學習中是很有必要的，國內外數學教育者對此已經達成共識. 如何避免題海戰術，使數學練習達到事半功倍的效果？如何讓數學題發揮更好的訓練思維的作用？筆者認為，通過變式訓練的方法，即將類型相同的題目，換個數據或者角度，來考查相似領域或者其他領域的數學問題，“變著花樣”進行練習，既能避免學生因反復操練而形成抵觸心理，又能加深學生們對數學本質的認識和理解，特別地，它更是對學生進行思維訓練的一種最佳方法. 基于此，筆者從教學實踐出發，對變式訓練應如何應用于初中數學教學進行了詳細闡述.

注重變式訓練的“選題”

數學教師在對學生進行變式訓練時，首先要注意的就是“選題”. 所選練習題應該是較為典型的，其中包含較多知識點的代表性題型，不能太過簡單也不能太過復雜，既要能引起學生們挑戰“不可能”的興趣和心理，也要能夠激發他們積極探究的熱情，同時還要能夠在一定程度上幫助學生打破思維定式，形成發散思維.

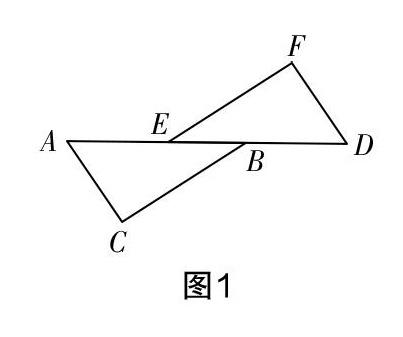
例1如圖1所示，AE=DB，∠A=∠D，∠C=∠F，證明：AC=DF.

變式1如圖1所示，AE=DB，∠A=∠D，AC=DF，求證：（1）BC=EF;（2）BC∥EF.

[圖1]

變式2如圖1所示，∠C=∠F ，AC=DF，請再添加一個條件，使△ACB≌△DFE.

變式3如圖1所示，BC=EF，AC=DF，BC∥EF，△ACB與△DFE是否全等？如果全等，請說明理由;如果不全等，請畫出反例.

“全等三角形”這一章，學生剛剛接觸幾何證明不久，在學習了全等三角形的判定定理之后，這樣的變式練習能夠幫助他們復習所學知識，同時鍛煉幾何證明題的思維方式，讓他們對于怎樣通過證明三角形全等證明線段或者角相等，甚至兩直線平行，有自己的認識. “變式1”并不難，基礎知識掌握得比較扎實的學生都可以輕松完成. “變式2”較開放，通過讓學生思考所有添加條件的可能性，可以對所學的幾種三角形全等判定定理進行梳理復習，形成系統的知識體系. 同時，也通過學生自己說條件，進一步熟悉幾何語言. “變式3”是對“邊邊角”這一易錯點進行辨析. 題后可以進一步引發學生思考：“在已知條件的基礎上，能否再添加一個條件，使得△ACB與△DFE全等？”事實上，若使∠ABC=∠FED=90°，則可用“HL”判定△ACB≌△DFE，從而引導學生對“HL”有更深刻的認識. 我們還可以繼續讓學生思考變式：“若∠ABC=∠FED>90°，△ACB與△DFE是否全等？”“∠ABC還要滿足什么條件，就可以使△ACB≌△DFE？”這兩個變式的要求相對較高，有利于學生思維的進一步提升. 如此一來，由一題引發多個變式，層層遞進，能滿足各個層次學生的需求，并且可以讓學生看到因小小的變化而產生千變萬化的圖形，從而使學生認識數學的美，對數學給予更多關注，從而在變化中逐漸養成多視角看問題、解決問題的意識. 尤其是這樣的變式訓練，通過對題目進行適當處理，能加強知識橫向與縱向之間的聯系，對中學生構建完整的數學知識體系大有裨益.

注重“發散思維”的培養

發散思維是在來源相同的材料中尋找不同答案的一種思維方式和思維過程，這種思維的特征是更變通、流暢和具有創造性. 它表現為思維視野廣闊，思維呈現出多維發散狀. 從心理學角度來說，人的創造力與其發散思維是密切相關的，它們之間存在著正比例關系. 數學素有“思維體操”之稱，要在數學教學中培養學生的發散思維，變式訓練無疑是最好的一個途徑.

如學習“平面直角坐標系”時，我們對點的坐標進行變換：點A（a，b）向左平移m個單位長度后得到的點的坐標為______. 做完之后我們可以讓學生自己對點的坐標進行變換編題，此時學生較易想到，點同樣可以向右、向上、向下平移，從而找到變化規律. 之后我們進一步啟發學生，圖形除了平移之外，還有哪些變化？學生能夠聯想到圖形的翻折、旋轉，從而引導學生自己提出并且探究下列問題：點A（a，b）關于x軸對稱的點的坐標為______;點A（a，b）關于y軸對稱的點的坐標為______;點A（a，b）繞原點旋轉180°后得到的點的坐標為______. 再由特殊到一般，繼續引導學生發現問題并研究下列問題：點A（a，b）關于直線x=m對稱的點的坐標為______;點A（a，b）關于直線y=n對稱的點的坐標為______;點A（a，b）繞原點順時針旋轉90°后得到的點的坐標為______;點A（a，b）繞原點逆時針旋轉90°后得到的點的坐標為__________;點A（a，b）繞點B（c，d）旋轉180°后得到的點的坐標為______.

很明顯，這樣的變式訓練能讓學生自己提出問題探究，學生的思維更加活躍，探究也更熱烈和深入. 學生在練習時能逐漸學會如何創造性地分析問題、解決問題，也能在這種創造性思維中對數學知識的本質有更深入的理解.

注重變式訓練的“變化方向”

變式訓練的核心在于一個“變”字，那么應該怎么變才能達到預期的效果呢？筆者以兩個幾何題為例，對變式訓練應圍繞哪幾個“方向”著手設計進行了詳細闡述.

1. 變內容

巧妙的變化一下提問內容，給學生制造一定的難度，對學生的數學思維是很好的.

例2如圖2所示，點E，F是正方形ABCD的邊BC，CD上的點，且AE⊥BF，求證：AE=BF.

（對于本題，學生根據全等能夠很容易地證出來）

變式1如圖3所示，M，N，P，Q分別是正方形ABCD的邊AB，BC，CD，DA上的點，且MP⊥NQ. 求證：MP=NQ.

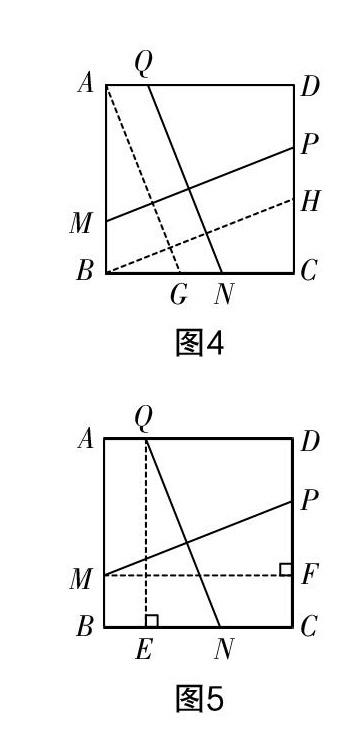
這里，正方形內部兩條互相垂直的線段的位置發生了改變，我們可以平移MP與NQ的位置，得到與例2相同的圖形（如圖4所示），也可以通過作垂線構造全等三角形來解決（如圖5所示），其本質是一樣的，都是通過添加輔助線構造了全等三角形，體現了幾何問題中用三角形解決問題的思想.

變式2如圖6所示，正方形ABCD的邊長為12，將正方形折疊，使頂點A與BC邊上的點E重合，且BE=5，折痕交AB于點P，交CD于點Q，求折痕PQ的長度.

這個問題學生一開始思考起來比較困難，但如果充分運用折疊條件，便會發現點A與點E關于線段PQ對稱，那么連接AE（如圖7所示），便能得到PQ垂直平分AE，與例2類似，我們便可以證得AE=PQ. 要求PQ的長度，只需要在Rt△ABE中求出AE的長度即可. 此題雖然與前兩題看著不同，但是其實是上兩題基本圖形的延伸.

2. 變條件

如將例2變式2的已知條件與所求進行交換：如圖6所示，折疊正方形ABCD，使頂點A與BC邊上的點E重合，且BE=3，折痕交AB于點P，交CD于點Q，DQ=2，求正方形ABCD的邊長.

當學生掌握了某類型題的基本解題方法后，就要通過變式訓練強化他們對問題本質的深入理解，通過變條件的方法，讓他們學會如何“抵抗”因條件變化而產生的信息干擾. 上題依然是利用構造全等三角形來解決的.

例3如圖8所示，四邊形ABCD是正方形，E是邊BC的中點，∠AEF=90°，且EF交正方形的外角∠DCG的平分線CF于點F. 求證：AE=EF.

學生解決本題時往往第一反應是過點F向BG作垂線段，但是會發現無法證出結論. 經過分析，取AB的中點H（如圖9所示），可構造出△AHE≌△ECF，從而得證.

變式將例3中的點E改為BC邊上的任意一點（如圖10所示），從特殊到一般來探索問題的本質，學生會發現，其實例3取AB的中點是構造了等腰直角三角形HBE，因此我們解決本題時在AB上截取BM=BE（如圖11所示），通過構造等腰直角三角形HBE，依然可以得到△AME≌△ECF.

在這樣的變式訓練和有效引導中，又回歸到數學原理的本質中來. 一旦學生通過這樣的訓練突破了思維瓶頸，思維領域就會變得更寬、更廣.

變式訓練對于學生而言，最直接的效果就是會讓他們認識到數學并不難學，數學題并不難做，只要掌握了變化的規律和技巧，于變式之中找到數學最本質、最核心的思想，“以不變應萬變”，一切問題都會迎刃而解.