柔性關(guān)節(jié)柔性連桿機械臂抑振軌跡規(guī)劃

王 航

(西安鐵路職業(yè)技術(shù)學院機電工程學院，陜西 西安 710026)

相比于一般的工業(yè)機器人，柔性機械臂的材質(zhì)密度小，可以較低的能耗、較短的時間使機械臂工具端達到目標地點并盡快趨于穩(wěn)定。柔性機械臂在運動過程中易產(chǎn)生彈性振動，這將導致機械臂工具端的定位精度下降，甚至導致系統(tǒng)失穩(wěn)，且在機械臂關(guān)節(jié)處存在著傳動、減速裝置，這些設(shè)備不可避免地存在柔性，關(guān)節(jié)柔性的存在會使機械臂在運動停止后產(chǎn)生殘余振動，需要對全柔性機械臂進行振動抑制研究。

關(guān)節(jié)柔性和連桿柔性的機械臂是全柔性機械臂。柔性機械臂振動抑制的研究主要集中在控制算法和軌跡規(guī)劃兩個方面。文獻[1]首先采用五次多項式函數(shù)對末端軌跡進行插值，將滿足機械臂末端振動最小化的軌跡規(guī)劃問題轉(zhuǎn)換為待定冗余參數(shù)的優(yōu)化問題，然后采用粒子群優(yōu)化算法求解該組參數(shù)。文獻[2]采用正弦-梯形函數(shù)作為各關(guān)節(jié)的角速度函數(shù)，優(yōu)化了其中的系數(shù)和幅值參數(shù)。文獻[3]采用五次多項式函數(shù)作為關(guān)節(jié)空間插值函數(shù)，以軌跡控制點的位移浮動值作為待優(yōu)化變量，使用遺傳算法優(yōu)化得到柔性臂振動能量最小的最優(yōu)抑振軌跡。文獻[4]使用改進PSO算法，以激振力為性能指標對B樣條軌跡進行優(yōu)化。文獻[5]建立剛?cè)狁詈蠙C械臂時考慮了柔性臂桿的大變形，使用粒子群優(yōu)化算法確定了最優(yōu)軌跡的插值點的波動量。文獻[6]提出的目標函數(shù)分別是機械臂的能耗和殘余振動，使用多目標遺傳算法獲得最優(yōu)多項式軌跡的系數(shù)。文獻[7]針對一種專用高速動作的微型機械臂，建立了以力矩和振動為優(yōu)化指標的目標函數(shù)。文獻[8]研究了關(guān)節(jié)軌跡插值函數(shù)是擺線方程的優(yōu)化問題。

機械臂軌跡規(guī)劃方面的研究成果豐碩，但與柔性機械臂振動抑制軌跡規(guī)劃有關(guān)的文獻就相對有限，可以考慮將剛性機械臂臂軌跡規(guī)劃方面的研究成果應(yīng)用到柔性機械臂。一般而言，柔性機械臂的軌跡規(guī)劃曲線多為多項式曲線，而多種曲線組合的形式不多見，因此有必要開展這方面的研究工作。

1 柔性關(guān)節(jié)柔性機械臂的動力學建模

機械臂由多個臂桿鉸接在一起構(gòu)成[9]。在機械臂的連桿中,有些是短而粗的，可忽略柔性視其為剛體；而另一些細而長的，其彈性變形不可忽略[10]。文獻[11]指出，機械臂關(guān)節(jié)的柔性源自諧波減速器和力矩傳感器。

就理論研究而言，軌跡規(guī)劃的前提是建立柔性機械臂的動力學方程。柔性臂桿的建模一般采用假設(shè)模態(tài)法，而柔性關(guān)節(jié)的建模通常采用的是Spong模型[12]。全柔性機械臂的簡圖如圖1所示。

1.1 動力學方程

本文采用Lagrange法建立動力學模型。不考慮連桿的端部質(zhì)量，則系統(tǒng)的動能包含關(guān)節(jié)驅(qū)動裝置動能和柔性桿動能，系統(tǒng)的勢能包含柔性臂桿的彈性勢能和柔性關(guān)節(jié)的彈性勢能。

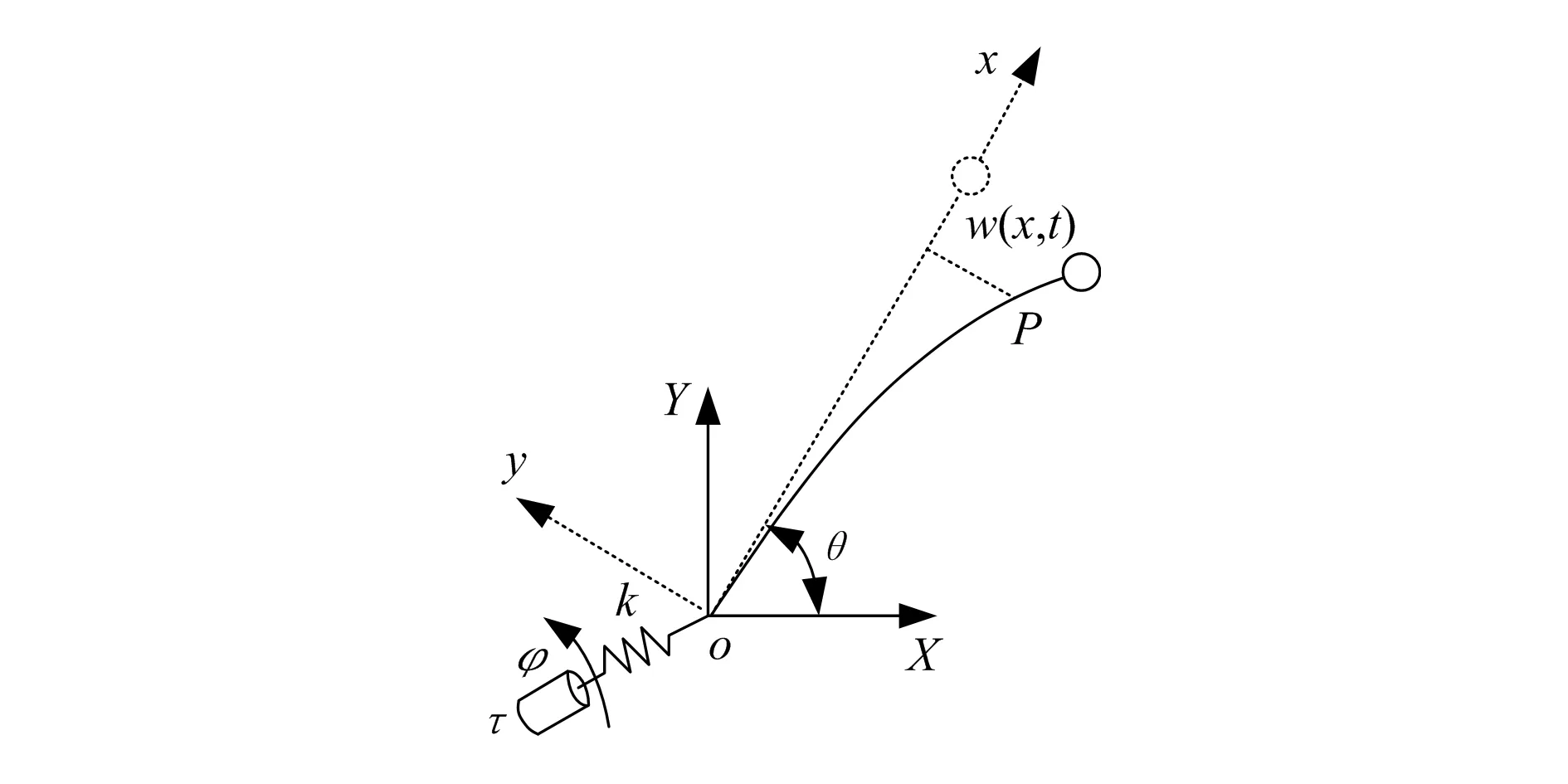
圖1 單臂全柔性機械臂

在圖1中，桿臂為柔性桿，關(guān)節(jié)為柔性關(guān)節(jié)。在某個瞬時，柔性桿上任意一點P的橫變形用w表示，則w是坐標x和時間t的函數(shù)，記為w(x,t)，設(shè)笛卡爾坐標系o-XY為該系統(tǒng)的基礎(chǔ)坐標系，o-xy為附體坐標系。圖中，τ為關(guān)節(jié)處的驅(qū)動力矩，θ為柔性連桿關(guān)節(jié)轉(zhuǎn)角，φ為驅(qū)動裝置轉(zhuǎn)角，k為柔性關(guān)節(jié)等效剛度。此外，設(shè)L為柔性連桿未變形的長度，m為柔性連桿的質(zhì)量。

某時刻P點坐標可以表示為

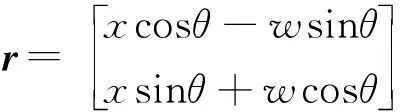
(1)

將r對t求導，可得P點的瞬時速度。

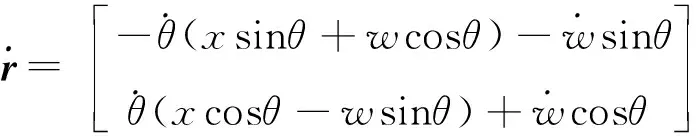
(2)

則柔性關(guān)節(jié)柔性連桿機械臂的動能T表示為：

(3)

式中：J1為驅(qū)動裝置的轉(zhuǎn)動慣量；J2為關(guān)節(jié)處傳動設(shè)備的轉(zhuǎn)動慣量；ρ為密度；A為桿的截面積。

不計重力，則機械臂的勢能U只是柔性臂的彈性勢能，表達式如下：

(4)

式中：E為彈性模量；I為截面慣性矩。

將T,U代入Lagrange方程，得

(5)

式中：q為系統(tǒng)廣義坐標；Q為系統(tǒng)廣義力矩陣，Q=[τ,0,0,0]。

由均勻等截面Euler-Bernoulli梁理論振動微分方程，可得梁的彈性變形的表達式為[13]：

(6)

式中：φi(x)為柔性桿的第i階振型函數(shù)；ai(t)為與振型函數(shù)相對應(yīng)的模態(tài)坐標。

采用懸臂梁振動模態(tài)，并取二階模態(tài)，代入式(5)，得動力學方程為,

(7)

式中：M,K分別為質(zhì)量、剛度矩陣。此時廣義坐標q=[φ,θ,a1,a2]。

1.2 運動與振動的關(guān)系

系統(tǒng)動力學方程式表明柔性關(guān)節(jié)柔性連桿機械臂關(guān)節(jié)和桿臂具有耦合的特性。將動力學方程中與廣義力矩相關(guān)的項略去，即可得到用于柔性臂抑振軌跡規(guī)劃的動力學方程：

(8)

式(8)表達了傳動裝置轉(zhuǎn)角、關(guān)節(jié)運動與模態(tài)坐標之間的關(guān)系，對其進行求解可得出機械臂傳動裝置軌跡對機械臂結(jié)構(gòu)振動影響的情況。

2 最優(yōu)軌跡規(guī)劃

2.1 三次樣條曲線

軌跡規(guī)劃的中心任務(wù)是選取關(guān)節(jié)空間的插值曲線。三次樣條曲線不能保證端點處的速度、加速度同時為零，故首末兩段曲線使用多項式曲線連接。

將柔性臂運動時間歷程等分為n個相等的時間間隔，時間節(jié)點依次為t1,t2,t3,…,tn。時間節(jié)點ti對應(yīng)的柔性臂角位移為θi。使θi值增減給定的區(qū)間范圍內(nèi)的一個變化值，進而得到不同的軌跡控制點下的位移曲線。

插值點縱坐標的表達式為：

θ1i=θi+Δθi

(9)

式中：θ1i為插值點縱坐標值；θi為基礎(chǔ)插值點值；Δθi為坐標變化值。角位移曲線如圖2所示。

本文中所使用的插值曲線建立方式參考文獻[14]。其中首尾兩段五次多項式表示如下：

q1(t)=a0(t-t1)3(t-t0)2

(10)

qn(t)=an-1(t-tn-1)3(t-tn)2

(11)

圖2 插值點處的變化量

2.2 目標函數(shù)

一般而言，在[0,tf]的時間段內(nèi)機械臂被驅(qū)動，在[tf,2tf]時間段內(nèi)停止驅(qū)動機械臂，在該段時間內(nèi)可考察機械臂的殘余振動，其中tf為機械臂的運動時間。將關(guān)節(jié)空間插值求得的驅(qū)動裝置轉(zhuǎn)角代入式(8)即可得到柔性臂桿的轉(zhuǎn)角、一階模態(tài)坐標和二階模態(tài)坐標的值。

柔性臂桿的殘余振動是指臂桿在運動結(jié)束后末端撓度的最大值f1。

f1=max|φ1(L)a1(t)+φ2(L)a2(t)|

(12)

式中：φ1(L)，φ2(L)分別為懸臂梁取L第1，2階振型函數(shù)的值，a1(t)，a2(t)為對應(yīng)的模態(tài)坐標。

柔性關(guān)節(jié)的殘余振動是指運動結(jié)束后臂桿的角位移與驅(qū)動裝置角位移差值的最大值f2：

f2=max|φ(t)-θ(t)|tf≤t≤2tf

(13)

本文采用加權(quán)系數(shù)法將兩個目標函數(shù)整合在一起。加權(quán)系數(shù)的引入是因為柔性臂桿的殘余振動與關(guān)節(jié)柔性引起的殘余振動之間存在差異，需要反復試算才能確定加權(quán)系數(shù)。總的目標函數(shù)如下所示。

f=αf1+f2tf≤t≤2tf

(14)

式中：α為加權(quán)系數(shù)。則該優(yōu)化問題的目標函數(shù)可寫為

minf

s.t.Δθi∈(-0.1|θn-θi|,0.1|θn-θi|)

i=1,2,…,n

(15)

2.3 免疫遺傳算法

免疫遺傳算法是將免疫思想和遺傳算法相結(jié)合而發(fā)展起來的一種群智能優(yōu)化算法[15]。免疫遺傳算法的興起較遺傳算法晚，因此可以視為遺傳算法的一種衍生算法。與遺傳算法相比，免疫遺傳算法不需雜交操作，而是采用注入疫苗的方法。疫苗是優(yōu)秀染色體中的一段基因，注入疫苗是指把疫苗接種到其他染色體中。對于絕大多數(shù)的優(yōu)化問題而言，遺傳算法和免疫遺傳算法的尋優(yōu)結(jié)果并沒有優(yōu)劣之分，計算效率相差不大。但免疫遺傳算法的出現(xiàn)為群智能算法開辟了新的領(lǐng)域。

免疫遺傳算法流程如下：

1)產(chǎn)生初始抗體群。隨機產(chǎn)生N個個體，并從中提取m個個體構(gòu)成初始群體，稱其為記憶庫，其中m為記憶庫中個體的數(shù)量。

2)計算適應(yīng)度，并完成種群中各個抗體的評價。

3)形成父代群體。將初始群體按期望繁殖率進行降序排列，并取前N個個體構(gòu)成父代群體，同時取前m個個體存入記憶庫中。

4)判斷是否達到結(jié)束的次數(shù),是則結(jié)束；反之則繼續(xù)下一步操作。

5)產(chǎn)生新種群。在步驟3)的計算結(jié)果基礎(chǔ)上對抗體群體進行選擇、交叉、變異操作得到新群體，并與記憶庫中的個體共同構(gòu)成新一代群體。

6)執(zhí)行步驟2)。

3 數(shù)值計算

3.1 參數(shù)設(shè)置

機械臂的相關(guān)參數(shù)設(shè)置均參考文獻[11]，因此本節(jié)得到的計算結(jié)果對空間機械臂的抑振軌跡規(guī)劃有一定的意義，同時對于SCARA等平面二關(guān)節(jié)機器人亦有相似的參考價值。具體而言，桿長L為0.75m，臂桿線密度ρ為3.74kg/m，柔性臂抗彎剛度EI為23.625N·m2，傳動裝置剛度k為200。反復試算可知，目標函數(shù)的值在計算過程中的變動量較大，但是數(shù)量級相差不大，取加權(quán)系數(shù)α=1×10-1，則目標函數(shù)的值將不存在數(shù)量級的差異，各部分的值均在目標函數(shù)中有所體現(xiàn)。為了凸顯軌跡規(guī)劃的有效性，設(shè)置機械臂在較短的時間完成較長的軌跡，參考文獻[3]，機械臂的運動時間tf=2s。免疫遺傳算法的參數(shù)設(shè)置為：種群規(guī)模100，交叉率0.7，變異率0.02，迭代次數(shù)100。微分方程的求解采用定步長四階龍哥庫塔法，步長為0.001s，三次樣條的求解采用追趕法。

3.2 仿真結(jié)果

采用配備第7代酷睿i5處理器的聯(lián)想微機。計算的總時長為6 391s。仿真過程中注意到，自變量取值范圍的系數(shù)參考文獻[5]時，計算的過程中會出現(xiàn)奇異解，在變量范圍選取時應(yīng)當注意這一點。

由圖3可知，最優(yōu)目標函數(shù)值在50次迭代之后即趨于穩(wěn)定。在計算的前期目標函數(shù)有波動，隨著計算的進行，目標函數(shù)迅速減小并趨于穩(wěn)定。得到一組最優(yōu)解x=[-0.067 00 0.009 68 -0.077 10 -0.077 50 -0.095 40 -0.094 30 -0.034 50 -0.037 90 0.073 20]。

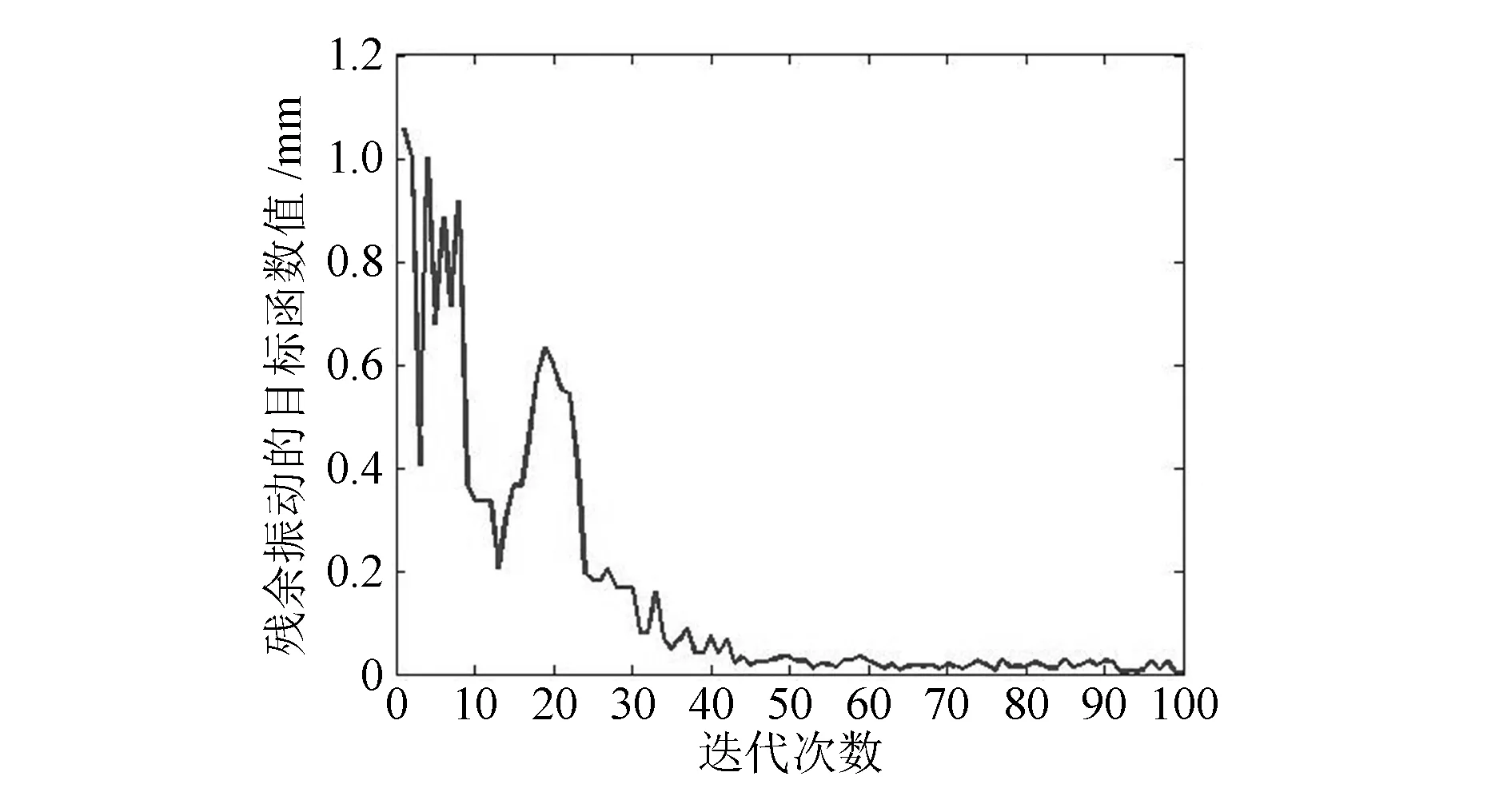
圖3 優(yōu)化計算過程

圖4所示為優(yōu)化后驅(qū)動裝置角位移曲線，曲線平滑。圖5，6所示分別為優(yōu)化后角速度、角加速度曲線。由圖可知，采用分段的方式使得初始和終止位置的速度、加速度為零，而且插值點處的角速度、角加速度曲線過渡平緩，最值較小。

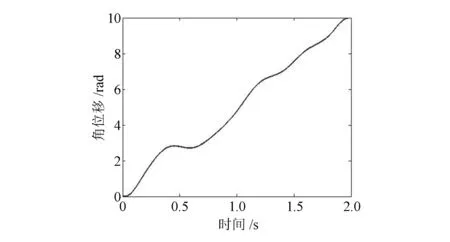
圖4 優(yōu)化后的插值曲線

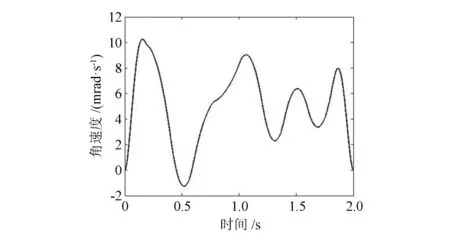
圖5 優(yōu)化后角速度曲線

圖7所示是柔性關(guān)節(jié)的殘余振動曲線，圖8所示是柔性臂桿末端的殘余振動曲線。2個圖中，前2s是機械臂受到驅(qū)動的運動曲線，后2s不驅(qū)動機械臂，用于研究殘余振動。比較兩條曲線可知，優(yōu)化后機械臂的關(guān)節(jié)殘余振動和柔性臂桿末端的殘余振動均顯著減小。關(guān)節(jié)變形由0.057 7減小為0.000 1，臂桿殘余振動由0.012 0減小為0.000 1。優(yōu)化后，柔性關(guān)節(jié)的運動曲線變得平滑。這里只考慮了機械臂的殘余振動，機械臂運動過程中的振動不在考慮范圍內(nèi)。圖像中也顯示出了類似的結(jié)果，即運動過程中的彈性變形并沒有因為良好的軌跡規(guī)劃而顯示出較好的動態(tài)特性。

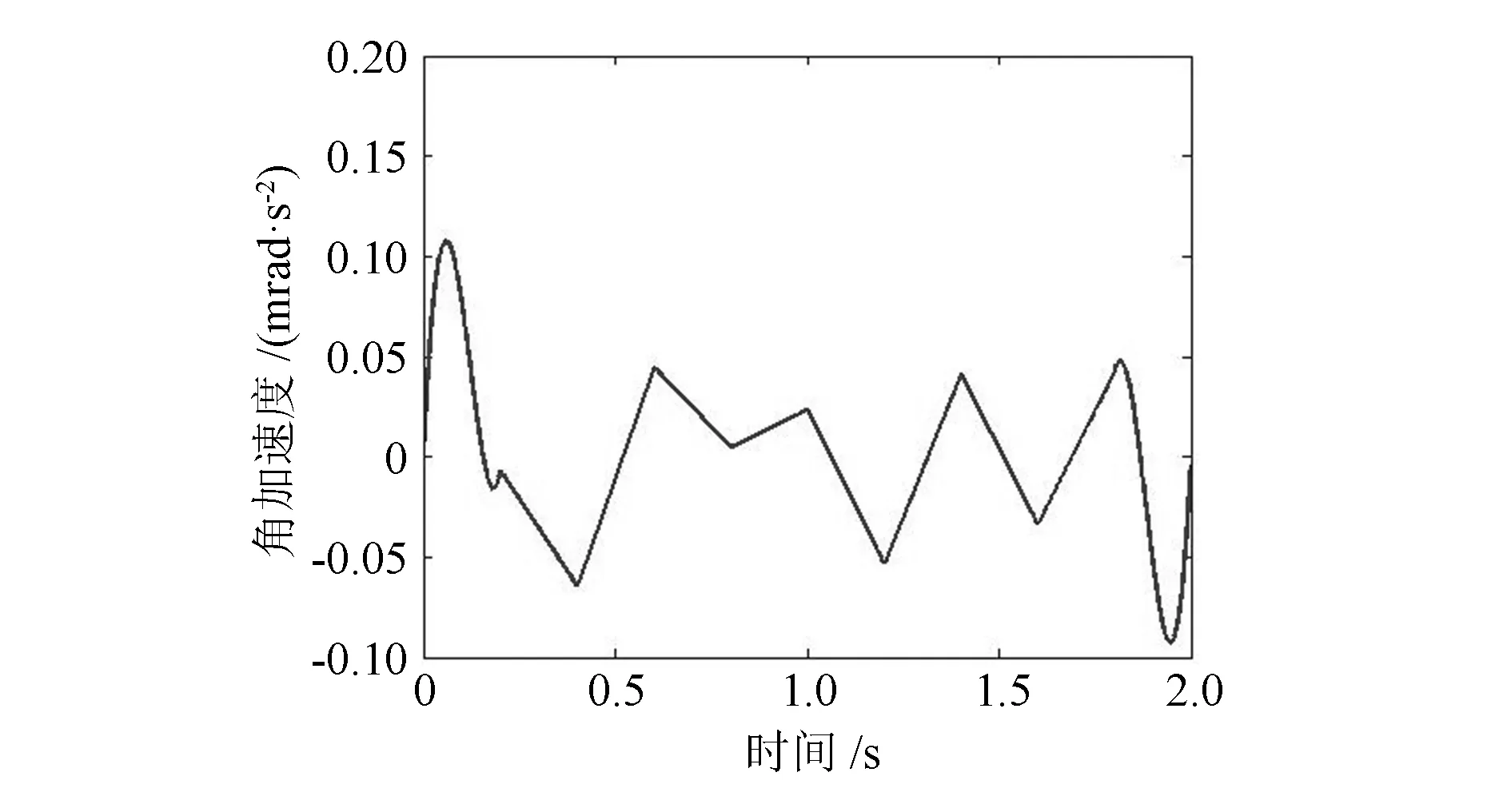
圖6 優(yōu)化后角加速度曲線

圖7 關(guān)節(jié)殘余振動曲線

圖8 柔性桿末端殘余振動曲線

4 結(jié)束語

本文對單連桿全柔性機器人振動抑制的研究側(cè)重于理論方面。采用三次樣條曲線和五次多項式組合的方式進行軌跡插值的方法對多連桿柔性機械臂同樣適用，但需要相關(guān)實驗驗證本文方法的有效性，因而后續(xù)的研究應(yīng)與實驗結(jié)合起來。