帶有安裝時間與維修活動的單機排序問題
趙玉芳, 葛秋利
(沈陽師范大學 數學與系統科學學院, 沈陽 110034)
0 引 言
生活中,帶有維修和交貨期窗口的問題受到了廣泛的關注,具有重要的實際意義[1]。在某些情況下,在工件加工之前需要有安裝時間,在加工過程中通過維修活動可以使機器的生產效率提高。Mor和Mosheiov[1]研究了帶有交貨期窗口和維修的單機排序問題;Wang等[2]研究了帶有學習效應、退化效應和交貨期窗口的單機排序問題;Cheng等[3]研究了維修時間與開始時間相關的帶有退化效應和交貨期窗口的單機排序問題;Janiak等[4]總結了關于交貨期窗口的研究進展;王吉波等[5]討論了同時具有學習和惡化效應的不同工期指派問題,并給出了多項式算法。
在帶有安裝時間的模型中,Koulamas和Kyparisis[6]提出了線性和非線性的安裝時間模型,討論了目標函數分別為最大完工時間、總完工時間及總完工時間的絕對差之和的單機排序問題,給出了計算復雜性都為O(nlogn)的多項式最優算法;Kuo和Yang[7]研究了帶有安裝時間和學習效應的單機排序問題;Wang等[8]研究了帶有安裝時間和學習效應與退化效應的單機排序問題;Huang等[9]討論了帶有安裝時間、與位置有關的學習效應和退化效應的單機排序問題;Lee[10]討論了帶有安裝時間與學習效應和退化效應的單機排序問題;關于帶有交貨期窗口和維修的問題,Mosheiov和Oron[11]研究了帶有交貨期窗口的單機排序問題,給出了計算復雜性為O(nlogn)多項式算法,對于加工時間與位置相關的帶有交貨期窗口的單機排序問題,給出了計算復雜性為O(n3)多項式算法;Wu和Ji[12]對于加工時間分別具有退化效應與學習效應的含有交貨期窗口的單機排序問題進行了研究,給出了計算復雜性為O(n4)的多項式算法。
Zhao和Tang[13]研究了帶有安裝時間和交貨期窗口與退化效應的單機排序問題,給出了計算復雜性都為O(nlogn)的多項式算法;Zhu等[14]研究了帶有交貨期窗口和維修的單機排序問題,其中維修存在資源且分為與位置相關和維修開始時間相關2種情況,給出了復雜性為O(n4)的多項式算法。在實際問題中,常常同時帶有安裝時間和交貨期窗口與維修活動,本文同時考慮了帶有上述情況的模型,并給出了在2種維修情況下的多項式最優算法。
1 問題描述
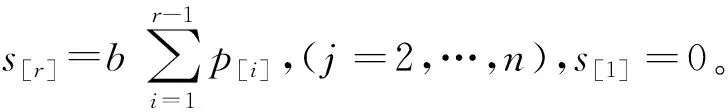
1=φ(0)≤φ(1)≤φ(2) ≤…≤φ(n-1)
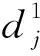
用三參數表示法將2個問題分別表示如下:


其中tdcrm表示與時間相關的維修活動,pdcrm表示與位置相關的維修活動,Spsd表示安裝時間。
2 對于帶有固定長度維修活動的最優排序的性質

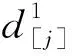
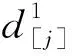
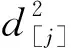
對于帶有交貨期窗口的單機排序問題,Mosheiov和Oron[10]證明了交貨期窗口的開始時間和完工時間不能發生在工件加工過程中,且維修活動如果發生,必排在一個延誤的工件之前。對于帶有安裝時間、維修活動和交貨期窗口的單機排序問題也有同樣結論。也就是:如果執行了維修活動,維修活動的開始時間一定被排在一個工件的完工時刻之后(或者在0時刻)。假設維修活動發生在第m個位置(l≤m),容易驗證本文有類似的結論如下:
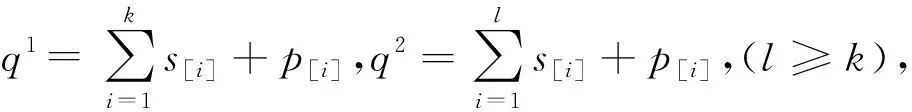
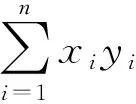
3 維修活動長度與時間相關的問題
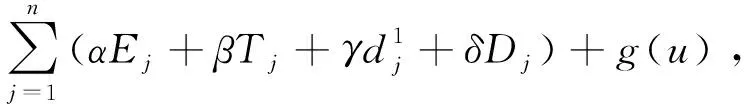
引理1 在最優排序中,若維修活動排在第m個位置,維修活動的位置只能屬于下列3種情況之一:
情況1 維修并未發生,即m=n+1;
情況2 維修活動在開始處發生,即m=0;
情況3 維修活動排在交貨期窗口之后,即l≤m 證明 假設排序為π=(J[1],…,J[n]),下面具體討論這個問題: 1) 維修并未發生。 (3) 交貨期窗口開始時間之和為 (4) 交貨期窗口的長度之和為 因為未發生維修活動,所以g(u)=g(0)=0。 則目標函數為 其中Wj為j位置的權,有 為了得到目標函數Z的最小值,將工件的加工時間p[j]與j位置的權Wj按照相反的順序排列。因此可以在O(nlogn)時間內得到最優排序。 2) 維修在機器開始加工時發生。 此時s=0,則維修活動的時間t(s,u)=t0+σs-τ(u)=t0-τ(u) (1)Ej=max(0,dj[1]-Cj),總提前量為 (3) 交貨期窗口開始時間之和為 (4) 交貨期窗口的長度之和為 則目標函數為 其中G(u)=γn(t0-τ(u))+g(u),Wj為j位置的權, 3) 維修在第m個位置發生,(l≤m (3) 交貨期窗口開始時間之和為 (4) 交貨期窗口的長度之和為 則目標函數為 其中G(u)=β(n-m)(t0-τ(u))+g(u),Wj為j位置的權。 家長要為孩子營造溫馨、寬松、自由的閱讀氛圍。閱讀時要安靜,沒有打擾,家長要帶領孩子開展形式新穎、內容豐富的閱讀活動。閱讀時,家長要給予孩子想象的空間,鼓勵孩子說出自己的想法,使孩子在愉悅的環境中快樂閱讀。 假設j工件排在第i個位置上,那么xij=1,否則xij=0。為了得到目標函數Z的最小值,可以將其轉化為指派問題: 其中: 對于資源分配的費用G(u)的最小值可以由u*=argmin{β(n-m)(t0-τ(u))+g(u)}得到,因為維修活動位置的不同,每一個位置需要求解一個相應的指派問題,因此可以在O(n4)時間內得到最優排序。 由以上討論,得到定理1。 問題4與問題3的性質類似,下面分別在3種情況下分析: 情況1 維修并未發生,即m=n+1; 情況2 維修活動在開始處發生,即m=0; 情況3 維修活動排在交貨期窗口之后,即l≤m 證明 假設排序為π=(J[1],…J[n]),維修活動的時間為t(m,u)=t0φ(m) -τ(u)。 維修并未發生與維修在開始時間發生的情況,與問題(1)和(2)一致,不再繼續討論,接下來討論維修并未發生與維修在開始時間發生的情況,與問題(1)和(2)一致,不再繼續討論,接下來討論維修在第m個位置發生的情況: 維修在第m個位置發生,(l≤m 3) 交貨期窗口開始時間之和為 4) 交貨期窗口的長度之和為 則目標函數為: 其中G(u)=β(n-m)(t0φ(m)-τ(u))+g(u),Wj為j位置的權, 假設j工件排在第i個位置上,那么xij=1,否則xij=0。為了得到目標函數Z的最小值,可以將其轉化為指派問題: 其中: 對于資源分配的費用G(u)的最小值可以由u*=argmin{β(n-m)(t0φ(m)-τ(u))+g(u)}得到。因為維修活動位置的不同,每一個位置需要解一個相應的指派問題,因此可以在O(n4)時間內得到最優排序。 由以上討論,可以得到下列定理: 本文研究了每個工件都有自己的交貨期窗口、安裝時間是加工時間的線性函數、維修帶有資源的單機排序問題。其中維修活動使工件的加工時間縮短,可以通過資源分配使維修活動長度減少。目標是找到交貨期窗口的大小和位置、維修的位置,使得提前懲罰、延誤懲罰、交貨期窗口的位置和長度、以及資源的總費用最小。在2種維修情況下,根據維修活動的位置不同分為3類,證明了問題是多項式可解的。另外,還可以在此基礎上繼續將模型推廣,比如帶有學習效應與退化效應的情況,也可以考慮工件的加工時間是帶有資源分配的。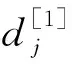

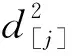

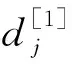


4 維修活動長度與位置相關的問題
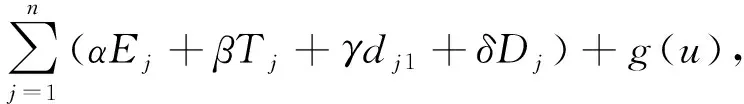


5 結 論

