人工神經網絡在導引頭去耦中的運用*

李相平,陸志毅

(海軍航空工程學院電子信息工程系,山東煙臺 264001)

0 引言

導引頭是決定導彈命中率的重要部分,主要是對目標的動態信息進行測量,通過機械裝置產生制導律從而使天線跟蹤目標。在導彈制導的過程中,噪聲、天線罩誤差以及干擾力矩等因素都會影響導彈的命中率。尤其是干擾力矩,可以說是回路中由于彈體質心不穩以及天線電軸與內部各零件摩擦帶來的最復雜的非線性影響因素,并且在導引頭跟蹤過程中對于干擾力矩十分敏感。所以為了能夠提升導彈的性能,對導引頭跟蹤回路中干擾力矩進行在線補償,隔離因為干擾力矩帶來的彈體擾動與導引頭耦合問題是當前需要解決的關鍵技術問題。文獻[1]提出一種前饋補償的算法對干擾力矩進行補償,但是只能用于處理簡單線性的回路系統,并且需要建立精確的模型,要求較高;文獻[2-3]從傳遞函數的角度上分析了線性化干擾力矩對導引頭視線角速率提取的影響,沒有給出具體的解決方案;文獻[4-5]論述了簡化后的彈簧力矩和阻尼力矩對導引頭性能的影響;文獻[6-7]研究了在存在雷達信號噪聲的情況下導引頭干擾力矩引起的隔離度問題,表明有噪聲時會增大隔離度對導彈脫靶量的影響。因此,由于干擾力矩存在帶來的隔離度問題不僅對導引頭輸出視線角速率的精度產生影響,還會惡化整個控制跟蹤回路的穩定性,降低導彈的命中精度。文中提出了一種基于神經網絡的前饋補償算法,通過對干擾力矩進行實時監督,進行自適應前饋控制,有效地解決保證輸出的信號誤差最小,較好地提升了導彈的性能。

1 干擾力矩模型的建立

1.1 質量不平衡引起的干擾力矩

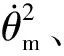
mr0cos(θl-θh-θm-θ0)am

(1)

式中:m是導引頭的質量;θh是天線電軸與彈體中心線的偏離角;θm是彈體角;θl是導彈攻角;r1是彈體重心和天線電軸之間的距離;am是導彈橫向加速度。

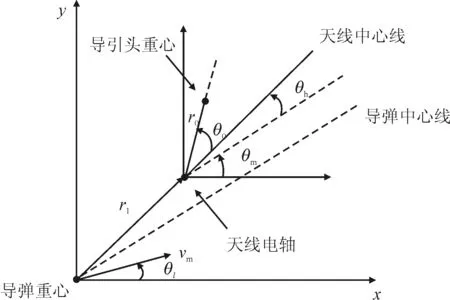
圖1 導彈的幾何構型圖

補償距離r0對導彈的性能影響很顯著,尤其是對導彈脫靶量。圖2表示導彈脫靶量的均方根與r0的變化曲線。可以看到,即使很小的r0也會造成很大的脫靶量。

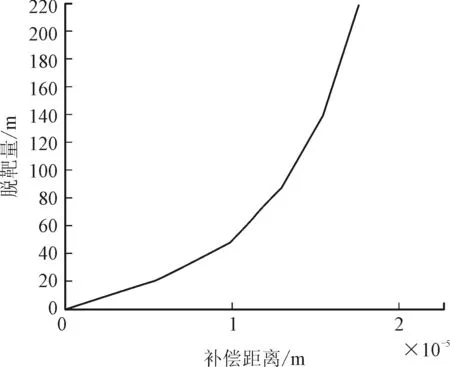
圖2 質量不平衡對導彈脫靶量的影響

1.2 天線電軸摩擦引起的干擾力矩

由于導引頭構造復雜,其內部零件眾多,因此帶來的摩擦是非線性的,這里主要討論天線電軸摩擦引起的干擾力矩,其表達式為:

(2)

其對應的變化曲線如圖3所示。

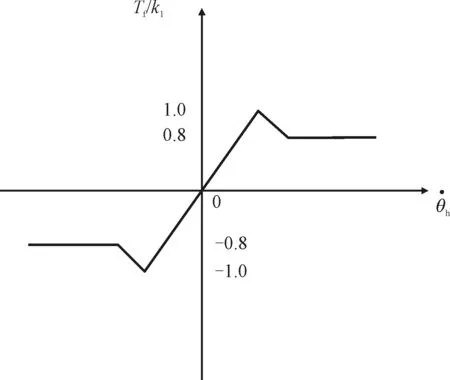
圖3 摩擦力矩表達式示意圖

為了表示摩擦引起的干擾力矩對導彈性能的影響,將導彈脫靶量隨摩擦系數k1變化的曲線圖引入,如圖4所示。

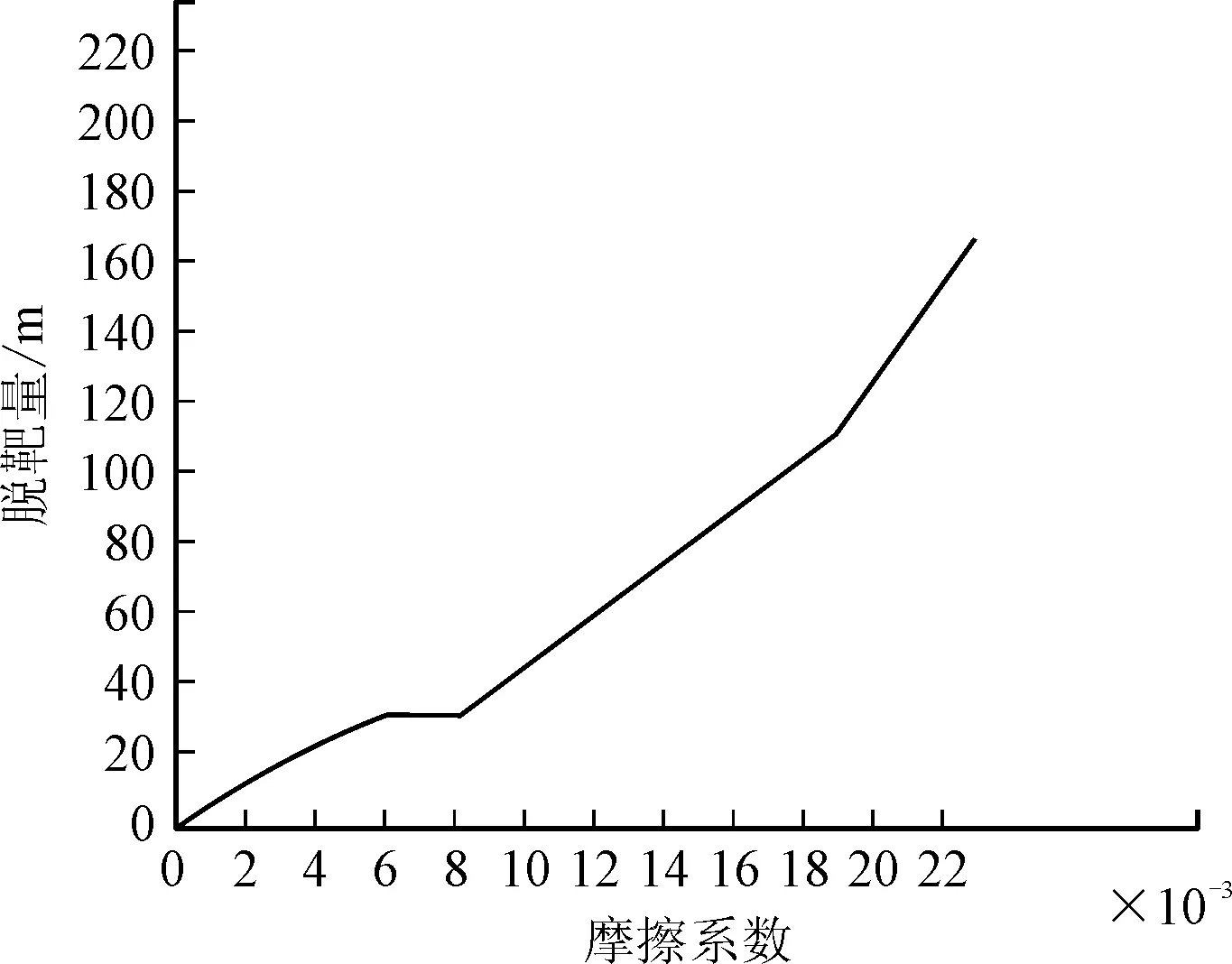
圖4 摩擦系數對脫靶量的影響曲線圖

那么對于整個導引頭跟蹤控制回路來說,其因為導彈質量不平衡和天線電軸摩擦帶來的系統干擾力矩為Td=Tm+Tf,為了隔離系統干擾力矩對導彈性能的影響,必須要對干擾力矩進行在線補償。

2 神經網絡補償的原理

為了解決導引頭干擾力矩引起的隔離度問題,可以采用多層感知器神經網絡進行力矩補償。多層感知器網絡有較強的分類能力,能夠處理非線性的問題,主要包括輸入層、隱含層和輸出層,其中隱含層可以是一層或多層,可以完成較復雜的任務。對于多層感知器中的每個神經元來說,激活函數通常取可微的函數,比如sigmoid函數:

(3)

式中:ui是第i個神經元的輸入信號;vi表示第i個神經元的輸出信號。

2.1 生物神經元的結構

人工神經網絡實際上是從生物神經網絡發展而來的,對于一個人而言,在大腦皮層大約有100億個神經元,60萬億個神經突觸以及它們的連接體[9]。人的大腦在學習的過程就是神經元之間連接強弱程度變化的過程,最終對信息的處理也是綜合神經元細胞的整體狀態來確定的。

具體的,每個神經元是由細胞體、樹突、軸突以及突觸組成。細胞體是神經元的主體部分,是給神經元提供能量的重要場所;樹突則是由細胞體向外界延伸的神經纖維,這些神經纖維有許多突起,可以通過它們來接收來自其他神經元的信息;軸突則是向外延伸最長的神經纖維分支,相當于輸入端口,主要是傳出神經沖動[10];突觸是神經元之間進行通信的接口。經過現代的生理學研究表明,大腦的活動并不是通過多個生物神經功能簡單疊加完成的,而是許多神經單元非線性的動態處理。所以,由此轉化而來的人工神經網絡可以較好地處理一些非線性問題,可以用于導引頭干擾力矩的補償和去耦。

2.2 神經網絡的學習算法

針對影響干擾力矩的因素,可以通過多感知器的神經網絡不斷進行學習和訓練,最終使得干擾力矩得到補償,保證輸出的信號誤差最小,其算法原理框圖如圖5所示。

圖5 導引頭神經網絡補償算法原理框圖

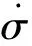
在該模型中誤差函數為:

(4)

對于神經網絡的輸入和輸出,可以用下式表示兩者之間的關系:

netj=Wjzj-1

zj=fj(netj),j=1,2,3,…,N

(5)

式中：fj(·),j=1,2,3,…,N是選取的激活函數,這里取sigmoid函數；zj-1和zj分別是神經元的輸入和輸出信號；Wj是每個神經元的連接權重。

對于感知器各層之間的權重,可以用BP算法進行學習,其詳細的學習過程如下:

1)隱含層第二層和輸出層之間權重U的學習為:

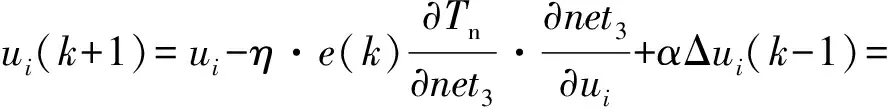
(6)

式中:

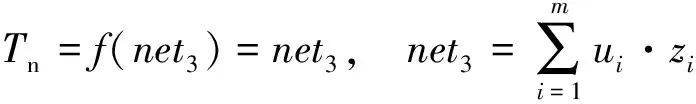
式中：關于net2i的定義在式(7)中有說明。

2)隱含層之間的權重V的學習為:

vij(k+1)=vij(k)-η·e(k)·ui(k)·f′(net2i)·

yj(k)+αΔvij(k-1)

(7)

式中:

yj=f(net1j),i=1,2,3,…,m;j=1,2,3,…,n

3)輸入層和隱含層第一層之間權重W的學習為:

f′(net1i)·aj+αΔωij(k-1)

(8)

式中:

i=1,2,3,…,n;j=1,2,3,…,7;l=1,2,3,…,m

3 仿真結果與性能分析

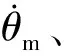
圖6 未補償系統的脫靶量和干擾力矩的曲線圖

通過設計的感知器神經網絡不斷進行學習和訓練,對補償后的導彈脫靶量和干擾力矩進行仿真實驗,其結果如圖7所示。

圖7 補償后系統的脫靶量和干擾力矩的曲線圖

通過仿真結果發現,未進行補償前導彈的脫靶量受干擾力矩的影響十分明顯,并且脫靶量的范圍很大,極大程度上降低了導彈的性能。通過文中設計的感知器神經網絡進行干擾力矩的前饋補償后,脫靶量有了很大程度的改善,表明應用多感知器神經網絡算法減小了系統干擾力矩的影響,一定程度上降低了因為干擾力矩帶來的耦合問題,提高了導彈的命中精度。

4 結論

由于多感知器神經網絡對非線性問題有很好的適應性,可以很好地模擬各個因素之間的變化情況,也不需要很多先驗知識和精確的模型,使問題處理起來更方便。同時在感知器輸入層、隱含層和輸出層之間權重的不斷訓練的過程中,參數得到改善,使得輸出的誤差減小。

通過設計多感知器的神經網絡模型處理導引頭干擾力矩問題,對導引頭產生干擾力矩的因素反復進行學習和訓練,產生與系統干擾力矩相近的力矩進行補償,達到了較好的效果,也表明神經網絡在導引頭去耦問題上的有效性和可行性。