一種亞聲速導彈氣動力計算方法*

王 剛,劉鈞圣,王 琨,趙軍民,楊云剛

(西安現代控制技術研究所,西安 710065)

0 引言

在戰術導彈概念設計階段,需要通過前期理論計算獲得較為合理或優化的氣動外形來滿足導彈性能要求(比如射程、過載、操穩特性等),為了達到這個要求,在方案設計初期就要建立具有一定計算精度和效率的氣動力計算模型,以便在總體設計迭代過程中,盡可能快速、準確的確定導彈總體參數。

目前工程上常采用兩種方法來評估導彈氣動特性。一種是工程預估方法[1-2],該方法主要是基于大量試驗數據擬合而得的經驗公式,它計算簡單,且幾乎沒有時間代價,但它無法反映特定構型真實的流場特性,故而計算精度較低;另一種是基于計算流體力學(CFD)的數值分析方法[3-4],該方法計算精度高,但也存在計算復雜且非常耗時的缺點。因此,上述二者方法對計算精度和計算效率的要求是相矛盾的。

針對以上問題,文中試圖建立一種具有中等計算精度的亞聲速導彈氣動力快速評估方法,為導彈概念設計階段的氣動力計算提供一種更為可行有效的途徑。

1 氣動力計算方法

文中將數值計算法和工程估算法有效結合,建立一種基于渦格法(vortex lattice method,VLM)的亞聲速導彈氣動力計算方法。該方法通過VLM來預測導彈升力、壓力中心、尾舵效率以及動導數。阻力則基于部件疊加的原理,將全彈阻力分解為彈翼阻力和彈身阻力。彈翼阻力由誘導阻力和型阻組成,采用渦格法來計算誘導阻力,型阻則通過基于XFOIL二維翼型數據的片條理論來預測;彈身阻力由摩擦阻力、壓差阻力和底部阻力構成,全部根據工程估算法來計算。

1.1 升力和壓力中心

采用Tornado VLM[5]計算軟件。亞聲速條件下,戰術導彈的升力絕大部分由翼面提供,故而在用Tornado VLM計算全彈升力時,僅考慮彈翼和尾舵對升力的貢獻。另外,由于VLM求解的是不可壓流,因此Tornado引入普朗特-格勞厄脫壓縮性修正因子來計算亞聲速狀態下的翼面升力。

LF=ρV2·αSF

(1)

(2)

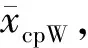
(3)

1.2 阻力

1)彈翼阻力

亞聲速條件下,彈翼阻力由誘導阻力和型阻構成。誘導阻力與升力相關,可直接通過Tornado VLM算出。型阻由粘性作用產生,通過基于XFOIL二維翼型數據的片條理論計算,方法如下:

①將彈翼沿展向劃分為28個片條,尾舵劃分為10個片條;

②根據每個片條對應的Ma數和Re數,利用XFOIL計算翼型的阻力極曲線:

(4)

③利用Tornado VLM計算彈翼各片條的升力系數Cl(y),并將其代入上式,得到彈翼剖面的阻力系數Cd(y);

④根據片條理論,沿展向數值積分可得到整個彈翼的型阻:

(5)

式中:Sstrip為片條所在彈翼劃分區間的面積;S為彈翼的參考面積。

2)彈身阻力

采用工程算法計算彈身阻力[7]。亞聲速彈身的阻力系數CDF主要由表面摩擦阻力系數CDFf、壓差阻力系數CDFp和底部阻力系數CDFb構成,即:

CDF=CDFf+CDFp+CDFb

(6)

①表面摩擦阻力系數

CDFf=RWF·CfF·SWetF/S

(7)

式中:RWF為翼身干擾因子,與彈身Re與Ma有關;CfF

為彈身的湍流平板表面摩擦系數;SwetF為彈身浸濕面積。

②壓差阻力系數

CDFp=RWF·CfF·[60/(l/dF)3+

0.0025(l/dF)]SwetF/S

(8)

式中:dF為彈身最大直徑。

③底部阻力系數

CDFb=0.029(db/dF)3/[(CDFf+CDFp)·

(S/SF)]1/2(SF/S)

(9)

式中:db為彈身底部直徑。

1.3 動導數

采用Tornado VLM計算俯仰阻尼力矩導數和滾轉阻尼力矩導數。Tornado計算動導數的原理為有限差分法。以俯仰方向為例,它假定導彈以兩種不同的角速度q1和q2等速上仰至相同攻角,根據小擾動理論對其力矩展開并略去高階量,則有:

(10)

(11)

(12)

2 算例

以某型戰術導彈為對象,開展算例研究。該導彈采用大展弦比正常式X-X氣動布局,外形如圖1所示,具體尺寸見表1,彈翼采用NACA0012翼型,尾舵采用NACA0010翼型,最大飛行Ma=0.6。

圖1 某型正常式X-X布局導彈氣動外形

導彈參數參數值彈身長度/m1.85彈身直徑/m0.15彈翼前緣與頭部的距離/m1.1彈翼展長/m0.9彈翼弦長/m0.095尾舵前緣與頭部的距離/m1.65尾舵展長/m0.3尾舵弦長/m0.08

為了對計算方法進行驗證,在沈陽FL60風洞對該導彈縮比模型(1∶2)進行了試驗,如圖2所示。

圖2 某導彈風洞試驗模型

3 結果與分析

3.1 計算效率

采用Tornado VLM對算例中的導彈建模,結果如圖3所示。圖3(a)顯示了導彈幾何外形,圖3(b)顯示了該導彈在Ma=0.3,α=2°,δe=4°條件下的壓力云圖。全彈共劃分為960個網格,采用Intel Xeon 2.80 GHz電腦運算時,單個狀態點僅耗時18.7 s,可以看出建立的氣動力方法具有較高的計算效率。

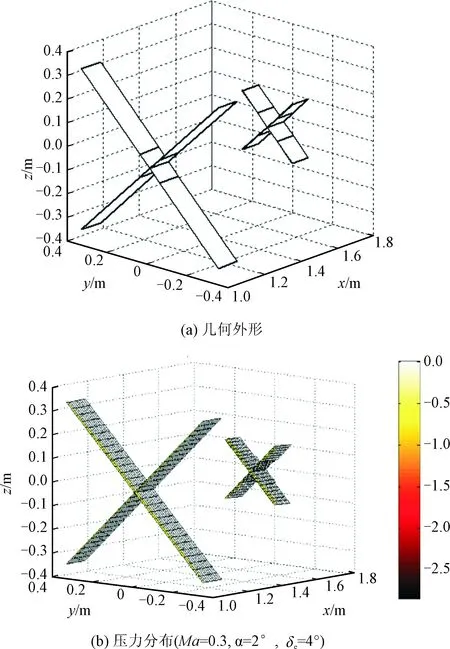
圖3 Tornado VLM對某型X-X布局導彈建模

3.2 與風洞試驗結果對比

在導彈續航狀態下(Ma=0.5),文中計算值與試驗值對比結果如圖4所示。由圖4(a)可知,當攻角小于8°時,升力系數具有良好的線性度,VLM計算方法也與試驗值吻合較好。隨著導彈攻角進一步增加(接近極限攻角),出現了比較明顯的流動分離,由于渦格法無法描述此現象,造成誤差為12%。

圖4 文中方法與風洞試驗結果對比(Ma=0.5)

圖4(b)顯示了阻力極曲線對比結果,可以看出文中預測的零升阻力比試驗值低了12.2%,誤差可能是由于未計入干擾阻力(如導彈與掛架之間的滑塊、彈翼與彈身之間的連接件等)所造成的。如果將此誤差當作常數計入氣動力計算方法中,見圖4(b)中的“文中方法修正”項,那么理論值與試驗值幾乎吻合,說明建立的阻力計算模型變化趨勢與風洞試驗是一致的。

壓力中心對比結果如圖4(c)所示,在考慮彈體頭部對壓心影響后,壓心預測值與試驗值之間的誤差可忽略不計。

圖5 Ma對文中方法計算精度的影響(α=2°)

圖4(d)顯示了Cnδe計算結果,從圖中可知,文中方法與風洞試驗對Cnδe的變化趨勢不一致,且在攻角超過6°之后,誤差增加較多。產生這一現象的原因是:如圖4(a)所示,隨著攻角增加,由于彈翼逐漸出現了流動分離,全彈升力不再保持線性變化,減小了升力線斜率。對于單獨尾舵來說,同樣存在類似現象,即降低了尾舵的效率。VLM在計算升力時并未考慮粘性作用的影響,最終導致計算值與實驗結果不一致。盡管如此,當攻角為8°時,VLM理論值與風洞試驗的誤差仍在12%以內。

圖5顯示了在巡航攻角(α=2°)條件下,不同Ma對文中方法計算精度的影響。從圖5(a)可以看出,低速條件下(Ma=0.3),升力系數誤差僅為6.5%,精度較高。隨著Ma增加,VLM與風洞試驗得到的升力系數均在增加,說明Prandtl-Glauert壓縮性修正因子可以反映升力系數隨Ma的變化趨勢,但誤差也逐漸增加,表明修正量偏大。對于文中研究的Ma≤0.6的亞聲速導彈來說,升力系數最大誤差為12%,在導彈概念設計時是可以接受的。由圖5(b)和圖5(c)可知,在低亞聲速條件下,Ma對阻力系數和壓心的影響較小。Ma對尾舵效率的影響與對升力系數的影響類似,由于壓縮性修正偏大導致誤差逐漸增加,使得最大誤差增加至7%,見圖5(d)。

3.3 與CFD計算結果對比

采用準定常方法[8],利用CFD通過模擬導彈定常拉升運動計算Cmq,模擬導彈勻速滾轉運動計算Clp。考慮到中等攻角(α≤10°)范圍內,攻角對Cmq和Clp影響較小[9],因此在導彈續航狀態下,探究了不同Ma對VLM和CFD關于動導數計算精度的影響。

圖6 文中方法與CFD關于動導數的計算結果對比(α=2°)

需要說明的是,Cmq是在導彈靜安定裕度SM=6.3%時計算的。從圖6可以看出,在低Ma下,Cmq和Clp的計算誤差較小,隨著Ma增加,誤差逐漸增加。當Ma=0.6時VLM與CFD計算兩個動導數的誤差為14%,精度能夠滿足導彈初步設計所需。

4 結論

1)建立了一種具有中等計算精度的亞聲速導彈氣動力快速評估方法。當馬赫數在0.3～0.6,攻角在0～8°范圍時,該方法與風洞試驗和CFD相比,各氣動參數最大計算誤差在15%以內,且單個狀態點的計算時間不超過20 s。結果表明:在導彈概念設計階段,該方法具有較好的精度和較高的效率,可用于導彈總體參數確定、氣動外形設計和飛行性能評估。

2)除正常式布局外,建立的計算方法還可用于鴨式布局和無尾式布局亞聲速導彈氣動特性的預測,為不同導彈方案選擇提供計算和分析手段。

3)當彈翼展弦比小于3時,由于彈翼存在較強的翼尖渦,產生了非線性渦升力,并伴隨攻角增加而愈加顯著[10],會導致渦格法計算誤差逐漸增大。因此,該氣動力計算方法僅適用于彈翼展弦比不小于3的導彈布局。