雜波與色噪聲條件下彈載雷達波形設計*

鄭家毅,翁木云,何 麗,李 偉

(1 空軍工程大學信息與導航學院,西安 710077;2 空軍電磁頻譜管理中心,北京 100800)

0 引言

隨著科技水平的進步,導彈目標向更小體積,更輕重量,更快速度發(fā)展[1],這就要求彈載雷達具有更高制導精度,而彈載雷達對目標參數(shù)估計性能是制約導彈制導精度的關鍵因素之一。基于認知理論,從優(yōu)化彈載雷達發(fā)射波形入手可有效提升彈載雷達對目標的參數(shù)估計能力,為提升導彈對目標檢測性能奠定基礎[2-3]。

圍繞雷達波形優(yōu)化設計,Bell[4]首次提出了基于互信息量(MI)準則的雷達波形設計方法;文獻[5-6]綜述了認知雷達關鍵技術(shù)及目標檢測的最優(yōu)波形設計方法;文獻[7]討論了MIMO雷達在MI和MMSE兩種準則下的波形設計,并指出在相同發(fā)射功率約束下,以這兩種準則優(yōu)化波形能得到相同的效果;針對雜波、噪聲條件下雷達波形設計問題,文獻[8]利用信噪比(SNR)和互信息準則(MI)研究了信號相關干擾條件下針對確定和隨機擴展目標的波形優(yōu)化問題;文獻[9]研究了色噪聲條件下基于MI和MMSE準則的波形優(yōu)化,并指出波形優(yōu)化結(jié)果與目標特征向量和色噪聲特征向量有關;文獻[10]研究了基于MI準則的MIMO雷達波形設計方法,并給出了目標、雜波特征向量與噪聲特征向量間的匹配順序。雖然文獻[8-10]等為雜波、噪聲條件下雷達波形優(yōu)化提供了很多有價值的方法,且優(yōu)化效果良好,但由于前述研究僅限于目標信息已知的波形優(yōu)化和優(yōu)化效果分析,且大多適用于MIMO雷達,前述研究難以應用于采用單天線的彈載雷達上。

針對上述問題,文中提出了雜波與色雜聲條件下基于線性最小均方誤差準則(LMSE)的彈載雷達波形設計方法。該方法通過理論分析和推導,在彈載雷達信號發(fā)射功率限制下,利用注水定理分配信號頻域能量,求解出優(yōu)化波形頻域能量分布具體表達式,從而提高彈載雷達對目標參數(shù)估計及檢測性能。

1 彈載雷達制導信號模型

彈載雷達回波模型如圖1所示。雷達發(fā)射信號s(t)能量有限,觀測時間為[0,T],帶寬為W,其傅里葉變換為S(f);h(t)為某持續(xù)時間有限的隨機擴展目標,傅里葉變換為H(f),與s(t)卷積得到目標散射回波z(t),其傅里葉變換為Z(f);n(t)為高斯色噪聲,均值為0,傅里葉變換為N(f),功率譜密度為Snn(f);c(t)為雜波沖擊響應,采用零均值高斯隨機過程描述,傅里葉變換為C(f),功率譜密度為Scc(f),與信號s(t)卷積得到雜波d(t),其傅里葉變換為D(f)。h(t)、c(t)、n(t)相互間統(tǒng)計獨立;y(t)為彈載雷達接收數(shù)據(jù),對應的傅里葉變換為Y(f)。

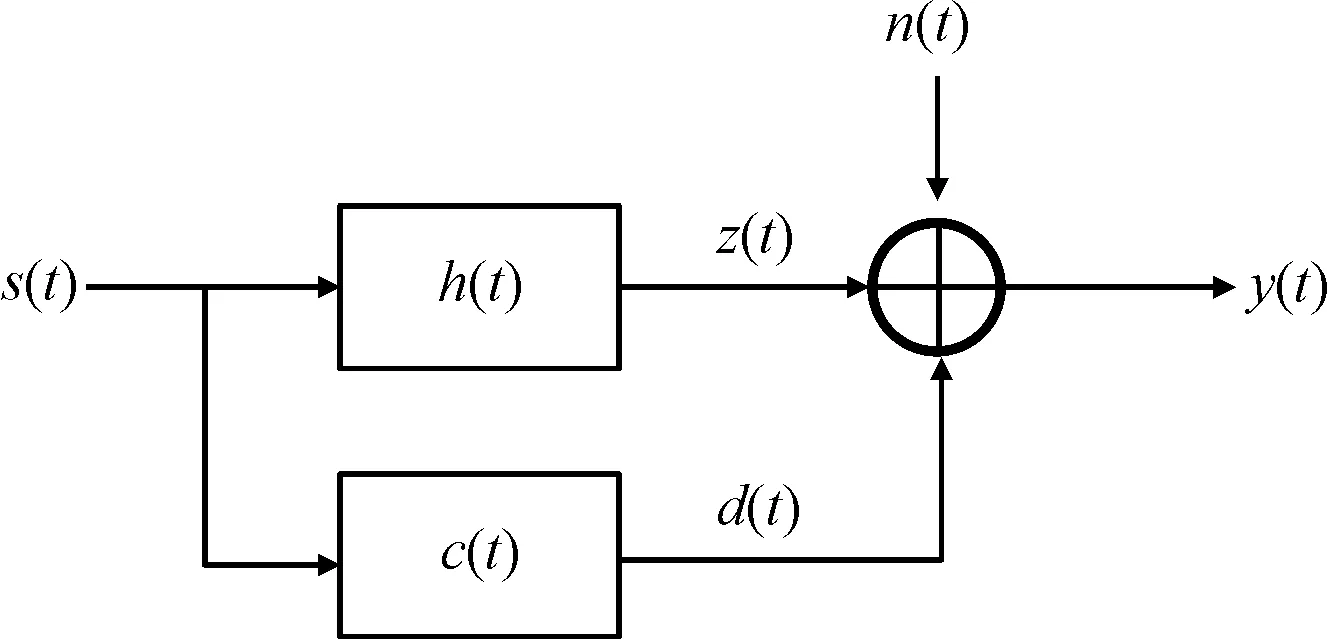
圖1 雷達回波模型

時域信號模型為:

y(t)=s(t)*h(t)+s(t)*c(t)+n(t)

(1)

頻域信號模型為:

Y=SH+SC+N

(2)

h(t)表征某隨機目標,持續(xù)時間為Th,其脈沖響應均值為0,平均能量為:

(3)

(4)

E[|z(t)|2]=E[|s(t)*h(t)|2]

(5)

值得注意的是,E[|h(t)|2]可被看作是一個平穩(wěn)隨機過程與一個矩形窗相乘得到,而E[|z(t)|2]是由一個時間有限的隨機脈沖響應與一個時間有限的波形的卷積得到的,因此,E[|z(t)|2]在[0,T+Th]內(nèi)是非平穩(wěn)的,不能用平均功率去描述,因此利用能量譜方差來描述E[|z(t)|2]:

(6)

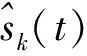
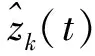
(7)

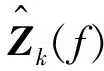
(8)

同理,雜波采樣點方差為:

(9)

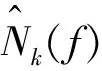
εN(Fk)=Snn(f)TΔf

(10)

采樣點方差為:

(11)

2 基于線性最小均方誤差準則(LMSE)的波形優(yōu)化算法

將認知理論應用于彈載雷達并根據(jù)某種特定準則設計最優(yōu)波形可有效提升彈載雷達檢測[11-12]、識別及跟蹤等性能。目前波形設計大多在目標信息已知的條件下開展研究,而彈載雷達剛開機時往往不具備充足的目標信息,因此提出一種針對目標最優(yōu)估計波形設計方法是必要的。以目標參數(shù)估計值與真實值間線性最小均方誤差[13]為準則(LMSE)來優(yōu)化波形能夠?qū)δ款l率響應進行貝葉斯估計,且該估計方法僅需目標與觀測值的前二階矩統(tǒng)計知識,在實際工作中容易滿足,所以得到廣泛應用。根據(jù)圖1回波模型,采樣點線性最小均方誤差估計子表達式為:

(12)

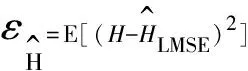
由于H與N為相互獨立且不依賴于發(fā)射信號的零均值高斯隨機變量,則有

(13)

上式對a求導并令其為0得:

E[2a-2H+bY]=0

(14)

故a=0。

對b求導并令其為零得:

E[2bY2-2HY]=0

(15)

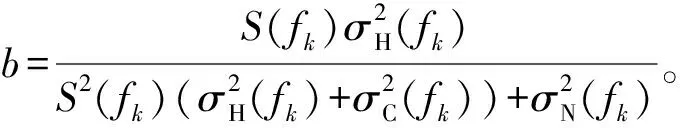
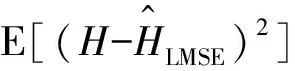
(16)

在2ΔfT個采樣點上的總均方誤差為:

(17)

當Δf→0時,上式可利用積分得到線性均方誤差:

(18)

因此波形優(yōu)化問題可轉(zhuǎn)化為以雷達發(fā)射機能量為限制,求目標估計誤差最小值問題:

(19)

利用拉格朗日乘子法:

(20)

式中λ為拉格朗日乘子,對式(20)關于|S(f)|2求偏導,令其結(jié)果為0,解得彈載雷達發(fā)射波形能量譜為:

(21)

(22)

令

(23)

(24)

(25)

(26)

考慮到發(fā)射信號能量譜非負,優(yōu)化后信號能量譜可表示為:

(27)

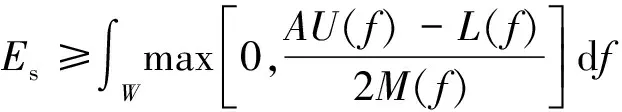
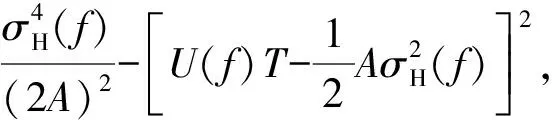
3 仿真分析

仿真試驗中,設彈載雷達發(fā)射信號載頻為fc=35 GHz,帶寬為W=10 MHz,彈載雷達觀測時間為1 ms,雷達接收機端采樣率為fs=20 MHz,根據(jù)多點散射模型產(chǎn)生目標沖擊響應,雜波、色噪聲均為零均值高斯隨機過程,彈載雷達初始發(fā)射信號為線性調(diào)頻信號,初始發(fā)射功率為P=10 W。

3.1 雜波色噪聲條件下波形優(yōu)化

圖2、圖3展示了目標、雜波及色噪聲功率譜密度,最終優(yōu)化結(jié)果如圖4所示。

圖2 目標及雜波功率譜密度

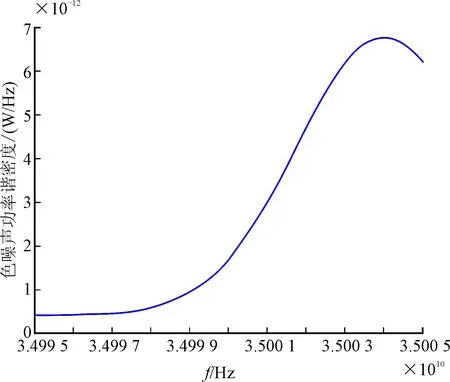
圖3 色噪聲功率譜

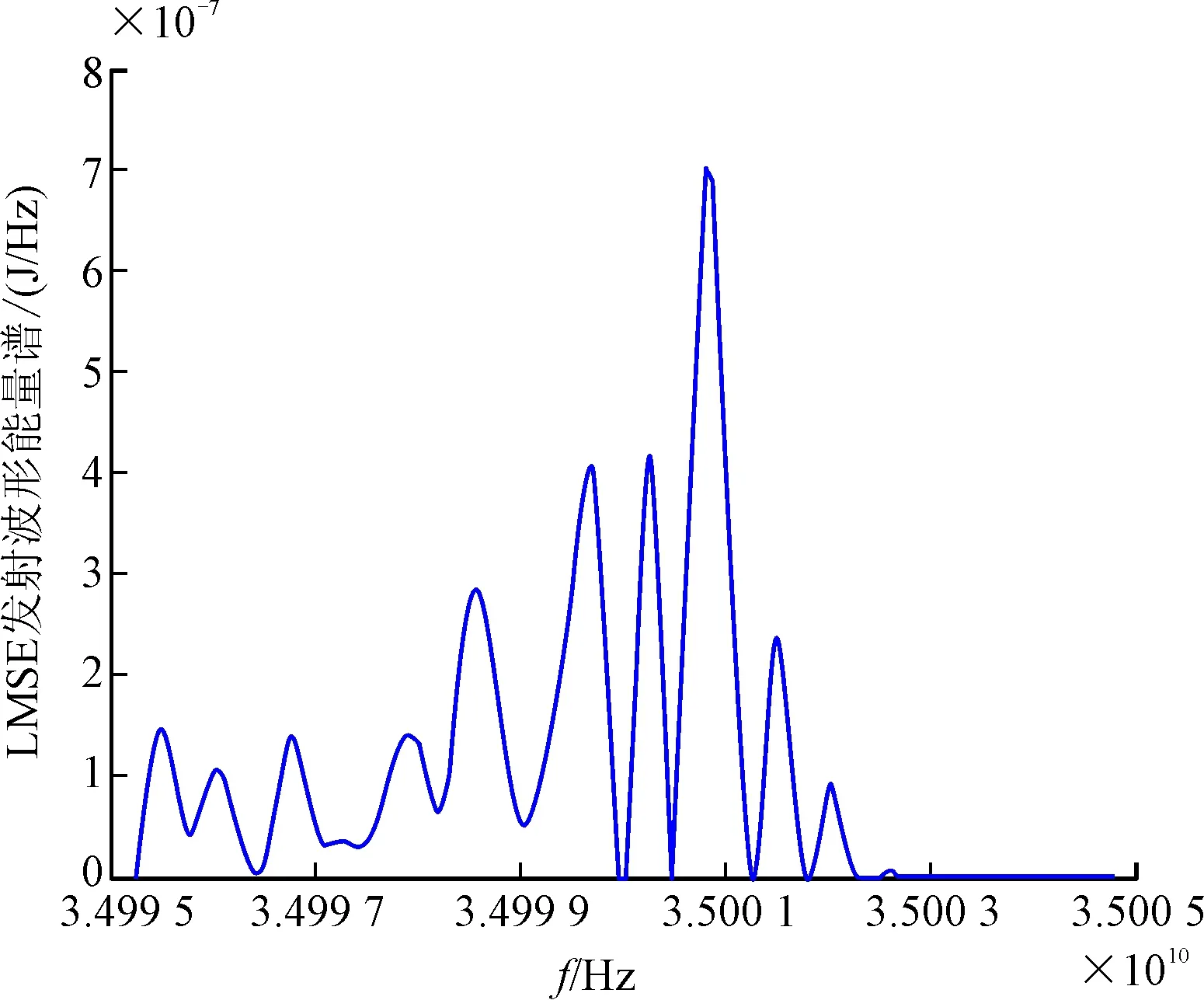
圖4 優(yōu)化信號能量譜

由圖4可以看出,優(yōu)化后的波形主要將能量分配在目標頻率響應相對較大且雜波、色噪聲相對較小的頻段內(nèi),而在雜波、色噪聲較大的頻段處,發(fā)射信號能量分配較少甚至不分配能量。由前文分析可知,在雜波,色噪聲較強處,目標頻率響應真值與估計值間誤差較大,發(fā)射信號在該處分配較少的能量會降低總體均方誤差,該仿真結(jié)果與理論分析一致。

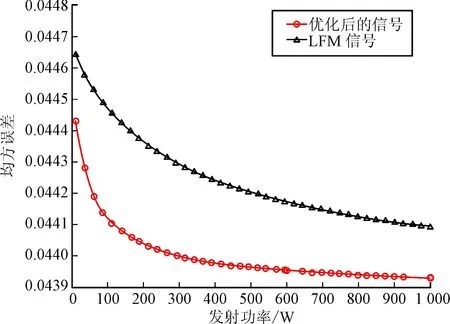
圖5 發(fā)射功率對均方誤差的影響

彈載雷達的參數(shù)估計性能往往受到信號發(fā)射功率限制。如圖5所示,隨著彈載雷達信號發(fā)射功率的增大,均方誤差逐漸減小,最后趨于穩(wěn)定。當發(fā)射功率較小時,優(yōu)化前后彈載雷達估計目標頻率響應的均方誤差相差較小,這是由于此時目標回波與色噪聲、雜波相比較小,目標頻率響應難以估計;隨著發(fā)射功率的提升,優(yōu)化前后均方誤差的差值逐漸增大,此時目標回波增強,且優(yōu)化后的發(fā)射信號能夠自適應的調(diào)整發(fā)射信號能量譜密度,減小總體均方誤差,而LFM信號沒有利用環(huán)境信息;當發(fā)射功率足夠大時,色噪聲相比目標回波較小,對估計誤差的影響可以忽略不計,優(yōu)化前后性能差異逐漸縮小,因此總估計誤差趨于一個定值,即

該結(jié)論與圖5的仿真結(jié)果一致。綜上所述,相比優(yōu)化前信號,以LMSE準則設計彈載雷達波形能夠更精確的估計目標頻率響應。

3.2 波形優(yōu)化前后檢測性能分析

以LMSE為準則優(yōu)化的發(fā)射信號相比LFM信號不僅能提升彈載雷達對目標頻率響應的估計精度,同時可有效改善雜波及色噪聲條件下對目標的檢測性能。根據(jù)前文建立的彈載雷達信號模型,構(gòu)建一種合理的檢測準則以檢測目標是否出現(xiàn),則目標檢測問題可描述為在兩種假設中進行選擇:H0(目標不存在)或H1(目標存在)。該假設可進一步表示為:

(28)

由于在真實場景中不能準確獲取H信息,因此式(28)中H值可采用式(12)的估計值代替真實值。針對上述二元假設檢驗問題可根據(jù)Neyman-Pearson準則構(gòu)建最優(yōu)檢測器[12],而能夠表征該檢測器性能的一個關鍵指標為信雜噪比(SCNR)。波形優(yōu)化前后彈載雷達接收機端信雜噪比如圖6所示。

圖6中所示,以LMSE準則優(yōu)化后的信號相比優(yōu)化前LFM信號能夠顯著提高彈載雷達接收機信雜噪比。值得注意的是,當信號發(fā)射功率達到一定值時,噪聲對信雜噪比的影響可忽略不計,雷達接收機端信噪比趨于穩(wěn)定,即

LFM信號相比優(yōu)化信號信雜噪比提升速率更低,但最終也會達到相同的定值。在此基礎上,優(yōu)化前后彈載雷達對目標檢測性能如圖7所示。

圖6 優(yōu)化波形與LFN波形SCNR

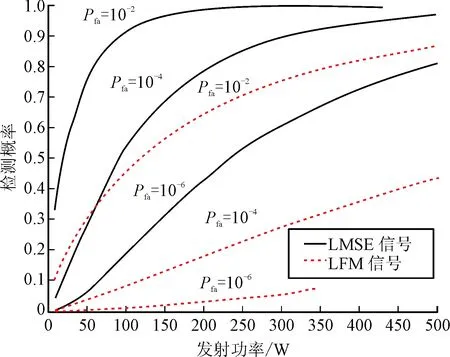
圖7 優(yōu)化波形與LFM波形檢測性能

圖7中展示了虛警概率分別為Pfa=10-2,Pfa=10-4及Pfa=10-6條件下,彈載雷達對目標檢測概率隨發(fā)射功率變化趨勢。從圖中可以看出,當虛警概率為Pfa=10-2,發(fā)射功率為250 W時,彈載雷達發(fā)射優(yōu)化信號可最先達到最高檢測概率,而此時發(fā)射LFM信號的檢測概率僅為0.7,若要得到最高檢測概率,發(fā)射功率需達到500 W甚至更高;當發(fā)射功率相同時,隨著虛警概率的增大,彈載雷達發(fā)射優(yōu)化信號與LFM信號間檢測概率差異如表1所示:

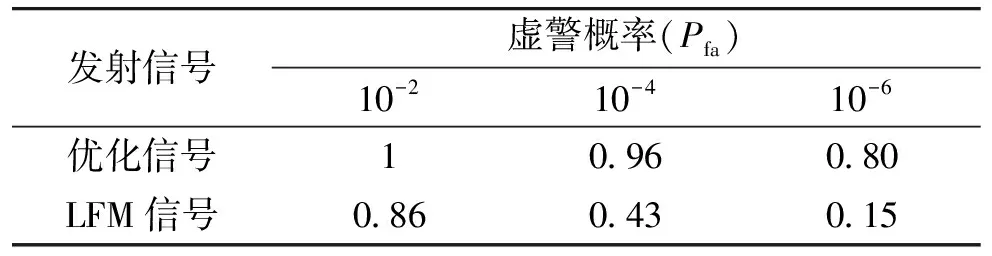
表1 發(fā)射功率為500 W時檢測概率對比

從表1中可以看出,當發(fā)射功率相同時,虛警概率由Pfa=10-2變化到Pfa=10-6時,發(fā)射信號優(yōu)化后檢測概率隨虛警概率變化下降0.2,而發(fā)射LFM信號后檢測概率變化0.71;當虛警概率相同時,發(fā)射優(yōu)化信號的檢測概率均高于LFM信號。綜上所述,相比LFM信號,優(yōu)化信號能顯著提高彈載雷達對目標的檢測概率且檢測性能更穩(wěn)定。

4 結(jié)論

導彈飛行速度快,信息獲取實時性要求高,如何能夠快速準確的獲取目標信息直接制約著導彈制導精度。針對以上問題,文中提出了一種在雜波與色噪聲條件下面向隨機擴展目標的彈載雷達波形優(yōu)化方法。該方法建立信號模型,基于認知理論以線性最小均方誤差為準則,采用注水法在頻域內(nèi)優(yōu)化彈載雷達發(fā)射信號能量分配,提升彈載雷達對目標頻率響應的估計能力。結(jié)果表明,算法可針對目標頻率響應、雜波及色噪聲的相對強度合理分配發(fā)射信號的頻域能量,提高目標估計精度,進一步提升彈載雷達對目標檢測性能。