新理念新設(shè)計(jì)
——點(diǎn)和線教學(xué)案例

（河北省隆化縣第二中學(xué) 河北隆化 068150）

教材：義務(wù)教育教科書 數(shù)學(xué) 七年級(jí) 上冊(cè)（河北教育出版社）第66——68頁(yè)

教材分析：

本節(jié)課的內(nèi)容是點(diǎn)、線段、射線、直線的認(rèn)識(shí)及表示，點(diǎn)和直線的位置關(guān)系，兩點(diǎn)確定一條直線的基本事實(shí)。本節(jié)內(nèi)容是圖形與幾何的起始課，是對(duì)幾何圖形進(jìn)行系統(tǒng)、深入學(xué)習(xí)的開(kāi)始。點(diǎn)和線是兩個(gè)最基本的幾何圖形，是構(gòu)成其他幾何圖形的基本要素，也是幾何圖形后續(xù)內(nèi)容學(xué)習(xí)的基礎(chǔ)。從現(xiàn)實(shí)生活中抽象出幾何圖形是學(xué)習(xí)幾何的重要方法，也是重要的學(xué)習(xí)方法，在本節(jié)中應(yīng)開(kāi)始逐步滲透。幾何語(yǔ)言是學(xué)習(xí)幾何的重要工具，本節(jié)課要使學(xué)生逐步聽(tīng)懂畫圖的要求、畫出正確圖形、表達(dá)出圖形及畫圖的過(guò)程。探究點(diǎn)和直線的位置關(guān)系和兩點(diǎn)確定一條直線是通過(guò)合情推理獲得的，合情推理是探索思路、發(fā)現(xiàn)結(jié)論的重要思維方式，也是學(xué)習(xí)和生活常用的思維方式，在本節(jié)應(yīng)予以重視。

本節(jié)課看似簡(jiǎn)單，但內(nèi)涵極為豐富，其中蘊(yùn)含著抽象、推理等思想方法和幾何語(yǔ)言的運(yùn)用與畫圖等基本技能，如果只關(guān)注知識(shí)點(diǎn)，這些事關(guān)學(xué)生數(shù)學(xué)素養(yǎng)和創(chuàng)新等課程目標(biāo)就難以落實(shí)，因此，全面落實(shí)課程標(biāo)準(zhǔn)，讓“人人都能獲得良好的數(shù)學(xué)教育”應(yīng)從每一節(jié)課做起。

教學(xué)目標(biāo)：

1.通過(guò)實(shí)際情境感知點(diǎn)和線段，認(rèn)識(shí)點(diǎn)、線段、射線和直線等幾何圖形。初步滲透用抽象的方法認(rèn)識(shí)事物。

2.通過(guò)觀察和畫圖了解線段、射線、直線的關(guān)系及它們的表示方法。

3.通過(guò)觀察和操作理解點(diǎn)和直線的位置關(guān)系，理解并掌握“經(jīng)過(guò)兩點(diǎn)有一條直線，并且只有一條直線”的基本事實(shí)。

教學(xué)重點(diǎn)：線段、射線、直線的認(rèn)識(shí)。

教學(xué)難點(diǎn)：幾何語(yǔ)言的運(yùn)用和“經(jīng)過(guò)兩點(diǎn)有一條直線，并且只有一條直線”基本事實(shí)的理解。

教學(xué)流程：

一、情景導(dǎo)入

夜晚在外面漫步，滿天的繁星閃爍，偶爾有流星劃過(guò)留下一道明亮的光線，滿天的繁星和流星劃過(guò)的光線，都給我們以怎樣的形象呢？這節(jié)課我們就來(lái)學(xué)習(xí)最基本的幾何圖形——點(diǎn)和線。

[設(shè)計(jì)意圖]聯(lián)系身邊的實(shí)際，導(dǎo)入新課，親切自然，體現(xiàn)了數(shù)學(xué)與現(xiàn)實(shí)的關(guān)系.

二、認(rèn)識(shí)點(diǎn)和線段

活動(dòng)1

（1） 在圖1中找出表示北京、天津、西安石家莊和鄭州等城市位置的點(diǎn)，并用筆加重描出圖中河北省與山西省的公共邊界線。

[設(shè)計(jì)意圖]讓學(xué)生在做的過(guò)程中抽象出點(diǎn)和線段，親身經(jīng)歷并在頭腦中建立起從身邊的實(shí)際問(wèn)題——幾何圖形的認(rèn)識(shí)過(guò)程。初步體會(huì)抽象的基本思想。

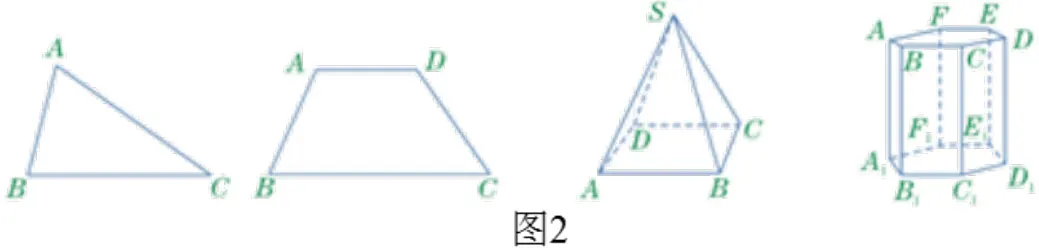
（2）在圖2中請(qǐng)指出平面圖形的頂點(diǎn)和邊，立體圖形的頂點(diǎn)和棱。

師：點(diǎn)的形象隨處可見(jiàn)，地圖中城市的位置，旅游圖中景點(diǎn)的位置，天空中的星星等都給我們以點(diǎn)的形象。從描兩省邊界線的過(guò)程可知，點(diǎn)動(dòng)。

[設(shè)計(jì)意圖]指出圖形中頂點(diǎn)和邊，一是認(rèn)識(shí)點(diǎn)和線段，二是在“指出”的過(guò)程中嘗試著對(duì)點(diǎn)和線段的表達(dá)（表示）。

象拉直的一段線、跳高的橫桿、直尺的邊緣等都給我們以線段的形象。平面圖形的邊、立體圖形的棱等都是線段。請(qǐng)你再舉出幾個(gè)給我們以線段形象的實(shí)例。

生：桌子的邊緣、黑板的邊緣、門的棱等。

師：如何表示點(diǎn)？如何表示線段呢？

由已有經(jīng)驗(yàn)和圖2的啟示，學(xué)生可自主完成，教師加以引導(dǎo)。

師：位于線段AB兩端的點(diǎn)A，B，叫做線段的端點(diǎn)。

對(duì)于線段AB，有的學(xué)生表示為“線段AB”，有的學(xué)生表示為“線段BA”，引導(dǎo)學(xué)生進(jìn)行評(píng)價(jià)，作出判斷，同時(shí)也使學(xué)生體會(huì)到了線段的兩個(gè)端點(diǎn)“地位相同”，表示沒(méi)有先后順序。

師：線段還可怎樣表示？學(xué)習(xí)用小寫字母表示線

[設(shè)計(jì)意圖]在學(xué)生主動(dòng)尋求表示的過(guò)程中，體會(huì)表示的合理性，進(jìn)一步理解端點(diǎn)。

三、認(rèn)識(shí)射線與直線

活動(dòng)2

按要求畫出圖形：

（1）畫線段AB；把線段AB向一方延伸。

（2）畫線段AB；把線段AB向兩方延伸。

[設(shè)計(jì)意圖]讓學(xué)生在動(dòng)手畫（做）的過(guò)程中加深了對(duì)射線、直線意義的理解，同時(shí)，一邊“聽(tīng)”，一邊畫，進(jìn)行了幾何語(yǔ)言的學(xué)習(xí)與訓(xùn)練。

師：這樣，我們就得到了兩個(gè)圖形，象（1）中的圖形，將線段AB沿AB方向（或BA方向）無(wú)限延伸所形成的圖形，叫做射線，點(diǎn)A（或點(diǎn)B）叫做射線的端點(diǎn)。

象（2）中的圖形，所得的幾何圖形叫做直線。將線段AB沿這條線段向兩方無(wú)限延伸所形成的圖形，叫做直線。

請(qǐng)你嘗試著表示（1）中的射線和（2）中的直線。

[設(shè)計(jì)意圖]在嘗試表示的過(guò)程中，進(jìn)一步理解線段、射線、直線表示的合理性，以及它們之間的聯(lián)系與區(qū)別。

學(xué)生在表示的過(guò)程中，可能會(huì)出現(xiàn)一些不同的想法：

如射線AB，射線BA；直線AB，直線BA；直線a，直線l等。

教師引導(dǎo)學(xué)生分析評(píng)價(jià)，得到射線、直線的表示。從中體會(huì)線段、射線、直線表示的合理性，以及圖形表示的“規(guī)則”。

[設(shè)計(jì)意圖]體會(huì)圖形表示的“規(guī)則”，有利于后續(xù)學(xué)習(xí)圖形的表示，如以O(shè)為頂點(diǎn)的角表示為∠AOB或∠BOA，直線a與b平行，表示為a∥b或b∥a，以A，B，C為頂點(diǎn)有三角形表示為△ABC，或△BCA等。

四、探究點(diǎn)與直線的位置關(guān)系

活動(dòng)3

（1）如圖2，小鳥(niǎo)A落在了電線l上嗎？小鳥(niǎo)B落在了電線l上嗎？

[設(shè)計(jì)意圖]通過(guò)觀察圖片、動(dòng)手畫圖等，把實(shí)際問(wèn)題抽象成了幾何圖形，并獲得點(diǎn)與直線位置關(guān)系的認(rèn)識(shí)。

（2）按要求畫圖：

綜上所述，經(jīng)肛門局部切除術(shù)治療距肛緣距離≤8 cm的T1N0期直腸癌患者可獲得與直腸癌根治術(shù)相似的預(yù)后，且有助于減少術(shù)后并發(fā)癥，患者年齡、腫瘤分化程度及切緣性質(zhì)是影響局部切除術(shù)患者預(yù)后的獨(dú)立因素，可作為直腸癌局部切除術(shù)患者手術(shù)適應(yīng)癥的選擇依據(jù)。

①畫直線l，點(diǎn)A在直線l上；

②畫直線l，點(diǎn)B在直線l外；

③有沒(méi)有既在直線l上，也不在直線l外的點(diǎn)？

[設(shè)計(jì)意圖]獲得點(diǎn)和直線的位置關(guān)系是合情推理，結(jié)果的正確性需要進(jìn)一步驗(yàn)證（或證明）。（3）平面內(nèi)的一點(diǎn)P與直線l有怎樣的位置關(guān)系？請(qǐng)你畫圖并進(jìn)行說(shuō)明。

師：如果點(diǎn)P在直線AB上，也在直線CD上，即點(diǎn)P是直線AB和CD的公共點(diǎn)，我們稱直線AB與CD相交于點(diǎn)P。

[設(shè)計(jì)意圖]使學(xué)生養(yǎng)成畫圖、借助于圖形解決問(wèn)題的習(xí)慣。

五、探究直線的基本事實(shí)

活動(dòng)4

（1）把一根木條釘在墻上。

②用兩根釘子釘，木條能轉(zhuǎn)動(dòng)嗎？

這種現(xiàn)象說(shuō)明了什么？

[設(shè)計(jì)意圖]讓學(xué)生親身經(jīng)歷“實(shí)驗(yàn)—畫圖—得到數(shù)學(xué)事實(shí)”的過(guò)程，使學(xué)生理解“經(jīng)過(guò)兩點(diǎn)有一條直線，并且只有一條直線”的基本事實(shí)。

（2）用直尺畫直線

①經(jīng)過(guò)一點(diǎn)畫直線，能畫幾條？

②經(jīng)過(guò)兩點(diǎn)畫直線，能畫幾條？

[設(shè)計(jì)意圖]進(jìn)一步體會(huì)從生活現(xiàn)象抽象為幾何圖形，并研究幾何圖形的方法。

由此，能得到怎樣的結(jié)論？

師：這樣我們就得到：

基本事實(shí) 經(jīng)過(guò)兩點(diǎn)有一條直線，并且只有一條直線。

[設(shè)計(jì)意圖]由實(shí)際操作或思考固定木條的過(guò)程、畫圖驗(yàn)證等獲得基本數(shù)學(xué)事實(shí)，經(jīng)歷抽象和獲得數(shù)學(xué)事實(shí)（結(jié)論）的過(guò)程，初步了解了合情推理、演繹推理的過(guò)程。

六、鞏固練習(xí)

1.判斷下面的語(yǔ)句是否正確：

（1）畫一條直線等于3cm；

（2）射線AB和射線BA是同條射線；

（3）線段AB和線段BA是同一條線段；

（4）射線是直線的一半；

（5）延長(zhǎng)直線AB至C，使AB=BC；

（6）如圖，射線OA和射線OB是同一條射線；射線OB與射線AB是同一條射線。

[設(shè)計(jì)意圖]1題的目的是理解線段、直線和射線，初步培養(yǎng)學(xué)生對(duì)幾何語(yǔ)言“聽(tīng)”的能力和“畫”的基本技能。

2.下列各圖中，哪個(gè)圖中的線段、直線或射線能夠相交？

[設(shè)計(jì)意圖]2題的目的加深對(duì)線段、直線、射線的理解（是否能夠延伸）。

3.按要求畫圖

（1）畫線段AB，延長(zhǎng)AB到C，使BC=1cm；

（2）畫點(diǎn)A，經(jīng)過(guò)點(diǎn)A作直線l，點(diǎn)Q在直線l外。2.射擊運(yùn)動(dòng)員怎樣瞄準(zhǔn)？

[設(shè)計(jì)意圖]3題是培養(yǎng)學(xué)生能夠讀懂幾何語(yǔ)言，并且全畫圖形。

七、解決問(wèn)題

1.如何把一行樹(shù)栽直？

2.射擊運(yùn)動(dòng)員怎樣瞄準(zhǔn)？

[設(shè)計(jì)意圖]對(duì)“經(jīng)過(guò)兩點(diǎn)有一條直線，并且只有一條直線”的鞏固應(yīng)用，同時(shí)也體現(xiàn)了數(shù)學(xué)知識(shí)與實(shí)際問(wèn)題的聯(lián)系。

八、拓展延伸

（1）經(jīng)過(guò)任意三點(diǎn)可畫多少條直線？經(jīng)過(guò)四點(diǎn)可以畫多少條直線？五點(diǎn)呢？

（2）在一次比賽中，明星排球隊(duì)擊敗了對(duì)手，隊(duì)員們用擊掌的方式歡呼勝利，每?jī)蓚€(gè) 人擊一次掌，12個(gè)隊(duì)員共擊掌 次.鞏固“經(jīng)過(guò)兩點(diǎn)有一條直線，并且只有一條直線”的數(shù)學(xué)事實(shí)，初步體會(huì)分類討論思想給解決問(wèn)題帶來(lái)的便利，發(fā)展數(shù)學(xué)思考。

[設(shè)計(jì)意圖]用數(shù)學(xué)知識(shí)解決實(shí)際問(wèn)題，使學(xué)生體會(huì)到數(shù)學(xué)的價(jià)值，同時(shí)感悟“問(wèn)題情境——建立數(shù)學(xué)模型——解釋、拓展與應(yīng)用”的模式。

九、小結(jié)

回顧本節(jié)內(nèi)容，你有哪些收獲？

本節(jié)課學(xué)習(xí)了點(diǎn)、線段、射線、直線及表示；點(diǎn)和直線只有點(diǎn)在直線上和點(diǎn)在直線外兩種位置關(guān)系；經(jīng)過(guò)兩點(diǎn)有一條直線，并且只有一條直線，這是一條基本事實(shí)，在以后的學(xué)習(xí)中可以直接運(yùn)用這個(gè)結(jié)論。

把城市的位置、天上的星星、拉直的一條線、跳高的橫竿等抽象成點(diǎn)和線段，這是重要的學(xué)習(xí)方法，也是常用的研究問(wèn)題、解決問(wèn)題的方法。點(diǎn)和直線的位置關(guān)系以及兩點(diǎn)確定一條直線的基本事實(shí)都是通過(guò)抽象身邊的事物或現(xiàn)象獲得的。

[設(shè)計(jì)意圖]幾何語(yǔ)言也象其他語(yǔ)言一樣，是學(xué)習(xí)幾何、進(jìn)行交流的重要工具，要求會(huì)聽(tīng)、會(huì)說(shuō)、會(huì)讀、會(huì)寫（畫）小結(jié)不是對(duì)學(xué)習(xí)內(nèi)容的簡(jiǎn)單回顧，而是在回顧基礎(chǔ)上的提升；不是對(duì)知識(shí)的簡(jiǎn)單總結(jié)，還是對(duì)形成這些知識(shí)的思想方法的提煉。

十、作業(yè)

習(xí)題A組，

選作：B組

1直線可把平面分成兩部分。

2條直線最多可把平面分成幾部分？

3條直線最多把平面分成幾部分？n條直線最多把平面分成幾部分？