例談創造性思維的自我培養

（湖南省長沙市周南梅溪湖中學 湖南長沙 410002）

創造性思維是個體不依照常規思考問題，尋求變異，建立新的理論，用新的思維、方可來解決問題的方式。[1]

在教學中，創新從來都是一個常談、常講、又常很困難的一件事情。老師在教學中難以把握，難以傳授。或者說老師自己本身就很難辦到，要求學生能夠做到就可想而知了。下面以從舉例法出發，針對創造性數學思維的自我培養方式進行探討和分析。

一、培養發散思維——從多方面多角度去思考問題

例如數形結合，立幾和向量結合，三角和函數結合，解幾和向量結合，數列和函數從而和圖形結合等等，都適合采用這種方式。

在傳統的數學教學活動中，一般是根據既定的內容、標準來傳授知識結構，從單向思維的角度來聯系內容學習公式、定理，這種思維模式是單一的，知識解決問題的基本方式。但是，如果一直按照這種模式來解決問題，必然會出現思維定勢，影響創造性思維能力的發展。[2]

尤其是在學期結束時期上復習課，老師可以把整個內容從整體上劃分為幾個大的部分，例如我在期末復習中，會將整個立體幾何和空間向量、棱柱和棱錐、球及歐拉公式從整體上聯系結合，將內容分成三個部分，即線線關系、線面關系、面面關系，學生在復習當中，普遍反映一下子要用到好多好多的知識，涉及高一、高三的內容；在對高三的高考內容的復習當中，我是結合導數和函數，導數和圖形，導數和不等式來復習的，達到很理想的效果，學生在無形中，可以將整個高中內容百分之80到百分之90的內容又過了一遍，好像不僅局限于高二的復習內容，突然覺得可以用很多方法來解決問題了。[3]

為此，在數學學習中，要掌握發散性思維的應用方式，掌握一題多解、一題多變等方法的應用，我們來看一個例題，舉例來說明發散思維該如何考慮。

根據題目的特點，可以從不等式、數列、函數、幾何、三角等內容來分析和思考，通過對比來找出最合適的解決方式，根據種種分析可以得出：

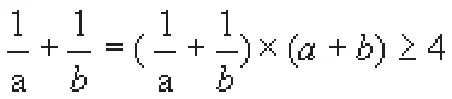
解決上述問題的最有效方式。除了該種方式之外，還可以改變題設、結論、條件來進行訓練。根據本題，可以采用如下的拓展方式：

通過一系列的訓練，可以從多個角度分析問題，加深自身對于知識的感受和理解，提高解題能力和思維能力。

二、善用逆向思維——“正難則反”的數學思維

如果采用從正面入手很難找到突破口，我們則會思考反面入手，即我們常說的逆向思維。常見方法以反證法最為突出。逆向思維最大的好處在于培養自己獨立的思考能力，鍛煉自己的頭腦。碰到較難找到方法的題目，請你常試著倒過來想一想。

正向思維就是以已知條件為出發點，按照常規的解題思路、先后順序來解決數學問題，所謂逆向思維，就是正向思維的相反，在解題時，應用逆向思維，能夠鍛煉獨立思考能力，突破學習中的難點和重點，將難題簡單化。

如，數 y=f（x）的圖象上的每一點的縱坐標不變，將橫坐標伸長至2倍，把圖象沿X軸向左邊平移個單位，再沿Y軸向下平移1個單位，得出的圖象和圖象相同，那么f（x）的表達式是？

在這一題目中，如果按照常規的思維來分析，解答過程十分繁瑣，為了簡化解題方式，可以嘗試采用逆向思維，讓解題過程變得簡單明了。

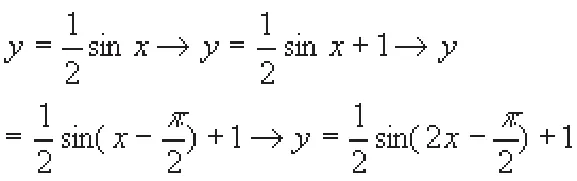
三、構建整體思維——整體思維是整體原理在數學中的反映

在解決數學難題的過程中，思維不一定集中在個別問題上，有的時候，將問題看做一個整體，往往可以取得意想不到的效果，對問題的整體結構、形式進行處理，即可簡單、順利的解決問題，即要學會站在一定的高度來看問題，先宏觀調控，在各個點來擊破。

例如，求sinl0°.sin30°.sin50°.sin70°的值.

在解決這一問題時，可以乘積看成整體，可得如下解法：設a=sinl0°.sin30°.sin50°.sin70°，b=cosl0°.cos30°.cos50°.cos70°兩式相乘然后運用倍角公式后可解得。

此外，還可以把a直接轉化為cos80°.cos60°.cos40°.cos20，通過這種轉化方式，讓解題過程變得更加簡單，老師在教學的時候可以以此來推廣，多讓學生總結。

再以某高考題為例：

四、注意直覺思維

在解決數學問題時，可以先對解題途徑、結果進行大概的猜測，得出大致的解題方向，這就是直覺思維，在解決數學問題時，不能忽視直覺的出現，這種直覺，往往是你在不經意中對這道題的一個宏觀把握，難怪有人說，在考試的時候，我突然靈光一現，會達到意想不到的結果。對于抽象的數學問題，都可以采用直覺思維來解決問題，將抽象思維轉化為形象思維，得出正確的答案。

思維是解決數學問題的基礎，也是重中之重，思維的核心，便是其創造性、獨立性，要解決數學問題，不僅要把握好定理、公式的應用，還要掌握思維方式的應用，以此來提高自身的素質，成為綜合能力過硬的人才。