讓知識可見

張存寶

知識導圖在一定程度上能夠將我們的筆記系統化和簡單化，使得相關的知識點及相互關系更加形象、明晰.有效利用知識導圖，能夠強化我們的記憶和理解，幫助我們構建知識網絡，就像找到一張“尋寶圖”，它啟發我們找到解題的線索、路徑.因此“知識導圖”有點像一張思路地圖，在高中數學復習中，一圖在手，對于知識的梳理、解題思路的探尋，均可發揮重要的作用.在這里我們以立體幾何中的平行關系為例進行說明.

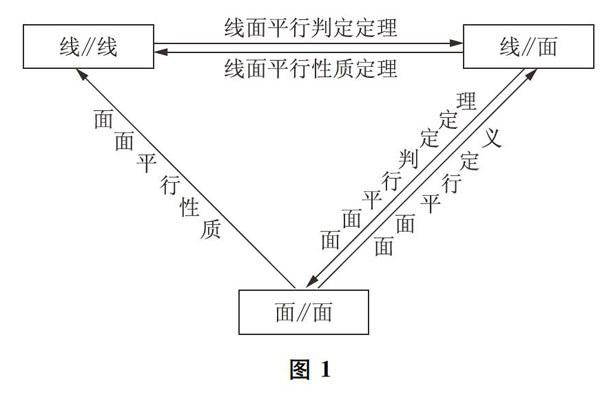
立體幾何的平行關系涉及多個定理，處理這部分知識、解有關立體幾何證明題，有時會覺得無從下手，更有甚者連基本的定理都沒有記住，更何況運用！在這里，我們根據線線、線面、面面平行之間的關系將各個定理進行串聯，形成知識網絡，進一步組成一張直觀、形象的知識導圖，這樣能夠一舉解決定理的記憶以及運用兩個問題.

以上知識導圖，可以簡單解讀如下：

跟隨箭頭所指的方向我們可以看到，要證線面平行，共有兩個箭頭指向線∥面，我們就有兩個思路.思路一：運用線面平行判定定理證線∥線；思路二：運用面面平行的定義證面∥面.反向來看，如果已知條件為線∥面，我們有兩個方向.方向一：運用線面平行性質定理可以得到線∥線；方向二：運用面面平行判定定理可以去證面∥面.總之，根據箭頭的方向可以得到你需要的條件或者結論.

比如，要證面∥面，我們發現在途中只有一個箭頭指向它，那么就說明，要證面∥面只能通過證線∥面來實現.通過知識導圖我們還可以看到，線∥線是不能證明面∥面的，但面∥面可以證明線∥線.我們通過一個具體例子來分析一下：

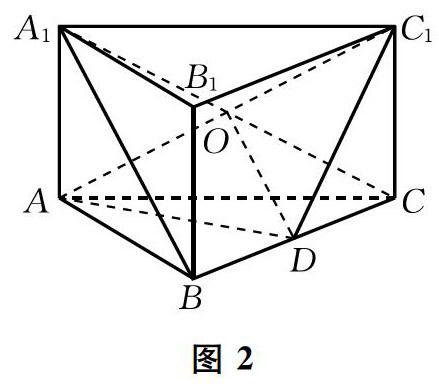
如圖2，在三棱柱ABC-A₁B₁C₁中，D是BC的中點.求證：A₁B∥平面ADC₁.

本題要證線∥面，由知識導圖可知有兩個思路：證明線∥線或者面∥面.而根據條件直三棱柱和D為中點，顯然證明線∥線更為簡單，因此，我們在平面ADC₁中尋找或者作一條輔助線與A₁B平行即可.證明如下：

連結A₁C，交AC₁于點O，連結OD.

由ABC-A₁B₁C₁是三棱柱得四邊形ACC₁A₁為平行四邊形，故O是A₁C的中點.

又D為BC中點，所以OD為△A₁BC中位線，所以A₁B∥OD.

因為OD?平面ADC₁，A₁B?平面ADC₁，所以A₁B∥平面ADC₁.

知識導圖在高中數學復習中的作用不可小覷，我們要在老師的引導和幫助下，根據自己的理解全面系統地梳理知識，畫成便于運用的知識導圖，促進解題能力的有效提高.