基于人工免疫粒子濾波算法的MIMO-SCFDE 系統信道估計方法

齊永磊，陳西宏，謝澤東

(空軍工程大學防空反導學院，陜西 西安 710051)

0 引言

多輸入多輸出(MIMO)是一種有效的抗多徑衰落的技術，研究表明，MIMO系統在不增加系統帶寬和天線總發射功率的情況下，可以明顯提高系統的抗衰落性能，提高系統的信道容量和頻帶利用率[1]。單載波頻域均衡(SC-FDE)的概念[2-3]由H.Sari等人在1994年提出，SC-FDE借鑒了正交頻分復用技術通過頻域均衡方法對抗頻率選擇性衰落的優點，同時保留了單載波信號峰均比低的優勢，而且相比單載波時域均衡，在大多徑時延時，頻域均衡的復雜度明顯降低[4-5]。將MIMO技術和SC-FDE技術相結合構成MIMO-SCFDE系統，可以在保證功率高效和抗頻率選擇性衰落的情況下進一步提高系統數據傳輸速率。

時變信道估計影響著MIMO-SCFDE系統通信性能，是其關鍵技術之一。遞歸最小二乘(RLS)算法、最小均方(LMS)算法和卡爾曼濾波(KF)算法都是經典的時變信道估計算法。相比另兩種，KF算法具有更好的性能，但其適用于線性高斯系統[6]，在文獻[7]中，Middleton指出，在通信系統中，環境噪聲多為非高斯分布，KF算法在此環境中性能不穩定；利用粒子濾波(PF)算法在非線性非高斯環境下估計的優勢[8-9]，文獻[10—11]分別成功地將經典PF算法用于MIMO系統和SC-FDE系統的時變信道估計，但經典PF算法會帶來權值退化的問題，從而影響信道估計的精度[12]；文獻[13]將人工免疫的思想引入粒子濾波中，可以有效緩解權值的退化，但其未將此算法應用在時變信道估計中進行研究。本文針對經典PF算法在MIMO-SCFDE系統時變信道估計中出現權值退化的問題，提出了一種基于人工免疫粒子濾波(AIPF)算法的MIMO-SCFDE系統時變信道估計方法。

1 MIMO-SCFDE系統

圖1展示了MIMO-SCFDE無線通信系統。此系統發射天線有nT個，接收天線有nR個，對經過映射后的數據進行串/并變換后形成nT個數據流；每個數據流在相應的發射天線上插入循環前綴(CP)后被發送出去，CP的長度必須大于信道最大時延擴展長度L，插入CP后可以使得信道沖激響應和發送信號的線性卷積等效為循環卷積，每個天線上發送數據流的數據幀結構如圖2所示。

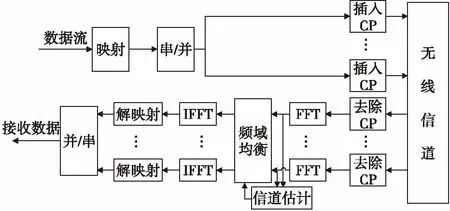
圖1 MIMO-SCFDE無線通信系統Fig.1 MIMO-SCFDE wireless communication system

圖2 每個發射天線數據流的幀結構
Fig.2 Frame structure for each transmitting

n時刻第t個發射天線上的數據可表示為：

(1)

式(1)中，wt(n)表示P×1的CP向量，dt(n)表示Q×1的數據向量；記K=Q+P。則xt(n)=[xt(n,1),…,xt(n,K)]T，t=1,…,nT。

發射信號進入無線信道，經無線信道傳播后被接收端接收，然后去除CP，n時刻去除CP后的接收信號可以表示為：

y(n)=h(n)x(n)+v(n)

(2)

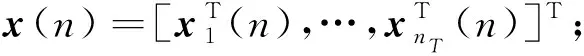
(3)

式(3)中，hr,t(n)表示n時刻第t個發射天線到第r個接收天線的信道沖激響應。

對接收數據進行快速傅里葉變換，FFT長度為Q，由文獻[14]知

hr,t(n)=FHHr,t(n)F

(4)

式(4)中，F表示維數為Q×Q的FFT矩陣，矩陣中的元素可以表示為：

(5)

Hr,t(n)為Q×Q對角矩陣，其對角線上的元素為信道沖激響應的傅里葉變換：

(6)

建立系統的狀態空間模型是運用人工免疫濾波算法進行信道估計的關鍵。在MIMO-SCFDE系統中假設每對收發天線間的多徑信道相互獨立，且多徑數目相同。由文獻[15]知，可將時變信道建模為一階自回歸(AR)模型，為了減少計算量，只考慮第r個接收天線。

n時刻第r個天線的接收數據可以表示為：

Yr(n)=X(n)Hr(n)+Vr(n)

(7)

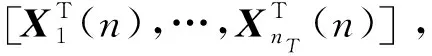
p(zn)=(1-ε)N(0,ξ2)+εN(0,κξ2)

(8)

式(8)中，0<ε<1，N(0,ξ2)的均值為0，方差為ξ2的復高斯分布，表示信道背景噪聲；N(0,κξ2)的均值為0，方差為κξ2，表示信道沖激噪聲。

對時變信道進行建模得：

Hr,t(n)=aHr,t(n-1)+zr,t(n)

(9)

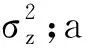
(10)

a=J0(2πfdts)

(11)

J0(·)表示零階Bessel函數，fd表示最大多普勒擴展頻移，ts表示采樣周期。將式(9)擴展到矩陣可得下式：

Hr(n)=AHr(n-1)+zr(n)

(12)

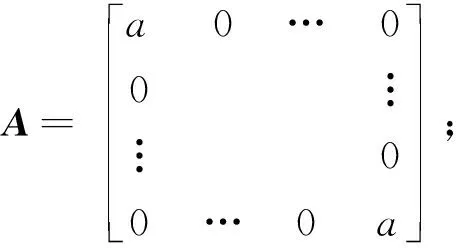
為簡化表達，將系統狀態空間表達式(7)和式(9)省去r，可以建立MIMO-SCFDE時變信道的狀態空間模型，如式(13)所示：

(13)

2 基于AIPF算法的信道估計

2.1 AIPF算法

人工免疫算法模擬了生物的免疫系統，在生物免疫過程中，抗體和抗原起主要作用，人工免疫算法將待求解的問題看為抗原，問題的某個解看作某個抗體，而抗體與抗原的匹配程度用親和力來描述。通過不斷地復制和變異，使得種群抗體親和力的分布較為均勻，此時的抗體即為最優解。

針對經典PF算法存在的權值退化問題，可以將人工免疫算法與PF算法相結合，依據粒子權值的大小對采樣的粒子進行變異處理，然后搜索最優粒子，迫使粒子集合向真實后驗分布概率較高的區域移動，從而間接地使取樣粒子的建議分布函數和真實后驗分布相似。

人工免疫粒子濾波算法的主要步驟如下：

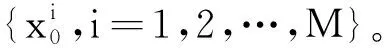
(14)

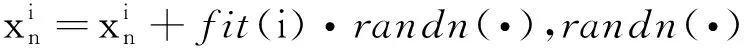
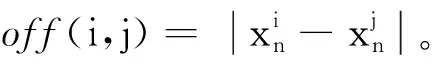
6) 重復步驟3)和步驟4)直到滿足某個結束條件。

7) 用最后得到的M個粒子估算出對狀態的估計值。

2.2 基于AIPF算法的信道估計實現

本文提出將人工免疫粒子濾波算法應用到MIMO-SCFDE系統信道估計中，以此提高系統信道估計性能。

上文中已經得到MIMO-SCFDE系統的狀態空間表達式以及AIPF算法的步驟，將利用AIPF算法進行信道估計的具體步驟總結如下。

步驟1)信道估計的初始化：

步驟2)從建議分布函數中采樣：

步驟3)當有新的觀測值時，通過觀測方程對權值進行更新：

步驟4)計算每個抗體的親和力以及抗體和抗體之間的排斥力：

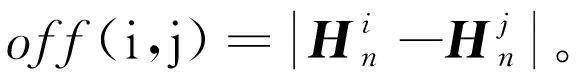
步驟5)克隆抗體，依據每個抗體的親和力對抗體進行克隆操作。

步驟6)變異：

步驟7)選優：

將變異后所有抗體的fitn(i)和offn(i,j)計算出，拋棄offn(i,j)<0.000 1中的一個抗體，并按fitn(i)進行排序，選出前面的M個抗體更新記憶單元，返回步驟4，直到滿足終止判據為止。

步驟8)重采樣：

步驟9)狀態估計輸出：

當n=n+1，返回步驟2)。

3 仿真結果與系統性能分析

用Matlab對所用算法進行仿真，采用2發2收天線，V-BLAST空時發射方案；頻率選擇性衰落與時間選擇性衰落同時考慮在內，參數由Jakes模型產生；歸一化多普勒衰減率fdts分別取為0.005，0.01和0.02，對應不同時變程度的信道；信源調制方式為QPSK，采樣的粒子數M=50。

圖3和圖4分別表示fdts取0.005，0.01和0.02時本文信道估計算法分別在加性高斯白噪聲和Middleton-A噪聲環境下的誤碼率(BER)性能。

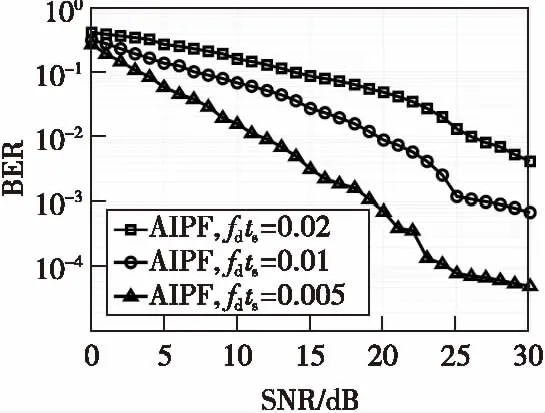
圖3 AWGN環境下，AIPF算法在不同fdts下BER比較Fig.3 The BER comparison of AIPF in different fdts when in AWGN envirenment

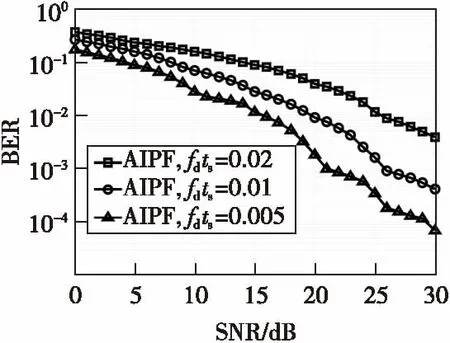
圖4 Middleton-A噪聲環境下，AIPF 算法在不同fdts下BER比較Fig.4 The BER comparison of AIPF in different fdts when in Middleton-A noise envirenment

由圖3、圖4可以看出，當歸一化多普勒衰減率增加即信道時變程度加劇時，系統BER增加，估計的精度降低。而圖4相比圖3，并沒有顯著變化，說明本文算法在非高斯分布噪聲環境下具有較好的頑健性。

fdts取0.01時，將本文算法，LS算法，Kalman濾波算法以及PF算法分別在AWGN和Middleton-A噪聲環境下應用于MIMO-SCFDE信道估計中，將其仿真結果進行比較。其BER性能和歸一化均方誤差(NMSE)如圖5—圖8所示。

圖5和圖6展示了在AWGN環境下四種信道估計算法的BER和NMSE，圖7和圖8展示了在Middleton-A噪聲環境下四種信道估計算法的BER和NMSE。可以看出，無論在哪種環境下進行時變信道估計，本文算法的BER性能和NMSE性能均好于其他三種算法。在Middleton-A噪聲環境，即非高斯分布噪聲環境下，用Kalman濾波算法進行時變信道估計時，其BER和NMSE性能不穩定，低于處在加性高斯白噪聲環境下的性能，說明Kalman濾波算法在非高斯分布噪聲環境下頑健性較差，而粒子濾波算法和本文算法均未受影響。

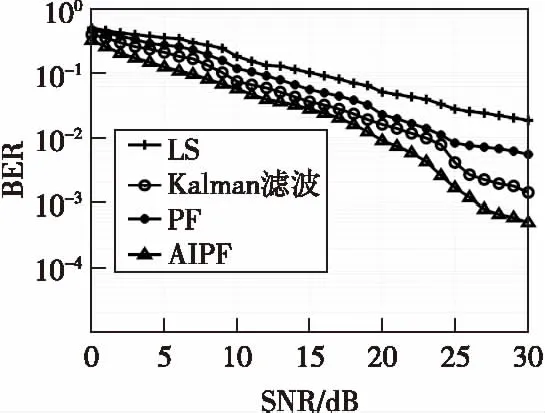
圖5 fdts=0.01時，AWGN噪聲 環境下四種算法BER比較Fig.5 The BER comparison among the four algorithms with fdts=0.01 when in AWGN noise environment

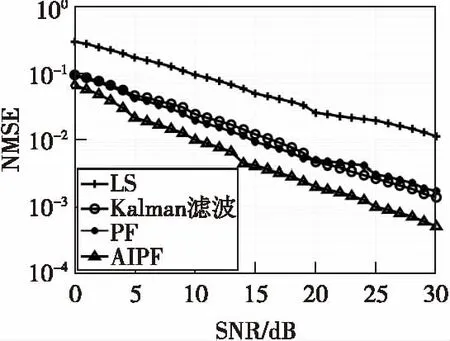
圖6 fdts=0.01時，AWGN噪聲 環境下四種算法NMSE比較Fig.6 The NMSE comparison among the four algorithms with fdts=0.01 when in AWGN environment

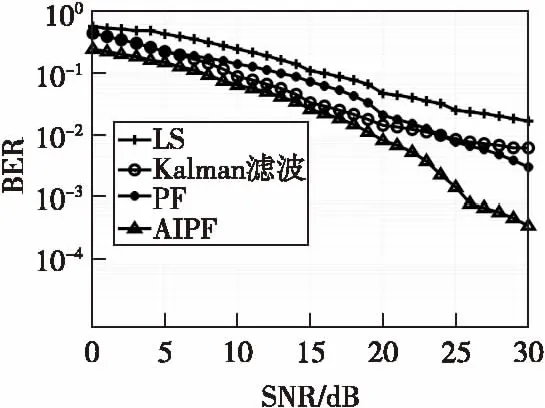
圖7 fdts=0.01時，Middleton-A噪聲 環境下四種算法BER比較Fig.7 The BER comparison among the four algorithms with fdts=0.01 when in Middleton-A noise environment

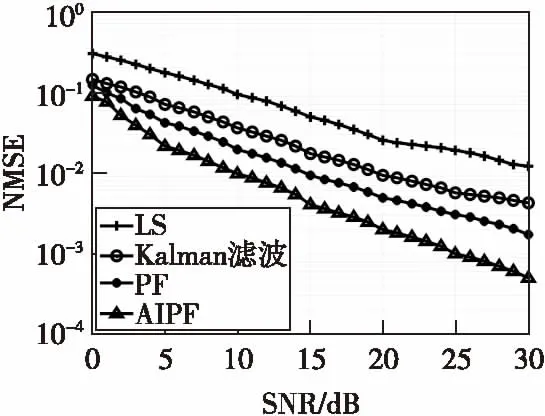
圖8 fdts=0.01時，Middleton-A噪聲 環境下四種算法NMSE比較Fig.8 The NMSE comparison among the four algorithms with fdts=0.01 when in Middleton-A noise environment

4 結論

本文提出了基于AIPF算法的MIMO-SCFDE系統時變信道估計方法。該方法將人工免疫的思想引入到PF算法中，有效緩解了PF算法權值退化的問題，提高了信道估計的精度。仿真結果表明，相比LS算法，Kalman濾波算法以及經典PF算法，AIPF算法在高斯分布噪聲環境以及非高斯分布噪聲信道環境下均可以得到較低誤碼率(BER)以及歸一化均方誤差(NMSE)，而且在非高斯分布噪聲環境下具有較好的頑健性，可以有效提高MIMO-SCFDE系統信道估計的性能。但AIPF算法過程較為復雜，如何在保持其性能的基礎上降低算法復雜度是下一步研究方向。