行進間粗對準誤差分析方法

王律化，石志勇，宋金龍，王海亮

(陸軍工程大學石家莊校區，河北 石家莊 050001)

0 引言

初始對準是確定慣性導航系統初始的姿態、位置、速度等導航參數。按照對準過程，分為粗對準和精對準兩個階段。為提高初始對準過程中載體的機動性，要求慣性導航系統能夠在載體行駛時完成粗對準過程。

針對上述問題，文獻[1]運用慣性空間為參考標準，分三步建立粗對準姿態矩陣。文獻[2—6]主要是利用里程計作為輔助測量手段，通過信息融合的方法解算姿態矩陣。文獻[7—8]將姿態矩陣的求解轉化為wahba問題，通過最優解的方法，解算姿態矩陣。

上述方法對于粗對準姿態矩陣的求解過程進行了詳細說明，但是鮮有文獻對粗對準過程中載體行駛速度、晃動角速度、加速度計零位偏差和陀螺常值漂移誤差與粗對準失準角之間的關系進行說明。

粗對準失準角的大小直接決定了后續精對準過程中所使用的誤差方程。因此，研究上述四個量和粗對準失準角之間的關系，對于行進間初始對準的研究，具有重要意義。針對此問題，本文在分析基于慣性系行進間粗對準方法的基礎上，提出了載體行進間粗對準誤差分析方法。

1 行進間粗對準算法原理

根據文獻[1]中的方法，行進間粗對準算法如下

(1)

(2)

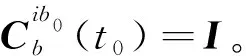
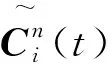
(3)

(4)

2 粗對準誤差分析

對于式(1)進行擾動得：

(5)

(6)

(7)

(8)

將式(6)—式(8)帶入式(1)，并且忽略二階小項，得：

(9)

由式(9)可知

(10)

(11)

對式(11)進行積分得：

(12)

(13)

式(13)中，

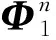
(14)

(15)

對式(4)進行變形得：

(16)

將式(14)帶入到式(16)中得

(17)

對比式(15)可得

(18)

所以

(19)

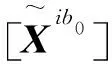
(20)

(21)

將式(20)代入到式(21)中，得到如下等式

(22)

(23)

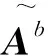
(24)

將式(24)帶入到xib0的等式中，得：

(25)

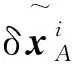
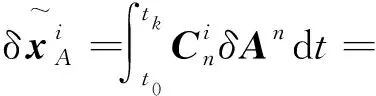
(26)

(27)

(28)

將式(12)帶入到式(28)中得

(29)

對于上式中的sin(ωietk)和cos(ωietk)運用Taylor展開，由于粗對準的工程中，所用到的時間較短，所以略去二階以上的項，得：

sin(ωietk)=ωietk

(30)

(31)

將式(30)和式(31)帶入到式(29)

(32)

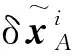
(33)

(34)

(35)

M=2[(cotL0An+Au)εe+cotL0Aeεn+Aeεu]

(36)

由于整個粗對準的時間較短，可以假設式(30)和式(31)中的sin(ωietk)和cos(ωietk)分別為0和1，

帶入到式(13)、式(34)和式(35)中得：

(36)

(37)

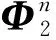
(38)

式(38)中，δAn=εeve-εuvu+ωeγe-ωuγu+n；δAe=-εevn+εnvu-ωeγn+ωnγu+e。

當載體處在靜止狀態時，式(38)轉變成下列等式

(39)

對比文獻[11]的結果和式(39)，在靜止的條件下，本方法的結果和解析法的結果相同。因為在解算載體行進間粗對準姿態矩陣時，其本質是雙矢量定姿原理，當載體處在靜止狀態時，不論是采用解析法還是基于慣性系的行進間粗對準，所能得到的極限精度應該是相同的。但是解析法粗對準只能使用于載體處在靜止狀態下，而基于慣性系的行進間粗對準可以在載體運動的條件下完成對準工作，因此有著更廣泛的應用前景。

3 仿真分析

載體在完成行進間粗對準的過程中，行駛速度、晃動角速度、加速度計零位偏差和陀螺常值漂移都對最終的對準結果有影響。為簡化分析，主要以不同條件下的東向水平失準角對準結果為例，對比各個條件對粗對準結果的影響。

3.1 速度影響仿真

假設載體總的運動時間為600 s，為驗證算法的有效性，進行100次的仿真。假設載體的初始位置為45.235 1°N/85.268 4°E，高度0 m，陀螺為激光陀螺，其常值漂移為0.015(°)/h，隨機漂移為0.001(°)/h，加速度計常值零偏為450 μg，隨機漂移為10 μg，里程計的刻度系數誤差為2‰，采樣時刻t1=60 s，t1=480 s，其載體速度分別為：2 m/s和6.5 m/s。仿真結果如圖1—圖2所示。

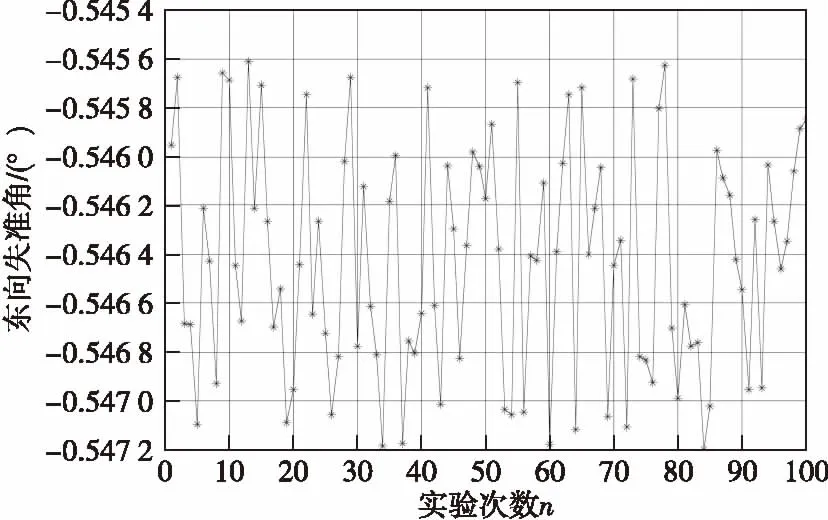
圖1 速度為2 m/s時東向失準角Fig.1 East misalignment angle when velocity is 2 m/s

圖2 速度為6.5 m/s時東向失準角Fig.2 East misalignment angle when velocity is 6.5 m/s

對比圖1和圖2仿真結果，當載體的運動速度從2 m/s變為6.5 m/s時，由于速度的改變，其東向失準角從-0.546 4°變成了-0.756 3°,由于速度變為了原來的3.25倍，使得失準角擴大了38.4%。可見由于載體在粗對準過程中速度的增加，使得對準的精度降低，因此，行進間粗對準的過程中，應當盡量降低載體的行駛速度，以保證對準精度。

3.2 載體晃動影響仿真

為檢驗載體晃動角度對于對準結果的影響，假設載體一直保持2 m/s的速度，載體晃動的角速度分別為1 rad/s和5 rad/s的仿真結果如圖3所示。

圖3 晃動速度為1 rad/s和5 rad/s時東向失準角Fig.3 East misalignment angle when waggle is 1 rad/s and 5 rad/s

通過對比載體在不同晃動角速度下東向失準角的仿真結果，發現東向失準角對于載體在不同晃動角速度下的變化不敏感。這說明基于慣性系的粗對準方法可以有效地隔離由于載體晃動所引起的對準誤差。

3.3 加速度計零偏影響仿真

為檢驗載體晃動角度對于對準結果的影響，載體的其他假設不變，速度保持2 m/s，同時假設加速度計的零位偏差從450 μg變為600 μg，仿真結果如圖4所示。

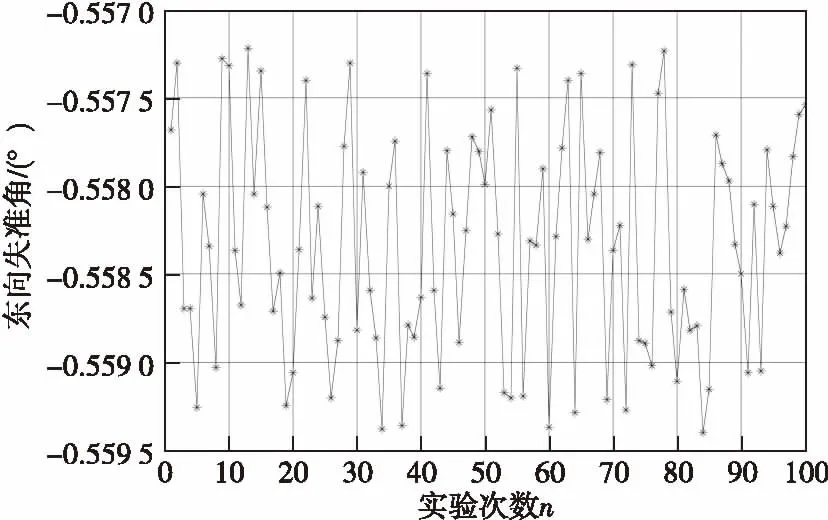
圖4 加速度計零偏為600 μg時東向失準角Fig.4 East misalignment angle with the accelerometer bias is 600 μg

對比圖2和圖4，當單純改變加速度計零位偏差的時候，東向失準角度數隨著零位偏差值的增大而增大，東向失準角的均值從-0.546 4°變為了-0.558 3°，加速度計的零位偏差增加了33%，其他條件不變的情況下，失準角度數擴大了2.18%。可見隨著加速度計零偏值的變大，對準結果中東向失準角的度數也在增大。

3.4 陀螺常值漂移影響仿真

為檢驗載體晃動角度對于對準結果的影響，載體的其他假設不變，速度保持2 m/s，同時假設陀螺的常值漂移從0.01(°)/h變為0.02(°)/h，仿真結果如圖5所示。

圖5 陀螺常值漂移為0.02(°)/h時東向失準角Fig.5 East misalignment angle with the gyroscope bias is 0.02 (°)/h

4 結論

本文提出了載體行進間粗對準誤差分析的方法，該方法在分析基于慣性系行進間粗對準方法的基礎上，以里程計作為輔助測量手段，通過微分擾動法，詳細分析了載體行駛速度、晃動角速度、加速度計零位偏差和陀螺常值漂移誤差與粗對準失準角之間的關系。仿真實驗表明，載體行進間粗對準的結果主要受到載體在進行粗對準過程中行駛速度和慣性測量器件本身精度的影響，而載體晃動對于對準結果沒有明顯影響。可見基于慣性系的行進間粗對準可以有效地隔離載體的晃動影響。同時，為提高粗對準的精度，在條件許可的情況下，可以降低載體的行駛速度以提高對準精度。