駐室傾斜對引信后坐針刺發火機構發火正確性的影響

王永亮，王雨時，聞 泉

(南京理工大學機械工程學院，江蘇 南京 210094)

0 引言

引信后坐針刺發火機構是一種經典的機械慣性發火機構，其主要原理是靠發射時的后坐力即直線慣性力使擊針相對火帽有足夠的戳擊動能戳擊火帽而使其發火。由于其結構簡單，目前仍廣泛應用于射彈引信系統。

引信后坐針刺發火機構設計過程中必須考慮兩點：一是在裝卸、運輸和裝填等勤務處理過程中滿足平時安全性；二是射彈發射時滿足發火正確性，即通常所說的“發火正確性”。典型的后坐針刺發火機構軸線設計與引信系統軸線是平行或重合的。但是在后坐針刺發火機構零部件、引信其他相關零部件和彈體等制造過程中，由于受徑向配合間隙以及垂直度等形位誤差的影響，往往導致引信后坐針刺發火機構駐室軸線相對于射彈運動方向出現偏歪，即產生一定角度的傾斜。

文獻[1]介紹了引信后坐保險機構相對于引信軸線斜置一定角度設置，可用來解決引信后坐保險機構安全與可靠解除保險之間的矛盾。文獻[2]以沖擊響應理論為基礎，分別對運動零件是擊針和火帽的兩種情況，提出了后坐針刺發火機構優化設計的數學模型，并且對算例中的引信后坐針刺發火機構提出了改進方案。文獻[3]指出由傳統設計方法——能量法設計的引信后坐針刺發火機構，其平時安全性和發射時的發火正確性不易得到保證，從而提出了概率設計方法，使機構平時安全性與發射時的發火正確性相互協調，以滿足規定的技術指標要求。文獻[4]在考慮機械引信后坐針刺發火機構結構尺寸、工藝、性能等要求的基礎上，建立了以最大安全落高和戳擊速度為目標函數的有約束非線性多目標函數最優化數學模型。文獻[5]列出了引信后坐針刺發火機構運動方程，并介紹了圖解分析法、余弦簡化法、直線簡化法、直接積分法和相面圖解法五種計算方法求得微分方程初值問題的解析解。文獻[6] 應用剛體動力學理論和仿真軟件ADAMS、LS-DYNA分析了引信經典彈性后坐保險機構和剛性后坐保險機構對不同后坐過載作用時間的響應特性，得到了不同后坐過載時間下兩類后坐保險機構解除保險時間響應。文獻[2—6]對引信后坐針刺發火機構進行的理論分析都是建立在其軸線與引信系統軸線平行或重合的基礎上，并未考慮其駐室傾斜對引信后坐針刺發火機構發火正確性的影響。針對此問題，本文借鑒文獻[1]的工作，通過理論分析和計算機仿真，提出駐室傾斜對引信后坐針刺發火機構發火正確性影響的計算方法，試圖為引信后坐針刺發火機構發火正確性分析和生產質量控制提供參考。

1 駐室未傾斜時引信后坐針刺發火機構慣性發火過程動力學分析

如圖1所示為炮彈引信后坐針刺發火機構。彈丸未運動時，擊針簧有一定的預壓量，其抗力作用于針刺火帽，針刺火帽另受螺塞的反作用力作用，處于平衡狀態。駐室未傾斜時，引信后坐針刺發火機構發火原理如圖2所示。在圖1和圖2所示的引信后坐針刺發火機構中，火帽在上，是相對運動件，而擊針在下，相對靜止。在實際應用中，還有另一類結構，就是擊針與火帽位置互換，擊針在上，發生相對運動，而火帽在下，相對靜止。但這兩類結構的力學原理和數學模型都是完全相同的。

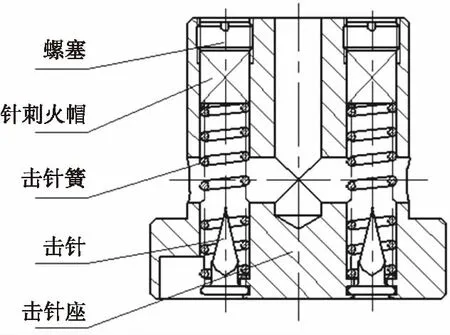
圖1 炮彈引信后坐針刺發火機構Fig. 1 An projectile fuze setback stab firing device

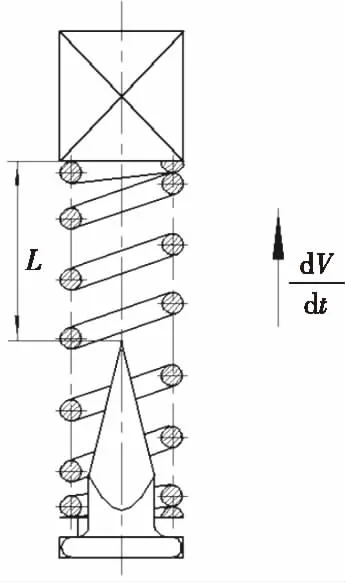
L-針刺火帽底端到擊針尖的距離；彈丸運動加速度 圖2 引信后坐針刺發火機構發火原理Fig. 2 The ignition principle of fuze setback stab firing device

彈丸在膛內加速運動時，在駐室未傾斜情況下引信后坐針刺發火機構的針刺火帽-擊針簧質量系統相對于擊針座暨引信體的運動方程為[7]：

(1)

式(1)中，x為針刺火帽相對擊針發生的位移；m為針刺火帽質量；m1為擊針簧質量；M為系統換算質量，是針刺火帽質量與擊針簧質量的1/3之和；x為針刺火帽在t時刻相對于后坐針刺發火機構(擊針座暨引信體)的位移；V為彈丸的運動速度；K為擊針簧的剛度系數；λ0為擊針簧的裝配預壓量；Ft為切線慣性力；Fc為離心慣性力；Ff為由切線慣性力Ft與離心慣性力Fc形成的駐室側壁摩擦力；f為針刺火帽與駐室內壁表面的摩擦系數。

(2)

對于旋轉彈引信和非旋轉彈引信，引信后坐針刺發火機構均在最大膛壓點之前工作結束。對于旋轉彈引信，研究保險機構意外解除保險特性時將Ff取為0系保守估計，故可以忽略。而在研究后坐針刺發火機構發火正確性時將Ff取為0則系冒進估計，故不宜采取。此時Ff由離心慣性力FC和切線慣性力Ft的合力將針刺火帽壓于駐室內壁而產生。由內彈道膛壓曲線和彈丸速度曲線的變化規律可知，在內彈道的起始階段，膛壓曲線的斜率較彈丸速度曲線的斜率要大，即膛壓上升得快，彈速增加得慢[5]。對于旋轉彈引信，引信后坐針刺發火機構在最大膛壓之前工作結束，這時彈速很小，離心慣性力Fc至少要比切線慣性力Ft小兩個數量級，因此計算時可以去除離心慣性力Fc且不影響計算精度，即不考慮離心慣性力Fc的作用。此時引信后坐針刺發火機構的針刺火帽-擊針簧質量系統的相對運動方程為：

(3)

式(3)中，ω為彈丸的旋轉角速度；r0為針刺火帽軸到彈軸的偏心軸。

式(3)可化簡為：

(4)

如果r0=0，則為中心配置的理想情況，此時無摩擦力。

直線運動后坐保險機構后坐保險件的運動方程與針刺火帽部件的上述運動方程完全相同。

2 駐室傾斜時引信后坐針刺發火機構慣性發火過程動力學分析

2.1 基于剛體動力學理論推導

假設引信軸線與彈丸旋轉軸線和速度方向重合，按照引信后坐針刺發火機構駐室軸線相對于彈丸旋轉軸線方位的不同，引信后坐針刺發火機構駐室軸線傾斜即與彈丸旋轉軸線不平行或不重合有多種情形，不同情形的傾斜對引信后坐針刺發火機構發火正確性的影響不同，且差異較大。駐室傾斜對引信后坐針刺發火機構發火正確性的影響主要取決于切線慣性力Ft和后坐力F沿駐室軸線方向的分力以及所形成的摩擦力。

如圖3所示，引信后坐針刺發火機構駐室軸線傾斜可根據駐室軸線、后坐力F和切線慣性力Ft是否在同一平面內分為兩種情形。傾斜方位、角度α和旋轉角速度一定時，后坐力F方向豎直向下、大小一定，切線慣性力Ft方向、大小一定，因此后坐力F和切線慣性力Ft的合力F2的方向、大小是一定的，F2與F形成的夾角β是一定的。此時駐室傾斜對引信后坐針刺發火機構發火正確性的影響取決于F2與駐室軸線之間的夾角角度大小，夾角越大，F2在駐室軸線方向的有效分力越小，對駐室內壁形成的正壓力越大，因此形成的駐室側壁摩擦力越大，對引信后坐針刺發火機構發火正確性的影響越大。當駐室軸線、后坐力F和切線慣性力Ft不在同一平面內時，傾斜角度α和F2與F形成的夾角β不在同一平面，此時F2與駐室軸線之間的夾角角度大小小于α+β；當駐室軸線、后坐力F和切線慣性力Ft在同一平面內時，傾斜角度α和F2與F形成的夾角β在同一平面，此時F2與駐室軸線之間的夾角角度大小等于α+β。因此當駐室軸線、后坐力F和切線慣性力Ft在同一平面內時，F2與駐室軸線之間的夾角角度最大，此時駐室傾斜對引信后坐針刺發火機構發火正確性的影響最為不利，如圖3(a)所示。

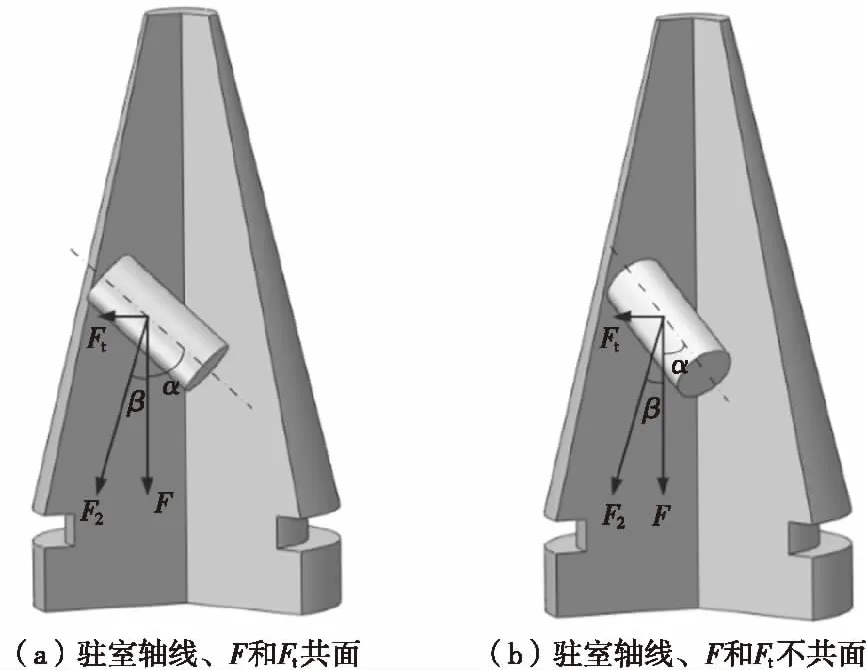
圖3 引信后坐針刺發火機構在彈丸發射時受到的力Fig. 3 The force of fuze setback stab firing device during the launch of the projectile

此時，針刺火帽受力特性如圖4所示。其中，F1為擊針簧對針刺火帽的彈性抗力，FN是駐室側壁對針刺火帽的正壓力。

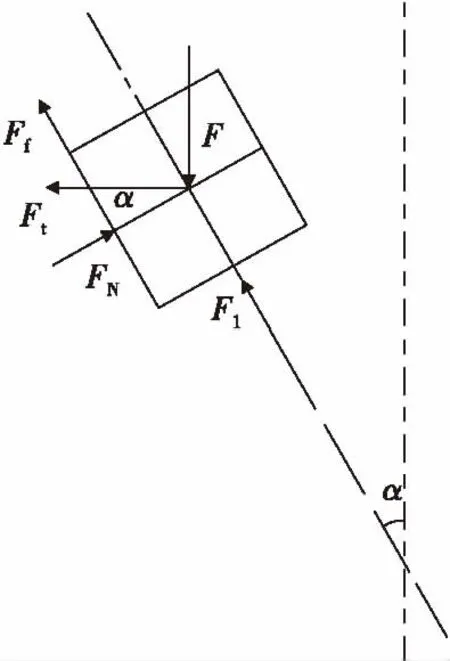
圖4 駐室傾斜最不利情況下針刺火帽受力特性Fig. 4 The force characteristics of stab primer in the worst inner cavity tilt case

彈丸未運動時，擊針簧有一定的預壓量，其抗力作用于針刺火帽，針刺火帽在螺塞的反作用力作用下，處于平衡狀態。

彈丸運動時，針刺火帽還會受到駐室側壁支反力(包括正壓力及其摩擦力)的作用，此時對針刺火帽進行受力分析，有

(5)

整理得引信后坐針刺發火機構的針刺火帽-擊針簧質量系統的相對運動方程為：

(6)

取α=0，則式(6)與式(4)一致，式(6)的正確性得到了驗證。

文獻[8]給出炮彈旋轉角速度ω和直線速度V的關系：

(7)

式(7)中，η為膛線的纏度。

(8)

則式(6)可化簡為：

(9)

對于一般的線膛炮彈引信，為了簡化分析計算過程，將膛壓曲線的上升段用余弦規律近似表達，即

(10)

式(10)中，P為內彈道所提供的膛壓，P0為擠進壓力；Pm為最大膛壓；tm為對應Pm的時間。

因此

(11)

式(11)中，D為彈丸的直徑；M1為彈丸的質量；φ為虛擬系數。

因此，式(9)化簡為：

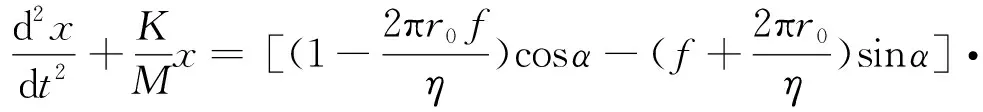
(12)

將式(12)化簡得：

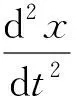
(13)

對式(13)求解得到：

(14)

利用初始條件：t=t0=0，x=0，dx/dt=0求出C1、C2并帶入式(14)得：

(15)

因此針刺火帽的速度表達式為：

(16)

取x=L，可求出從開始運動到擊針刺入針刺火帽深度為0時的運動時間tH和戳擊速度vH。為保證后坐針刺發火機構可靠發火，必須滿足[6]：

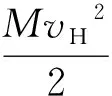
(17)

式(17)中，E=E0·exp(-0.1vH)，其中E為火帽100%發火所需的動態發火能量；E0為按標準條件

試驗時，火帽100%發火所需的能量。

2.2 算例分析

以37 mm口徑人工防雹增雨彈引信為例，計算駐室傾斜對引信后坐針刺發火機構發火正確性的影響。

由火炮內彈道學理論提供的斯魯豪茨基公式：

(18)

式(18)中，ωz為發射藥質量；φ0為阻力系數。

又由

(19)

式(19)中，γ為膛線的纏角，該37 mm口徑人工防雹增雨彈γ=5.88°。

已知該37 mm口徑人工防雹增雨彈引信后坐針刺發火機構設計參數如表1所列。

表1 37 mm口徑人工防雹增雨彈設計參數Tab.1 Design parameters of a 37 mm caliber artificial hail suppression and rainfall projectile

為了分別研究駐室傾斜角度α和針刺火帽與駐室內壁表面的摩擦系數f對引信后坐針刺發火機構發火正確性的影響，取f=0.25時，得到針刺火帽相對擊針的位移在不同傾斜角度α下與作用時間的關系，如圖5(a)所示；取α=5°時，得到針刺火帽相對擊針的位移在不同摩擦系數f下與作用時間的關系，如圖5(b)所示。

圖5表明：針刺火帽與駐室內壁表面的摩擦系數f一定時，針刺火帽運動相同位移所用時間隨著駐室傾斜角度α的增大而增大；駐室傾斜角度α一定時，針刺火帽運動相同位移所用時間隨著針刺火帽與駐室內壁表面摩擦系數f的增大而增大。因此，駐室傾斜角度α和針刺火帽與駐室內壁表面的摩擦系數f對引信后坐針刺發火機構發火時間均有影響。

取f=0.25，得針刺火帽相對擊針的速度在不同傾斜角度α下與作用時間關系，如圖6(a)所示；取α=5°時，針刺火帽相對擊針的速度在不同摩擦系數f下與作用時間的關系，如圖6(b)所示。

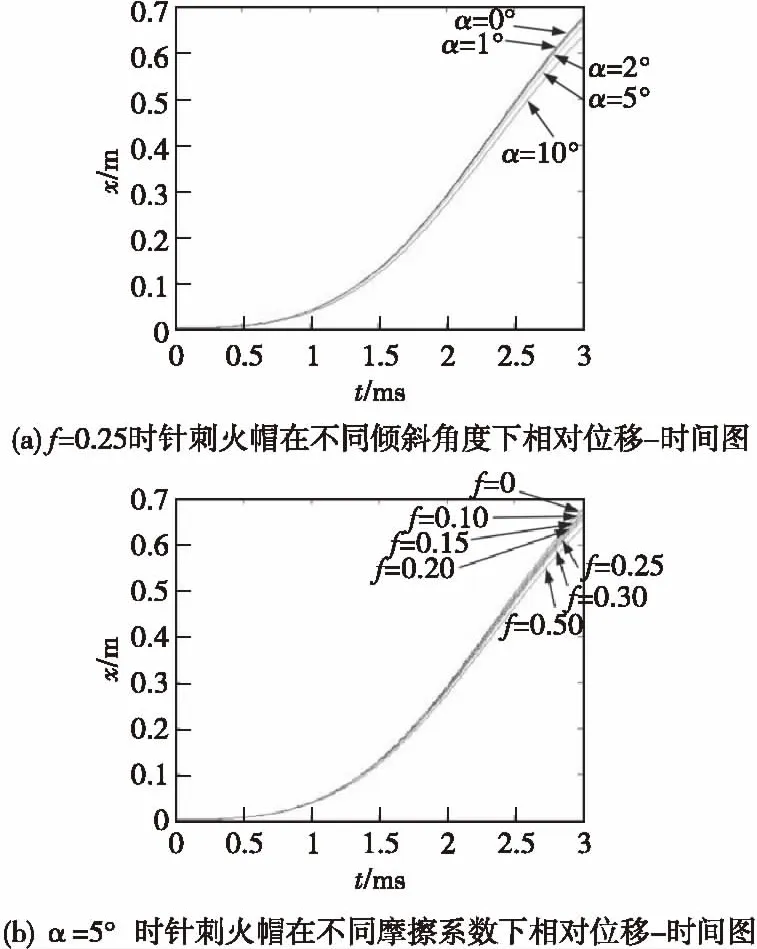
圖5 駐室傾斜時針刺火帽相對位移與作用時間關系Fig. 5 The relation between relative displacement and action time of stab primer with tilt inner cavity

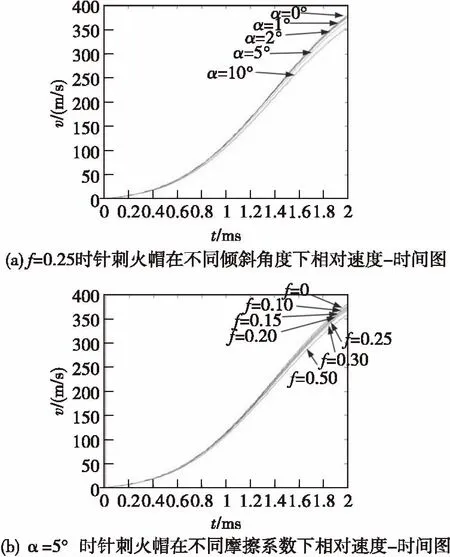
圖6 駐室傾斜時針刺火帽相對速度與作用時間關系Fig. 6 The relation between relative speed and action time of stab primer with tilt inner cavity

圖6表明，針刺火帽與駐室內壁表面的摩擦系數f一定時，針刺火帽在相同時間點的相對速度隨著駐室傾斜角度α的增大而減小；駐室傾斜角度α一定時，針刺火帽在相同時間點的相對速度隨著針刺火帽與駐室內壁表面的摩擦系數f的增大而減小。

該37 mm口徑人工防雹增雨彈針刺火帽底端到擊針針尖的距離L=6.25 mm，帶入式(15)得：

用MATLAB軟件求解得到針刺火帽與駐室內壁表面的摩擦系數f=0.25時，不同傾斜角度α下

針刺火帽從開始運動到擊針刺入針刺火帽深度為0時的運動時間tH，如表2所列。

表2 f=0.25時不同傾斜角度下 針刺火帽運動時間Tab.2 f=0.25, movement time of stab primer at different tilt angles

由表2得引信后坐針刺發火機構發火時間隨著傾斜角度的增大而增大。將上述數據帶入式(16)求出針刺火帽在不同傾斜角度α下的戳擊速度vH，如表3所列。

表3 f=0.25時不同傾斜角度下 針刺火帽戳擊速度Tab.3 f=0.25, puncturing energy of stab primer at different tilt angles

由表3得駐室傾斜時針刺火帽戳擊速度均小于未傾斜時截擊速度，不利于引信后坐針刺發火機構可靠發火。駐室傾斜會導致發火時間增大，即針刺火帽加速時間增大，同時駐室傾斜也會導致針刺火帽加速度減小，因此針刺火帽截擊速度變化取決于針刺火帽加速時間和加速度的變化量。

由文獻[8]知該引信所用針刺火帽按標準條件試驗時100%發火感度為1 000 g·cm，即E0=0.098 J，計算引信后坐針刺發火機構在不同傾斜角度下針刺火帽戳擊動能W、火帽100%發火所需的動態發火能量E和相對未傾斜時動能減少量ΔW，如表4所列。

表4 f=0.25時不同傾斜角度下針刺火帽戳擊動能和發火所需動態能量Tab.4 f=0.25, puncturing energy and the dynamic energy required for ignition of stab primer at different tilt angles

由表4得駐室傾斜角度α在[0，10°]區間內時，引信慣性針刺發火機構均能滿足針刺發火要求。

用MATLAB軟件求解得到駐室傾斜角度α=5°時，不同摩擦系數下針刺火帽從開始運動到擊針刺入針刺火帽深度為0時的運動時間tH，如表5所列。

表5 α=5°時不同摩擦系數下針刺火帽運動時間Tab. 5 α=5°, movement time of stab primer at different friction coefficient

由表5得引信后坐針刺發火機構發火時間隨著摩擦系數的增大而增大。將上述數據帶入式(16)求出針刺火帽在不同傾斜角度α下的戳擊速度vH，如表6所列。

表6 α=5°時不同摩擦系數下針刺火帽戳擊速度Tab. 6 α=5°, puncturing energy of stab primer at different friction coefficient

由表6得針刺火帽與駐室內壁表面的摩擦系數f不同，戳擊速度也不同，f=0時戳擊速度最大。摩擦系數的增大會導致發火時間增長，即針刺火帽加速時間增長，同時摩擦系數增大也會導致針刺火帽加速度減小。

計算引信后坐針刺發火機構在不同摩擦系數下針刺火帽戳擊動能W、火帽100%發火所需的動態發火能量E和相對摩擦系數為0.25時動能減少量ΔW，如表7所列。

表7 α=5°時不同摩擦系數下針刺火帽戳擊動能和發火所需動態能量Tab. 7 α=5°, puncturing energy and the dynamic energy required for ignition of stab primer at different tilt angles

由表7得駐室摩擦系數f在[0，0.35]區間內時，引信慣性針刺發火機構均能滿足針刺發火要求。

3 仿真驗證結果分析

為進一步探究駐室傾斜角度α和針刺火帽與駐室內壁表面的摩擦系數f對引信后坐針刺發火機構發火時間和戳擊動能的影響，與理論推導的結果對比，運用ADAMS軟件對引信后坐針刺發火機構傾斜時的運動特性進行仿真分析。根據結構尺寸和作用原理建立相應的仿真模型，該模型由螺塞、針刺火帽、擊針簧、擊針和擊針座組成，駐室未傾斜時模型如圖7所示。設置螺塞、針刺火帽、擊針和擊針座材料屬性，賦予其質量特性；設置彈簧屬性，給k、λ0賦值，給針刺火帽添加移動副，并在移動副上設置摩擦特性。對駐室不同傾斜角度進行仿真分析時，只需將圖7中螺塞、針刺火帽、擊針簧和擊針沿最不利傾斜方向傾斜預定角度重新建模即可；對針刺火帽與駐室內壁表面不同摩擦系數進行仿真分析時，只需改變摩擦特性中的摩擦系數即可。仿真分析時仿真參數與理論分析時各項設計參數相同。

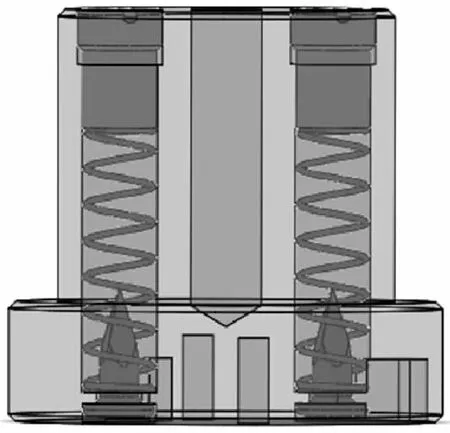
圖7 仿真模型Fig. 7 The simulation model

對針刺火帽與駐室內壁表面的摩擦系數f=0.25，針刺火帽相對擊針的位移L=6.25 mm時進行仿真分析，得到不同傾斜角度α對應的發火時間和戳擊速度如表8和表9所列。

表8 f=0.25時不同傾斜角度下發火時間Tab. 8 f=0.25, ignition time at different tilt angles

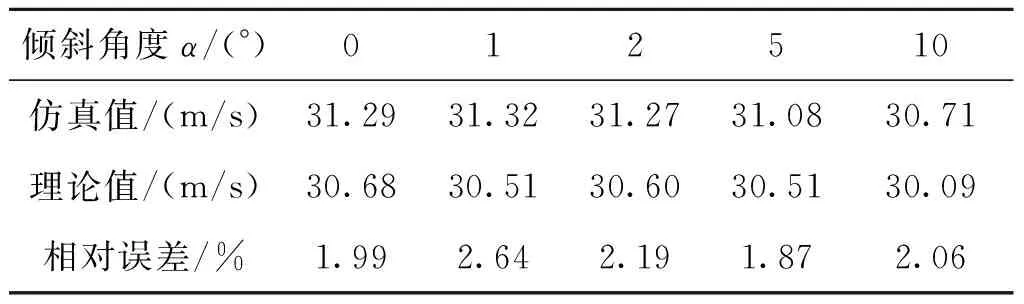
表9 f=0.25時不同傾斜角度下戳擊速度Tab. 9 f=0.25, puncturing energy at different tilt angles

分析表8和表9數據可得理論結果與仿真結 果比較接近，相差均在3%之內，證明了理論分析的可信性。驗證了駐室傾斜對引信后坐針刺發火機構發火時間和戳擊速度均有影響，但影響不大，可以忽略。

4 結論

本文提出駐室傾斜對引信后坐針刺發火機構發火正確性影響的計算方法。該方法建立了引信后坐針刺發火機構駐室傾斜時發火時間和戳擊能量的計算公式，并以37 mm口徑人工防雹增雨彈引信為例進行理論計算和仿真分析，仿真分析結果與理論計算結果吻合較好，驗證了理論計算公式的可信性。仿真分析和理論計算結果表明：引信后坐針刺發火機構駐室傾斜對發火時間和針刺火帽戳擊動能造成影響，但影響不大。仍以37 mm口徑人工防雹增雨彈引信為例，引信后坐針刺發火機構駐室傾斜10°、內壁與慣性體間摩擦系數0.25時，后坐戳擊動能降低3.9%。引信后坐針刺發火機構發火能量設計應考慮此裕量。引信后坐針刺發火機構駐室內壁與慣性體之間的摩擦系數一定時，發火時間隨著駐室傾斜角度的增大而增大，針刺火帽加速度隨著駐室傾斜角度的增大而減小，針刺火帽截擊動能的變化取決于針刺火帽加速時間和加速度的變化量；引信后坐針刺發火機構傾斜角度一定時，發火時間隨著駐室內壁和慣性體之間的摩擦系數增大而增大，針刺火帽加速度隨著駐室內壁和慣性體之間的摩擦系數的增大而減小，針刺火帽截擊動能的變化取決于針刺火帽加速時間和加速度的變化量。這些結論為研究引信后坐針刺發火機構發火時間和戳擊能量提供理論依據。