基于FP-growth算法的學生成績分析系統的研究

韓睿鵬，雷立宏，丁巖

（長春理工大學 計算機科學與技術學院，長春 130022）

隨著高等教育的迅速發展，大多數高校教育信息化的應用，教務數字化信息數量飛速增長，給高校管理機構和教師的教學方法的改進帶了不少新課題[1]。教育行業的大數據處理已經成為我們國家高校基礎性和前沿性的技術需求，對學生的成績數據進行深度的處理和分析就是一個亟待解決的課題，大數據基礎上的數據分析可以有效處理這一課題[2]。當前，大部分高校都具有學生成績數據的海量存儲，隱含在這些海量成績數據后面是很重要的知識信息，學生成績的大數據分析能夠挖掘并利用隱藏的價值。

1 數據挖掘技術及關聯規則概述

1.1 數據挖掘技術概述

在互聯網+時代，大數據的開放、挖掘和應用已經成為信息領域的發展趨勢。數據挖掘是在沒有確定目標下去發現潛在應用價值，數據挖掘與普通的數據處理不一樣，它把數據處理從簡單增添、刪除、查詢，提高到一個更高級的挖掘知識，智能決策階段[3，4]。數據挖掘的步驟如下圖1所示。數據挖掘任務實現的技術較多，從應用領域和科學研究方面考慮，數據挖掘的技術分為以下6種：關聯、預測、聚類、分類、回歸、診斷。

圖1 數據挖掘步驟

1.2 關聯規則概述

關聯規則分析方法是挖掘數據特征之間的彼此聯系，挖掘的目標是分析出數據之間隱藏的關系網[5]。關聯規則分析在許多領域獲得了良好的效果，例如商業、醫療保健、郵遞、金融證券等。關聯規則的基本概念如下：

定義1：關聯規則

關聯規則可表示為X?Y的公式，X，Y分別是項目集的真子集，X∩Y=?。X叫做X?Y的前提，Y叫做X?Y的結果。

定義2：關聯規則的支持度（Support）

關聯規則的支持度是交易集中同時包括X和Y的交易數與所有交易數之比，記為support（X?Y），即support（X?Y）=support（X∪Y）=P（XY）

支持度表明了同時包含X和Y的項集在事物數據庫中同時出現的概率。

定義3：關聯規則的置信度（Confidence）

關聯規則的置信度是事物數據庫中同時包含X和Y的事物數與所有包含X的事物數之比，記為confidence（X?Y），即：

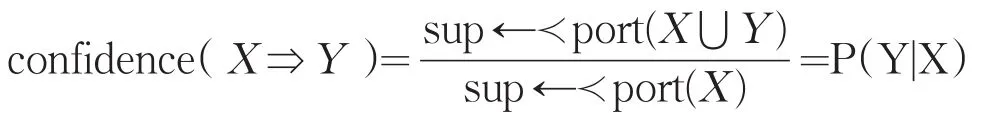
定義4：最小支持度與最小置信度

最小支持度（min_sup）和最小可信度（min_conf）都是用戶自己定義的一個界限值。X?Y的支持度≥min_sup并且X?Y的可信度≥min_conf，此時認為X?Y是有趣的。最小支持度描述項目集統計上最低重要水平，最小置信度描述了項目集統計上必需的最低可信性。

2 頻繁增長模式FP-Growth算法

2.1 FP-Growth算法定義

FP-Growth算法是一種關聯規則分析方法，創造性地提出使用更適宜的數型結構，沒有候選項目集，提高了算法的速度。FP-Growth算法主要分兩步：一、建立FP樹；二、從FP樹中挖掘頻繁模式[6]。該算法主要有以下兩大優點：一、不產生候選集；二、只需要2次搜索數據庫，效率很高。

該算法的具體描述如下：

第一步：FP-樹構造算法流程圖2所示。

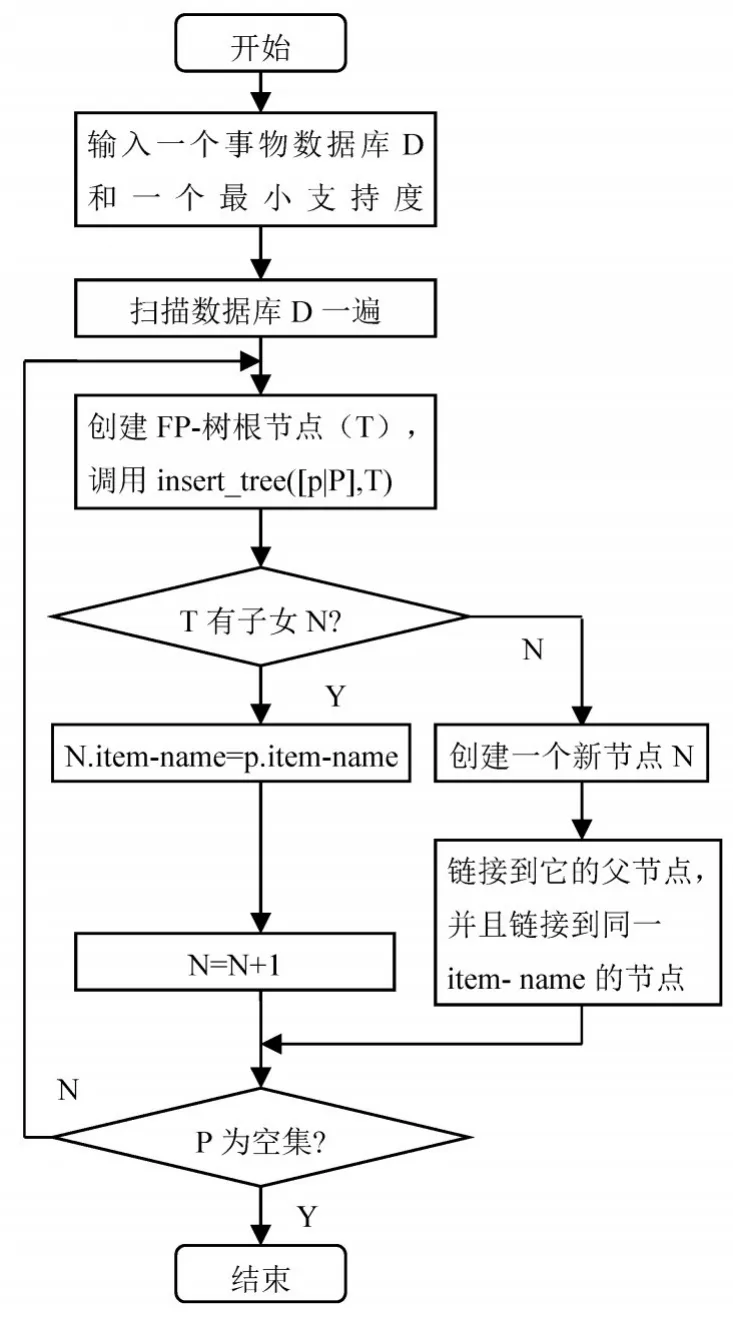
圖2 FP-樹構造算法流程圖

第二步：挖掘FP-tree的頻繁模式，算法流程圖如下圖3所示。

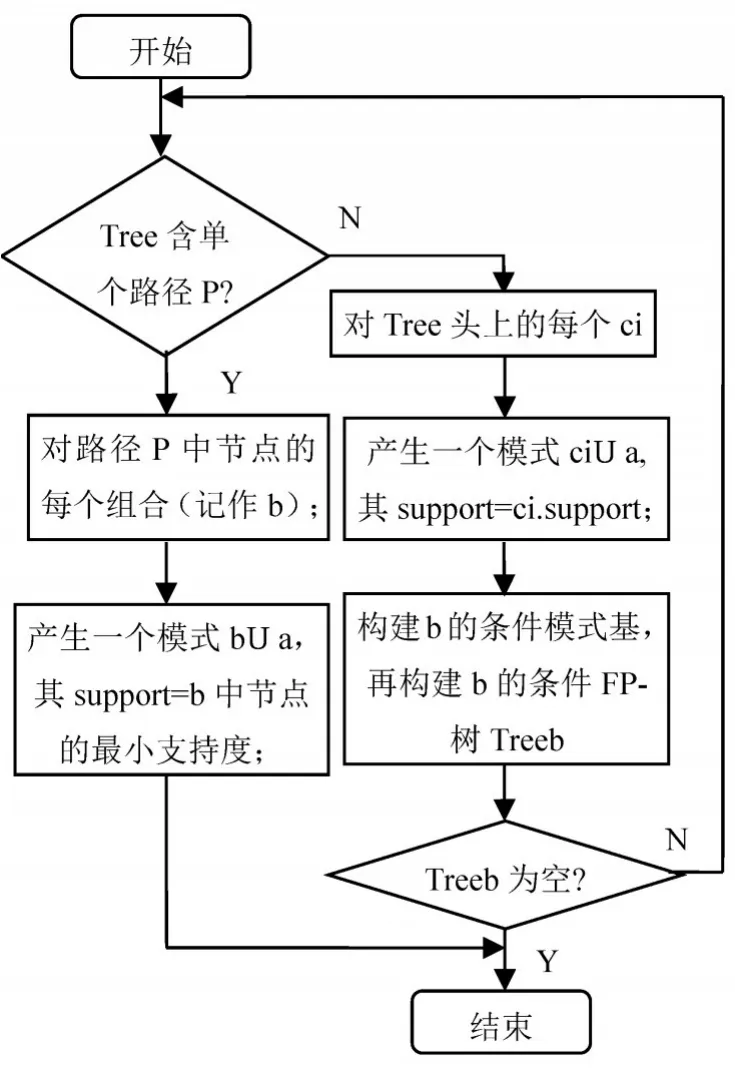
圖3 挖掘FP-tree的頻繁項集算法流程圖

2.2 FP-growth算法實例演示

為了說明算法的實現過程，假設原始項目集如圖4所示。

步驟1：構建FP-樹：

搜索事物數據庫，結果為頻繁集1-項目集F，如圖5所示。

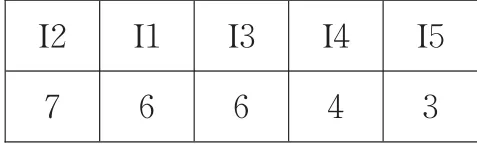
圖5 頻繁集1-項目集F

設定min_sup=2，對F重新排列，如圖6所示。

創建根節點和頻繁項目表如圖7所示。

圖7 根節點和頻繁項目表

加入第一個事物（I2，I1，I5）如圖8所示。

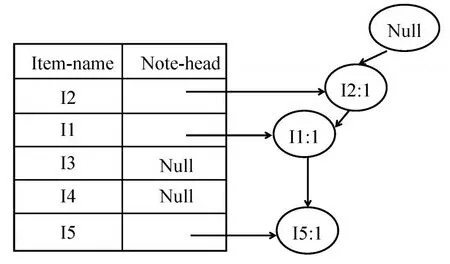
圖8 加入第一個事物的FP-樹

依次加入其它事物，一棵完整的FP-樹構建，如圖9所示。

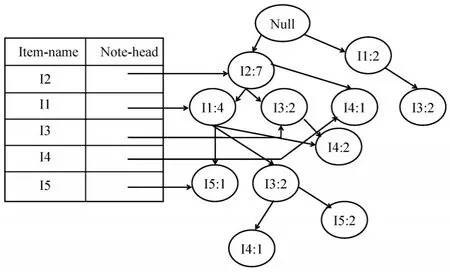
圖9 完整的FP-樹

步驟2：根據FP-樹挖掘頻繁項集：

1）首先從I5開始，導出條件模式基：＜（I2，I1，I3：1）、（I2，I1：1）＞，并構造條件FP-樹如圖10所示。

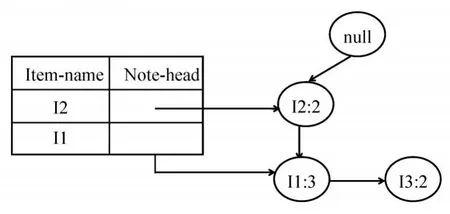
圖10 I5條件FP-樹

得到 I5的頻繁項集：{I1，I5：3}、{I2，I5：2}、{I1，I3，I5：2}、{I2，I1，I5：2}。

同理，依次考慮，I1，I3，I4，得到的頻繁項集如下。

I1的頻繁項集：{I2，I1：4}。

I3的頻繁項集：{I1，I3：4}、{I2，I3：4}、{I2，I1，I3：2}。

i4的頻繁項集：{I2，I4：3}、{I1，I4：2}。

上面實例演示了FP-Growth算法的詳細實現過程，可以看出，按照FP-Growth算法查找頻項集，更直觀，更高速。

3 基于FP-Growth算法的課程成績分析

3.1 數據準備及預處理

數據幾乎都是不完善的，大部分原始業務數據具有不完全，自相矛盾或數據噪聲等的一系列問題。數據預處理可以對原始數據進行糾正、篩選、合并、去除不合理的數據，從而提高數據質量，為下一步的數據分析做好準備。因為數據質量的差異，挖掘類型的不同，原始數據預處理運用的技術也會相應變化。一般情況下，數據預處理包括數據清洗、數據集成、數據規約和數據變換等步驟，如圖11所示。

用于成績分析的樣本數據來源于長春理工大學教務管理系統中2012-2016級計算機科學技術專業7個班4個年級必修課成績數據。教師輸入數字化成績時，偶爾也會出現失誤，學生也會由于某種原因缺考或中途退學，去掉成績缺失和數據錯誤的記錄后，共有1200條成績記錄。成績單包括學號、姓名、學院、系、計算機導論、面向對象程序設計、數據結構與算法、數字邏輯、計算機網絡、計算科學與數值方法等多個屬性。首先將姓名、學院、系這幾個屬性刪掉，其余的全部用于挖掘分析成績的屬性。

在數據分析前經常需要對連續型的數據進行轉換，數據離散化是創建數據挖掘算法最常使用的方法，而數據挖掘結果的可靠性是與數據離散化方法的選取息息相關的。數據離散化是把連續型數據劃分成若干區間，然后分別用不同符號來代替不同個區間。使用的是“自動調整寬度”的離散化方法。此方法的特點是充分照顧到不同數據特性，數值區間劃分的比例能夠調控，具有較強的靈活性[7]。

在針對學習成績的分析中，將分數制的成績數據離散化為等級制。由此把百分的成績分為優秀、良好、中等、及格、不及格5個等級，下表1表示各等級在各門課程中所占百分比[8]。

表1 課程成績離散化數據比例

依照表1中對各門課程成績的百分率分段，將每個學生的成績轉換成A，B，C，D，E五個等級。

3.2 代碼轉換表制定

把參加挖掘的每門課程名稱轉換為編碼，計算機導論的編碼為1，面向對象程序設計的編碼為2，數據結構與算法的編碼為3，以此類推[9，10]。

同樣把成績等級轉換為編碼，優秀為A，良好為B，中等為C，合格為D，不合格為E，則成績數據轉換后的代碼表如表2所示。

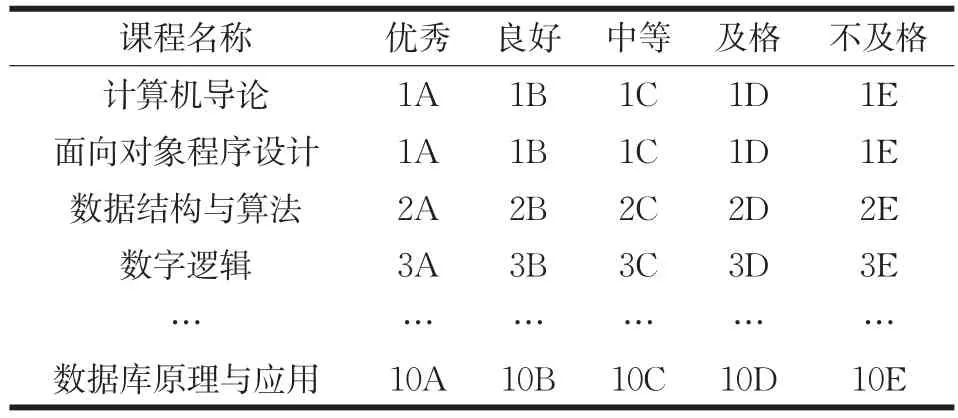
表2 代碼轉換表

3.3 學生成績表的轉換

學生成績數據庫如下表3，表中每一行是一個學生的成績信息，例如：第一行是學號S1的各門課成績，計算機導論、面向對象的程序設計、數據結構與算法、高等數學等分別是91、86、83、92、…。

表3 學生成績數據庫

依據FP-growth算法的要求，下面將學生成績數據庫（表3）轉換為對應的事務數據庫，使用區間映射方法，將學生表中對應的每一個的成績值由數值型映射成某個枚舉值，轉換結果如表4所示。

表4 事物數據庫

3.4 挖掘結果

為了數據挖掘的信息可信程度較高，設置min_sup=0.3，min_conf=0.6，執行 FP-growth關聯分析算法，分析哪些課程之間具有較強的關聯性，挖掘出前期課程對后期課程成績的影響。挖掘出來的部分結果如表5所示，可以看出，滿足最小支持度0.3的包含3門課的項集如下：

{數字邏輯（良好），面向對象程序設計（優秀），計算機網絡（優秀）}

{電工電子技術（優秀），數據結構（中等），計算機網絡（良好）}

{數據結構（良好），數字邏輯（良好），計算機網絡（良好）}

說明計算機網絡取得優秀成績和數字邏輯的優良程度且面向對象程序設計優秀具有很大的關系。

設置目標課程T為“計算機網絡”，目標規則為關聯后件包含“計算機網絡”的關聯規則。得到的關聯規則如表5所示。

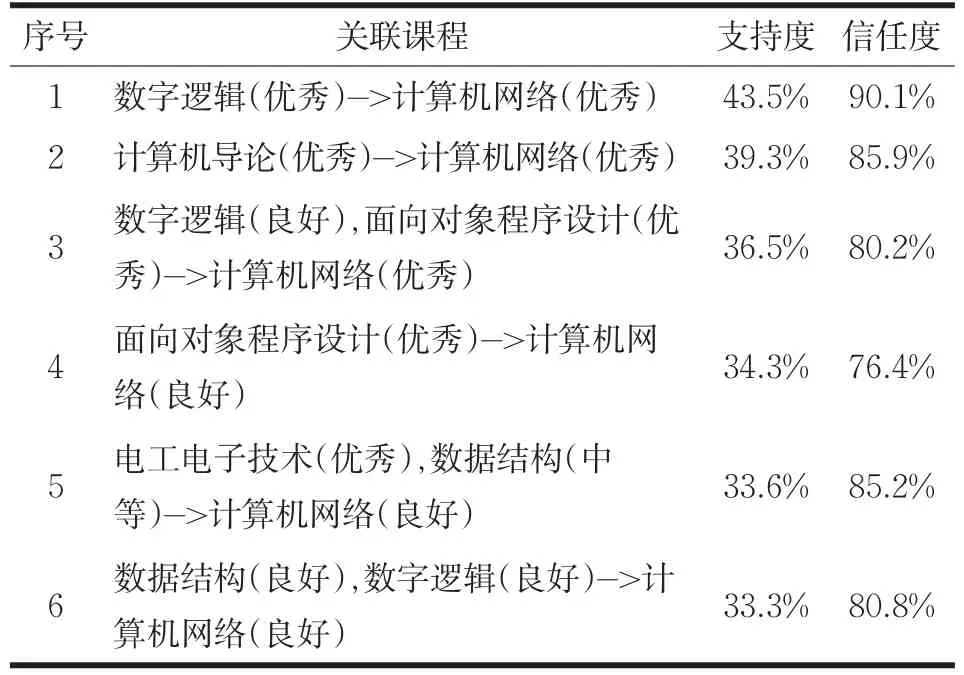
表5 部分挖掘結果示例

表5的規則表明如果數字邏輯成績優秀，則計算機網絡成績也為優秀的概率為90.1%，說明數字邏輯成績好的學生在學習計算機網絡課程時會有一定優勢，原因在于數字邏輯作為計算機專業的基礎學科，為學生奠定了邏輯運算及硬件基礎，可為學習計算機網絡打好基礎。計算機導論成績優秀，則計算機網絡成績也為優秀的概率為85.9%，說明計算機導論成績突出對學習計算機網絡也有很大優勢，計算機導論講述了有關計算機的基礎知識，基本理念，給予計算機網絡的學習很深厚的專業理論功底。同理，挖掘出的其他規則可以得到其他前期課程對計算機網絡成績的影響。

根據以上列出的具有較強關聯性的課程和推導出的關聯規則，教務管理人員可以預先了解學生學習有關課程的情況，有選擇性地制定教學計劃。例如，若計劃開設《計算機網絡》這門課程，則可使用《數字邏輯》這門課程學習成績對《計算機網絡》課程預先測評，對班級每個學生的學習狀況進行評估，根據不同的評估結果，分別對待，個別指導，繼而激發全班學生的學習潛力。學生們亦可根據挖掘出來規則，提高對某些課程的關注和努力。比如想要《計算機網絡》課程取得好的成績，從表5規則可看到，如果其先期課程《數字邏輯》成績良好及《面向對象程序設計》成績優秀，學好《計算機網絡》課程的可能性就很高，從為學習做好先期準備，提升學習效果。

4 結束語

關聯規則分析是數據挖掘中最簡單、最實用、最重要一種知識模式，實驗證明，通過FP-growth頻繁增長模式算法能夠有效地對課程成績數據進行挖掘分析，得到理想的挖掘結果。挖掘出來的關聯規則在某種程度上顯示了課程之間時間安排順序的重要性，前期課程對后續課程教學效果的影響力。此外，教師可以根據前期課程的學習情況，有目標、有針對性地對不同學生關注和輔導。學生也可參照規則，對學習的科目進行評估和預測，以便在今后的學習中采取有效的措施，最終達到較好的教學效果。課程成績數據分析的有效成果為將數據挖掘技術逐步推廣開來，應用在教育領域的各個方面，具有重要的現實意義。