基于改進LSSVM的節假日高速公路行程時間預測

李松江，宋軍芬，王鵬，楊迪

（長春理工大學 計算機科學技術學院，長春 130022）

高速公路作為現代化的交通基礎設施具有高速迅捷的特性，而節假日免費放行政策造成的交通擁堵嚴重擾亂了出行者的時間安排，因此，科學有效的交通預測方法成為了能夠有效緩解我國高速公路節假日交通擁擠的重要手段，而行程時間預測可以有效調節出行者的路徑選擇[1，2]，節省出行時間[3-5]。

在行程時間預測方法的研究方面，統計模型和智能化方法不斷被提出。李瑞敏等使用多源數據，建立了權重分配和神經網絡的數據融合模型對行程時間進行預測[6]。BUSTILLOS等結合N-Curve與KNN方法，提出了單近鄰與多近鄰的行程時間預測模型[7]。Wosyka等布設車牌識別系統采集車輛行程時間，建立決策樹模型預測行程時間[8]。Wang J等提出STDNN時空延遲神經網絡模型預測行程時間[9]。

上述預測方法中的樣本數據都需要依托采集設備完成，由于經濟狀況和高速公路的等級局限，導致數據獲取困難、信息缺失。而收費數據易獲取、質量高、實效性強，且能反映車輛行駛信息，因此本文采用獲取方便的收費數據，對節假日高速公路行程時間進行預測。

1 數據來源

以第一類客車（7座以下轎車、客車）的行程時間作為預測主體數據，實驗選取東北某省2012年至2015年高速公路部分路網法定節假日收費數據作為歷史數據集，以2016年S1路段（19.68km）數據作為測試數據，預測該路段的行程時間。首先統計車輛從收費站i到收費站j的進入時間和離開時間，然后按照公式（1）計算從收費站i至收費站j平均行程時間，時間間隔為15min。

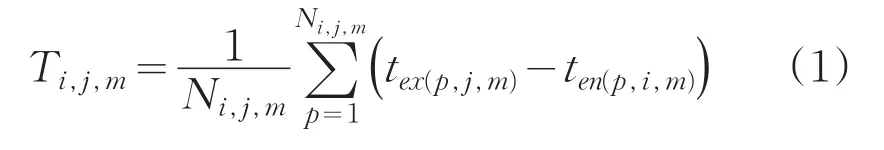
式中，Ni,j,m是時段m內駛入收費站i，駛出收費站j的車輛總數；tex(p,j,m)是樣本數據中第p條記錄中車輛駛入收費站j的時刻；ten(p,i,m)是數據中第p條記錄中車輛駛出收費站i的時刻。

2 數據分析及分類

以東北某省高速公路為例，對其節假日數據集按照行程時間分布規律集進行分類。

（1）清明節數據分析

統計2012年至2016年清明節時期某路段的客車數據，按照公式（1）計算行程時間，得到圖1的清明節期間行程時間的變化曲線。

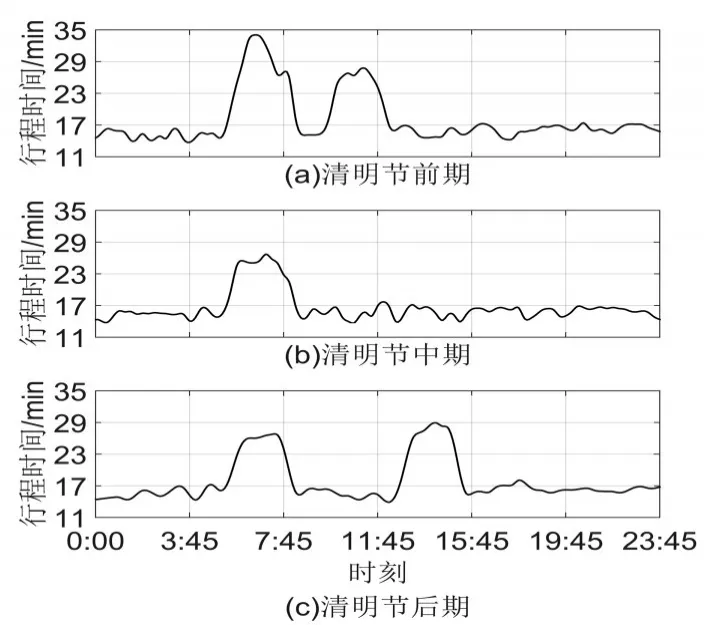
圖1 清明節行程時間變化

（2）勞動節數據分析

以2012年至2016年五一期間的客車收費數據為例，按照公式（1）計算行程時間，得到圖2勞動節前、中、后期的行程時間變化曲線。

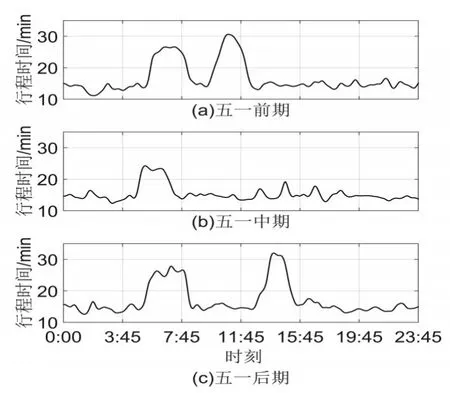
圖2 五一行程時間變化

（3）國慶節數據分析

統計2012年至2016年的收費數據，按照公式（1）計算行程時間，得到圖3國慶節期間行程時間的變化曲線。

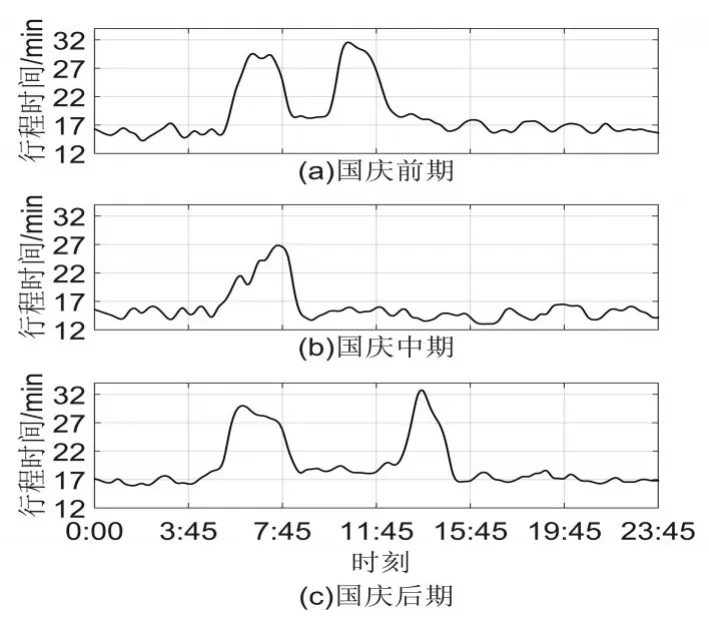
圖3 國慶節行程時間變化

（4）元旦時期數據分析

統計2012年至2016年這5年元旦期間的收費數據，按照公式（1）計算行程時間，得到圖4元旦前期、中期、后期行程時間的變化曲線。

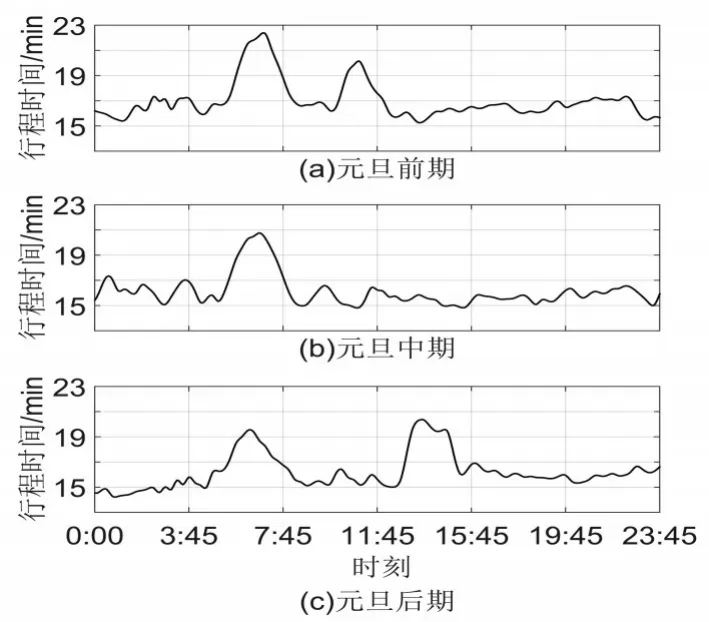
圖4 元旦行程時間變化

（5）春節數據分析

統計2012年至2016年這5年春節期間的收費數據，按照公式（1）計算行程時間，得到圖5春節期間行程時間的變化曲線。

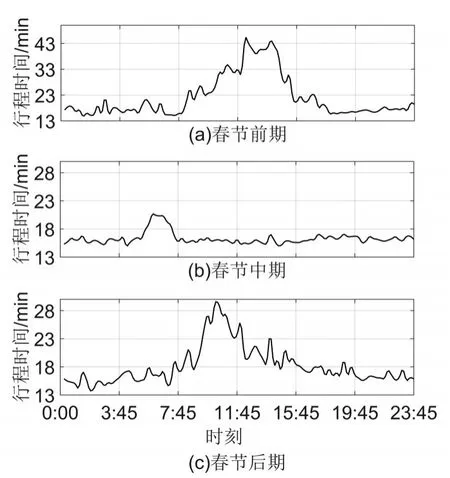
圖5 春節行程時間變化

通過上述對節假日數據的分布規律，將節假日歷史數據集分為5個子集：清明節、勞動節、國慶節、元旦的晨高峰和春節中期的晨高峰為一類；清明節、勞動節、國慶節、元旦前期的午高峰為一類；清明節、勞動節、國慶節、元旦后期的晚高峰為一類；春節前期和后期的高峰為一類；節假日的平峰為一類。

3 高速公路行程時間預測模型

3.1 最小二乘支持向量機

最小二乘支持向量機是一種以支持向量機為基礎的基于統計學理論的學習算法，使用最小二乘線性系統作為SVM算法的損失函數，將SVM中的不等式約束變換為等式約束，簡化了模型計算的復雜性，提高了求解速度。

對于給定的訓練樣本集T=(xi,yi)(i=1,2,…,n)，根據結構風險最小化原理，定義以下優化問題：

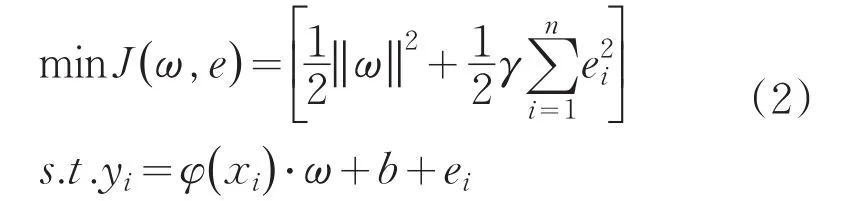
式中，ω為權重，γ為懲罰因子，ei為損失函數的松弛因子，b是偏置項。引入Lagrange函數解決上述優化問題：

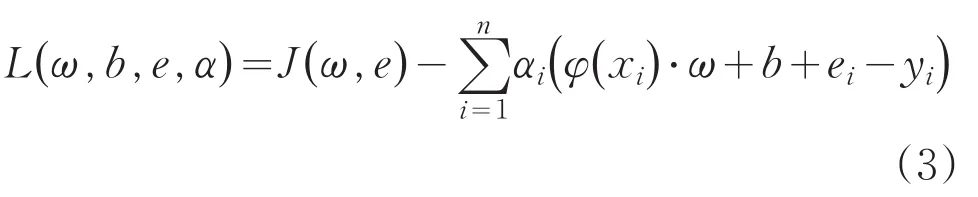
式中，αi為Lagrange乘子。對式（3）中參數求偏導為零，得到：

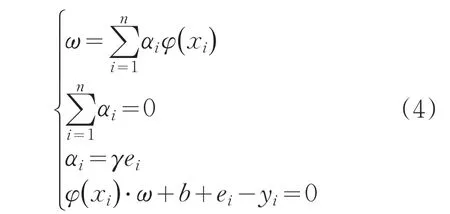
聯立求解方程組，得到LSSVM的回歸模型：

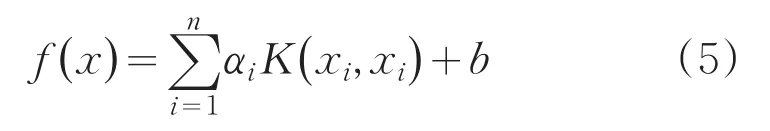
式（5）中K(xi,xj)為核函數。

3.2 構造核函數

在LSSVM模型中，為了更好的擬合，引入了核函數[10]，提高了模型的非線性處理能力，解決了維數災難問題。

經典的核函數分為全局核和局部核，它們性能差異較大，各有各的優缺點。目前的建模方法中一般采用單個核函數，然而這樣建立的模型預測精度并不高，為了使行程時間的預測更為準確，提出把全局核Sigmoid和局部核RBF結合起來，互補不足，形成一個性能良好的混合核函數，公式如下：

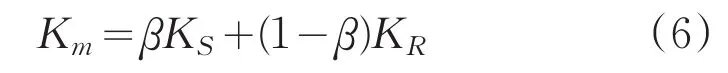
式中，Km為混合核函數；KS為Sigmoid核函數；KR為局部核函數；β為混合權重因子，用來平衡全局核和局部核對混合核的影響。根據Sigmoid核和RBF核的公式，公式（6）可變形為：

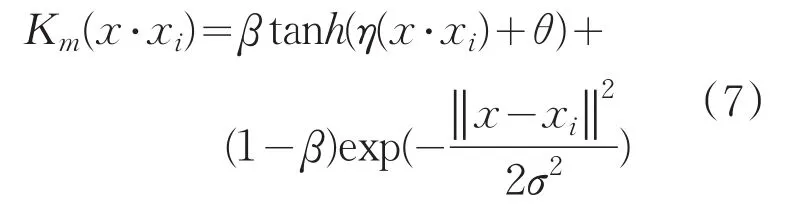
3.3 PSO算法

PSO粒子群算法是通過對一群隨機粒子的迭代尋找最優解，在每一次迭代過程中，粒子通過尋找個體最優值和全局最優值更新自身的速度和位置[11]。

假設在一個由N個粒子組成的種群的D維搜索空間中，粒子i在D維搜索空間中的位置為xi=(xi1,xi2,…,xid)，速度為vi=(vi1,vi2,…,vid)，粒子個體最優位置為Pi=(Pi1,Pi2,…,Pid)，粒子群體全局最優位置為Pg=(Pg1,Pg2,…,Pgd)，其中i=1,2,…,N。迭代中，粒子通過個體極值和全局極值更新自身的速度和位置，更新公式如下：

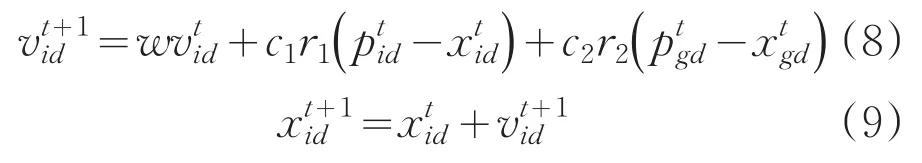
式中，vtid+1和xtid+1分別是粒子在t+1代的速度和位置；vtid和xtid為粒子在迭代t次后的速度和位置；w為慣性權重；c1和c2為學習因子；r1和r2是兩個隨機數，取值范圍為[0，1]。

傳統PSO算法收斂速度快，但是容易陷入局部極值，搜索精度不高，為了優化PSO算法，一些研究者對慣性權重和學習因子進行了改進。

（1）慣性權重是為了更好地平衡算法的全局搜索和局部搜索能力，當w值較大時，粒子的全局尋優能力強，不易陷入局部極值，反之，則局部尋優能力強，收斂速度快。基于此，研究者對w采用線性遞減策略，即：

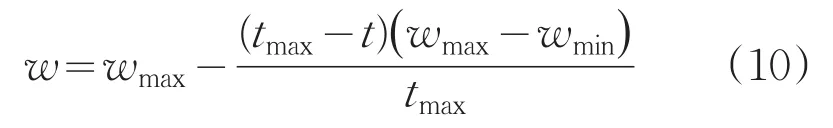
這樣雖然可以達到所需效果，但是也存在弊端，即在搜索前期如果無法找到最優值，那么在搜索的后期隨著權重的減小，很容易使算法快速收斂到局部最優。

（2）學習因子是用來調節模型學習的步長，公式（8）中第二部分為粒子自我認知部分，為社會經驗部分。當c1=0時，粒子失去了自我認知能力，只有社會經驗，這時粒子有擴展搜索空間的能力，具有較快的收斂速度，但容易陷入局部最優；當c2=0時，則粒子之間沒有社會信息，只有自我認知能力，這時由于粒子之間沒有信息的共享，整個粒子群相當于都在進行盲目的隨機搜索，收斂速度慢，以致于算法很難得到最優解。因此很多研究借鑒線性遞減策略的思想，對c1采用線性遞減策略，對c2采用線性遞增策略，即：

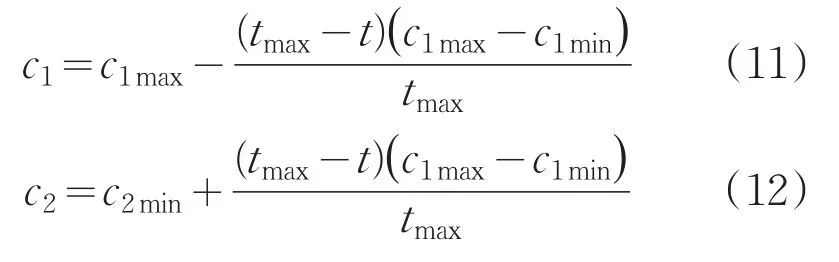
這樣雖然可以達到所需效果，但是也存在w一樣的弊端。

3.4 改進PSO算法

為了讓群體快速找到全局最優，本文將對PSO算法進行以下改進。

（1）二階遞減慣性權重

對慣性權重采用二階遞減策略，不但減少迭代次數，還降低算法陷入局部最優的概率，公式如下：

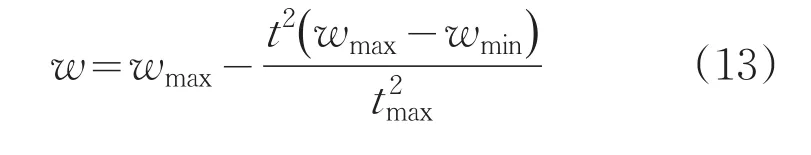
式中，wmax為最大慣性權重；wmin為最小慣性權重；t為當前迭代次數；tmax為算法最大迭代次數。

（2）二階異步變化的學習因子

對學習因子c1、c2分別采用二階線性遞減和二階線性遞增策略，公式如下：

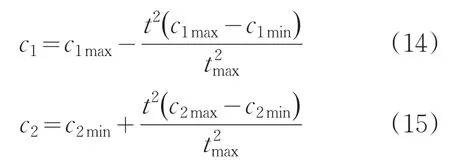
式中，c1max和c2min是學習因子c1和c2的最大值，c1min和c2min是學習因子c1和c2的最小值。

4 實驗分析

4.1 改進LSSVM模型參數設置

在預測行程時間之前，需要先設置模型的各個參數：設置γ∈[0 , 1000]；核函數σ∈[0 ,10]；Sigmoid參數η∈[0 , 10]，權重因子β∈[0 , 1]；種群規模N=30，最大迭代次數tmax=300，慣性權重w∈[0 , 1]，學習因子c1∈[0 , 2.5] ，c2∈[0 , 2.5]。

4.2 性能評價指標

采用定義均方根誤差（RMSE）、平均絕對誤差（MAE）與平均絕對誤差百分比（MAPE）評價預測結果的精度。

其中，TP(h)為h時段的預測行程時間；TA(h)為h時段的實際行程時間；Nh為預測時段數。

4.3 預測結果分析

選取2012年至2015年的節假日行程時間數據作為訓練數據集，以2016年的節假日數據作為測試數據集。

（1）數據集分類預測結果分析

按照第2節中介紹的分類方法對選取的訓練集和測試集進行分類，使用改進后的LSSVM模型對行程時間進行預測，以國慶節為例，得到圖6所示的國慶行程時間預測結果。

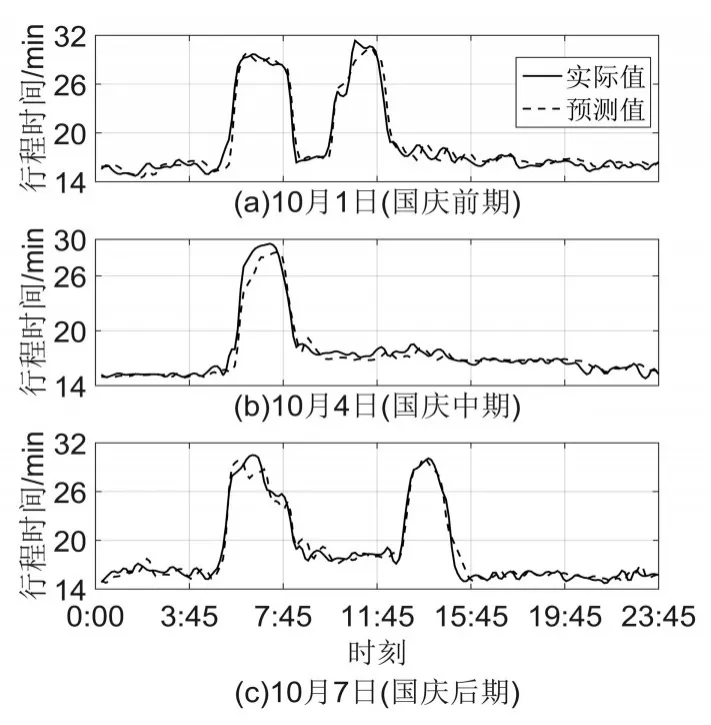
圖6 國慶節行程時間預測結果

從圖6可以看出，國慶各個時期的行程時間預測值的變化趨勢與實際值基本符合，表明對節假日數據集分類是可行的。為分析分類后預測模型的有效性和準確性，使用AMPSO-MK-LSSVM模型對未進行數據集分類的節假日高速公路行程時間進行預測。結果對比如圖7所示。

圖7 行程時間預測結果對比

由圖7可以看出：與未進行數據集分類的行程時間預測值相比，數據集分類后的預測效果更好，預測值與實際值更吻合。為體現數據集分類方法的預測精度更高，按式（16）-（18）計算RMSE、MAE和MAPE，結果如表1所示。

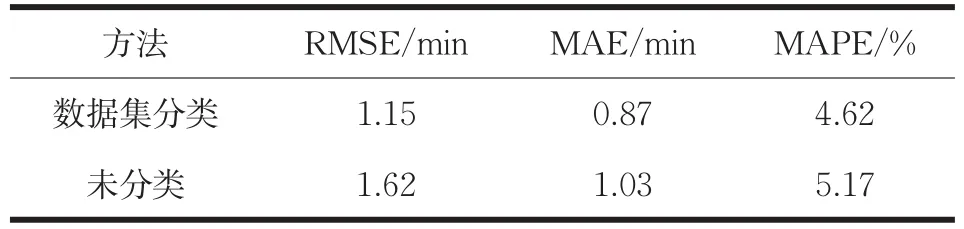
表1 兩種方法預測結果對比

由表1可以看出，數據集分類后模型預測的RMSE、MAE和MAPE與未進行數據集分類的模型預測結果相比均有一定程度的減少，其中RMSE降低了0.47，MAE降低了0.16，MAPE降低了0.55%。由此可見，對數據集分類提高了模型的預測精度。

（2）不同核函數預測結果分析

分別使用Sigmoid核、RBF核和MK核的AMPSO-LSSVM模型對10月7日路段行程時間進行預測，得到如下圖所示的預測結果。

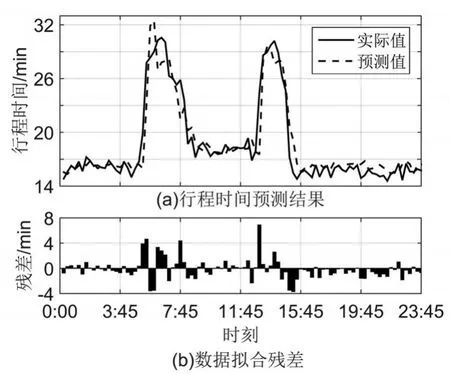
圖8 基于Sigmoid核的模型預測結果

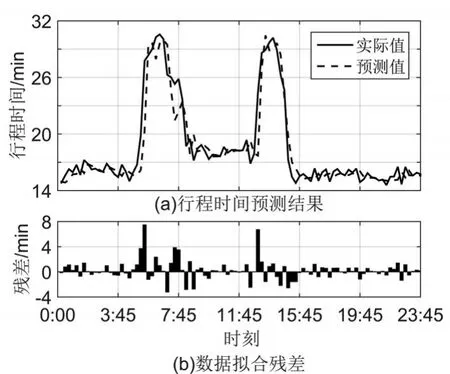
圖9 基于RBF核的模型預測結果

由圖8-圖10可以看出，基于混合核函數的AMPSO-LSSVM模型預測效果更好，預測值與實際值基本一致。而且Sigmoid核和RBF核的預測效果相差無幾，殘差范圍分別為[-3.68，6.87]、[-3.19，7.46]，但是混合核函數的AMPSO-LSSVM模型預測效果更好，殘差范圍僅為[-2.9，3.12]。由此看出：混合核函數涵蓋了全局核和局部核的優點，相對于單核核函數，使用混合核函數的AMPSO-LSSVM模型的預測效果顯著提高。

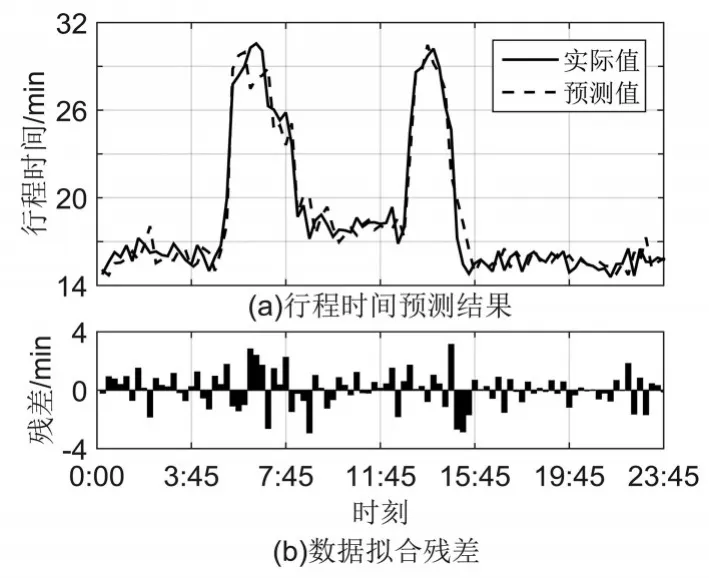
圖10 基于混合核的模型預測結果

（3）改進PSO算法預測效果分析

對比使用PSO-MK-LSSVM模型和AMPSO-MK-LSSVM模型的預測效果，在預測分析前先設置PSO-MK-LSSVM模型的各項參數：慣性權重w=0.9，學習因子c1=1.5，c2=1.7，其他參數設置同4.1節中設置的參數一致。改進PSO算法和標準PSO算法在參數尋優過程中適應度隨迭代次數的變化曲線對比如圖11所示。

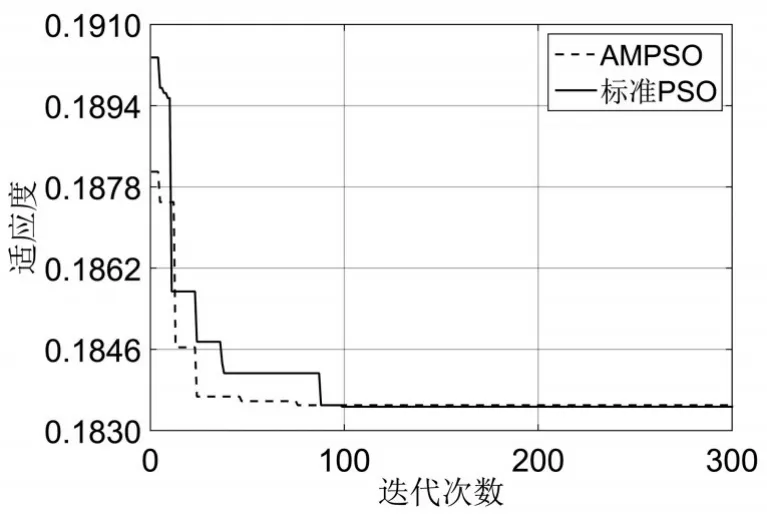
圖11 參數優化算法對比

由圖11可以看出AMPSO算法迭代至75次就趨于全局最優解，而標準PSO算法需要迭代至99次才能趨于最優解。為體現改進模型的預測性能，將其與PSO-MK-LSSVM模型進行對比研究，使用RMSE、MAE和MAPE作為評價指標，計算結果如表2所示。

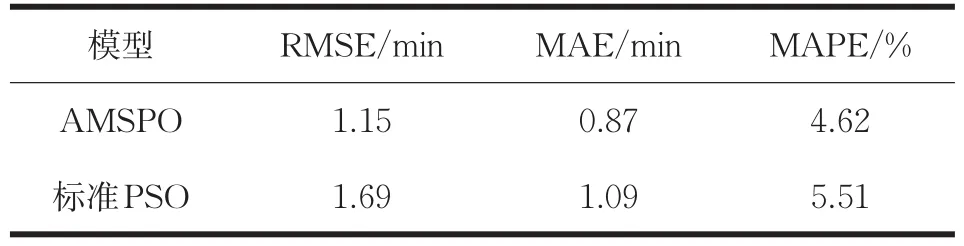
表2 兩種模型預測性能對比

由表2可以看出，改進模型預測的RMSE、MAE、MAPE值與傳統模型相比均有一定程度的減少，其中均方根誤差降低了0.54，平均絕對誤差降低了0.22，平均絕對誤差百分比降低了0.89%。由此可見，與標準PSO算法相比，改進的PSO算法有著較好的全局學習能力和局部學習能力，很大程度上改善了標準PSO算法早熟收斂的缺點，降低了迭代次數，加快了尋優速度，提高了預測精度。

5 結論

（1）提出對節假日數據集進行分類的方法，提高了模型預測的準確性。

（2）使用混合核函數代替LSSVM原有的單核核函數，提高了模型非線性處理能力，預測準確度有了很大的提升。

（3）使用改進后的PSO算法對預測模型的參數進行優化，加快了樣本訓練速度，提高了預測精度。