例談高三數學復習中如何培養學生核心素養
——以《隱軌跡問題》為例

戴天竹

（江蘇省蘇州實驗中學，江蘇 蘇州）

核心素養是知識、能力、態度或價值觀等方面的全面體現，它深深地影響著一個人的全面發展，高中數學教學中要努力發展學生的數學核心素養：數學抽象、邏輯推理、數學建模、數學運算、直觀想象、數學分析等能力。

高三復習課是對高中知識的提煉，是知識升華的一個過程，為高考服務，那如何有效提高課堂效率，如何引領學生形成核心素養，這一直是我們一線教師思考的問題。

本文以《隱軌跡問題》為例，談談本人對培養學生核心素養方面的一點想法。

一、課前熱身

1.已知圓 O：x2+y2=1，若直線上總存在點P，使得過點P的圓O的兩條切線互相垂直，則實數k的最小值為____.

2.已知 A、B 是圓 C1：x2+y2=1 上的動點P是圓 C2：（x-3）2+（y-4）2=1 上的動點，則的取值范圍是_______.

3.已知點 A（-2，0），B（4，0），圓 C：（x+4）2+（y+b）2=16，點P是圓C上任意一點，若為定值，則b=________.

評析：題1和題2中利用圓的切線、圓中弦、圓的直徑構造直角三角形便于問題的解決，通過這兩題讓學生能喚醒圓的相關知識，能總結到圓相關問題的解決，學會從圓的性質考慮解決策略。題3是阿波羅尼斯圓知識的簡單運用，此題的設計能讓學生喚醒阿波羅尼斯圓知識以及利用方程求軌跡的方法，從而為本節課打好知識儲備，以更好地提高學生的核心素養。

二、課堂分析

例1.已知圓O：x2+y2=5，A，B為圓O上的兩個動點，且AB=2，M 為弦AB的中點a+2）.當A、B在圓O上運動時，始終有∠CMD為銳角，則實數a的取值范圍為__________.

生：由M為弦AB的中點，可構造直角△OMA，故OM=2，所以當A，B在圓O上運動時，點M的軌跡為圓x2+y2=4，又由∠CMD為銳角，知點M在以CD直徑的圓外，所以圓x2+y2=4與以CD為直徑的圓（y-a-1）2=1 外離，所以 8+（a+1）2＞9，所以 a＜-2 或 a＞0.

師：這邊我們用到了哪些知識點？

生：圓中弦構造直角三角形，圓外的點對直徑的張角為銳角。

師：也就是說對兩定點張角為銳角的點在以此兩點為直徑的圓外，類似地，我們還能得到？

生：對兩定點張角為直角的點是以此兩點為直徑的圓，對兩定點張角為銳角的點在以此兩點為直徑的圓內.

變式：在平面直角坐標系xOy中，已知點P（-1，0），點 Q（2，1），直線 l：ax+by+c=0 其中 a，b，c 成等差數列，點P在直線l上的射影為H，則線段QH的取值范圍是__________.

生：由 a，b，c成等差數列，知直線 l過點 M（1，-2），又因為點P在直線l上的射影為H.所以點H的軌跡是以PM為直徑的圓x2+（y+1）2=8，所以線段QH的取值范圍是［

評析：此兩小題以多種形式體現對兩定點張角為直角的點是以此兩點為直徑的圓這一知識點，讓學生深刻地理解此知識點，并能升起挖掘隱含條件的強烈愿望，引導學生提煉問題的能力。

例 2.已知點 A（2，3），點 B（6，-3），點 P 在直線 3x-4y+3=0 上，若滿足等式A—→P·B—→P+2λ=0 的點 P 有兩個，則實數λ的取值范圍是__________.

生：設點 P（x，y），因為A—→P·B—→P+2λ=0，

所以（x-2）（x-6）+（y-3）（y+3）+2λ=0，即（x-4）2+y2=15-2λ，又因為點P有兩個，所以以上方程是圓，且與直線 3x-4y+3=0相交，所以所以 λ＜2。

師：我們注意到這里也有個圓，形成的方式和例1中不同，它是怎么形成的？

生：由向量點乘得到的。

師：能不能更準確點，把相關元素都一般化？

生：一個動點，兩個定點之間有某種向量點乘關系可能得到動點軌跡可能是圓。

變式：在平面直角坐標系xOy中，已知圓C：（x+1）2+y2=2，點 A（2，0），若圓 C 上存在點 M，滿足 MA2+MO2≤10，則點M的縱坐標的取值范圍是____.

生：設點 M（x，y），因為 MA2+MO2≤10，

所以（x-2）2+y2+x2+y2≤10，即圓面（x-1）2+y2≤4，

又點M在圓C上以及圓（x-1）2+y2=4與圓C的交點為（所以點M的縱坐標的取值范圍是

評析：此兩小題都是通過設點求軌跡的方法得到動點的軌跡方程。此處讓學生去尋找此類問題的共同點：都是有兩定點和一動點，進而由它們間的關系式得到動點的軌跡。通過對問題的總結，尋找共同點，提高學生總結問題、解決問題的能力，進一步提升學生的素養。

例3.在平面直角坐標系中xOy，已知圓C：x2+y2=5，過作點A（1，0）作兩互相垂直的直線分別交圓C于點E，F，G，H，則 EG 的最小值為 __________.

解析：本題可取EG中點B，根據圓中弦構造直角三角形，同時將兩動點間的距離EG轉化為AB，可得到動點B與定點O、A之間的關系，進而得到B點軌跡，再求出EG最小值。

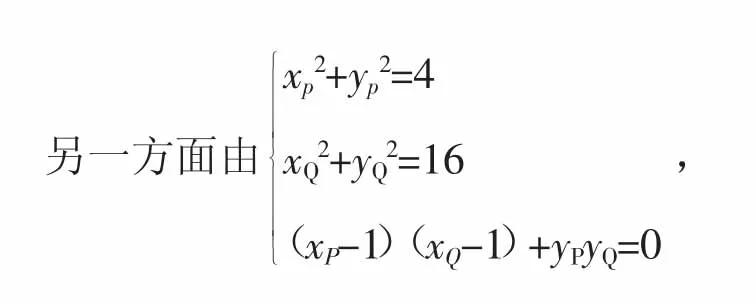
方法二：利用圓中弦構造直角三角形，如圖，延長PA交圓M于點P′，設O到PP′的距離為 d1，則（類似構造我們也可得到再由下同法一。可設 B（x，y）得所以AB的最小值為則EG的最小值為2.

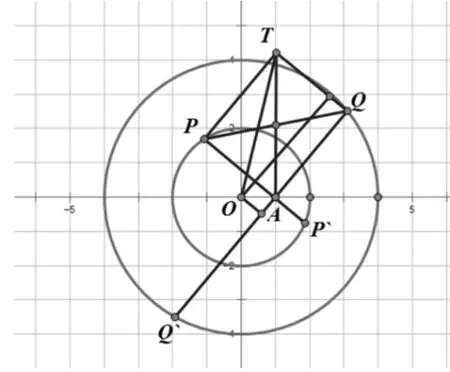
變式：已知圓 M：x2+y2=4，圓 N：x2+y2=16，點 A（1，0），動點P，Q分別在圓M、N上，且AP⊥AQ，則PQ的取值范圍為_________.

解析：方法一：將AP、AQ作為鄰邊作矩形PAQT（則有xT=xP+xQ-1，yT=yP+yQ），將求兩動點間距離PQ轉化為求一動一定兩點間距離AT，

評析：此兩小題體現化歸思想，將多動點問題轉化為一動點問題，進而用軌跡方程方法或圓中直角三角形等幾何法來求出此動點軌跡，進一步培養了學生邏輯推理、數學分析等核心素養，提升了學生解決問題的能力。

本文就高三復習課如何提高課堂效率、如何培養學生的數學核心素養進行了一些簡單的嘗試，今后還將進一步開發，將高三復習課打造成我們提高業務素養的又一基地。