速解三角函數不等式
——單位圓法

靳文嵐

（天祝藏族自治縣第二中學，甘肅 武威）

一、知識儲備

1.任意角三角函數的定義

利用單位圓定義任意角的三角函數.如圖1設α是一個任意角，它的終邊與單位圓交于點P（x，y），那么：

2.三角函數線

如圖1設任意角α的頂點在原點O，始邊與x軸非負半軸重合，終邊與單位圓相交于點P（x，y），過 P作 x軸的垂線，垂足為 M；過點 A（1，0）作單位圓的切線，它與角α的終邊或其反向延長線交于點T.于是有sinα=MP，cosα=OM，tanα=AT

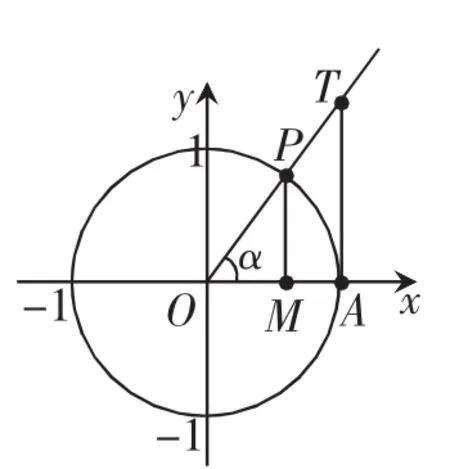
圖1

我們把這三條與單位圓有關的有向線段MP，OM，AT分別叫做角α的正弦線、余弦線、正切線。

二、解題原理——利用三角函數線解三角不等式

解：根據任意角三角函數的定義和三角函數線知識，sinα=y=MP，如圖2作直線交單位圓于P，Q 兩點，要或MP＞滿足條件的角α的終邊落在圖中射線OP，OQ分單位圓所成的上方弧所對扇形區域部分。

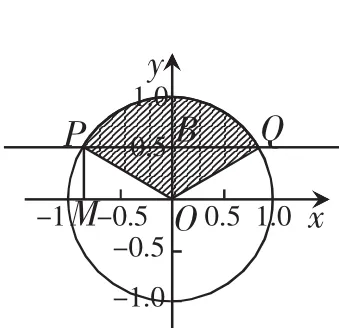
圖2

根據上述解法，若要解此類題型，需要求出終邊落在射線OP，OQ上角的集合，以及分析出所求區域為射線OP，OQ分單位圓所成的哪一部分便可，由此我們可以得到更簡潔快速的方法。

三、快速解三角函數不等式——單位圓法

例1.求滿足下列條件的α的取值范圍.

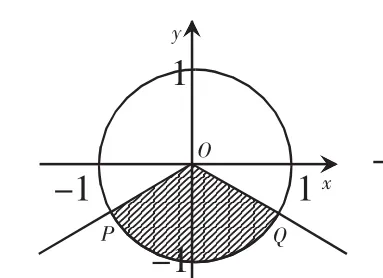
圖3

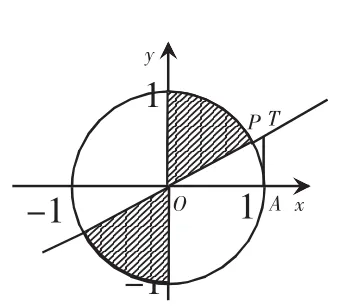
圖5

四、方法總結

滿足條件α的角的終邊落在被射線OP，OQ分單位圓所在區域為以下4種情況，其中a∈（-1，1），b∈R

sinα＞a，上方弧所對扇形；sinα＜a，下方弧所對扇形。

cosα＞a，右方弧所對扇形；cosα＜a，左方弧所對扇形。

tanα＞b，一四象限上方弧所對扇形及其對項角所在扇形。

tanα＜b，一四象限下方弧所對扇形及其對項角所在扇形。