小區開放對道路通行能力影響的研究
王朝陽,朱曉葉
(山東科技大學,山東 青島 266590)
1 評價體系的建立
1.1 評價指標的選取
通過查閱相關文獻,選取了具有代表性的四個指標來評價小區開放對周邊道路的影響,分別是道路通行能力、車輛平均速度、車流密度和交叉口平均延誤和。
車輛平均速度是指在交通流內部,車輛行駛速度的算術平均值,一般可以分為時間平均車速和區間平均車速,本文使用的是時間平均車速。計算公式為:

式中:n為交通流中車輛的數目;vi為第i輛車的瞬時速度。
車流密度是指在單位長度車道上,某一時刻分布的車輛數。計算公式為:

式中:N為長為L的道路在某一時刻存在的車輛數;L表示該路段的長度。
交叉口平均延誤時間是指車輛在交叉口處由于等待綠燈、堵車等原因而消耗的時間。計算公式為:

式中:T為信號燈的周期;tg為一周期內車輛能以飽和流率通行的時間;x為飽和度。
道路通行能力是指道路的某一斷面在單位時間內所能通過的最大車量數。計算公式為:
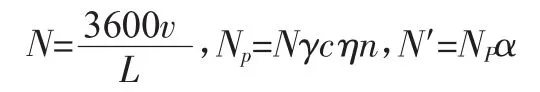
式中:N為基本通行能力;L為車頭間距;v為車速;Np為可行通過能力;γ、c、η、n分別為自行車影響修正系數、交叉口影響修正系數、車道寬度修正系數、車道數修正系數;N′為實際通行能力,α表示道路分類修正系數。
1.2 評價指標的權重分配——基于熵權法
考慮到指標權重的合理性,本文采用熵權法來確定權重。熵權法是一種客觀的賦權方法,它是利用各指標熵值所提供的信息量大小來決定指標權重的方法。計算步驟如下:通過調查某小區不同時間段四個指標的具體數值,得到原始數據矩陣X;對原始數據進行無量綱化處理;計算第i個對象在第j個指標下的特征比重和第j個指標的熵值;計算差異系數,確定各指標的熵權值。用MATLAB編程實現上述過程,得到這4個指標的權重系數如下:車輛平均速度系數W1=0.168;車流密度系數W2=0.213;交叉口平均延誤時間系數W3=0.220;道路通行能力系數W4=0.398。
2 小區道路通行能力模型的構建
2.1 路段通行能力計算模型
如果采用交通流中的跟車理論來建立車頭間距與車輛行駛速度之間的數學關系模型,要比直接用宏觀的車流模型更切合實際,因此本文用跟車理論分析道路路段的通行能力。結合跟車理論,在保證較高精度的前提下,得出小型車車頭間距與車速的關系為:

式中:v為車輛行駛速度;hs為車頭間距。由于hs=vht(ht為車頭時距),于是可以得出城市道路路段車輛的理論通行能力為:

對于普通的道路,可以認為,車輛受到路旁的干擾逐漸增大時,車速下降的速度會隨之加快,從而導致通行能力的下降,因此路旁干擾系數可以通過計算車速下降得到。也就是說干擾系數ε=va/vb,其中va為受到干擾后的車速,vb為沒有受干擾的車速。本文研究不受機動車和行人干擾的車道,這種情況下路旁干擾系數ε=1。
在設計道路時,有必要運用服務水平的概念來設計通行能力,即設計通行能力應該使道路達到某種服務水平,則設計通行能力為:

式中:Cap為相應于設計車速下的理論通行能力;v/c為相應于某一服務水平下的道路飽和度;ε為路旁干擾系數;ω為路寬修正系數;γ為側向凈寬修正系數。
2.2 信號交叉口通行能力計算模型
由文獻[3]可知,在已經配定定時式紅綠燈燈色的前提下,車輛通過交叉口一個沖突點的通行能力為:
式中:αm為由于穿越空檔導致的損失時間;β為有、無專用左轉車道時的得失時間;m為進口道中直行車道的條數。
3 小區開放對道路通行影響的實例計算
3.1 研究方法
本文選取小區內部的結構作為主要因素,應用第2部分建立的路段與交叉口通行能力的模型,定量比較內部結構存在差異的小區開放前后對道路通行的影響。針對不同道路結構的小區,共列出3類模型進行定量計算與對比分析,各類小區的結構如圖1所示。

圖1 三種小區結構簡圖
基于實際情況,采用將路段通行能力和交叉口通行能力線性加權的方法來計算小區的通行能力,即y=λ1Cd+λ2n。
其中,λ1為路段通行能力的權重系數;λ2為交叉口通行能力的權重系數。
3.2 仿真分析
基于上述思路,利用MATLAB軟件分別編寫路段通行能力和交叉口通行能力的函數,將車輛行駛速度、小區車道數目、道路修正系數以及道路飽和度作為輸入參數,并取不同的權重,對選取3個小區分別進行仿真分析,得到的結果如下。小區1:開放前通行能力為240.55,開放后為480.87;小區2:開放前通行能力為360.59,開放后為841.39;小區3:開放前通行能力為600.97,開放后為480.79。
由此可知,盡管小區1和小區2的內部結構不同,但是開放后產生了較好的結果,因此適合開放。分析二者的道路結構可知:小區1內部道路是樹狀的,開放后出入口數量明顯增多,可以顯著提高路網的密度,由此產生積極的影響;小區2內部道路比較寬,并且經過一些道路可以直接到達外界,道路結構簡單,開放后可以有效緩解交通壓力。而對于小區3,開放后通行能力明顯下降,觀察小區結構可知:其內部道路很窄,且道路多為環狀,有些道路在小區內直接中斷,無法與外界道路連通,即使開放也不會產生很好的效果,因此不適合開放。

