多元情境多重體悟多維建構
———《認識方程》教學案例（一）

鮑善軍

【教學內容】

人教版五年級上冊第62、63頁。

【課前思考】

“認識方程”是學習代數的基礎，是在學生熟悉了常見的數量關系，能夠用字母表示數的基礎上進行教學的，其內涵豐富而抽象。如何讓學生順利地從算術思維過渡到代數思維？如何讓學生真正感受到方程的內在本質？這些都需要深入思考。

方程的本質是什么？簡單地說，就是左右兩邊相等，這不僅是方程概念的本質，也是列方程解決問題的依據。陳重穆教授曾撰文呼吁：“含有未知數的等式叫做方程”這樣的定義要淡化，不要記，無須背，更不要考。關鍵是要理解方程思想的本質，它的價值與意義。張奠宙教授對方程重新定義：“方程是為了尋求未知數，在未知數和已知數之間建立起來的等式關系。”可見，“含有未知數的等式叫做方程”并非方程的嚴格定義，僅是一種樸素的描寫，方程的意義不在于概念本身，而在于方程的本質特征：要“求”未知數，在未知數和已知數之間建立起來的等式關系。

如何建構方程的意義？方程是一種工具，是一種現實模型，它能幫助我們很好地解決問題。教師引導學生建立方程模型，首先要為學生提供一個生動具體的現實情境，便于學生通過觀察、比較，從中抽象出數學問題，并用簡潔的數學語言進行描述。借助天平稱物這一具體情境，抽象出數學式子，然后通過現實情境，找出兩種事物的等量關系，學生逐步擺脫天平的表象，在數學問題中尋找“心中的天平”，在經歷建模的過程中逐步鞏固加深對方程概念的理解和應用。

方程思想的核心在于建模和化歸，即依據等量關系列方程和依據等式性質解方程。學生在問題情境中探索、研究，尋求已知與未知之間的內在聯系，建立數量之間的相等關系，把日常語言描述抽象成數學表達（數量關系式），再轉換成數學符號（方程式）。因此，教學中不能只強調方程的外在形式，而應設置多元數學情境，經歷多重活動體悟，進行多維模型建構，以凸顯數學知識的本質，促進學生的數學理解。

【教學過程】

一、微課導入，整體感知方程

師：今天，我們要認識一位數學王國中的重量級人物——方程。關于方程，你知道或想知道些什么？（板書：方程）

生：我知道方程是一個算式，方程里有x、y這樣的未知數。

生：我知道方程可以解決很多問題。

生：我想知道方程是誰發明的？

生：我想知道什么是方程？

……

師：其實，方程在我國很早就有了，最初的方程和現在可不一樣。請同學們一起來了解一下方程的發展歷史。（內容略）

師：看了這段視頻，說說你對方程有了哪些新的認識？

（學生各抒己見，完善認知結構。教師相機板書：未知數、等式）

【設計意圖：學生總是帶著已有的生活經驗走進課堂的，后續學習內容總是先前學習內容的進一步發展和提升。課始，開門見山點出要學習的內容，并以開放的姿態引導學生參與知識的建構與生成。之后微課中方程的發展史也是人類社會文明的發展史，學生在觀賞視頻的過程中接納與分析信息，整體感知方程概念。】

二、多元情境，自主建構方程

1.在等量關系中建立方程的概念。

師：看！老師要給大家介紹一個很重要的朋友。（出示天平圖）這個，你們認識嗎？

生：認識！這是天平。

師：那你能用一個數學式子表達此時此刻天平中包含的數量關系嗎？請寫下來。（出示圖1）

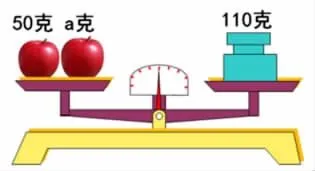
圖1

生：50+a=110。（板書）

師：請問等號從哪里來？你怎么知道是相等的？

生：天平兩邊平衡，表示左右兩邊相等。

師：所以我們可以用等號相連，真不錯！那么請問天平左邊是蘋果，右邊是砝碼，怎么會相等呢？難道蘋果等于砝碼？

生：不是蘋果等于砝碼，而是蘋果的質量等于砝碼的質量。

師：你們明白他的意思嗎？

生：明白，蘋果和砝碼是兩種不同的東西，但它們的數量相等。

師：也就是說，天平左右兩邊的兩種事物的數量相等，我們就可以用這樣的等式來表示，是嗎？（板書：兩種事物，數量相等）

生：是的。

師：那如果沒有天平，你還能用這樣的式子表示圖中的等量關系嗎？（出示圖2、圖3）

圖2

圖3

生：圖2為3x=2.4，圖3為x+2.7=6.9。（板書）

師：你是怎樣找到圖中的等量關系的？

生：圖2中，可以根據數量關系“單價×數量=總價”，找到它們之間的等量關系。每本練習本x元，有3本，一共是2.4元，所以3x=2.4。

師：根據數量關系式來找不同事物間的等量關系是個不錯的方法。那圖3也有這樣的關系嗎？

生：圖3中，x和2.7都是全長的一部分，數量關系是“部分數+部分數=總數”。

師：非常棒！我們一起看，像50+a=100，3x=2.4，x+2.7=6.9 這樣的式子就是方程。現在，你能說一說什么是方程了嗎？

生：方程表示兩種事物之間的數量相等。

生：我覺得方程是未知數和已知數之間的等量關系式。

生：含有未知數的等式，叫做方程。

師：大家說的都很有道理！說明你們對方程有了更深入的理解。

（教師強化板書，形成下圖）

【設計意圖：方程的本質是描述現實世界中的等量關系，它的核心在于用數學的形式表達現實世界中的等量關系。“如果沒有天平，你還能用這樣的式子表示圖中的等量關系嗎？”引導學生脫離天平情境尋找“心中的天平”，進一步豐富對現實問題中未知數和已知數之間的等量關系的認識，體悟方程的概念。】

2.在辨析關系中豐富對方程的理解。

師：我們說，含有未知數的等式叫做方程。請判斷：方程一定是等式，對嗎？

生：正確！方程是含有未知數的等式，所以，方程一定是等式。

師：那等式一定是方程嗎？

生：等式不一定是方程，比如2+8=10是等式，但沒有未知數，就不是方程。

師：你能用集合圈表示出方程和等式之間的關系嗎？

學生展示匯報：

生：方程一定是等式，等式不一定是方程。

師：根據這個集合圈，等式和方程的關系還可以怎么說？

生：等式包含方程，方程是一種特殊的等式。

【設計意圖：于意義建構基礎上辨析方程與等式之間的關系，意在幫助學生進一步豐富對概念的理解，厘清概念的外延。】

3.在關聯情境中溝通方程的認知。

師：下列式子中的一個數、一個字母或一個符號被蓋住了，想一想，這個式子有可能是方程嗎？

出示：

x+★，25-x★16，★×7=42。

生：第一個式子不可能是方程。第二個式子，如果蓋住的是等號，就是方程。第三個式子，如果蓋住的是字母，那就是方程。

師：如果把“★×7=42”中的“★”改成“（）”，還是方程嗎？

生：我認為不是，因為蓋住的不是字母。

生：我覺得是方程，因為括號表示的是未知數。

師：是啊，含有未知數的等式就是方程。那如果把“★”改成“？”還是方程嗎？

生：（異口同聲）是。

師：原來，方程一直隱藏在我們身邊。方程和我們早已經是老朋友了。

【設計意圖：“這個式子有可能是方程嗎？”呈現以往學習中接觸過的含有未知數的等式，在學生破解懸念的興奮中進行知識關聯，再次凸顯方程的本質，有利于學生更加清晰、全面地認識方程。】

三、綜合應用，深入理解方程

1.根據圖中的數量關系列出方程。

生：x-45=128。

師：你是依據怎樣的等量關系列出這個方程的？

生：我的依據是：原價-優惠的價錢=現價。

生：還可以列出方程x-128=45，依據是：原價-現價=優惠的價錢。

生：還有一個方程45+128=x，依據是：現價+優惠的價錢=原價。

師：列方程時，我們一般順向思考找出題中的等量關系，無需逆向思考。一起來看這位同學列的式子45+128=x，你們有什么想說的？

生：他這樣列方程是逆向思考問題。

生：這個方程中45+128的計算結果就是x，感覺與以前學的算術方法一樣。

師：是的。像這樣的等式，x沒有參與運算，本質上還是算術思維，所以列這樣的方程也就沒有意義了。

【設計意圖：方程的價值在于求解，引入方程后，原本需要逆向思考的問題，可以通過順向思考建立等量關系。當學生列出“45+128=x”時，教師并沒有把問題留待日后解決，而是從一開始就讓學生明白，未知數沒有參與運算，本質上還是算術思維，列這樣的方程是沒有意義的。】

2.列方程表示下面各題的數量關系。

（1）

（2）烏龜每分鐘爬行x米，4分鐘共爬行80米。

（3）弟弟收藏郵票x張，姐姐收藏的郵票是弟弟的4倍，姐姐收藏郵票80張。

（4）一種糖果每千克x元，買4千克糖果需要80元。

師：觀察這四道題，你有什么發現？

生：題目不一樣，但列出的方程都是4x=80。

師：四道題目各不相同，為什么列出的方程卻相同？

生：因為它們的數量關系相同，都可以用“每份數×份數=總數”來表示。

師：同一個方程4x=80，等量關系都是“每份數×份數=總數”，它們所表示的具體意義相同嗎？

生：具體現實意義不同。第一題表示“成人人數+兒童人數=總人數”，第二題表示“速度×時間=路程”，第三題表示“弟弟的郵票張數×4倍=姐姐的郵票張數”，第四題表示“單價×數量=總價”。

師：是的，同一個方程可以表示同一類等量關系，但所表示的具體實際意義卻各不相同，這就是方程的魅力所在。想一想，你還能根據方程4x=80編出不同的應用題嗎？

（學生舉例）

【設計意圖：方程是一類事物普遍適用的數學模型。從這一角度來說，同樣的4x=80逆推出的不同問題情境，都表示兩種事物數量相等，而4x=80恰恰是這些不同情境、相似結構的數學問題的統一數學模型。這既豐富了方程的概念，又體會到方程的簡潔美，感悟方程的模型思想。】

四、課堂小結，反思回顧方程

師：通過這節課的學習，你對方程有了哪些認識？有什么收獲與體會？

【教后反思】

關于方程，教材的定義是“含有未知數的等式”，因而，很多教師的理解也往往局限于此。教學時在得出一些等式和不等式的基礎上，通過分類引導學生從中篩選出等式，再篩選出含有未知數的等式，進而揭示方程的意義。筆者認同這一教學線索的合理性，但總覺得沒有將方程本身的意義完全凸顯。在筆者看來，方程的理解不能僅僅停留在“含有未知數的等式”這一層面，要力求達到本質的理解——方程表示的是兩種事物的數量相等，是在未知數和已知數之間建立的等量關系。

對五年級的學生而言，方程不僅是外在形式上的認識，更要讓學生感受它在解決實際問題時建立模型的過程。教學中，借助天平讓學生明白方程所講的是兩種事物的數量相等，進而脫離天平的表象，從現實情境中抽象出等量關系，并用數學式子表示，感受到方程與實際問題的聯系，領會數學建模的思想和基本過程。建構方程概念之后，“價格優惠”問題是讓學生明白根據不同的數量關系式可以找到不同的等量關系，從而列出不同的方程，但未知數沒有參與運算的方程是沒有意義的。緊接著的題組練習是對方程的深入理解，只要等量關系相同，具有相同的數學模型，就可以列出相同的方程，但所表示的具體實際意義各有不同。最后，根據“4x=80”這一方程進行創編，讓學生進一步體會方程的廣泛應用，實現從算術思維向代數思維的過渡，獲得對模型思想的深刻感悟。

其實，無論是方程概念的教學，還是其他數學概念的教學，都應該著眼于學生的多重體悟，重本質而輕形式，重感悟而輕結論，這一直是促進學生深入理解數學概念的有效策略。