尖頭碎片撞擊小尺寸儲罐的模擬實驗*

陳國華,胡 昆,周池樓,祁 帥

(華南理工大學安全科學與工程研究所，廣東 廣州 510641)

容器爆炸碎片引發的多米諾效應事故具有嚴重的破壞性，例如，1984年11月19日，墨西哥城國家石油公司發生的由LPG槽車爆炸引發的連鎖事故，產生了大量的爆炸碎片，造成544人死亡，1 800多人受傷，120萬人緊急疏散。研究容器爆炸產生的爆炸碎片作用下臨近儲罐的結構動態響應特性及其破壞機理，是化工園區安全與石油儲備安全面臨的重要挑戰之一。

目前，國內外學者對多種類型的板/殼結構在不同撞擊荷載下的動力學響應開展了實驗研究。例如，穆建春等[1]研究了自由梁中部在平頭子彈橫向正沖擊下的穿透及變形，估算出局部剪切能、梁彎曲變形能、子彈及梁的殘余動能在子彈初動能中所占的比例；A.Palmer等[2]系統研究了兩端固支薄壁圓管在一般撞擊速度(46～325 m/s)作用下的臨界穿孔動能及管內充裝液體的影響；Y.Wang等[3]分別研究了不同充裝系數、不同壁厚的儲水罐在沖擊荷載下的動力學響應情況；D.Sun等[4]開展了儲罐外復合材料防護層抵抗高速小質量碎片撞擊防護性能的實驗研究，主要考慮的參數有：防護層厚度、面密度、纖維結構、碎片撞擊速度，研究發現在單向纖維(UD)材料中存在臨界厚度，使防護層的能量吸收能力最大，撞擊速度達到彈道極限防護層背面的破孔凸起最嚴重；H.Yu等[5]開展了鐵路危化品槽罐車殼的沖擊實驗，研究其動力學響應，結果發現刺穿能量隨著初始液體壓力的降低而升高，隨著槽罐壁厚的增大而增大，隨著撞擊物接觸面積的增大而增大；唐恩凌等[6]開展了球型彈丸正撞擊圓柱殼自由梁實驗，研究了彈丸速度、殼體直徑與壁厚對穿孔直徑的影響。但是這些實驗設置多數采用撞擊物正撞擊目標板/殼，較少涉及到撞擊物以不同角度撞擊(即斜撞擊)下板/殼結構的失效模式與規律的實驗研究。

本文中通過開展0°、15°、30°以及45°軸向撞擊角的碎片撞擊不同壁厚小尺寸儲罐的模擬實驗，得到不同壁厚的罐壁在不同軸向撞擊角碎片撞擊下的變形破壞情況及碎片剩余速度。同時，基于穿甲力學理論和動量守恒定理，推導出適用于0°～45°軸向撞擊角的尖頭碎片剩余速度理論計算公式，并通過實驗數據驗證公式的準確性。研究結果可用于殼體結構在尖頭碎片軸向撞擊下的破壞預測，為殼體結構的安全防護設計提供理論參考。

1 碎片撞擊小尺寸儲罐模擬實驗方案

使用某型號步槍作為實驗發射裝置，以尖頭彈作為尖頭碎片，開展尖頭碎片撞擊小尺寸儲罐模擬實驗。其中碎片質量8.8 g，直徑7.82 mm。實驗示意圖與尖頭碎片結構示意圖分別如圖1～2所示。

由于爆炸碎片撞擊儲罐主要造成前壁破壞，因此主要研究碎片作用下儲罐前壁的破壞情況。實驗試件采用?300 mm×300 mm半結構柱殼模擬的小尺寸儲罐，罐壁壁厚h=1.00，1.50，2.00，2.75 mm，采用化工儲罐設備常用材料Q235。實驗過程中尖頭碎片軸向撞擊角θ=0°，15°，30°，45°。小尺寸儲罐兩側各放置一臺Model 57型紅外光感應式子彈測速儀，分別測量出尖頭碎片撞擊速度vi的實驗值和穿透罐壁后的剩余速度vr的實驗值。實驗共進行了16組，如表1所示。

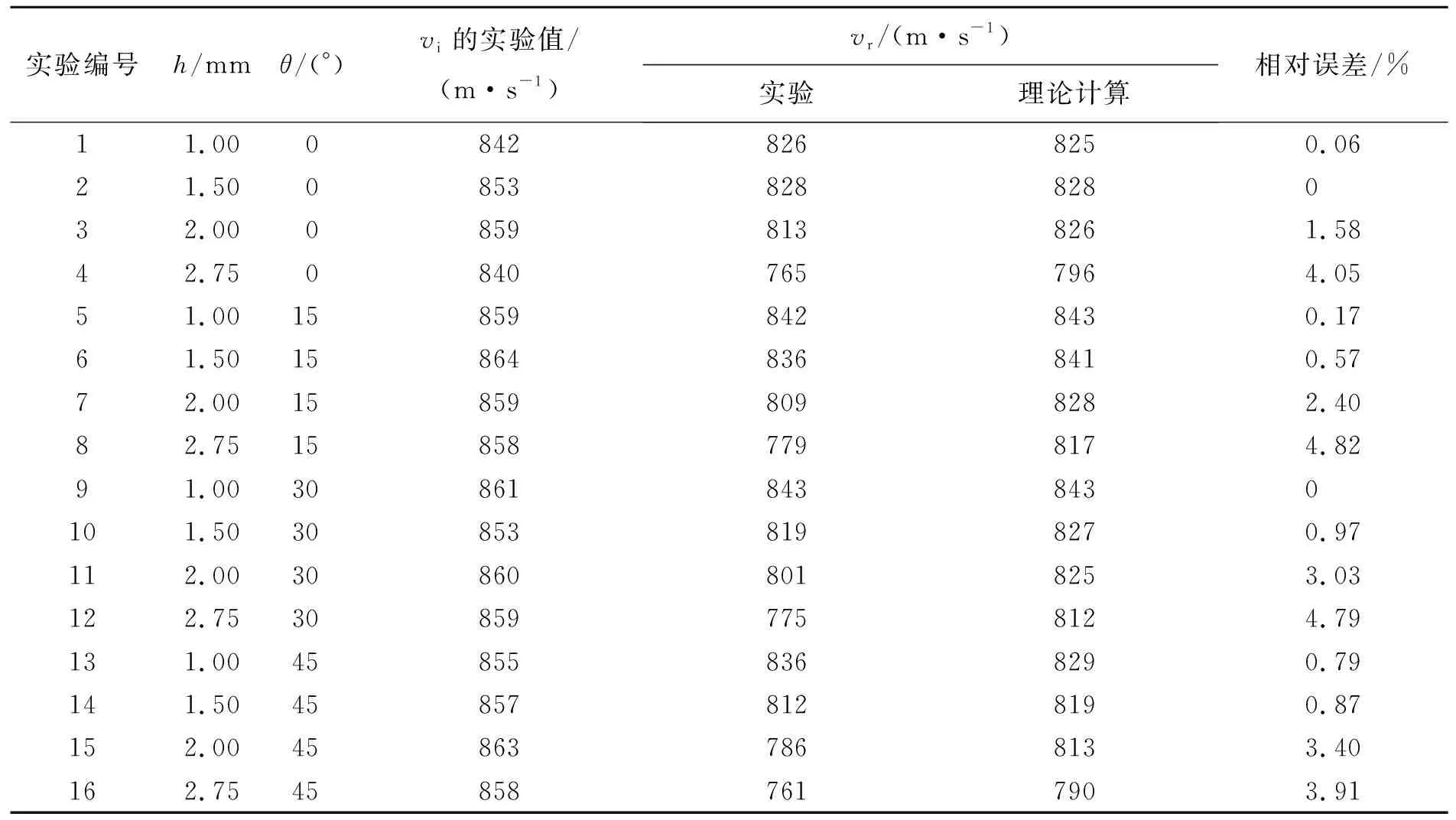
實驗編號h/mmθ/(°)vi的實驗值/(m·s-1)vr/(m·s-1)實驗理論計算相對誤差/%11.0008428268250.0621.500853828828032.0008598138261.5842.7508407657964.0551.00158598428430.1761.50158648368410.5772.00158598098282.4082.75158587798174.8291.00308618438430101.50308538198270.97112.00308608018253.03122.75308597758124.79131.00458558368290.79141.50458578128190.87152.00458637868133.40162.75458587617903.91

注：相對誤差為尖頭碎片剩余速度的實驗值與理論計算值之間的相對誤差。

2 實驗結果分析

2.1 穿透形貌

圖3為0°軸向撞擊角的尖頭碎片穿透壁厚1.0 mm儲罐的正面、背面形貌圖。由圖3可見，尖頭碎片穿透罐壁后穿孔正面形成近似圓形的穿孔，邊緣整齊，罐壁失效區域局部變形很小，罐壁整體幾乎沒有變形。穿孔背面呈現花瓣型開裂，花瓣彎曲角度接近90°，從花瓣根部到頂部厚度逐漸變薄。當碎片侵入罐壁材料后，推動罐壁材料向前運動產生彎矩，在罐壁的軸向、徑向、環向三個方向形成高的拉應力。當達到罐壁材料的拉伸強度極限時，就會在碎片撞擊點四周的不同方向上產生裂紋，伴隨著較小的結構變形，罐壁穿孔呈現花瓣型開裂。由于碎片在侵徹過程中推動罐壁材料形成的拉應力，導致從花瓣根部到頂部厚度逐漸變薄。

圖4為30°軸向撞擊角的尖頭碎片穿透壁厚2.0 mm儲罐的正面、背面形貌圖。15°、30°以及45°軸向撞擊角的尖頭碎片穿透罐壁具有類似的形貌特征，穿孔正面都形成近似橢圓形的穿孔，且穿孔軸向直徑da大于穿孔環向直徑dr。罐壁整體幾乎沒有變形，罐壁失效區域局部變形很小，但大于0°軸向撞擊角的罐壁失效區域變形，穿孔附近邊緣有明顯的凹陷變形，并產生2個條形翻邊。穿孔背面呈現花瓣型開裂，沿碎片飛行方向形成較大的花瓣，而穿孔上部罐壁材料沒有外翻形成花瓣。原因是：(1)在尖頭碎片沿著罐壁軸向方向的速度分量作用下，碎片與罐壁之間產生高的剪應力，擠壓穿孔上部的罐壁材料形成條形翻邊；(2)在尖頭碎片沿著罐壁徑向方向的速度分量作用下，碎片推動穿孔下部的罐壁材料形成高的拉應力，下部的罐壁材料在穿孔背面形成花瓣形開裂。

2.2 穿透能量

穿透能量是指尖頭碎片以一定角度穿透小尺寸罐壁所消耗的能量。由文獻[5]可知,尖頭碎片撞擊罐壁的穿透能量Ep近似計算方法為：

(1)

式中:m為尖頭碎片質量。

由圖5(a)可知，當尖頭碎片撞擊角一定時，壁厚越大，穿透罐壁所需的穿透能量越大。對穿透能量隨壁厚變化的曲線進行參數擬合，如圖5(b)所示，以獲得罐壁穿透能量公式。文獻[7]中的研究表明,穿透能量與壁厚存在二次函數關系，選用二次多項式對實驗結果進行擬合，其函數表達式為：

Ep=a+bh+ch2

(2)

為了得到含撞擊角的罐壁穿透能量與壁厚之間的函數表達式，參數a、b、c采用多項式函數擬合為軸向撞擊角的關系式，擬合結果如下：

a=-22.24+4.07θ-0.34θ2

(3)

b=98.13-4.44θ+0.44θ2

(4)

c=45.02+1.23θ-0.11θ2

(5)

將擬合的式(3)～(5)代入式(2)，即可得到0°～45°軸向撞擊角的小質量尖頭碎片高速穿透材料為Q235的罐壁穿透能量與壁厚、軸向撞擊角之間的關系式：

Ep=(-0.11θ2+1.23θ+45.02)h2+(0.44θ2-4.44θ+98.13)h+

(-0.34θ2+4.07θ-22.24)

(6)

圖6為軸向撞擊角與穿透能量關系圖，由圖6可知：

(1)當壁厚一定時，尖頭碎片軸向撞擊角越大，穿透罐壁所需的穿透能量越大。原因是軸向撞擊角越大，碎片沿罐壁軸向方向的速度分量越大，導致碎片沿軸向撞擊罐壁的滑擦距離增大，因此穿透罐壁所需要的穿透能量也就越大。且在壁厚一定時，曲線斜率隨軸向撞擊角的增大而增大，表明軸向撞擊角越大，對罐壁的穿透能量影響越顯著;

(2)隨著壁厚增大，曲線的整體斜率也隨之增大，說明壁厚越大，罐壁的穿透能量對軸向撞擊角越敏感。

2.3 穿孔直徑

穿孔直徑指尖頭碎片穿透罐壁后，在罐壁上形成孔洞的直徑，包括穿孔軸向直徑da和穿孔環向直徑dr，如圖4(a)所示。0°軸向撞擊角的尖頭碎片撞擊罐壁形成的穿孔形狀并不是圓形，而是軸向直徑略大于環向直徑的橢圓。原因是儲罐罐壁的軸向強度極限小于環向強度極限，在校核圓筒或柱殼等結構的應力時，軸向應力不大于許用應力，而環向應力不大于1.25倍的許用應力。因此在碎片侵徹過程中，儲罐罐壁在軸向比環向更容易發生破壞，導致形成的穿孔軸向直徑略大于環向直徑。

圖7為穿孔直徑與壁厚、軸向撞擊角關系圖，由圖7可知：

(1)從圖7(a)可以看出，當軸向撞擊角一定時，0°軸向撞擊角的尖頭碎片穿透罐壁的穿孔軸向直徑隨著壁厚的增大而減小。原因是碎片在侵徹擴孔過程中會擠壓罐壁材料，在孔邊緣形成一圈整齊的翻邊，且壁厚越大，侵徹擴孔越難，所形成的翻邊厚度越大，導致軸向直徑減小。當軸向撞擊角一定時，15°、30°以及45°軸向撞擊角的尖頭碎片穿透罐壁的穿孔軸向直徑隨著壁厚的增大而增大。當軸向撞擊角從15°增大到45°時，曲線斜率逐漸增大，即軸向撞擊角越大，穿孔軸向直徑對壁厚越敏感。

(2)從圖7(b)可以看出，當壁厚一定時，碎片軸向撞擊角越大，穿孔軸向直徑越大。且曲線曲率隨著軸向撞擊角的增大而增大，說明軸向撞擊角對穿孔軸向直徑的影響更大。原因是軸向撞擊角越大，碎片沿著罐壁軸向方向的速度分量越大，碎片沿軸向撞擊罐壁的滑擦距離越大，導致穿孔軸向直徑增大。但當軸向撞擊角增大到一定值時，尖頭碎片因接觸罐壁后發生滑動而不能穿透罐壁。

(3)從圖7(c)～(d)可以看出，隨著碎片軸向撞擊角以及壁厚的變化，穿孔環向直徑變化幅度不大，最大穿孔環向直徑比最小的僅高出0.53 mm。圖7(c)中，因翻邊的影響，0°軸向撞擊角尖頭碎片對罐壁造成的穿孔環向直徑隨著壁厚的增大而減小。15°、30°以及45°軸向撞擊角尖頭碎片對罐壁造成的穿孔環向直徑隨著壁厚的增大而增大，曲線曲率隨著壁厚的增加而減小。

(4)從圖7(d)可以看出，1.00 mm壁厚的穿孔環向直徑隨著尖頭碎片軸向撞擊角的增大先減小后增大。1.50、2.00 、2.75 mm壁厚的穿孔環向直徑均隨著碎片軸向撞擊角的增大而小幅度增大。

3 碎片穿透罐壁的剩余速度計算

3.1 0°軸向撞擊角

因罐壁曲率對儲罐吸收能量影響不大[8]，且相對于小尺寸儲罐，尖頭碎片產生的穿孔局部變形很小，將花瓣型開裂穿孔附近的罐壁近似視為平面板[9]，推導尖頭碎片穿透罐壁后的剩余速度vr的理論計算公式。圖8為尖頭碎片以0°軸向撞擊角穿透罐壁示意圖。

(1)穿透過程動量守恒定理

設r為尖頭碎片穿過罐壁x′處的穿孔半徑，m為尖頭碎片質量，v為尖頭碎片穿過罐壁x′處的速度，vi為尖頭碎片開始穿透罐壁時的撞擊速度。由文獻[10]，根據動量守恒定理得：

mvi=mv+Mw(x′)

(7)

式中:Mw(x′)為碎片穿過罐壁x′處罐壁開裂部分的動量。

(2)穿透過程開裂部分有效質量

儲罐壁厚為h，密度為ρ，原來距離尖頭碎片軸線為s的圓環，變形后沿著x方向位移為λ，該圓環的動量以及距尖頭碎片軸線為s的圓環微元的速度分別為：

(8)

(9)

則碎片穿過罐壁x′處罐壁開裂部分的動量為：

(10)

穿透過程中罐壁開裂部分的有效質量為：

(11)

(3)穿透罐壁的剩余速度

設β為尖頭碎片錐角的一半，花瓣在變形過程中未發生伸長，所以穿透前距離花瓣尖端為s的微元，形成花瓣后仍為s(見圖8)，因此得出：

λ=(x′tanβ-s)cosβ

(12)

尖頭碎片錐形部分穿過罐壁即表示已經完全穿透，此時r=R，結合式(7)、(11)～(12)得到尖頭碎片穿透罐壁后的剩余速度vr的計算公式：

(13)

3.2 非0°軸向撞擊角

(1)穿透過程開裂部分有效質量

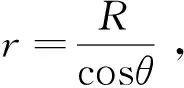
(14)

將式(9)代入式(14)中并積分，得到碎片穿過罐壁后x′處罐壁開裂部分的動量：

(15)

此時，穿透過程中罐壁開裂部分的有效質量為：

(16)

(2)穿透罐壁的剩余速度

設β為尖頭碎片錐角的一半，γ=90°-θ-β，花瓣在變形過程中未發生伸長，所以穿透前距離花瓣的尖端為s的點，形成花瓣后仍為s，通過幾何關系分析，得出位移λ為：

(17)

尖頭碎片穿過罐壁后x′處，距尖頭碎片軸線為s的圓環微元的速度為：

(18)

引入參數G，因θ和β是確定的，故G確定：

(19)

結合式(7)、(16)和(19)，得到尖頭碎片以非0°軸向撞擊角穿透罐壁后的剩余速度vr的計算公式：

(20)

3.3 結果驗證

將尖頭碎片穿透罐壁的剩余速度理論計算值與實驗值進行對比驗證，對比結果如表1所示。尖頭碎片剩余速度理論計算值與實驗值十分接近，最大相對誤差為4.79%，最小相對誤差為0，平均相對誤差為1.97%，驗證了剩余速度理論計算公式的準確性，可適用于0°～45°軸向撞擊角的尖頭碎片穿透罐壁的剩余速度預測。

當軸向撞擊角一定時，壁厚越大，碎片剩余速度的相對誤差越大，原因是壁厚越大，碎片與罐壁之間接觸面積越大，摩擦耗能越大，且穿孔附近的局部變形耗能越大，導致相對誤差越大。當壁厚一定時，軸向撞擊角越大，相對誤差也越大，原因是軸向撞擊角越大，尖頭碎片沿著罐壁軸向方向的速度分量越大，碎片與正面罐壁材料之間的滑擦變形耗能越大，同時摩擦耗能越大，穿孔附近的局部變形耗能越大，導致相對誤差越大。

4 結 論

通過開展尖頭碎片撞擊小尺寸儲罐模擬實驗，得出以下結論：

(1)0°軸向撞擊角的尖頭碎片穿透罐壁，穿孔正面形成近似圓形的穿孔，穿孔背面呈現花瓣型開裂，彎曲角度接近90°，從花瓣根部到頂部罐壁材料逐漸變薄； 15°、30°以及45°軸向撞擊角的尖頭碎片穿透罐壁后穿孔正面形成近似橢圓形的穿孔以及2個條形翻邊，且穿孔軸向直徑da大于穿孔環向直徑dr，穿孔背面呈現花瓣型開裂，沿碎片飛行方向形成較大的花瓣。

(2)當尖頭碎片撞擊角一定時，壁厚越大，所需的穿透能量越大。當壁厚一定時，尖頭碎片軸向撞擊角越大，所需的穿透能量也越大，軸向撞擊角對穿透能量影響越顯著。且壁厚越大，穿透能量對軸向撞擊角越敏感。

(3)軸向撞擊角與壁厚對穿孔軸向直徑影響顯著。15°、30°及45°軸向撞擊角的尖頭碎片穿透罐壁的穿孔軸向直徑隨著壁厚的增大而增大，且軸向撞擊角越大，穿孔軸向直徑對壁厚越敏感；當壁厚一定時，碎片軸向撞擊角越大，穿孔軸向直徑也越大，且軸向撞擊角對穿孔軸向直徑的影響越顯著。但隨著碎片軸向撞擊角以及壁厚的變化，穿孔環向直徑變化幅度不大。

(4)推導出適用于0°～45°軸向撞擊角的尖頭碎片穿透罐壁的剩余速度理論計算公式，且通過實驗結果驗證了公式的準確性。