混凝土爆破損傷的SPH-FEM耦合法數值模擬*

王志亮,畢程程,李鴻儒

(合肥工業大學土木與水利工程學院，安徽 合肥 230009)

爆炸過程涉及炸藥爆炸能量的高速釋放、沖擊波在介質中的快速傳播、混凝土的損傷破裂乃至飛濺等方面的問題，目前的理論研究水平在準確描述爆炸過程方面尚存在不足。實驗研究由于成本高、實施周期長以及很難全面地測定相關參量，最終往往只能得到混凝土在爆炸破壞作用下的終態響應結果以及獲取部分監測點的時程信息,而數值模擬可以很好地再現爆炸響應的中間過程，并且能有效地描述混凝土在爆炸作用下的真實動態響應情況。相比于傳統的FEM數值算法，如Lagrange、Euler以及ALE算法，光滑粒子流體動力學(smoothed particle hydrodynamics, SPH)方法[1]集合了無網格法、拉格朗日法和粒子流法的優勢，能夠避免Lagrange算法中的網格畸變問題、Euler算法中的重分和輸運計算問題以及ALE算法兼具雙重網格屬性帶來的計算耗時較長等問題。SPH法所具有的無網格屬性可以避免網格扭曲變形造成的精度損失，拉格朗日屬性可以得到較為準確的模擬結果，粒子屬性能夠較好地展現爆炸沖擊所產生的成坑、物質飛濺等破壞現象。但是由于算法差異，SPH法相對于傳統的FEM數值算法計算效率較低，且在邊界處理上也存在著一定的問題。

針對SPH法存在的問題，諸多學者提出了SPH-FEM耦合法，即建模時將爆炸近區大變形區域采用SPH建模，而在爆炸遠區的小變形區域采用FEM建模。這樣既能避免大變形區域內的網格畸變，又可以減少SPH的計算域，從而大大提高計算效率。胡英國等[2]采用SPH-FEM耦合法對深孔梯段爆破的動力效應進行了數值模擬，模型在爆破近區采用SPH粒子，遠區采用有限單元，得出該耦合算法能夠較為準確地模擬爆破近區的巖體運動和損傷特征；王維國等[3]模擬了炸藥在砂土地基中的觸地爆炸，分別比較了純SPH模型和SPH-FEM耦合模型對計算結果的影響，得出純SPH模型計算耗費的時間約是SPH-FEM耦合模型的3倍，而計算精度基本保持一致，模擬得到的爆炸成坑效果與經驗值相一致；崔溦等[4]采用SPH-FEM耦合數值法，研究了土中鋼筋混凝土箱涵的爆炸動力響應問題，其將SPH法用于模擬爆破近域土體，而FEM法用于模擬遠場土體和鋼筋混凝土箱涵；Lu等[5]研究地下結構在淺埋炸藥爆炸作用下的動態響應時，分別針對二維和三維的SPH-FEM模型進行數值比較，得出二維模型計算的結果更為精確且波形穩定；Koneshwaran等[6]在分析地表炸藥爆炸對地下隧道的破壞效應時，對炸藥及其附近的土體采用SPH粒子，并討論了常見的幾種SPH-FEM耦合方法；VUYST等[7]結合平板對撞的例子，討論了SPH法、FEM法以及SPH-FEM耦合算法在計算效率和精度上的差異，得出SPH-FEM耦合算法效果最佳，并在剛形體跌落入水以及子彈擊穿靶板例子上得到良好驗證；楊剛等[8]模擬炸藥在混凝中爆炸時，分別采用純Euler算法、純SPH算法、Euler-Lagrange耦合算法以及SPH-Lagrange耦合算法，指出用純Euler算法或純SPH算法描述混凝土時，計算得到的壓力時程曲線在衰減段會有較大的數值波動。相比較而言，Euler-Lagrange耦合算法以及SPH-Lagrange耦合算法模擬效果較好。

Holmquist-Johnson-Cook(HJC)本構模型[9]是針對混凝土材料提出的一種率相關的損傷本構模型，能有效地計算混凝土在高應變率下的大變形問題。由于該模型能夠較好地描述混凝土在高速碰撞、侵徹以及爆炸作用下的力學行為，適用于拉格朗日和歐拉算法，現已被LS-DYNA程序引入,并被廣泛運用[10-15]，紀沖等[16]、梁超[17]還將SPH-FEM耦合法結合HJC本構模型運用到彈體侵徹混凝土上，而目前基于SPH-FEM耦合法模擬混凝土爆破的公開發表的成果很少，結合爆破問題對HJC本構中各參數敏感度進行分析的研究更少。本文中針對C30混凝土中的爆破成坑等問題，開展較深入的研究，力圖得出一些具有參考價值的結論。

1 算 法

1.1 SPH基本原理

SPH方程可表述[1]如下。

第一步：使用積分表達式對函數進行近似，任一函數f(x)的積分近似表達式為：

(1)

式中：積分域為整個問題域空間,W(x-x′,h)為光滑核函數,h為光滑長度。

第二步：粒子近似法，即用粒子函數對式(1)的積分表達式離散化，通過對離散化的粒子插值得到函數值，也就是使用光滑核函數W影響范圍內的臨近粒子j的運動信息求和平均代替參考粒子i的運動狀態，則粒子i處的函數近似式為：

(2)

式中:mj、ρj分別為粒子j的質量和密度(j=1, 2, …,N),N為在粒子i的支持域內粒子數的總量。

對粒子i的求解可通過使用光滑核函數W支持域內的粒子j求和得到(見圖1)。圖中h為光滑長度，W為光滑核函數，κ是與x處光滑函數相關的常數，Ω表示支持域，S為粒子作用邊界。

1.2 SPH-FEM耦合方式

SPH-FEM耦合法的關鍵是在最靠近有限元網格的一排 SPH 粒子如何順利地將各物理力學信息傳遞給有限單元。目前比較常見的有三種方法[6]：第一種是將靠近SPH 粒子的有限單元上的節點賦予粒子屬性，SPH 粒子將各信息傳遞給有限單元上的節點，再通過節點傳遞給單元；第二種是在SPH粒子與有限單元之間建立混合區，該區域粒子與單元相互重合，將粒子攜帶的信息過渡到單元上；第三種是通過定義節點與面之間的接觸來傳遞信息(見圖2)，常見的包括滑動接觸和固連接觸[3]。

本文中采用固連接觸的方式將SPH粒子與有限單元聯系起來，最靠近有限元網格的SPH粒子將從其他粒子傳遞過來的能量、動量以及運動方程等物理力學信息傳遞給有限單元，同時以點-面固結的方式保證兩者間位移與變形的協調。接觸通過在LS-DYNA中建立模型后生成的k文件中添加關鍵字 CONTACT_TIED_NODES_TO_SURFACE來定義[18]，并通過關鍵字CONTROL_CONTACT調節接觸剛度等參量。

2 本構模型

2.1 混凝土材料模型

HJC損傷本構模型考慮了高靜水壓力、高應變率和材料的損傷效應，主要包括三個部分：強度模型、狀態方程和損傷模型[9,18]。

強度模型是以特征化等效應力進行描述，可表示為：

(3)

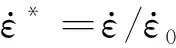
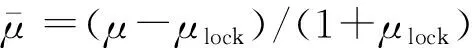
損傷模型如圖4所示，由等效塑性應變和體積應變累積而成，其演化方程為：

(4)

D1(P*+T*)D2≥EFmin

(5)

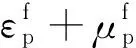
本文中涉及到的C30混凝土[19-20]基本力學參數為：密度ρ0=2 400 kg/m3，抗壓強度fc=39.2 MPa，抗拉強度T=3.162 MPa，彈性模量E=33.4 GPa，泊松比ν=0.202。混凝土剪切模量G和體積模量K根據下式確定：

G=E/[2(1+ν)]

(6)

K=E/[3(1-2ν)]

(7)

求得G=13.89 GPa，K=18.68 GPa。

混凝土達到彈性極限時的靜水壓力Pcrush和體積應變μcrush可由下式確定：

Pcrush=fc/3

(8)

μcrush=Pcrush/K

(9)

求得Pcrush=13.07 MPa，μcrush=0.000 7。

損傷參數D1可按照公式D1=0.01/(1/6+T*)確定，其中T*=T/fc，求得D1=0.04。參數D2和Smax對模擬結果的影響很小[10,14]，因此D2按文獻[9]取為1，Smax取為7。

文獻[19]針對C30混凝土在考慮率型微損傷演化的條件下改進了Johnson-Cook模型，并基于相關實驗給出了極限面參數A、B、N及應變率影響參數C的值，所提出的模型在混凝土動態實驗中得到了良好的應用。本文中基本力學參數大多取自文獻[19]，考慮到HJC各參數之間耦合緊密，故參數A、B、N和C仍取自文獻[19]。狀態方程參數Plock、μlock、K1、K2和K3在缺乏實驗數據的情況下，大多取自文獻[9]。根據文獻[11]對FS的假設，認為混凝土達到極限密度ρmax時，體積應變達到最大值μmax，即：

(10)

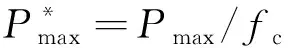
表1 C30混凝土HJC參數Table 1 HJC parameters of C30 concrete

2.2 炸藥材料模型

炸藥按均勻連續介質考慮，采用MAT_HIGH_EXPLOSIVE_BURN材料模型和JWL狀態方程精確描述爆炸過程中爆炸產物的體積、壓力以及能量特性，表達式為[18]：

(11)

式中：P為爆轟壓力，V為相對體積，E0表示初始體積內能，A、B、R1、R2和ω為炸藥常數。

炸藥各參數取值分別為[21]：ρ=1 630 kg/m3，Dv=6 930 m/s，Pcj=27.0 GPa，A=374 GPa，B=7.33 GPa，R1=4.15，R2=0.95，ω=0.3，E0=7.0 GJ/m3，V0=1.0。

2.3 土體材料模型

土體采用MAT_SOIL_AND_FOAM材料模型，其理想塑性屈服函數為[18]：

φ=J2-(a0+a1σ+a2σ2)

(12)

式中：J2=σijσij/2，σij為偏應力分量；σ為平均應力；常數α0、α1和α2為無量綱曲線J2-σ二次擬合曲線常數項。

土體主要計算參數為[22]：密度為1.80 g/cm3，剪切模量為16.01 MPa，體積卸載模量為1.26 GPa，剪切屈服面參數α0=2.4×106Pa2，α1=1.360×104Pa和α2=0.123 2。

3 模擬分析

3.1 模型建立

穆朝民等[20]、李重情等[23]為研究變埋深條件下混凝土中爆炸壓力和加速度的傳播規律，進行了多組實驗。實驗設計在室外空曠地區，在地上開挖一個邊長為3 m的立方體爆坑，沿深度方向布設6個測點，用于安裝壓力傳感器和加速度傳感器，然后現場澆筑混凝土直至填滿實驗坑，并在澆筑時預留裝藥孔，填裝1 kg TNT，最后進行爆炸實驗。本文以此實驗為基礎，對其進行數值模擬。文獻[20,23]給出了炸藥在不同埋深條件下包括裝藥比例距離為-0.25 m/kg1/3的空爆(炸藥懸置空中距混凝土表面0.25 m)、-0.053 m/kg1/3的觸地爆(炸藥置于混凝土表面)、0 m/kg1/3的半埋爆(炸藥半埋于混凝土中，且炸藥中心處于混凝土頂面中心處)以及0.8 m/kg1/3的全埋爆(炸藥全部埋于混凝土內且距混凝土表面0.8 m)等爆炸實驗結果，而其中只給出了裝藥比例埋深為0和0.8 m/kg1/3時相應的壓力和加速度時程數據。因此，為方便將模擬結果與實驗結果進行對比，同時更好地展現爆炸破壞的效果，本文中選擇模擬裝藥比例埋深為0 m/kg1/3的半埋爆情況。

物理模型如圖5所示，立方體混凝土邊長為300 cm，炸藥選用1 kg TNT，按照等體積原則將炸藥簡化成尺寸為8.5 cm×8.5 cm×8.5 cm的立方體。混凝土的四周及底部與土體接觸，土體厚度均取10 cm。測點1～6距炸藥中心的距離依次為25.5、51.5、81.0、125.6、187.9和250.4 cm。

計算模型如圖6所示，由于模型具有對稱性，為節省計算時間只建了1/4模型。考慮到混凝土采用的是HJC本構模型，該模型無法模擬混凝土在爆炸荷載作用下的裂紋擴展、破碎等過程，因此通常情況下需要添加單元失效準則MAT_ADD_EROSION，使處于破壞區的單元失效以形成破壞效果。然而，單元失效準則對粒子并不起作用，粒子只會產生運動而不會憑空消失，此時如果混凝土粒子區域選擇得過小，爆炸荷載傳遞到混凝土近區的有限單元上導致該處的單元刪除，則粒子與單元之間的接觸算法會失效，影響壓力波的傳播和單元與粒子之間位移變形的協調性。如果不添加單元失效準則，爆炸近區混凝土有限單元會發生變形，形成“杯口狀”的凸起，跟實際的爆破形態并不一致；若將粒子區域取得過大，這樣不僅會造成計算時間的增加，對應的存儲空間也會急劇增加，一般的計算機很難滿足要求。經過多次嘗試，最終將該部分混凝土(近區)的尺寸設定為30 cm×30 cm×30 cm。由于粒子能夠很好地展現混凝土破碎與拋擲等過程，因此本模型中無需添加單元失效準則。

模型主要在LS-DYNA軟件中建立，結合關鍵字的添加與修改，大體可分為三步：(1) 在LS-DYNA中建立FEM模型；(2)采用solid center建立SPH模型；(3)在LS-DYNA中求解，用LS-PREPOST處理計算結果，詳見圖7。在邊界處理上，土體外側及底面設定透射邊界，用來模擬該方向的無限區域；土體內側與混凝土相接觸的部分定義面面接觸，并考慮摩擦力的影響；對稱面處設置SPH對稱邊界和FEM對稱邊界，用以約束單元和粒子在對稱面處的法向運動；混凝土(近區)粒子與混凝土(遠區)有限單元之間采用固連接觸的方式定義耦合算法，即通過添加關鍵字 CONTACT_TIED_NODES_TO_SURFACE來定義。

3.2 結果分析

圖8展示了1 kg TNT炸藥半埋爆炸時爆坑的形成過程。在爆炸初期，隨炸藥能量的釋放，由于沖擊波壓力遠大于混凝土的動態抗壓強度，炸藥爆炸產生的高壓氣體迅速破碎了炮孔周圍的混凝土。同時，應力波在混凝土中引起了徑向和環向拉應力，導致大量裂隙出現，并向自由面方向擴展。自由面處的混凝土在反射拉應力作用下被拉裂、發生片落，并在爆生氣體的作用下產生拋擲。隨著爆生氣體膨脹和楔入，徑向和環向裂隙進一步擴大，拋擲現象加劇，爆破漏斗逐步形成。最后，炸藥能量耗散殆盡，其中一部分通過自由面直接擴散到空氣中，另一部分能量則被用于破碎、拋擲混凝土以及形成爆炸震動波，爆破漏斗形態漸趨穩定。

為研究爆炸波在混凝土中的傳播特性，同時與實測數據作對比，采用1 kg TNT炸藥，則測點1～6距炸藥中心的比例距離Z依次為0.255、0.515、0.810、1.256、1.879和2.504 m/kg1/3。考慮到各測點曲線峰值相差較大，圖9～10僅顯示了中間4個測點相關的壓力時程曲線和加速度時程曲線。

由圖9～10可以看出，炸藥起爆后應力波迅速傳播，當達到測點后，壓力和加速度在很短的時間內迅速達到峰值，然后逐漸衰減，最后趨近于零。不同測點處的壓力和加速度有所差異，即隨著測點與藥包比例距離的增加，測點處的峰值壓力和峰值加速度逐漸減小，正壓作用時間有所延長。圖9中各測點的壓力在經歷過正壓段后出現持續時間較長且峰值較小的負壓段，這可能是由于混凝土試樣較小，爆炸波傳播到四周邊界后經多次反射作用造成的[24]；圖10中各測點加速度呈現單峰且峰后出現連續的小幅度數值振蕩，這也與實際結果較為吻合[20]。

表2為不同測點處實測數據[20,23]與計算結果的對比，可以看出計算得到的峰值壓力與對應的實測數據吻合度較高，誤差基本在±12%以內，而峰值加速度相對而言誤差偏大，但大多也都在±20%以內。

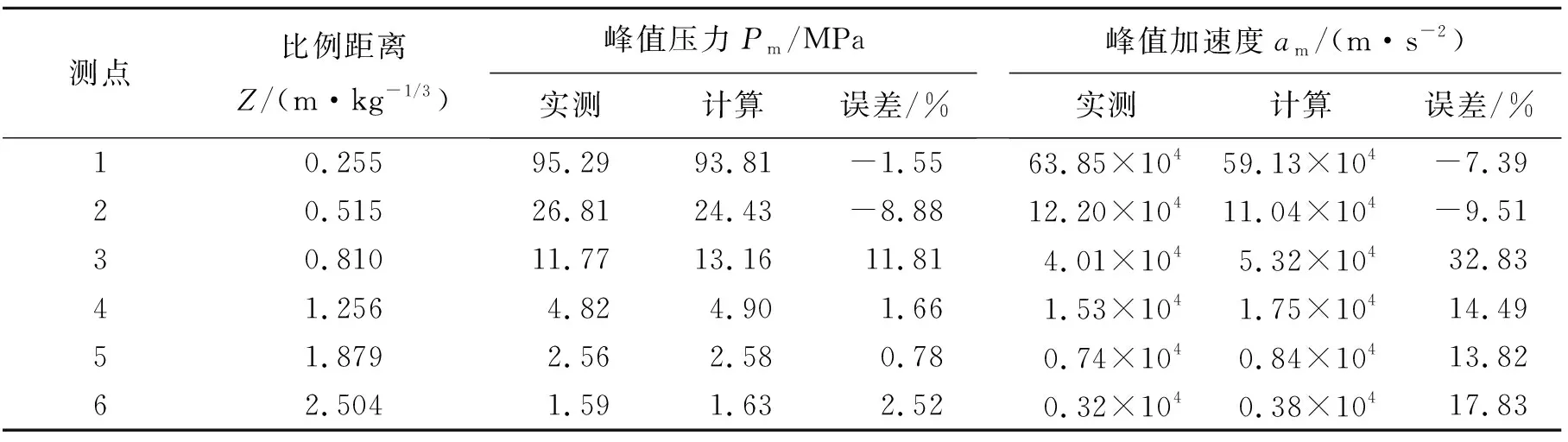
表2 不同測點處計算結果與實測結果對比Table 2 Comparison between calculated results and measured results at different test points

3.3 HJC參數敏感度分析

模型參數的敏感度分析是指研究一個或多個不確定性參數的變化對計算結果產生的影響，即模型對某個參數或某組參數變化反應的敏感程度。通過敏感度分析，既可以識別對模型計算結果起決定性作用的參數，又可較好地評價參數偏差對計算結果產生的影響，這在本構參數確定與反演等方面有著廣泛的應用。

考慮到混凝土采用的HJC本構參數涉及到21個之多，加上狀態方程參數大多沿用文獻[9]，因此想要進一步提高模擬的精度，還需對各參數的敏感度進一步分析。依照每次分析所涉及到的參數個數，可將敏感度分析分為全局敏感度分析和局部敏感度分析，全局敏感度分析需要檢驗多個參數的變化對計算結果總的影響，同時評價每個參數及各參數之間對計算結果的影響；局部敏感度分析只需每次檢驗單個參數對計算結果的影響。考慮到HJC本構模型各參數之間耦合緊密，若采用全局敏感度分析，一方面難以確定參數變化所遵循的標準和范圍，另一方面要考慮到每個參數及各參數之間對計算結果的影響，計算量太大。因此，本文中采用局部敏感度分析法[10,13-14]，即研究HJC模型中單個參數變化對計算結果的影響。

以0.515 m/kg1/3處的測點作為研究對象，采用控制變量法，將21個參數在表1的基礎上分別單獨作±40%和±20%的變化，將每次計算的結果(包括峰值壓力和峰值加速度)與表1中初始參數計算結果的比值作為研究參數敏感度的指標[10,13]。通過大量的數值計算，得到C30混凝土HJC模型不同參數變化率下引起的峰值壓力和峰值加速度的變化率，如圖11～12所示。

可以看出，對峰值壓力(Pm)影響比較大的參數有9個：ρ、fc、A、B、G、Pcrush、μcrush、Plock和μlock；對峰值加速度(am)影響比較大的參數有7個：ρ、fc、A、B、μcrush、Plock和μlock。他們在參數變化區間內峰值變化率絕對值均≥10%，最高可達50%，而其他參數對結果的影響較小(≤5%)。

為定量評價各參數對計算結果穩定性影響的敏感度，以0.515 m/kg1/3處的測點峰值的變化率M(x)作為目標函數，在某個參數變化率x=xi(i=1，2，3，4，5，對應的xi=-0.4，-0.2，0，0.2，0.4)處，目標函數M(x)對該參數變化率xi的敏感度Si可表示為[13]：

Si=?M(x)/?xi

(13)

式中：敏感度Si表示M(x)在x=xi處的導數值，Si的絕對值越大，表示M(x)對xi越敏感。

圖11～12中各曲線大多呈線性或者拋物線變化，因此目標函數M(x)可按照多項式進行擬合，則不同參數的目標函數M(x)與參數變化率x的關系可表示為：

M(x)=a0+a1x+a2x2+…+anxn

(14)

將式(14)代入式(13)，可得：

(15)

參數變化率x區間內包含5個參數，即x=-0.4，-0.2，0，0.2，0.4，可取式(15)中絕對值的最大值來表示該參數的敏感度S：

S=|Si|max

(16)

式中：Si為不同參數變化率xi處的敏感度，i=1，2，3，4，5。

根據式(14)～(16)，將圖11～12中各曲線數據利用Matlab軟件按照多項式進行擬合，擬合精度設在95%以上，之后求導并代入參數變化率xi，最終得到本模型各參數的敏感度S，見表3。

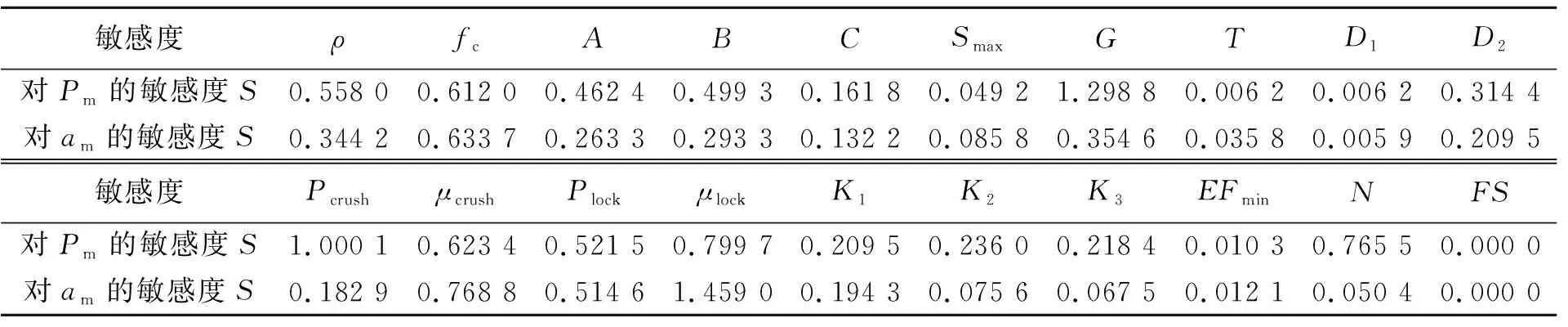
表3 參數敏感度Table 3 Parameter sensitivity

表3定量給出了本模型對計算結果(峰值壓力Pm和峰值加速度am)的敏感度，可見在HJC本構所有參數中，敏感度S>0.4的參數有：ρ、fc、A、B、G、Pcrush、μcrush、Plock、μlock和N，這同圖11～12中峰值變化率大于或等于10%所對應的參數基本上能保持一致。

相比于侵徹類與碰撞類問題的模擬[10, 12-14]，對爆炸類模擬結果影響較大的HJC參數有很多，且對于不同的研究對象影響的程度也不同，其中除了極限面參數A和B之外，還涉及到狀態方程中的三個參數μcrush、Plock和μlock，為此在模擬爆破類問題時，這些敏感度較大的參數需要結合實驗結果來確定，而對于敏感度較小的參數可采用本文中所給的值，以減少重復實驗確定參數的繁瑣過程。

4 結 論

(1)采用SPH-FEM耦合法模擬炸藥在混凝土中爆炸，能直觀地展示了混凝土爆坑形態發展的全過程，固連接觸的方式很好地解決了SPH法在處理邊界問題上的缺陷，同時SPH-FEM耦合法計算的效率也較高。(2)給出了C30混凝土HJC模型各參數的確定過程，并基于確定的參數使用SPH-FEM耦合法對混凝土爆破成坑現象進行了模擬，計算結果與實測數據比較吻合，故所提出的HJC本構參數比較合理。(3)HJC本構參數對峰值壓力和峰值加速度均有較大影響的參數主要有ρ、fc、A、B、μcrush、Plock和μlock，故在模擬爆破類問題時，這些敏感度較大的參數需要結合專門實驗加以確定，而對于敏感度較小的參數可采用本文建議值。