基于近鄰距離加權主元分析的故障定位

郭小萍, 李克勤, 李 元

(1.沈陽化工大學 信息工程學院, 遼寧 沈陽 110142)

隨著現代工業的快速發展，為保證工業生產的安全、高效，工業過程監視與故障診斷變得越來越重要.在現代復雜工業過程中，由于集散控制系統的應用，獲取了大批次的生產過程數據，使得基于數據驅動的過程狀態監視與故障診斷成為研究熱點[1-3]，故障定位也得到了越來越多的關注和重視.

對于多元統計過程監視最常用的方法為偏最小二乘(Partial Least Square，PLS)法[4-5]與主元分析(Principal Component Analysis，PCA)法[6-7].其中PCA法將工業生產過程在正常條件下產生的原始高維數據進行數據特征提取并降維，建立監視模型，得到控制限.若檢測樣本的監視統計量超過該控制限，就認為此刻發生故障[8].在檢測到過程故障后，可以通過定位的方法確定引起故障的變量，找出故障源.對于故障定位，貢獻圖分析法是最常用的一種方法，通過求待測樣本各個變量對監視統計量的貢獻值并做出柱狀圖進行對比分析，認為貢獻值大的變量為故障變量[9].Alcala C F等人[10]提出了一種重構貢獻法，可以明顯提高單變量故障的診斷效果.但做貢獻圖分析時，由于變量之間的相互影響，導致非故障變量的貢獻值變大，引起拖尾效應，容易造成誤診.Van等人[11]運用數值例子對重構貢獻(Reconstruction Based Contribution，RBC)法產生的拖尾效應進行驗證分析.葉昊等人[12]考慮了不同變量間貢獻值的影響，將權值的概念引入到RBC法，提高了診斷效果.LIU J L等人[13]提出了一種基于改進貢獻圖(Modified Contribution Plot，MCP)的故障定位法，將所有檢測樣本的各個變量的貢獻值作出矩陣圖，可以連續直觀地體現出連續過程所定位出的故障變量.但是該方法并沒有改善PCA本身存在的檢測率較低的缺點.

本文提出了一種加權PCA故障定位方法.對正常工況樣本進行加權，強化正常工況變量特征，以加權后的樣本建立PCA模型，計算并確定過程監視綜合統計量[10]及其控制限，判斷是否發生故障.對故障發生時刻的變量采用改進重構貢獻(Modified Reconstruction Based Contribution Plot，MRBCP)法[14]進行故障定位，對每個變量進行逐個重構、檢測，反復迭代分析，直至所有發生故障的變量被定位出來.最后通過仿真實驗研究，與基于PCA的MRBCP方法進行比較，該方法降低了漏報率，并能準確定位出所有故障變量.

1 基于主元分析的故障定位

1.1 主元分析

(1)

(2) 計算X的協方差矩陣RX，X為標準化處理后的矩陣.

(2)

(3) 求解協方差矩陣RX的特征值λ與相對應的特征值向量p，λi是RX的第i個特征值，假設滿足λ1≥λ2≥…≥λn，pi是對應于λi的特征矢量.

|λI-RX|=0

(3)

|λiI-RX|pi=0,i=1,2,…,n

(4)

(4) 根據累計貢獻率選擇相對主元個數，累計貢獻率常取85 %.

(5)

其中，k為選取的主元個數.

1.2 過程監視統計量

將矩陣X分解成式(6)所示.

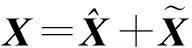
(6)

(7)

(8)

1.2.1 HotellingT2統計量

T2統計量的計算公式[1]為

T2=XPΛ-1PTXT=XDXT

(9)

式中，Λ表示由前k個特征值構成的對角陣.

1.2.2SPE統計量

SPE統計量的計算公式[1]為

SPE=X(I-PPT)XT

(10)

采用核密度估計方法求得SPE統計量的控制限SPEα.

1.2.3φ統計量

φ統計量的計算公式[1]為

(11)

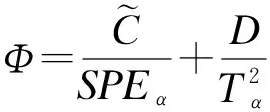
(12)

控制限φα為

(13)

其中：

(14)

(15)

(16)

(17)

1.3 重構貢獻法

當故障發生時，對于單變量發生的故障，故障變量x可以分為正常部分和故障部分，如式(18)所示:

(18)

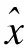
yi=x-ξifi

(19)

由式(19)可以得到重構變量yi的監視統計量:

(20)

式中，M為矩陣代號，當M=PΛ-1PT時，計算的是T2統計量; 當M=I-PPT時，計算的是SPE統計量; 計算綜合統計量時，M=Φ.

通過使重構樣本的監視統計量D(yi)最小，可獲得故障幅值fi，對式(20)求偏導:

(21)

得到幅值公式:

(22)

在進行故障定位時，當定位的故障方向ξi準確時，重構樣本監視統計量D(yi)會低于控制限φα，若高于控制限則表示定位不準確.

重構貢獻率最大時所對應的變量為故障變量.重構貢獻率為單個變量重構貢獻值所占的比重.單變量的重構貢獻值計算如下:

(23)

對于多變量發生故障時，多變量的重構貢獻值為[17]:

cRBC=xMΞ(ΞTMΞ)-1ΞTMxT

(24)

式中，Ξ為故障方向構成的矩陣.如果變量x3、x6為故障變量，則其故障方向矩陣為:

(25)

進行定位時，需要求出對應的故障方向矩陣Ξ，使RBC值最大，若Ξ定位不準確，則RBC值會較小.

2 基于近鄰距離加權PCA的故障定位方法

2.1 基于樣本最近鄰距離的加權方法

正常工況下的樣本進行標準化之后，要進行加權運算，采用樣本間的相似性特征強化正常樣本的特征.加權因子的選擇有多種方法，本文提出一種將正常樣本間歐氏距離作為加權因子的方法，如式(26)所示.

(26)

式(26)中d為m×m的各個樣本間歐氏距離矩陣，取每個樣本與其最近樣本的距離，設每個樣本與其最近樣本間的距離構成的向量為W，則定義正常樣本加權變換矩陣為:

XW=diag(W)·X

(27)

式(27)中，XW為加權后的矩陣，可以采用PCA方法對XW進行分析，建立加權PCA監視模型.

2.2 加權PCA監視模型的建立

過程監視模型的建立過程如圖1所示.

詳細描述如下：

(1) 采集正常工況下的樣本構成樣本集X*;

(2) 采用Z-score標準化法對X*進行標準化處理為X;

(3) 求X中各個樣本間的歐氏距離，將最近鄰距離對樣本進行加權處理為XW;

(4) 對XW進行PCA分析，建立加權PCA監視模型;

(5) 根據式(11)計算統計量φ建模;

(6) 根據式(13)及φ建模確定控制限φα.

圖1 過程監視模型流程圖

2.3 過程監視與故障定位

對于實時采集的樣本，其過程監視與故障定位的流程如圖2所示.

圖2 過程監視與故障定位流程

詳細描述如下:

(1) 對于檢測樣本，采用建模樣本的均值和方差對其進行標準化處理；

(2) 采用建模樣本間的最近鄰距離進行加權處理；

(3) 利用加權PCA模型計算檢測樣本的統計量φ檢測；

(4) 判斷φ檢測是否高于控制限φα，若高于，則進行(5)；反之，則采集下一樣本；

(5) 定義一個空集Xf=φ作為故障變量集合，故障變量的個數定為0，暫未定位的變量認為非故障變量;

(6) 將Xf與變量1(第一個非故障變量)組合；

(7) 求出該組合的最大RBC值，并將其對應的變量加入Xf;

(8) 利用式(20)計算Xf的重構監視統計量D(y)，式(20)中取M=Φ，判斷D(y)是否低于控制限φα，若低于則進行(10)；

(9) 反之，則將Xf中的故障變量與下一個未被定位的非故障變量組合，回到步驟(7)繼續循環定位; 依次迭代.

(10) 求各變量的貢獻率，做出貢獻圖，完成定位.

3 仿真研究

3.1 數值案例

設數值案例有20個變量xi,i=1,2,…,20，該過程模型[18]為:

x=Gt+e

(28)

xf=x+Ξf

(29)

式中，Ξ為多變量故障的方向向量構成的矩陣，f為故障幅值，從第100個樣本開始，對3個變量x1、x8、x18都加一個幅值f=2的故障.

基于加權PCA的MRBCP方法應用于數值例子的故障定位分析如圖3所示.橫縱坐標分別表示樣本檢測時刻和變量，彩色帶表示重構貢獻率，重構貢獻率大的變量則被認為是故障變量.

從圖3可以明顯看出在100時刻之后，變量x1、x8、x18的重構貢獻值明顯較大，3個故障變量能夠清晰準確地被定位出來.

圖3 加權PCA法應用于數值案例的貢獻圖

3.2 TE過程仿真

TE(Tennessee Eastman)過程是一個對TE化學公司實際生產裝置的真實模擬，是一個典型的多變量連續復雜過程，被廣泛應用于過程故障診斷[19].TE過程包括5個主要操作單元:反應器、冷凝器、循環壓縮機、氣液分離器、汽提塔；包含8種成分:A、B、C、D、E、F、G及H.該過程有12個操縱變量和41個測量變量，其中41個測量變量包括19個成分測量變量和22個連續過程測量變量.現對22個連續過程測量變量進行研究.TE過程有20個故障類型，采用的建模樣本由正常工況下22個變量的500個采樣構成；采用的檢測樣本由故障工況下22個變量的960個采樣構成，對故障1和故障14進行試驗.故障1[20]和故障14[14]的故障變量如表1，并且均從160時刻發生故障.

表1 故障變量

為了驗證加權方法對樣本產生的影響，作出加權前后的樣本分布圖進行比較.圖4是建模樣本160～500時刻的分布圖，圖5是故障1的檢測樣本160～960時刻的分布圖.由圖可以看出樣本加權之后，樣本分布范圍雖然被整體放大，但是樣本間分布卻更加緊密，放大了變量的個體特征，降低變量之間的相互影響，可以使變量被逐個定位時更加準確.

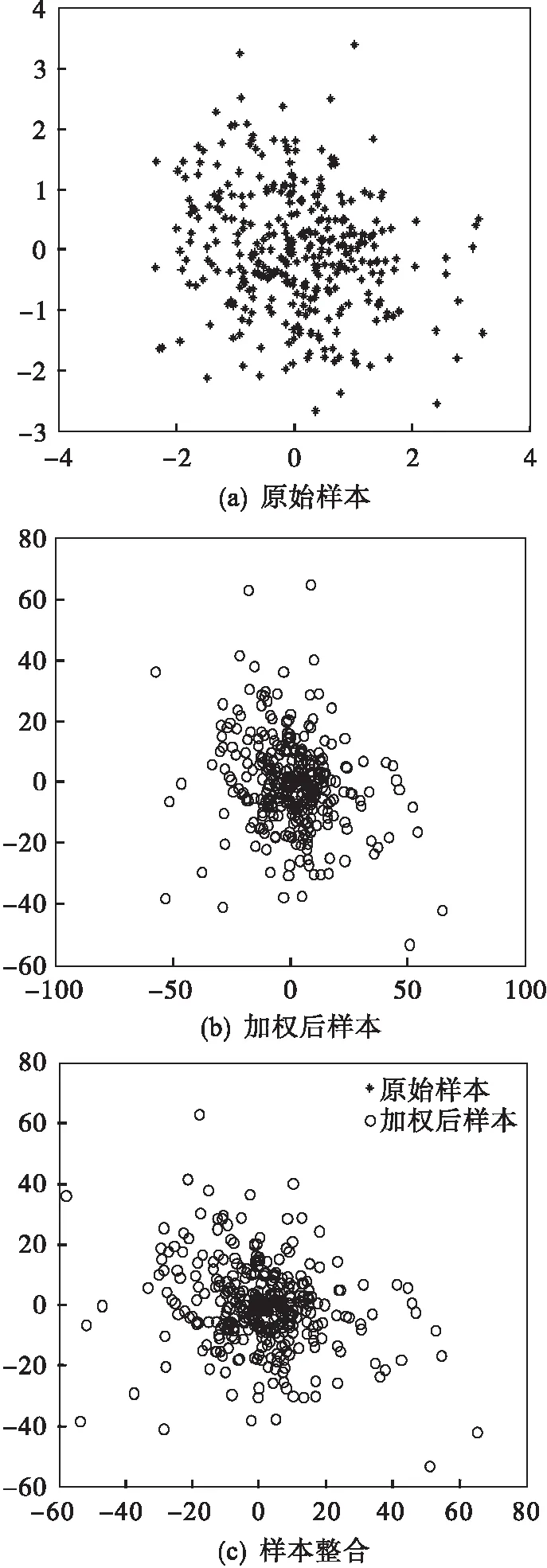
圖4 建模樣本分布圖

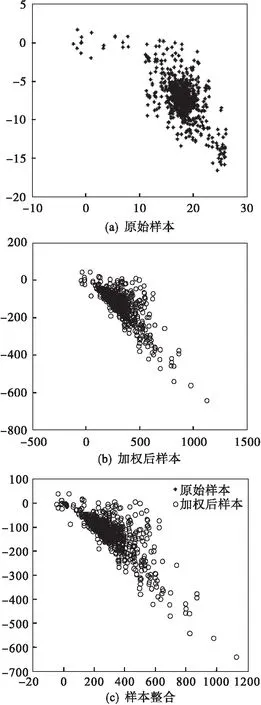
圖5 監測樣本分布圖

基于PCA的MRBCP方法、基于加權PCA的MRBCP方法對TE過程故障1的故障定位分析如圖6、圖7所示.故障發生初期，即160時刻到大約400時刻，由于各變量之間的相互影響，無法準確定位出故障變量.400時刻以后，由于控制系統的調節，可使系統達到新的穩定.從圖6可以看出基于PCA的MRBCP方法只能定位出一個故障變量，而圖7基于加權PCA的MRBCP方法可以準確定位出所有故障變量，大大降低了漏報率.同時，降低了非故障變量對故障變量的影響，避免了定位出非故障變量的誤報情況，定位結果明顯、準確.

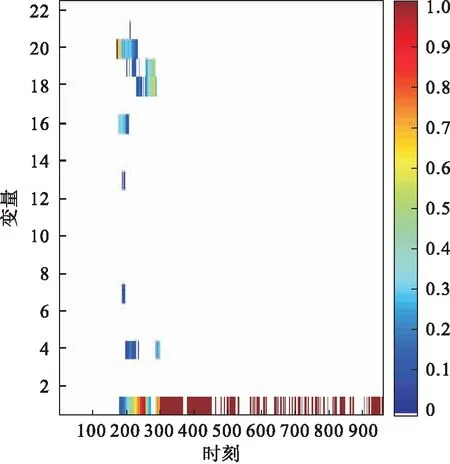
圖6 故障1基于PCA方法的貢獻圖

圖7 故障1基于加權PCA方法的貢獻圖

基于PCA的MRBCP方法、基于加權PCA的MRBCP方法對TE過程故障14的故障定位分析如圖8、圖9所示.雖然基于PCA的MRBCP 方法對于故障14也能準確定位出所有故障變量，但是可以明顯看出在發生故障時刻之后，并不是每一時刻都可以檢測到故障，有較高的漏報率.而采用加權PCA的MRBCP方法時，發生故障后，每一時刻都可以檢測出故障，降低了漏報率.故障1在400時刻之后的漏報率如表2所示.故障14在400時刻之后的漏報率如表3所示.

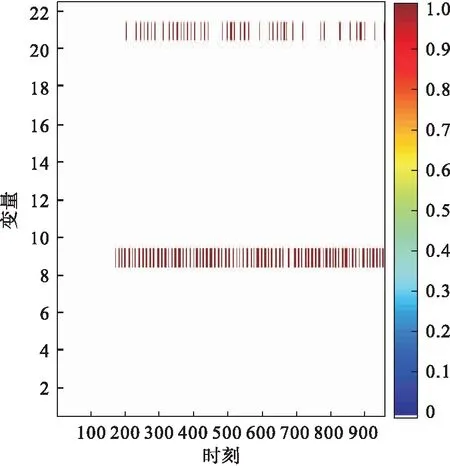
圖8 故障14基于PCA方法的貢獻圖

圖9 故障14基于加權PCA方法的貢獻圖

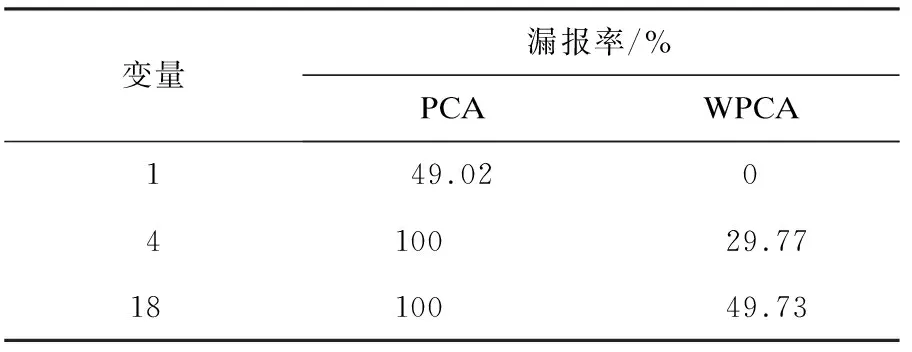
變量漏報率/%PCAWPCA149.020410029.771810049.73

表3 故障14漏報率對比表

為了進一步驗證所提方法的正確性，在式(24)中，將每個故障方向(Fault Direction)向量逐步加入故障方向矩陣Ξ.以故障14為例，圖10為故障14的逐步重構監視結果.可以看出在160時刻后，原始樣本的監視值高于控制限，加入一個故障方向向量進行重構后，監視值更接近控制限.直至所有故障變量加入故障方向矩陣中，重構樣本的監視值低于控制限，說明所有故障變量都被重構為正常變量，即所有的故障變量被定位出來，驗證了被定位故障變量的準確性.

圖10 故障14逐步重構監視結果

4 結 論

提出了一種將正常工況下樣本間最近鄰距離作為加權因子對樣本進行加權的方法，采用綜合統計量作為監視統計量，在多變量發生故障的情況下，與基于PCA的改進重構貢獻圖的故障定位方法進行對比，所提方法定位準確并降低了漏報率.但是，該方法通過對貢獻率的大小判斷變量是否發生故障，忽略了貢獻率低的變量，其是否為故障變量仍需進一步研究.