無人機軟連接吊艙的偽衛星定位算法研究

榮鳳娟,張清華,張杰,徐鍵卉

(陸軍工程大學,江蘇 南京 210007)

0 引 言

近年來,多旋翼無人機技術與裝備發展迅猛,其靈活易操作特性使得許多科研項目選用它們作為載體[1-3],然而,某些科研儀器為了避免電磁干擾和物理震動,需與無人機機身保持距離,利用吊艙把科研儀器和無人機進行軟連接是一種較好的選擇[4-5]。通常情況下無人機自帶有單頻的衛星導航天線,但軟連接情況,承載儀器的吊艙和無人機的相對關系受外界環境和風力影響,不能保持準確的相對位置關系,故需要對吊艙進行單獨定位,以得到科研儀器的動態精確位置[6-7]。衛星定位為常見的實時高精度定位手段,但是在復雜環境下,如衛星可見性較差的,將無法定位,偽衛星是一種較好的可以靈活布設發射基站的定位設備,GPS作為常見定位手段,但在衛星可見性較差情況下無法定位,而偽衛星可以應對此類情況[8-9]。本文擬利用2.4 GHz無線測距裝置作為偽衛星定位設備,在一定條件約束下對偽星的空間最優布設效果進行仔細深入的分析,并采用擴展卡爾曼濾波來應對偽衛星定位中的非線性問題,同時對定位結果與GPS進行了比較分析。

本論文的結構安排如下:第二章介紹了偽衛星定位設備的原理;第三章介紹了應用中偽衛星的定位算法,重點介紹了處理線性問題的擴展卡爾曼濾波算法,第四章為野外試驗分析,包括現場的設置情況、空間星座分布的評估結果以及最重要的定位結果精度分析;第五章為總結和結論,從技術方法和工程試驗效果等方面對本文的工作進行了評價,并分析了不足和下一步需要改進的技術方法。

1 偽衛星定位設備及定位原理

1.1 硬件組成

項目采用的是某公司提供的偽衛星系統,該系統的控制系統可以在一個標準筆記本電腦上流暢運行,它包含多個偽衛星發射裝置(RN),并且具有測量距離的功能,同時還具有一個負責通信的終端(GW),測定兩計算接收機(MN)的位置的距離,如圖1所示。

在試驗中采用了兩種偽衛星發射終端,其中終端1既可以作為偽衛星發射基站,如圖2(a)所示,又可以作為接收機使用,終端2只可以作為接收機使用,如圖2(b)所示。

1.2 定位基本原理

與GPS定位的原理類似,該定位系統也是基于空間后方交會。偽衛星單點定位是以偽衛星發射基站和用戶接收機天線之間的距離觀測量為基礎,并在已知精確偽衛星坐標的基礎上來確定接收機天線所對應的觀測點的坐標(x,y,z)。

則對于第i個偽衛星,它與接收機天線之間觀測得到的距離量為

(1)

式中:Si為偽衛星和接收機之間的距離量,而第i個偽衛星的坐標(Xi,Yi,Zi)事先精確已知,則求解接收機坐標(x,y,z)至少需要三個以上的偽衛星。假設有三臺以上的偽衛星同時對接收機觀測(n≥3),則有以下線性化后的方程

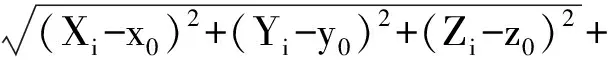
(2)

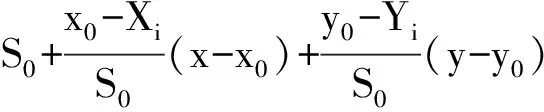
(3)

L=Hx+δ,

(4)

1.3 偽衛星空間分布評價(DOP)

DOP具有測量和代數的雙重含義:在測量中代表GNSS衛星的幾何結構所引起的偽距定位誤差的比例,在代數中反映最小二乘平差權逆陣的跡特性。

在公式(4)中,設計矩陣為

(5)

式中:axi,ayi,azi(i=1,2,…,n)為接收機位置與偽衛星位置之間方向矢量的余弦,假設P為單位矩陣,則式(9)有如下形式

COV(x)=(HTH)-1σ2.

(6)

則PDOP、HDOP、VDOP可以由如下公式來表示

(7)

DOP值越小,則估計值x的協方差陣就越小,即具有更高的參數估計精度。

2 偽衛星動態定位的EKF算法

偽衛星定位系統與 GNSS 最大的不同點是偽衛星發射器一般距離用戶接收機相對較近,這可能給定位過程帶來一些有利的影響,例如不用考慮電離層對偽衛星觀測量的影響,但是同時也會帶來一些不利的影響,例如遠近效應和線性化誤差等。

在用濾波方法消除衛星定位數據中的隨機誤差時,可以使用最優估計的方法,將真實的狀態(定位結果)從各種隨機干擾中實時最優估計出來,但應用不同濾波器進行最優估計(濾波)時,需要建立較準確的系統模型和觀測模型,而且要對各種隨機誤差進行準確地建模。目前國內外對將最優估計方法應用于濾波方面做了大量的研究,也取得了很多相應的成果。

通常最小二乘方法不考慮觀測信號的統計特性,僅僅保證測量誤差的方差最小。同時,最小二乘法的迭代僅僅考慮了當前的信號狀況,沒有涉及前面的信號狀況。因此在偽衛星定位的過程中,對定位結果計算的穩定性估計不足。

設動態系統的狀態方程和測量方程分別為:

Xk=Φk,k-1Xk-1+Γk,k-1Wk-1,

(8)

Zk=HkXk+Vk.

(9)

為了減少線性化誤差,學者們使用擴展卡爾曼濾波(EKF)。在考慮了泰勒展開的二階項的條件下,二階擴展卡爾曼濾波能使濾波性能得到改善。但是由于要同時計算雅克比矩陣和漢森矩陣,使得濾波計算量和不穩定性都大大增加。

EKF基于模型和觀測模型統計信息,提供系統狀態最小方差估計。狀態方程和測量方程在其前一估計處進行線性化處理:

(10)

從而將非線性系統轉換成線性離散系統形式,再利用線性卡爾曼濾波器進行估計。其算法具體實現如下[12]:

時間更新:

(11)

測量更新:

(12)

其中,Kk被稱作卡爾曼濾波增益

(13)

雖然時間更新和測量更新中狀態分別用非線性方程表示,但協方差陣使用線性化的方程進行傳播。

3 野外試驗分析

3.1 現場設置

為了對本試驗中的六旋翼無人機軟連接吊艙進行動態定位分析,本文的研究人員選取了位于南京湯山地區的一塊平坦區域進行場地試驗(如圖3所示)。首先在場地的周圍架設6個高度約15 m的鐵塔,用于安裝偽衛星基站的天線,而基站的初始位置由全站儀進行確定,其平面位置如圖4所示,具體的基站坐標如表1所示。

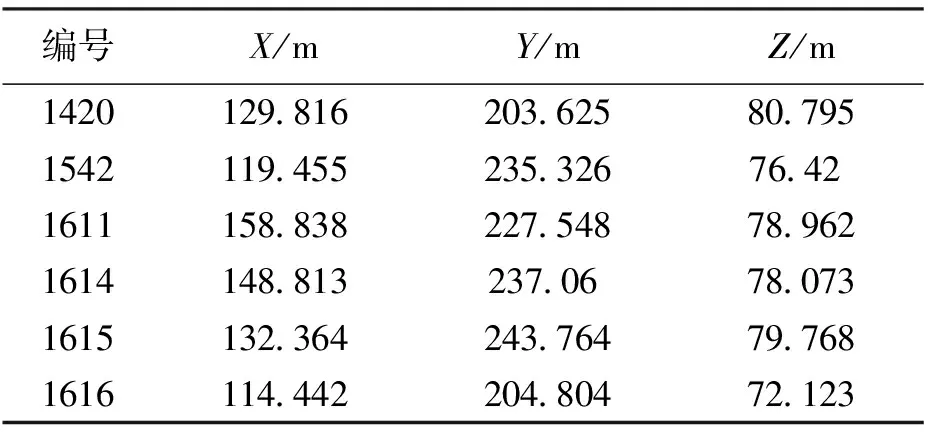
編號X/mY/mZ/m 1420129.816203.62580.795 1542119.455235.32676.42 1611158.838227.54878.962 1614148.813237.0678.073 1615132.364243.76479.768 1616114.442204.80472.123

為了對偽衛星定位的效果進行分析,試驗采用GPS RTK 技術與偽衛星定位結果進行比對,以驗證偽衛星定位的絕對精度。試驗中將偽衛星觀測站(OS)與GPS RTK天線采用捆綁的方式固定在一起,并利用軟連接與無人機進行連接(如圖5所示)。而圖6為正在進行的動態定位試驗,無人機飛行的范圍在由鐵塔圍成的多邊形區域內部。

3.2 空間星座構型

根據基站布設的位置,利用2.3節中的DOP值理論對試驗場內的基站空間分布情況進行評價。其中圖7(a)的淺色線條為無人機的飛行軌跡。圖7(b)、7(c)和7(d)分別為PDOP、HDOP和VDOP的分布情況,可以發現,無人機的飛行區域基本位于DOP值較為理想的區域,非常有利于試驗的開展。

3.3 定位結果分析

利用EKF算法對無人機軟連接下的偽衛星觀測站進行了動態定位,同時利用GPS RTK得到共位坐標。圖8(a)～圖8(d)分別表示了偽衛星和GPS定位三維和X、Y及Z方向的定位結果比較,通過比較可以發現,在絕大多數的時間內,二者定位的結果都比較吻合(如圖8(a)所示),但在圖8(b)的30～40 s的時間段內(灰色區域),偽衛星和GPSR TK的定位結果出現了較大的差異,此差異可能是由于無人機在X方向機動較快,而造成了偽衛星定位精度的降低。

為了進一步分析二者的差異,對偽衛星和GPS的定位結果進行差分比較,通過分析圖9可以發現,偽衛星在X方向的定位結果比Y和Z方向略差,X方向是無人機行進過程的主要方向,相當于徑向,其機動性最強。而且在X方向還存在數據跳變(Data jitter)的情況,這可能是偽衛星基站的不穩定造成的。對于誤差分布,在X方向一定時間段內還存在著明顯的誤差漂移(Error drift),這可能是基站在X方向測距存在著累積誤差。對于精度更好的Y和Z方向,其在無人機的起飛和降落階段,同樣存在著較大的誤差(Larger errors),這可能是無人機初始運行的時候,機動性能較強且存在無固定規律的抖動造成的。

以GPS RTK測量結果為真值,對偽衛星定位誤差絕對值的統計結果見表2.其中,X方向的最大誤差為0.5 m左右,Y和Z方向的最大誤差為0.2 m左右,三維方向的最大誤差為0.5 m左右。三維平均誤差優于0.2 m,標準差為0.15 m左右。偽衛星的定位精度基本可以滿足未爆彈探測定位無人機對吊艙定位的需求。

表2 定位誤差絕對值統計

4 結束語

針對六旋翼無人機軟連接吊艙的動態定位問題,論文在野外試驗場地搭建了偽衛星定位系統,并利用EKF算法對吊艙的實時位置進行了估計。同時,試驗中采用了GPS RTK定位的結果對偽衛星定位結果進行了評估,結果表明,采用此偽衛星系統及EKF算法可以在三維方向達到5 cm左右的精度,完全可以滿足復雜條件下的無人機吊艙定位,可以很好地運用到實際工程中,為無人機定位提供了新的手段和方法,具有重要的意義。

但是,在無人機起降及機動性強的時間段,偽衛星的定位都存在較大偏差,需要在以后的研究中通過物理模型和數學加以改進。此外,偽衛星基站的持續穩定供電,也是下一步需要著重研究的工程化問題。