GPS高程擬合方法對比研究分析

方蘇陽,趙勇

(1.安徽理工大學 測繪學院,安徽 淮南 232001;2.華東有色測繪院,江蘇 南京 210000)

0 引 言

隨著GPS技術逐漸成熟,GPS被廣泛運用到人們生產和生活的各個部門[1-2],在測繪領域的運用更是廣泛。GPS技術集數據采集、處理、傳輸、分析于一體[3-4],在測繪領域主要由于其高精度的定位而被運用到建立各級平面控制網中,卻不能在高程測量中得到很好的運用。由于GPS高程測量是在大地高系統下以參考橢球為基準面,而生活中需要用到的高程是在正常高系統系下以大地水準面為基準面測得[5],由于不同的基準面,GPS高程測量所得到的大地高不能在工程中直接使用。針對上述問題,眾多國內外學者對GPS高程擬合深入研究,獲得豐碩的研究成果。例如田曉[6]針對高程擬合模型不同的特點,研究了適用于不同地形特征的GPS高程擬合模型,經試驗表明,該模型相對于其他模型具有更高的擬合精度,所得出的殘差更穩定;史俊莉[7]通過分析地形對GPS高程擬合精度影響問題,將地形改正引入到了GPS高程擬合中,有效解決因短波分量的計算問題,提高了擬合精度;魏宗海[8]改進了BP神經網絡算法,通過不同的指標評價擬合結果,實驗結果表明,不同算法改進BP網絡模型能夠有效地提高擬合精度和效率。

由于不同的GPS高程擬合模型普適性低,在不同環境下具有一定局限性,難以將模型優勢充分利用。考慮到上述問題,本文研究多種GPS高程擬合模型,通過實例分析研究模型在高程擬合方面的應用及其對應的局限性,總結出了針對不同情況下獲取的數據所采取的不同擬合方法,以獲得高精度的高程轉換。研究成果對GPS高程測量在不同環境下的工程項目中的推廣具有較好的參考價值。

1 GPS高程擬合模型研究

1.1 二次多項式曲線擬合法

多項式曲線擬合[9]將測區認定為不規則分布曲線,利用m次的代數多項式插值處理,將測線方位作為X軸,將測線垂直方位作為Y軸,令高程異常為ζi,利用下列m次多項式擬合。

ζi(xi)=a0+a1xi+a2xi2+…+amxim,

(1)

式中,xi為擬合點至參考點(x0,y0)直線距離。

(2)

各高程控制點的已知高程異常與其擬合值之差i被稱為離差:

ri=ζi(xi)-ζi,i=1,2…，n.

(3)

即在已知點處的離差ri的平方和最小:

(4)

這樣的條件下求解ai,接著求出各點的ζ,從而獲得正常高。

1.2 多面函數擬合法

多面函數擬合法[10]本質是數學曲面逼近的方法,基本思想是用數學表面逼近所測區域的大地水準面。利用數學模型所建立的水準面面精度高,能夠有效地代替真實水準面,利用數學模型在各插值點之間建立函數關系,并將函數疊加,組成多面函數,由于這是每個插值點與已知數據建立的函數關系,因此多面函數具有計算最佳擬合值的特點,因此多面函數曲面擬合法就能夠更準確地擬合出未知點的高程擬合值。

多面函數的數學表達式為

(5)

式中：ai為待定系數；Q(x,y,xi,yi)為核函數；x,y為待求點的坐標；xi,yi為已知點坐標,是核函數中心所在地方。

理論上核函數是可以任意構造的,在實際應用中,較常用對稱性的距離函數,通常用以下幾種函數來充當核函數:

1) 錐面:

Q(x,y,xi,yi)=C+[(x-xi)2+

(y-yi)2]2.

(6)

2) 雙曲面:

Q(x,y,xi,yi)= [(x-xi)2+(y-yi)2+

(7)

3) 倒曲面:

Q(x,y,xi,yi)= [(x-xi)2+(y-yi)2+

(8)

4) 三次曲面:

Q(x,y,xi,yi)=C+[(x-xi)2+

(9)

上面幾種函數中,x,y表示內插點坐標,xi,yi為已知點的坐標,(x-xi)2+(y-yi)2為內插點到已知點的水平距離,式中的參數δ為光滑系數。當已知待求點的點數時,任意一點ζp為

ζp=QpQ-1ζ

=(Q1p,Q2p,…,Qnp).

(10)

式中,Qij=Q(x,y,xi,yi) .

(11)

當已知點數少于待求點數時,

ζp=Qp(QTQ)-1QTζ.

(12)

已知點的高程異常值ζ為直接關系到未知點的高程異常值ζp的計算結果,因此,如果想要更好地結算出未知點的高程異常值,必須認真選取已知點,并且使所選的已知點的高程異常值相差比較大,因為這些點能最好地描述地形變化特征,即高程異常值的分布特征。這些特征點的選擇一般在地勢高和地勢較低的地方。在選擇多面函數求解測區內點的高程異常值的時候,需要注意的是核函數的選取問題,由于其取值是自主取值,為了能達到擬合最佳效果,就要逐步地試驗改進,然后選定一個最佳取值(本文經多次反復實驗,選擇三次曲面函數作為核函數)。

1.3 二次曲面擬合法

多項式曲面擬合常用于測區控制點大面積面狀分布,利用二次曲面擬合模型[11]進行擬合,可得到公共點上的高程異常與平面坐標之間的關系，其表達式為

(13)

式中:a0,a1,a2,a3,a4,a5為待定參數。

1) 區域內只有6個公共點。

ζ=XA,

(14)

其中,

求解待定點的高程異常值關鍵在于確定多項式的系數,常用的方法為高斯消元法。確定完多項式,將待定點代入多項式中,求出高程異常值,繼而求解正常高Hr.

2) 當公共點多于6個時,則可列出相應的誤差方程:

a5xiyi-ζi,i=1,2…，n.

(15)

寫成矩陣形式為

V=XA-ζ.

(16)

在離差的和∑V2為最小值的條件下,根據最小二乘法原理可求得A,然后就可以求出任一點的高程異常值ζ,從而求出Hr.

1.4 BP神經網絡法

神經網絡通過大量觀測數據構成的樣本集的學習與仿真,保證了神經網絡對沉降數據預測的準確性,BP神經網絡是具有三層(及以上)神經元的神經網絡,其中有輸入層、隱含層以及輸出層[12-14]。輸入層輸入樣本集,每一個樣本集組成一個神經元,神經元激活值通過隱含層正向傳播至輸出層,學習過程中反復修改神經元權值,若輸出的結果滿足期望,則認為學習過程結束,可以進行數據預測,若與期望存在一定差距,則需要調整神經網絡相應參數。結合高程擬合的BP網絡結構圖如圖1所示。

圖中,輸入層為GPS高程擬合點平面坐標,學習信號為已知點的高程異常ζ′,輸出層為所求GPS高程擬合點的高程異常ζ.

對于BP神經網絡來說,選擇隱含層節點數十分重要,隨著隱含層節點的增加,網絡能夠更好地解決非線性問題,但同時也會引起網絡收斂速度慢,增長網絡學習時間,所以隱含層存在一個臨界節點數。選擇隱含層節點個數十分復雜,目前常用的方法有如下幾種:1) 通過輸入層節點數確定。2) 根據輸入層與輸出層節點個數確定。

BP神經網絡算法可以分為以下幾個部分:

1) 初始化BP網絡,確定輸入層、隱含層、輸出層節點數,分別設為n、i、m;初始化各層連接權值,令隱含層與輸入層連接權值為ωij、隱含層與輸出層之間的連接權值ωjk;分別初始化各層神經元的閾值,設隱含層閾值為aj(j=1,2，…),輸出層閾值為bk(k=1,2，…)。給定學習數據集,即提供輸入向量(學習樣本)以及期望輸出向量(高程異常)。

2) 計算出隱含層輸出M.

(17)

式中，f函數表示激勵函數。

3) 根據計算得出的隱含層輸出M,計算出輸出層輸出S.S為BP神經網絡算法學習輸出的高程異常(未檢核)。

(18)

4) 計算均方誤差ε,

ε=Yk-Sk.

(19)

5) 反復更新權值與閾值,根據上述所求得的高程異常預測誤差ε,更新連接權值ωij、ωjk以及閾值aj、bk公式為

i=1,2…,j=1,2，…,

(20)

ωjk=ωjk+μMjek,j=1,2，…,k=1,2，… ,

(21)

j=1,2，… ,

(22)

bk=bk+ek,k=1,2，… .

(23)

6) 最后是判斷過程,若算法輸出高程異常值滿足精度要求則結束迭代,若未滿足要求則返回2) 繼續迭代。

通過反復迭代,利用BP神經網絡進行GPS高程擬合具有很高的精度。

2 工程實例應用

2.1 研究區概況

將某市GPS工程控制網數據為高程擬合實驗數據。該地區地形平緩,以平原為主。該控制網控制點數為270個,控制點分布不均勻,選取測區內共有30個GPS水準聯測點,該測區幾何水準測量為四等水準測量。選取該測區中精度高低不等且分布均勻的25個GPS控制點作為本次試驗處理數據,點位分布以及具體數據如圖2和表1所示。

點名XY水準高程/mGPS高程/m高程異常ζ A1518 919.0643 645 477.49344.275 656.585 712.310 1 A2521 948.2063 644 145.27453.642 565.917 912.275 4 A3527 095.7713 649 661.43929.450 541.741 912.291 4 A4526 079.4523 645 417.60645.754 158.049 712.295 6 A5525 975.1213 642 769.16136.426 348.732 712.306 4 A6526 306.9373 641 029.06136.785 649.106 912.321 3 A7528 106.6653 641 090.28134.333 846.646 312.312 5 A8528 424.8153 637 219.91639.979 552.260 812.281 3 A9527 646.7233 633 978.78934.004 846.31912.314 2 A10529 423.2513 639 409.85837.523 749.807 312.283 6 A11528 937.9823 642 910.63135.054 747.362 612.307 9 A12530 686.2243 649 840.06329.042 941.340 212.297 3

表1(續)

2.2 高程擬合

實驗檢核點為A4、A6、A8、A11、A16、A17、A19、A21、A23、A24,另15個點作為實驗擬合點。通過本文前述四種擬合模型進行擬合實驗,并進行精度計算,對擬合結果進行對比分析,具體數據分析如表2、圖3、表3所示。(BP神經網絡擬合法所確定的隱含層個數為6,BP網絡為3-6-1模型)。

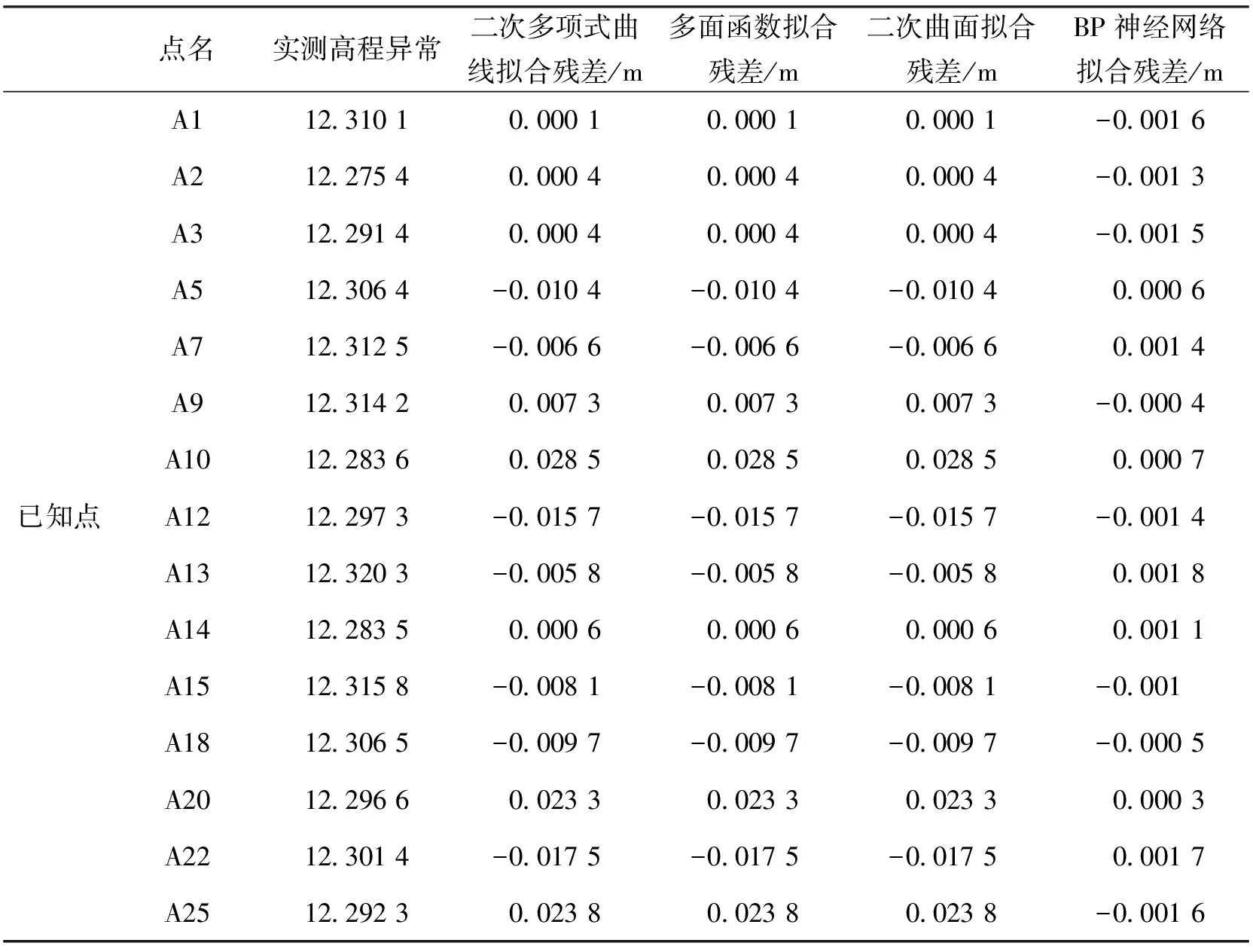
表2 四種高程擬合方法對比

二次多項式曲線擬合/m多面函數擬合/m二次曲面擬合/mBP神經網絡擬合/m 內符合精度: μ=[VV]/(n-1)±0.014 3±0.014 3±0.014 3±0.001 2 外符合精度: M=[VV]/(m-1)±0.016 4±0.013 9±0.014 8±0.001 1

2.3 分析與比較

根據擬合計算結果表3和擬合殘差圖3可知:四種擬合方法進行實驗數據高程擬合都可以滿足四等幾何水準的要求。采用不同的擬合方法,進行擬合后的結果不同,其中的BP神經網絡擬合法較其他方法可以達到較高的精度。

通過二次曲面擬合與二次多項式曲線擬合進行比較可以得出結論:對于測區點為面狀分布時,采用曲面擬合法,更能反映測區的似大地水準面狀況,其精度高于基于曲線的曲線擬合法。

通過多面函數擬合與二次曲面擬合進行比較可以得到結論:測區并不完全是一個規則的起伏面,對二次曲面擬合可能有較大的影響,對測區采用了多面函數的方法進行擬合,多面函數擬合的效果比二次曲面擬合的效果要好,內符合精度和外符合精度都得到了較大的提高。

通過BP神經網絡擬合與二次多項式曲線擬合、多面函數擬合、二次曲面擬合進行比較可以得出結論: BP神經網絡擬合法的擬合精度高于曲線、曲面擬合法的擬合精度。運用BP神經網絡擬合法進行平原區域的GPS高程擬合,具有較高的擬合精度,其數據較好地貼近似大地水準面。故而在位于平原區域的測區進行GPS高程擬合時,可利用神經網絡擬合法的特點,獲得高精度的正常高。

3 結束語

本文通過高程擬合實驗分析對比四種GPS高程擬合方法,研究表明,針對不同測區選擇適當的高程擬合模型能夠提高高程擬合精度;高程異常變化明顯的地區曲線曲面擬合方法精度較低,宜采取多面函數擬合法;BP神經網絡擬合模型在本次實驗中精度高于其余三種擬合模型,可以認為在地形平緩地區,BP神經網絡擬合方法能夠高精度地進行高程擬合。