機(jī)器學(xué)習(xí)技術(shù)在織機(jī)運(yùn)行狀況預(yù)測中的應(yīng)用

侯 濤

為了確保經(jīng)編機(jī)在生產(chǎn)中維持正常運(yùn)轉(zhuǎn),可以通過經(jīng)編機(jī)的歷史運(yùn)行數(shù)據(jù)、實(shí)時(shí)運(yùn)行數(shù)據(jù)和已經(jīng)設(shè)置的織機(jī)運(yùn)行參數(shù)來預(yù)測織機(jī)的運(yùn)行狀況。傳統(tǒng)的預(yù)測分析是在歷史資料基礎(chǔ)上得到客觀規(guī)律,結(jié)合相關(guān)領(lǐng)域?qū)＜业膶I(yè)經(jīng)驗(yàn),預(yù)先對各種可能發(fā)生的運(yùn)行狀態(tài)先驗(yàn)地預(yù)測其概率。但是先驗(yàn)分布具有一定的局限性,先驗(yàn)分布和許多決策問題的準(zhǔn)確性易受到先驗(yàn)信息充分與否的影響,同時(shí)決策人預(yù)先對狀態(tài)可能發(fā)生的概率做出的主觀判斷與客觀真實(shí)情況存在一定的差距。

近年來人工智能技術(shù)發(fā)展迅速,為提高紡織機(jī)械設(shè)備故障預(yù)測技術(shù)的可靠性和有效性,將人工智能相關(guān)技術(shù)引入到紡織機(jī)械設(shè)備故障預(yù)測中來很有必要。本文通過分析經(jīng)編機(jī)故障的性質(zhì)、分類與影響經(jīng)編機(jī)故障預(yù)測的各類指標(biāo),構(gòu)建了經(jīng)編機(jī)故障預(yù)測框架;通過使用主成分分析法對影響經(jīng)編織機(jī)故障預(yù)測的各類指標(biāo)降維處理,構(gòu)建了基于距離判別法的經(jīng)編織機(jī)故障預(yù)測模型,從而實(shí)現(xiàn)了經(jīng)編織機(jī)的故障預(yù)測。

1 經(jīng)編機(jī)運(yùn)行故障預(yù)測的理論基礎(chǔ)

1.1 經(jīng)編機(jī)故障影響因素分析

對影響經(jīng)編機(jī)故障預(yù)測指標(biāo)進(jìn)行分析,以獲得反應(yīng)經(jīng)編機(jī)生產(chǎn)狀態(tài)的特征量,從而采用基于主成分分析和距離判別法理論進(jìn)行經(jīng)編機(jī)故障預(yù)測模型的建立。在對紡織廠進(jìn)行了實(shí)地調(diào)查基礎(chǔ)上,通過對經(jīng)編機(jī)生產(chǎn)運(yùn)行過程的分析,對經(jīng)編機(jī)故障預(yù)測指標(biāo)的建立從離散型數(shù)據(jù)和連續(xù)性數(shù)據(jù)兩方面入手,其結(jié)構(gòu)如圖1所示。

圖1 影響經(jīng)編機(jī)故障預(yù)測指標(biāo)體系

經(jīng)編機(jī)的故障是一個(gè)從正常狀態(tài)到故障的逐步演化的多狀態(tài)過程,將經(jīng)編機(jī)運(yùn)行狀態(tài)分為正常、停機(jī)、換盤、故障、維修。在停機(jī)狀態(tài)下不可能向故障狀態(tài)轉(zhuǎn)變,當(dāng)經(jīng)編機(jī)發(fā)生故障時(shí)運(yùn)行狀態(tài)從正常狀態(tài)向故障狀態(tài)轉(zhuǎn)變,當(dāng)經(jīng)編機(jī)換盤后品種不合適可能會(huì)造成經(jīng)編機(jī)故障。

1.2 主成分分析

主成分分析(PCA)是一種較為成熟的多元統(tǒng)計(jì)監(jiān)測方法。應(yīng)用PCA的方法將顯式變量作一定的線性轉(zhuǎn)化產(chǎn)生數(shù)量較少的隱式變量,降低原始數(shù)據(jù)空間的維數(shù),再從新的隱式變量中提取主要變化信息及特征[1]。這樣既保留了原有數(shù)據(jù)信息的特征,又消除了變量間的關(guān)聯(lián)、簡化分析復(fù)雜度;從新的數(shù)據(jù)空間中提取符合相應(yīng)要求的主元數(shù),同時(shí)也消除了部分的系統(tǒng)噪聲干擾。特征或?qū)傩蕴鄷?huì)增加問題的復(fù)雜程度與難度,主成分分析就是把原來多個(gè)特征化為少數(shù)幾個(gè)特征指標(biāo)的一種統(tǒng)計(jì)分析方法,從數(shù)學(xué)角度看這是一種降維處理[2]。

為了消除量綱的影響,將變量標(biāo)準(zhǔn)化后再計(jì)算其協(xié)方差矩陣。任何隨機(jī)變量對其作標(biāo)準(zhǔn)化變化之后,其協(xié)方差與其相關(guān)系數(shù)是一回事,即標(biāo)準(zhǔn)化后的變量協(xié)方差矩陣就是其相關(guān)系數(shù)矩陣。根據(jù)協(xié)方差的公式可以推得標(biāo)準(zhǔn)化后的協(xié)方差就是原變量的相關(guān)系數(shù),即標(biāo)準(zhǔn)化后的變量的協(xié)方差矩陣就是原變量的相關(guān)系數(shù)矩陣。也就是說,在標(biāo)準(zhǔn)化前后變量的相關(guān)系數(shù)矩陣不變。

主成分分析的計(jì)算步驟如下：

(1)將變量進(jìn)行標(biāo)準(zhǔn)化處理;

(2)計(jì)算相關(guān)系數(shù)矩陣;

(3)求出相關(guān)系數(shù)矩陣的特征值及相應(yīng)的正交化單位特征向量;

(4)選擇主成分;

(5)計(jì)算主成分得分。

1.3 距離判別分析

距離判別法的基本思想是根據(jù)已分類的樣本空間的樣本數(shù)據(jù),計(jì)算出每個(gè)分類的重心即分類均值。若待檢樣本與某類的重心距離最近,就認(rèn)為它是來自于該類。距離判定方式有歐氏距離、曼哈頓距離、切比雪夫距離及馬氏距離等。

馬氏距離的計(jì)算與原始數(shù)據(jù)測量單位沒有關(guān)系,不受指標(biāo)單位不統(tǒng)一的影響,故本文選取馬氏距離作為距離度量公式。馬氏距離能夠有效計(jì)算兩個(gè)未知樣本集的相似度,表示協(xié)方差的距離。其物理意義就是在規(guī)范化的主成分空間中的歐式距離,即首先利用主成分分析將樣本分布改變到另一個(gè)空間,而馬氏距離就是樣本在新空間中分布的歐氏距離。

2 經(jīng)編機(jī)故障預(yù)測運(yùn)行過程

2.1 經(jīng)編機(jī)故障預(yù)測框架

圖2所示為基于PCA與距離判別法的經(jīng)編機(jī)故障預(yù)測框架,對歷史樣本進(jìn)行主元分析,確定模型的主元及提取經(jīng)編機(jī)故障特征信息形成模型的訓(xùn)練集,并由此得到主成分分析-距離判別法經(jīng)編機(jī)故障預(yù)測模型[3]。對經(jīng)編機(jī)實(shí)時(shí)采集的數(shù)據(jù)進(jìn)行相應(yīng)的預(yù)處理,得到經(jīng)編機(jī)實(shí)時(shí)數(shù)據(jù)的特征信息,并將其輸入預(yù)測模型中完成經(jīng)編機(jī)故障預(yù)測。

使用主成分分析與距離判別法進(jìn)行經(jīng)編機(jī)故障預(yù)測的基本流程見圖3,整個(gè)流程圖由三部分組成,即經(jīng)編機(jī)故障預(yù)測模型的建立與利用經(jīng)編機(jī)故障預(yù)測模型進(jìn)行故障預(yù)測,其中數(shù)據(jù)預(yù)處理包括數(shù)據(jù)的整理和數(shù)據(jù)標(biāo)準(zhǔn)化處理兩部分。

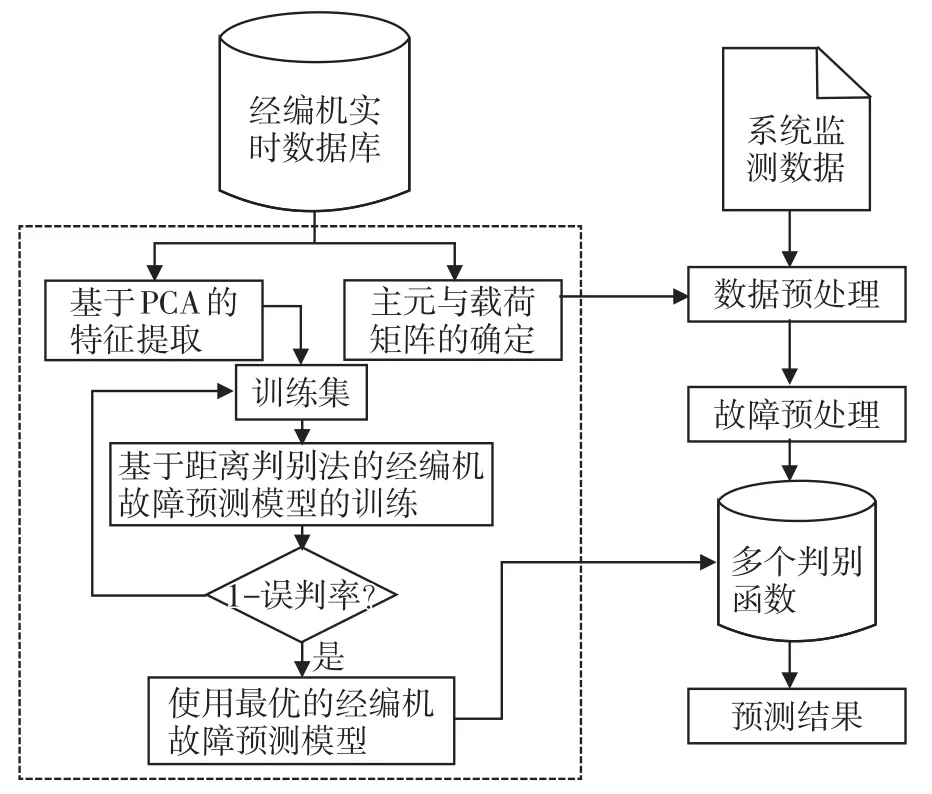
圖2 經(jīng)編機(jī)故障預(yù)測模型

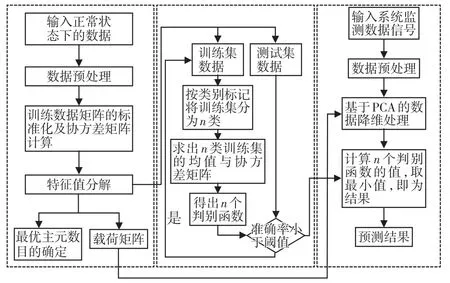
圖3 經(jīng)編機(jī)故障預(yù)測的基本流程圖

2.2 經(jīng)編機(jī)故障預(yù)測模型

2.2.1 數(shù)據(jù)預(yù)處理

本文結(jié)合本領(lǐng)域?qū)＜业闹R和經(jīng)編機(jī)生產(chǎn)歷史數(shù)據(jù)統(tǒng)計(jì)表,選取影響經(jīng)編機(jī)故障預(yù)測指標(biāo)中的8個(gè)特征參數(shù)作為條件屬性,分別為轉(zhuǎn)速、經(jīng)編機(jī)運(yùn)行情況、故障代碼、生產(chǎn)時(shí)間、停機(jī)次數(shù)、停機(jī)時(shí)間、維修次數(shù)、維修時(shí)間;采取經(jīng)編機(jī)運(yùn)行8個(gè)特征參數(shù)作為判別依據(jù),對各屬性值按連續(xù)數(shù)據(jù)和離散數(shù)據(jù)進(jìn)行如下劃分：

(1)連續(xù)數(shù)據(jù) 主要包括轉(zhuǎn)速、生產(chǎn)時(shí)間、停機(jī)時(shí)間、維修時(shí)間,這些連續(xù)數(shù)據(jù)都屬于連續(xù)值。為了更好地利用主成分分析理論對經(jīng)編機(jī)故障預(yù)測指標(biāo)進(jìn)行降維處理,必須對樣本空間中存在缺失值的樣本點(diǎn)進(jìn)行缺失值插入處理。為保持樣本空間原有的分布,本文采用的是均值插入方法。

(2)離散數(shù)據(jù) 主要包括經(jīng)編機(jī)運(yùn)行情況、故障代碼、停機(jī)次數(shù)等。對離散數(shù)據(jù)進(jìn)行缺失值處理時(shí)依然采用的是均值插入方法,但缺失值的替補(bǔ)值不再是平均值,而是用該樣本點(diǎn)所在的樣本空間中其他所有樣本點(diǎn)存在值的眾數(shù)來代替該缺失值。

2.2.2 主成分分析

主成分分析是經(jīng)編機(jī)故障預(yù)測模型中不可或缺的模型,因?yàn)樵谠紨?shù)據(jù)集中屬性與屬性之間可能存在相互關(guān)系,而這種相互關(guān)系會(huì)造成模型的預(yù)測效果不好,可能會(huì)產(chǎn)生過擬合現(xiàn)象。本文采用主成分分析進(jìn)行降維處理,其基本計(jì)算方法是：將訓(xùn)練樣本集進(jìn)行標(biāo)準(zhǔn)化處理,計(jì)算樣本空間樣本點(diǎn)的相關(guān)系數(shù)矩陣,求出相關(guān)系數(shù)矩陣的特征值及相應(yīng)的特征向量,然后計(jì)算主成分貢獻(xiàn)率及累計(jì)貢獻(xiàn)率,再計(jì)算主成分載荷,最后計(jì)算因子判別式[4]。

算法步驟如下：

(1)根據(jù)主成分分析原理將數(shù)據(jù)進(jìn)行標(biāo)準(zhǔn)化處理;

(2)根據(jù)算式求相關(guān)系數(shù)矩陣,并計(jì)算相關(guān)系數(shù)矩陣;

(3)選取主成分特征值越大相對應(yīng)的主成分?jǐn)?shù)據(jù)越重要,選取主成分?jǐn)?shù)據(jù)一般包含到85%以上即可,代表標(biāo)量的大部分原始信息[5];

(4)計(jì)算主成分載荷,它主要反映主成分與原變量的相互關(guān)聯(lián)程度;

(5)根據(jù)主成分載荷矩陣,計(jì)算因子判別式;

(6)輸出因子判別式。

2.2.3 距離判別法模型的建立

采用馬氏距離其基本方法是：首先計(jì)算各類樣本空間的均值,然后計(jì)算各個(gè)樣本空間的協(xié)方差矩陣,計(jì)算任意兩樣本空間的距離,求出線性判別函數(shù),實(shí)現(xiàn)預(yù)測功能。

算法步驟如下：

(1)根據(jù)距離判別法計(jì)算樣本均值;

(2)計(jì)算樣本的協(xié)方差矩陣;

(3)計(jì)算任意兩總體距離;

(4)根據(jù)計(jì)算的總體距離,得出線性判別公式。

2.2.4 故障預(yù)測模型驗(yàn)證

預(yù)測模型驗(yàn)證實(shí)質(zhì)上就是進(jìn)行模型有效性分析,是判斷建立的預(yù)測模型是否準(zhǔn)確代表實(shí)際系統(tǒng);一方面是確保采集的數(shù)據(jù)適用于建立的預(yù)測模型,另一方面是檢驗(yàn)?zāi)Ｐ洼敵鍪欠窠咏鼘?shí)際系統(tǒng)。判別結(jié)果的評價(jià)一般根據(jù)對原始數(shù)據(jù)、驗(yàn)證樣本的準(zhǔn)確預(yù)測來評價(jià)分類效果的好壞,對原樣本及訓(xùn)練樣本驗(yàn)證方法有組內(nèi)考核,組內(nèi)回代,對驗(yàn)證樣本的驗(yàn)證法有組外考核等。

本文所采用的驗(yàn)證方法如下：

(1)對于訓(xùn)練樣本,采用組內(nèi)回代法驗(yàn)證模型效果是否準(zhǔn)確,假設(shè)G1,G2…Gn為n個(gè)總體,分別抽取容量為n1,n2的樣品,設(shè)nmn表示實(shí)際歸類Gn,預(yù)測歸類Gm的樣本數(shù)。使用誤差率來估計(jì)誤判率,準(zhǔn)確率為1減估計(jì)誤判率,其算式為：

(2)對于驗(yàn)證樣本,將驗(yàn)證樣品代入預(yù)測模型,與實(shí)際結(jié)果進(jìn)行比較。

3 結(jié)語

通過分析影響經(jīng)編機(jī)故障預(yù)測的各類指標(biāo),采用基于主成成分分析對海量的經(jīng)編機(jī)生產(chǎn)狀態(tài)數(shù)據(jù)進(jìn)行降維處理,并構(gòu)建了基于距離判別法評估的故障預(yù)測模型,從而實(shí)現(xiàn)了經(jīng)編機(jī)的智能化故障預(yù)測。通過測試數(shù)據(jù)集進(jìn)行驗(yàn)證,結(jié)果顯示預(yù)測誤判率較低。